改进的小生境混合遗传算法在函数优化上的应用*

王 聪， 柯沪琦， 胡燕海

(1.宁波大学 机械工程与力学学院，浙江 宁波 315211；2.宁波戴维医疗器械股份有限公司，浙江 宁波 315712)

应用技术

改进的小生境混合遗传算法在函数优化上的应用*

王 聪1， 柯沪琦2， 胡燕海1

(1.宁波大学 机械工程与力学学院，浙江 宁波 315211；2.宁波戴维医疗器械股份有限公司，浙江 宁波 315712)

为了提高经典小生境遗传算法的收敛性能，加强局部寻优能力，设计了一种新的小生境混合遗传算法。通过判断算法的在线性能指标Xe(s)，将模拟退火算法巧妙地融入算法的后期，并针对小生境遗传算法的特点选用格雷码编码，同时设计了自适应的遗传交叉算子。用一个Shubert多峰值函数对改进的算法进行验证，结果表明:新算法的收敛性能和进化效率得到提高，局部寻优能力也有加强。

小生境； 混合遗传算法； 模拟退火算法； 在线性能指标

0 引 言

现今存在的一些优化算法，均具有各自的优点，但又存在或多或少的缺点。如：模拟退火法、爬山法局部寻优能力好，但全局寻优能力差；普通的遗传算法容易早熟，全局寻优能力好。因此，根据经验渐渐形成了混合遗传算法的概念，融合算法之间的优点，使求解问题更具效率，求解质量也得到提高[1～8]。

基于混合遗传算法的理念，出现了很多小生境实现技术。如文献[2]中提出了一种基于相似个体交叉和(μ+λ)确定性择优机制的小生境技术，能提高全局收敛可靠性，加快收敛速度。文献[3]中提出了一种基于小生境模拟退火的遗传算法，从过程上看，该方法在每一轮进化的末尾执行了模拟退火操作，实现方式比较机械，达不到最优化的混合遗传算法要求[4～7]；从效果上看，该方法依然只能提高收敛速度，没有解决局部寻优性能差的缺点。

本文提出了一种改进的小生境混合遗传算法，不但能在最适宜的点融入模拟退火算法，而且采用格雷码代替二进制编码，同时改进了遗传算子。最后，将该算法运用于优化一个具体函数，结果表明:算法能加快收敛速度，提高搜索效率，并有较强的局部寻优能力。

1 经典小生境遗传算法存在的问题

经典小生境遗传算法对两个在一定距离S之内的个体，比较其适应度大小，通过一个罚函数，淘汰适应度较小的个体，保留距离S内的优良个体。最终，群体不但具有较好的多样性，还能使个体之间分布均匀。但是小生境遗传算法也存在着局部寻优能力不强，容易陷入进化停滞的问题[9～20]。

另外，由于小生境遗传算法需要计算每两个个体之间的海明距离，并对适应度较低的个体处以罚函数，算法复杂，加大计算量，对于种群规模大的群体，计算效率难以保证。当群体进化到后期，优质个体的数量大大增加，或个体的目标函数值已进化到最优解附近，此时如果仍然采用经典小生境遗传算法，将增加计算负担[21～24]。

2 小生境混合遗传算法

为了提高小生境遗传算法的局部寻优能力和算法的计算效率。在经典算法中融入了局部寻优能力较强的模拟退火算法，并采用格雷码的编码方法，以及与编码方法相对应的自适应遗传算子。

2.1 模拟退火算法

模拟退火算法利用了退火这一金属热加工工艺原理, 随着温度的降低，物质的能量将逐渐趋近于一个较低的状态，并最终达到某种平衡。运用到函数优化中，能以随机搜索技术从概率的意义上找出目标函数的全局最小点。

算法描述如下：

1)设置一个初始点，计算得到目标函数值；

2)规定循环计数器初值：t=1；

3)设置初始温度：θ=T0；

4)使用变异操作于初始点，初始点变异后，计算得到目标函数值的Δ增量；

5)若Δ<0，则当前最优点就是新产生的最优点；若Δ≥0，则新产生的最优点将以p=e(-Δ/θ)的概率成为当前最优点；

6)如果t小于结束步数，则t=t+1，转向第(4)步；

7)如果未达到冷却状态，则θ=T(t)，转向第(2)步；如果达到冷却状态，则输出当前最优点，计算结束。

2.2 格雷码编码

格雷码是二进制编码的一种变形，主要有两个特点：1)两个连续的整数编码值不同之处只有一个码位；2)两个整数所代表的格雷码之间的海明距离刚好是这两个整数的差。特点(1)使算法的局部搜索能力得到提高，使交叉、变异操作易于实现。特点(2)在计算某两个点的海明距离时，只需计算对应的两个整数的差，可大大简化计算步骤，提高计算效率。

2.3 遗传选择算子

选用称为稳态复制的最优保存策略进化模型，以对已经过模拟退火操作的群体进行一次优胜劣汰操作。

2.4 自适应交叉算子

在进化过程的不同时期，群体中优质个体的数量不同，若自始至终使用同一概率对种群个体进行交叉操作，群体的优化程度得不到保证。比如，在进化早期，期望较大的交叉概率，使整个群体的优行能在短时间内完成；但是在进化的末期，种群中存在较多好的个体，为了避免破坏那些已优化的个体，则期望交叉概率较小。为此，设计了一种自适应交叉概率函数

(1)

式中 Pc为当前代数对应的交叉概率；Pn为常规交叉概率；t为当前进化代数；C为一个常数。

在实际操作过程中，在进化前期即进化代数t小于进化总代数T的60 %时，交叉概率固定。当进化代数t大于等于进化总代数T的60 %时，则根据式(1)确定每一代群体的交叉概率。

2.5 小生境操作

1)按式(2)计算种群规模为W的群体中任意两个个体Xi和Xj的海明距离

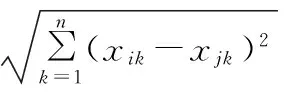
i=1,2,…，W-1,j=i+1,…，W

(2)

2)当个体Xi和Xj的海明距离小于L时，对个体Xi和Xj中适应度较低的个体施加一个罚函数Penalty。

3)对种群按适应度大小进行降序排列，保留排名在前n位的个体，组成新的群体。

3 混合遗传算法构成框架

在线性能指标(遗传算法性能的评价指标之一)指

(3)

式中fe(t)为在环境e下t时刻的平均目标函数值或平均适应度；s为算法策略。根据式(3)，在线性能指标的含义是遗传算法自开始一直到结束的一段时间内性能值的平均。

小生境遗传算法存在容易陷入进化停滞和局部最优性能差的缺陷，因此可利用在线性能指标来判断当前目标函数值是否已接近最优值，时可换用模拟退火算法这一类局部寻优能力强的优化算法，不但可以尽快找到全局最优值，而且能提高算法的效率，减少计算时间。详细见图1。

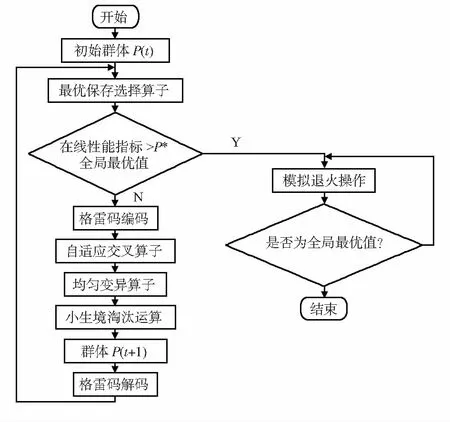
图1 改进的小生境遗传算法流程图

图1中的P(0

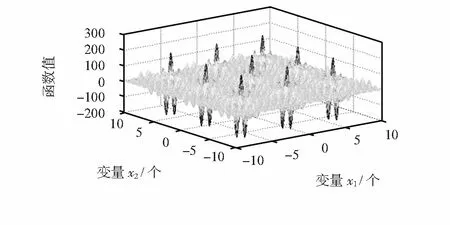
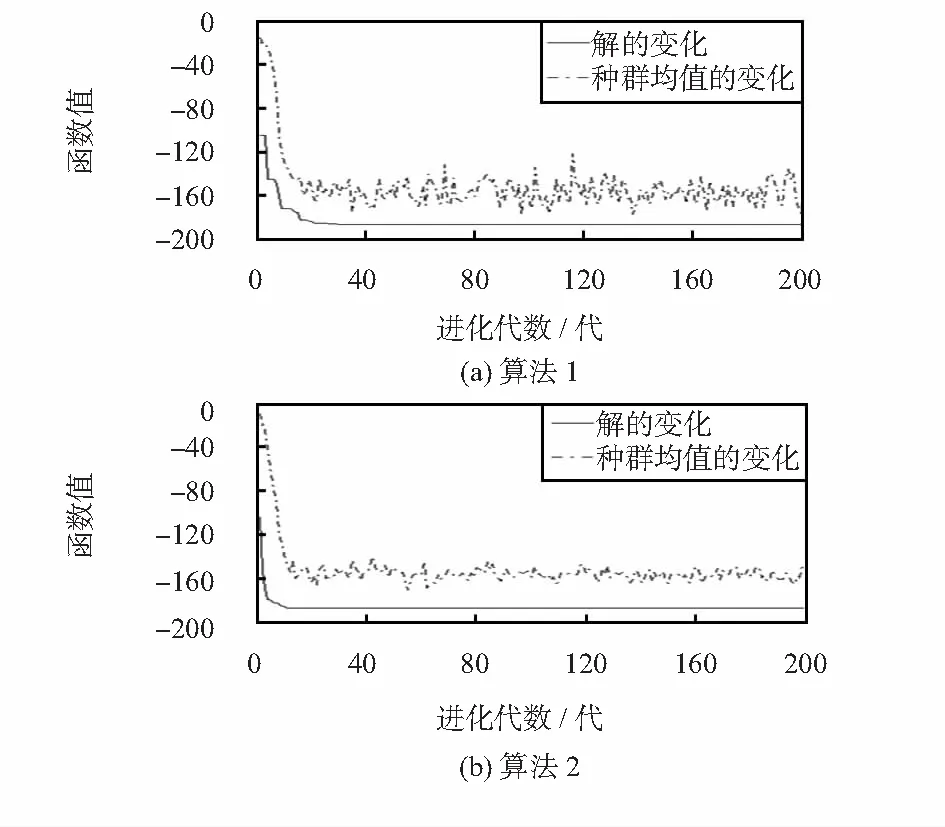
4 多峰值函数应用

为了测试经改进的小生境混合遗传算法的性能，本文选用了Shubert多峰值函数，并与经典小生境遗传算法对Shubert函数的优化结果进行了比较。

4.1Shubert函数

Shubert函数可描述为

(4)

这是一个二元多峰值函数，如图2所示，其定义域内共有760个局部最小点，其中18个点为全局最小点，全局最小值为f=-186.731。

用小生境遗传算法求解函数时，需用式(5)进行目标函数值到个体适应度的变换处理

(5)

图2 Shubert多峰值函数图像

4.2 参数设置

经典小生境遗传函数参数设定为：二进制编码串长度l=20×2(其中每个变量用10位二进制编码来表示);初始种群规模M=100;交叉概率PC=0.8;变异概率Pm=0.05;最大进化代数T=5000;小生境之间的距离参数L=0.5;罚函数Penalty=10～30。终止条件：算法进化代数为最大值500时，实验次数为50次。

改进的小生境混合遗传函数参数设置为：格雷码编码串长度l’=20×2(相同长度的格雷码与二进制编码串精度相同);初始种群规模M=100;自适应交叉概率P’C根据公式(1)得到;变异概率为P’m=0.05;小生境之间的距离参数L’=0.5;罚函数Penalty’=10～30;判断是否进入模拟退火算法的概率p=0.9。终止条件：小生境遗传算法和模拟退火算法的总进化代数为最大值500时，实验次数为50次。

4.3 实验结果

图3为两种算法各实验50次所绘制的平均进化图。算法1为经典小生境遗传算法，算法2为改进的小生境混合遗传算法。

由图3中“解的变化”曲线可知：算法1收敛到全局最优解大概需要进化25代左右，而算法2收敛到全局最优解只需进化10代左右的时间。可见，算法2的收敛速度得到了明显提高。由图中“种群均值的变化”曲线可知：使用算法2进化的种群，其均值变化幅度明显减小，可见，算法2的局部寻优能力也得到加强。

从运行到终止条件而停止时，算法1需要平均步数为281步，算法2需要平均步数为116步。可见，算法2的进化步数明显小于算法1，证明了当目标函数值达到最优值的90 %后，使用模拟退火算法寻优的确可以提高进化速度。

图3 两种算法进化结果比较

5 结 论

本文针对经典的小生境遗传算法存在容易陷入进化停滞和局部寻优性能差的缺陷，提出了一种改进的小生境混合遗传算法，对遗传算子改进的同时，引入模拟退火算法，并给出了算法流程框图。经实验证明，新算法能有效提高算法效率，加强局部寻优能力。

[1] 周 明，孙树栋.遗传算法原理及应用[M].北京:国防工业出版社，1999:70-79.

[2] 喻寿益，郭观七.一种改善遗传算法全局搜索性能的小生境技术[J].信息与控制，2001，30(6):526-530.

[3] 赵 敏，林道荣，瞿 波，等.一种新的基于小生境模拟退火的遗传算法[J].辽宁工程技术大学学报：自然科学版，2013，32(3):45-51.

[4] 宗德才，王康康.一种混合局部搜索算法的遗传算法求解旅行商问题[J].计算机应用与软件，2015(3):15-21.

[5] 王秋芬，梁道雷.一种求解0—1背包问题的启发式遗传算法[J].计算机应用与软件,2013(2):68-73.

[6] 屈志毅，文雪飞，范志明，等.基于遗传模拟退火算法的多约束QOS组播路由优化算法[J].计算机应用与软件，2007(12):44-49.

[7] 张志鹏，黄 明.基于改进多目标遗传算法求解混合流水车间调度问题[J].计算机应用与软件，2015(10):88-95.

[8] 姜封国.结构系统基于可靠性的优化设计研究[D].哈尔滨:哈尔滨工程大学，2009.

[9] 袁丽华.基于物种进化的遗传算法研究[D].南京:南京航空航天大学，2009.

[10] 杨晓华.参数优选算法研究及其在水文模型中的应用[D].南京:河海大学，2002.

[11] 刘 楠.改进的小生境遗传算法在多目标车间调度中的应用研究[D].大连:计算机应用技术，2010.

[12] 黄聪明，陈湘秀.小生境遗传算法的改进[J].北京理工大学学报，2004，6(8):46-52.

[13] 程绍清.自适应微型遗传算法在动态本构参数反演中的应用[D].长沙:湖南大学，2010.

[14] 邹腊梅，龚向坚，肖 芳，等.基于模拟退火算法与隐马尔可夫模型的Web信息抽取[J].南华大学学报，2011，10(1):151-156.

[15] 王友钊，彭宇翔，潘芬兰.基于贪心算法和遗传算法的仓储车辆调度算法[J].传感器与微系统，2012，31(10):88-93.

[16] 张荣祥，李正强，郑世杰.基于遗传算法的双阈值小波去噪方法研究[J].传感器与微系统，2007，26(6):46-52.

[17] 朱海燕，王力虎.基于遗传算法的合作演化仿真[J].传感器与微系统，2010，29(12):111-116.

[18] 汪 芸，涂启玉，陈 华.洪水演算中马斯京根法的新改进[J].人民长江，2008，24(2):36-41.

[19] 涂启玉.基于小生境遗传算法的区域水资源优化配置[J].水利科技与经济，2008，5(3):78-83.

[20] 李 兵.瑞雷波技术在巨粒土路基检测中的应用[D].重庆:重庆交通大学，2011.

[21] 虞安军.基于遗传算法的高速公路路面养护决策优化研究[D].长沙:长沙理工大学，2007.

[22] 周洪伟.遗传算法“早熟”现象和改进策略研究[D].郑州:解放军信息工程大学，2004.

[23] Zheng Q，Sha J，Shu J，et al.A variant constrained genetic algorithm for solving conditional nonlinear optimal perturbations[J].Advances in Atmospheric Sciences，2014，31(1):219-229.

[24] Ulas K，Kürsat A.Optimal power flow solution of two-terminal HVDC systems using genetic algorithm[J].Electrical Enginee-ring，2014，96(1):65-77.

王 聪(1992- )，男，硕士，研究方向为遗传算法，嵌入式工程。

胡燕海(1965- )，男，通讯作者，博士，教授，从事机电液产品开发，生产计划与控制领域研究工作，E—mail：373980986@qq.com。

Application of improved niche hybrid genetic algorithm in function optimization*

WANG Cong1， KE Hu-qi2, HU Yan-hai1

(1.Faculty of Mechanical Engineering and Mechanics,Ningbo University,Ningbo 315211,China;2.Ningbo David Medical Device Corporation,Ningbo 315712,China)

In order to improve the convergence of classical niche genetic algorithm,strengthen local optimizing ability,a new niche hybrid genetic algorithm is designed.By judging online performance indicatorsXe(s)of algorithm, the simulated annealing algorithm is cleverly fused into later algorithm, and aiming at characteristics of the niche genetic algorithm,choose Gray code coding,at the same time,adaptive genetic crossover operator is designed.Using a Shubert multimodal function to validate the improved algorithm,the results show that the convergence of the new algorithm and evolutionary efficiency is improved,the local optimization ability is also strengthened.

niche； hybrid genetic algorithm； simulated annealing algorithm； online performance indicators

10.13873/J.1000—9787(2017)05—0153—04

2016—07—21

国家自然科学基金资助项目(51408323)； 宁波市重大科技专项资助项目(2015C110033)

TP 18

A

1000—9787(2017)05—0153—04