题在书外根在书内
何勇
题在书外根在书内
何勇
数学课本中的例题具有示范性、典型性和探究性,是课本的精髓.浏览近几年全国各地的中考数学试卷,很多试题来源于课本,“题在书外,根在书内”.因此,我们在平常学习过程中如果能充分重视和挖掘课本中例题的潜在功能,适当加以拓展延伸,可以达到事半功倍的效果.
原题(苏科版《数学》九下第72页例2)如图1,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G,设DE=6,BC=10,GF=5,求点A到DE、BC的距离.
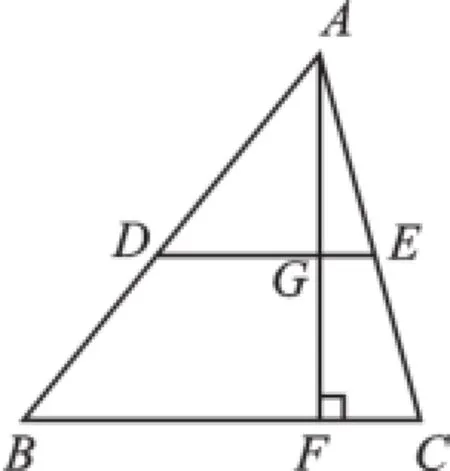
图1
【思路点拨】由DE∥BC,易得△ADE∽△ABC,利用相似三角形对应高之比等于相似比易求出AG=7.5,AF=12.5.
变式1如图2,正方形ABCD是一块绿化带,其中阴影部分EOFB、GHMN都是正方形的花圃.已知自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为().
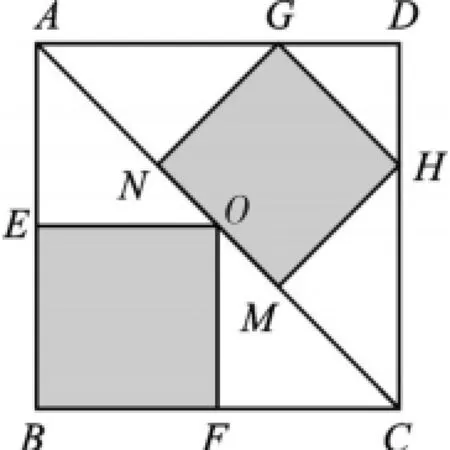
图2
【思路点拨】求得阴影部分的面积与正方形ABCD的面积的比即可求得小鸟落在花圃上的概率.
【简解】设正方形ABCD的边长为a,
变式2如图3,有一块三角形的余料ABC,要把它加工成矩形的零件,已知:BC= 8cm,高AD=12cm,矩形EFGH的边EF在BC边上,G、H分别在AC、AB上,设HE的长为ycm,EF的长为xcm.
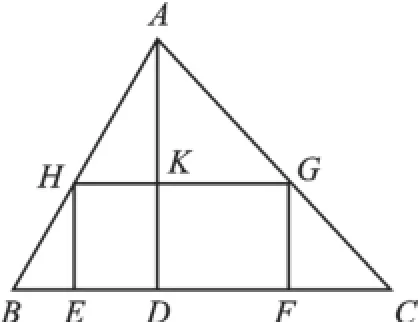
图3
(1)写出y与x的函数关系式.
(2)当x取多少时,矩形EFGH是正方形?
【思路点拨】(1)先由BC=8cm,高AD=12cm,HE的长为ycm、EF的长为xcm,可知,AK=(12-y)cm,HG=EF=xcm,再根据HG∥BC可知△AHG∽△ABC,由相似三角形的对应边成比例即可得出y与x的函数关系式;
(2)根据正方形的性质可知y=x,再代入(1)中所求的代数式即可得出结论.
【简解】(1)由HG∥BC,所以△AHG∽△ABC,所以
【说明】本题难点是将相似的性质和一次函数相结合,根据相似三角形对应高的比等于相似比,找出相似三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
变式3一块三角形废料如图4所示,∠A=30°,∠C=90°,AB=12.用这块废料剪出一个矩形CDEF,其中,点D、E、F分别在AC、AB、BC上.要使剪出的矩形CDEF面积最大,点E应选在何处?
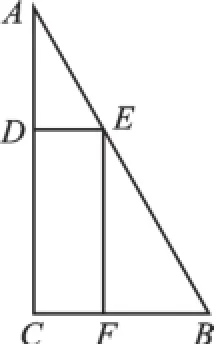
图4
【思路点拨】首先在Rt△ABC中利用∠A= 30°、AB=12,求得BC、AC的长,然后根据四边形CDEF是矩形得到EF∥AC,从而得到△BEF∽△BAC,设AE=x,则BE=12-x.利用相似三角形成比例表示出EF、DE,然后表示出有关x的二次函数,最后求二次函数的最值即可.
【简解】在Rt△ABC中,∠A=30°,AB=12,所以BC=6,AC=6 3.由△BEF∽△BAC得:x).在Rt△ADE中矩形CDEF的面积S=DE·当x=6时,S有最大值.所以点E应选在AB的中点处.
【说明】本题难点在于利用相似三角形的性质得到矩形CDEF面积表达式,解题的关键是从几何问题中整理出二次函数模型,并利用二次函数的知识求最值,从而确定点E的位置.
变式4如图5(1),△ABC是一张等腰直角三角形彩色纸,AC=BC=50cm.将斜边上的高CD五等分,然后裁出4张宽度相等的长方形纸条.若用这4张纸条为一幅正方形美术作品镶边(纸条不重叠),如图5(2),则正方形美术作品最大面积是cm2.
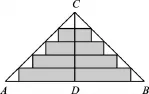
图5 (1)

图5 (2)
【思路点拨】利用相似三角形的性质求出每个纸条的长,将其相加,易得纸条的总长度,计算出正方形的边长,从而计算面积即可.
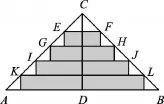
图6
【说明】此题考查了相似三角形的应用,难点在于不仅要计算出纸条的长度,还要计算出宽度,要仔细观察图形,寻找相似三角形,并利用相似三角形对应高的比等于相似比,来获得等量关系,从而解决.
(作者单位:江苏省无锡市太湖格致中学)

