理知识脉络抓重点难点看问题本质
姜鸿雁
理知识脉络抓重点难点看问题本质
姜鸿雁
一、关注图形变化前后的“对应”
无论哪类图形变换,关注图形变化前后的对应关系是关键,关注对应点、对应角、对应边,则便于发现平移的距离、旋转的角度、对称轴或比例线段等关于图形变换的重要“指标”,也便于运用各类图形变换的性质,使问题迎刃而解.
例1(2016·新疆)如图1,将一个含30°角的直角三角板ABC绕点A旋转,使得点B、A、C′在同一条直线上,则三角板ABC旋转的角度是().
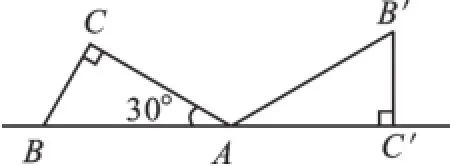
图1
A.60°B.90°C.120°D.150°
【解析】C、C′是对应点,AC、AC′是对应边,因为对应边夹角是旋转角,所以∠CAC′是旋转角,所以本题选D.
例2(2016·泰州)如图2,在△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为cm.
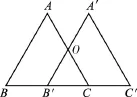
图2
【解析】图形平移的距离是指对应点之间的距离,即BB′或CC′的长,由平移的性质知对应边平行,易得△OB′C∽△ABC,因为O为AC中点,所以相似比为,则B′C=2.5(cm),所以BB′=2.5(cm).
二、关注图形变化中整体与部分的关系
无论哪类图形变换,部分与整体之间都存在着依存关系:图形上每个点随着图形整体做相同方式运动.
例3(2016·青岛)如图3,线段AB经过平移得到线段A′B′,其中点A、B的对应点分别为A′、B′,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为().
A.(a-2,b+3)B.(a-2,b-3)C.(a+2,b+3)D.(a+2,b-3)
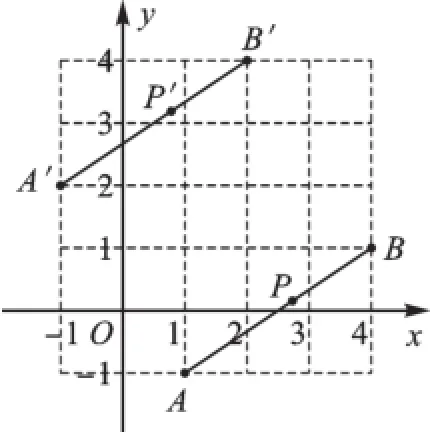
图3
【解析】因为在运动过程中,图形上所有的点都按相同的变化规律运动,虽然点P不是格点,但可以从线段端点A或B(它们是格点)容易发现变化规律是:向左平移2个单位,向上平移3个单位,所以答案为A.
三、关注坐标中“藏”着的“秘密”
当图形放置在平面直角坐标系下,坐标可以确定图形的位置,图形的运动方式也可以通过坐标的方式来体现,善于发现坐标中的“秘密”,是我们发现问题本质的一条重要途径.
例4(2016·滨州)正五边ABCDE放入某平面直角坐标系后,若顶点A、B、C、D的坐标分别是(0,a)、(-3,2)、(b,m)、(c,m),则点E的坐标为().
A.(2,-3)B.(2,3)
C.(3,2)D.(3,-2)
【解析】正五边形是轴对称图形,由A点坐标可知它在y轴上,C、D两点的坐标“告诉”我们CD平行于x轴,所以本题的本质就是求B点关于y轴的对称点E的坐标,故选C.
例5(2016·河南)如图4,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为().
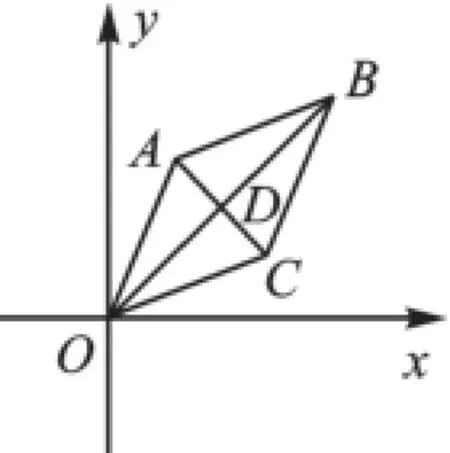
图4
【解析】点B坐标(2,2)“藏”着OB与x轴夹角是45°,每秒旋转45°,则意味着每8秒,点B回到原处,60秒时,点B旋转到第三象限,而菱形绕O点旋转时,点B、对角线交点D也同样随整体一起旋转,所以此时点D的坐标是(-1,-1).
四、图形的变化是重要思想方法与策略
图形的变化不仅是一个个具体的知识,也是我们解决问题的重要思想方法与策略,巧妙运用图形变化思想,有助于我们发现问题的本质,绕开易错的烦恼,达到事半功倍的效果.
例6(2016·淄博)如图5是由边长相同的小正方形组成的网格,A、B、P、Q四点均在正方形网格的格点上,线段AB、PQ相交于点M,则图中∠QMB的正切值为.
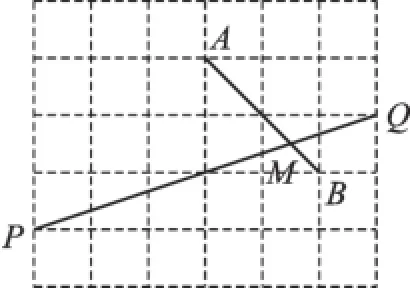
图5
【解析】在网格问题中,应该关注格点,也“希望”要求的目标与格点相关,将线段AB上移一格再右移一格,使B、Q重合(如图6),由平移性质得∠QMB=∠FQP,且△FQP是直角三角形,所以tan∠QMB=tan∠FQP=2.
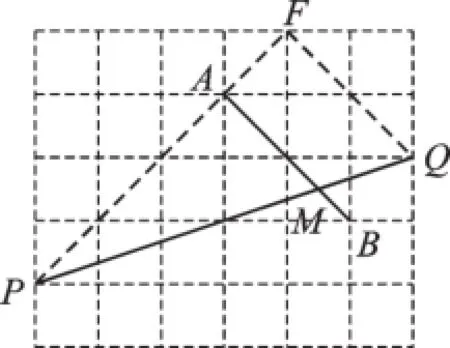
图6
例7(2015·娄底)一块三角板ABC按如图7所示的方式放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则B点的坐标为.
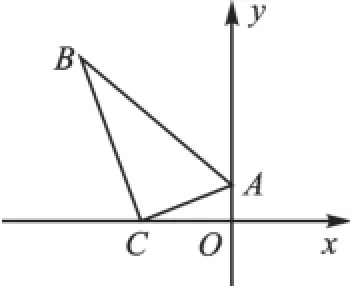
图7
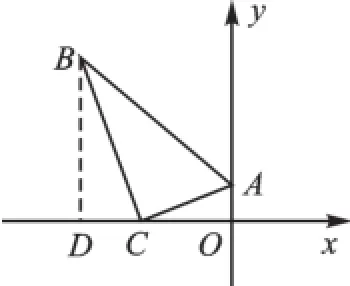
图8
【解析】过B点作BD⊥x轴于D,由相似变换可知△OCA∽△DBC,又因为在Rt△ABC中,∠B=30°,所以两个三角形的相似比为1∶,则DC=,DB=3.在求B点坐标时,我们可以这样思考:B点是由C点向左平移再向上平移33个单位得到的,则B点的坐标为(-3-3,33).用动态的思想求点的坐标,可以免去线段的长与坐标符号的正负性导致的错误.
结束语:图形的变化既体现在位置关系的变化上也体现在数量关系的变化上,可以单一变化,也可以组合变化,可以从知识认识它们,更要从解决问题的方法和策略上去认识它们,它们在呼唤我们要善于用动态的眼光去看待一个静态的图形,用这种独特的方式可以提升我们的思维能力.
(作者单位:江苏省无锡市河埒中学)

