“折纸”验证平行四边形——兼谈基本活动经验总结

徐小建

（江苏省南通市通州区平潮实验初级中学）

“折纸”验证平行四边形
——兼谈基本活动经验总结

徐小建

（江苏省南通市通州区平潮实验初级中学）

基本活动经验是《义务教育数学课程标准（2011年版）》所提出来的新概念，通过数学实验引导学生积累基本活动经验是数学教学的有效方法.通过“折纸”验证平行四边形的实验，概括出基本活动经验总结的以下方法：活动之前忆概念；理清本质方向明；揭示本质思路新；适时总结打基础；隐含条件是关键；融通本质有主见；话中有话激疑见；彻悟之后有创见；系统梳理再提炼.

折纸；平行四边形；基本活动经验

“折纸”是数学教学中最便捷的实验方法，本文通过“折纸”验证平行四边形教学活动来谈谈基本活动经验的总结.

一、教学实录及要点揭示

1.“折纸”验证正方形

问题情境：小红和小丽一起去商场买一条正方形的丝巾，她们各选中了一条，可是她们无法判断丝巾是否是正方形的.于是售货员A，拿起小红选的丝巾，如图1所示对折了两次，每次都能完全重合，于是售货员A对小红说：放心吧，丝巾肯定是正方形的！售货员B拿起小丽选的丝巾，如图2所示也对折了两次，每次也都能完全重合，于是售货员B对小丽说：放心吧，丝巾肯定是正方形的！小红、小丽对售货员的说法将信将疑.

（1）试给小红、小丽判断一下，丝巾一定是正方形的吗？

（2）如果你觉得售货员的方法不能判定丝巾是正方形的，试为她们想出一个用折叠进行判定的方法.

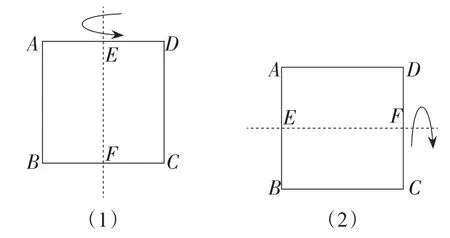
图1

图2

2.个人折纸模拟，小组交流

略.

3.全班交流共享

（1）为什么不能判定丝巾是正方形？

生1：图1和图2都不能说明丝巾是正方形的.

师：为什么？

生1：图1与图2的做法只能说明这块丝巾是轴对称图形，而轴对称图形不一定是正方形，所以……

师：其他同学有不同看法吗？

生2：图1和图2不能说明丝巾是正方形，但是生1的理由不成立，轴对称图形不一定是正方形，但是也不一定不是正方形.

师：那你说一说你的理由.

生2：我们小组也没想好，只是觉得这样的做法不能判定.

生2：菱形加直角，矩形加邻边相等，平行四边形加直角和邻边相等……

要点提示：数学实验的目的大致有两种：一种是探索型实验，用来启发思维、发现新知；另一种是验证性实验，用来验证事实、巩固新知.本节课的目的主要是后者.笔者的意图是通过白纸活动加深学生对平行四边形的性质、判定的理解，形成较为系统的认识.所以，当学生的思维受阻时，笔者引导学生从判定入手，理清思路.所以说，“活动之前忆概念”让学生活动在相关理论知识的指导下进行，提高活动的效率，避免盲目性是值得注意的问题.

师：看来生2是知道正方形的判定方法的，那么你再想想图1和图2的折叠能提供哪些判定的条件呢？

生2：图1的折叠重合能说明四边形的两组对边相等.

师：只有两组对边相等吗？

生2：还能说明四个角都相等.

师：确认吗？

Characteristics of Southern Indian Ocean Dipole variation and its relationship with ENSO events

生2：确认，因为第一次折叠重合说明∠A=∠D，∠B=∠C，第二次折叠重合说明∠A=∠B，∠D=∠C，所以∠A=∠D=∠B=∠C.

师：所以售货员A的折叠能说明四边形是……

生2：是矩形.

师：说得好，那么售货员B的折叠能说明四边形是……

生：能说明四边形是菱形.

要点提示：“理清本质方向明”，有了前面的理论回顾，学生明白了实验活动中所蕴含的数学本质，很快生2就从操作活动中提取出了有效的数学信息，判定了两种活动均不能判定丝巾为正方形.因此，在验证图形实验过程中，一定要让学生主动想明白，我们需要什么？我们验证了什么？然后在两者的对比中，我们就能发现实验是否达到预期目标.

（2）如何判定丝巾是正方形的？

师：好，刚才通过交流我们发现售货员A，B的做法都不能判定丝巾是正方形的，那么谁能帮小红、小丽确认一下丝巾到底是不是正方形的？

生3：只要将两种折叠方式都折一下，如果都能重合就说明丝巾是正方形的了.

师：为什么？

生3：如果两种折叠都能完全重合就说明四边形既是矩形又是菱形，那就一定是正方形.

师：说得对，那你再想想可不可以少折叠几次？

生3：可以的，只要折叠3次就可以了.

师：说得对，能再少吗？

……

师：我们请大家看一看图1和图2，或者你也可以用手中的纸片折叠，然后再想想最少折叠几次可以判定四边形是正方形.

生3：只要折叠两次就可以了.

师：怎么折？为什么？

生3：像图3（1）一样折叠一次，再像图3（2）一样折叠一次，如果两次都能重合就能说明四边形是正方形.

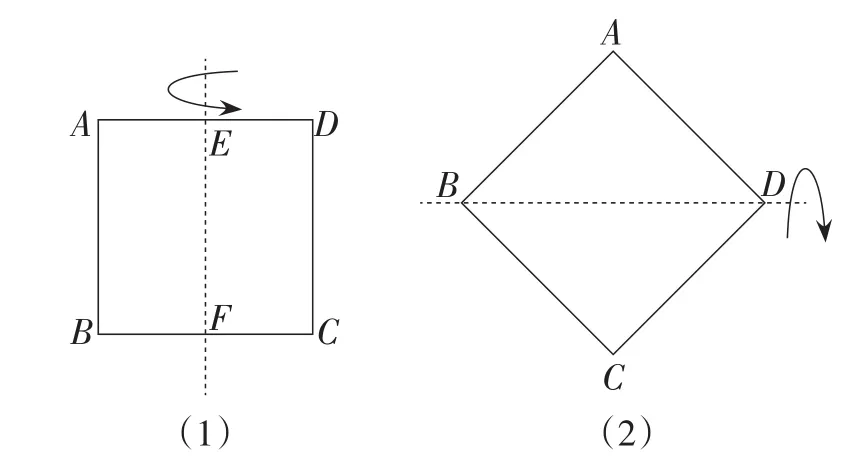
图3

师：能说说理由吗？

生3：第一次折叠能说明∠A=∠D，∠B=∠C，第二次折叠能说明∠A=∠C，AB=BC，这样就能证明四个角相等，且有一组邻边相等，那么它就既是一个矩形又有一组邻边相等，所以它就是一个正方形了.

师：还能通过其他方法说明吗？

生4：第一次折叠能说明AB=CD，∠A=∠D，第二次折叠能说明AB=BC，AD=DC，这样就能证明四条边相等，且有一组邻角相等，那么就可以证明它既是一个菱形又有一个直角，所以它就是一个正方形了.

要点揭示：“揭示本质思路新”，在理清了“我们需要什么？”之后进一步弄明白“我们能做什么？”这就揭示了问题的本质所在，有了这一层理解，学生很快找到了验证的方法，并且拾级而上经历了从繁到简的提升过程，从表面上看这是几种操作的简单组合，实质对学生来说也是一次有价值的创新.

（3）初步总结折纸经验.

师：通过刚才的交流，我们帮小红和小丽解决了丝巾是不是正方形的问题，现在我们来思考一下，在刚才的折纸活动中，我们判定了哪些四边形？

生4：我们判定了一个四边形是不是矩形、菱形和正方形.

师：能说具体一点吗？

生4：图1的两次对折都重合能说明四个角都相等，所以可以判定这个四边形是矩形；图2的两次对折都能重合说明四条边都相等，所以可以判定这个四边形是菱形；图3的两次折叠都能重合说明四条边相等，四个角也相等，所以可以判定这个四边形是正方形.

师：说得很好，下面我们再来思考这样的问题，图1中的一次对折完全重合能得出图形的哪些性质呢？

生5：能得出∠A=∠D，∠B=∠C，AB=CD.

师：说得对，这些性质都是我们通过折叠可以直接看出来的，再想想还有没有什么性质？

生6：AE=ED，BF=FC.

师：再看看，还有吗？

生7：∠AEF=∠FED.

师：等于……

生7：∠AEF=∠FED=90°，∠BFE=∠EFC=90°.

要点揭示：“适时总结打基础”，我们进行数学实验的目的应该有二：一是从教学角度让学生收获知识和能力；二是从教育角度让学生形成一定的活动经验.因此，适时的总结是形成基本活动经验的基础.在具体的问题解决之后，我们的思考还没有结束，一定要引领学生从活动中提炼出相关活动经验.在本片断中，笔者带领学生对由折叠所产生的性质进行了梳理，防止学生浅尝辄止，就事论事.在笔者的追问之下，学生对由折叠所产生的显性条件几乎是一网打尽，这种追问有利于学生形成全面分析问题的习惯.

师：你又发现什么性质了？

生7：哦，AD∥BC.

师：为什么？

生7：用同旁内角互补（∠AEF+∠BFE=180°），或内错角相等（∠AEF=∠EFC）都可以证明AD∥BC.

师：说得好！现在我们再来想想，在折纸的过程中，由折叠重合我们容易看得见的是线段的相等，角的相等，哪种关系我们不容易发现？

生7：线段的位置关系.

师：说得对，在刚才的一次对折重合之中，一开始我们就没能发现AD∥BC这样一种位置关系.下面请哪位同学来说明为什么这样的折叠方式能判定两线段平行？

生8：因为折痕和线段AD，BC形成了三线八角的图形，然后我们就可以判定AD∥BC.

师：等一下，老师有个疑问，是不是随意折一下，就能判定（折出图4）？

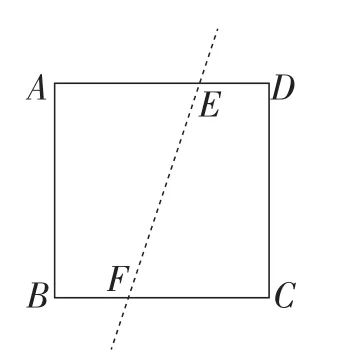
图4

生8：不能随意折，这样不能判定内错角相等或同旁内角互补.

师：那我们要怎样折？

生8：我们要将点A折到点D才行（折出图5）.

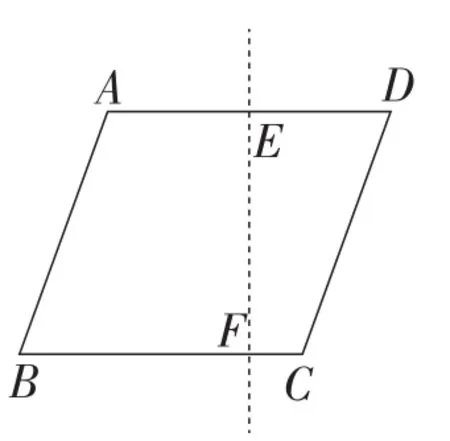
图5

师：为什么这样才行？

生8：这样折出折痕是线段AD的中垂线，这时候我们可以直接判定∠AEF=∠FED=90°.

师：说得好，也就是要使这条边折叠后与自身重合，这样我们就可以通过对折一组对边，看它们是否能同时与自身重合来判断这组对边是否平行.

要点揭示：“隐含条件是关键”，在引导学生适时总结的时候不仅要观察显性的表面的条件，更要引导学生分析由表面条件所产生的条件——“隐性条件”，这些条件往往是解决问题的关键.需要指出的是“引导学生学会发现隐含条件”也应成为通过操作实验培养学生观察能力、思维能力甚至创新能力的关键.在本片断中，教师步步紧逼，引导学生一步步地揭开了折叠重合中的隐含性条件，那就是同旁内角互补或内错角相等，从而判定一组对边平行.这一发现是令人惊喜的，在下面的片断中将会看到它的作用.

（4）验证任意平行四边形.

师：好，同学们，通过刚才的实验与交流，我们学会了通过折叠的方法验证菱形、矩形、正方形.下面我们来思考一下，能否设计一个折叠实验来验证任意平行四边形？

先个人实验，后小组交流，最后集中展示.

生9：我们可以通过这样的两次折叠来验证一个四边形是不是平行四边形.如图5，将线段AD折叠，使点A与点D重合，如果线段BC也能重合，这时由刚才发现的隐含条件就可以证明AD∥BC，同样可以验证AB∥DC，如图6所示.

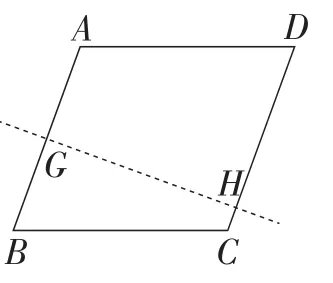
图6

师：“BC也能重合”是什么意思？

生9：是指线段BF与线段FC部分重合，当AE与ED完全重合时，BF与FC是不可能完全重合的，其实也不需要完全重合，只要部分重合就能说明折痕EF⊥BC了.

师：那么我们在折叠时一定需要AE与ED完全重合吗？

生9：也不一定，其实只要让AE与ED部分重合时，也能保证BF与FC部分重合，就说明折痕EF⊥AD，EF⊥BC，就能说明AD∥BC了.

师：说得好呀，做法可行，论证严谨，对于生9所演示的这个平行四边形，这种方法确实是可行的，大家明白了吗？

生：明白了！

要点揭示：“融通本质有主见”，学生在理解对折一边会产生“三线八角”的隐含条件之后很快就有了自己的发现，那就是并不需要将边对折，只要部分重合就能产生垂直于边的折痕，也就能产生可判定角相等（或互补）的三线八角，可以说一旦融通了本质，学生的创造性思维就立即被激发出来了，在探究过程中就会有更多自己的思考，而不是总去机械模仿了.这在下面的探究中更能得到体现.

师：生10，刚才大家都说明白了，那你说说你明白什么了？

生10：我明白了如何验证一个四边形是不是平行四边形.

师：如何验证？

生10：就用生9刚才的方法，分两次验证，一次验证一组对边是否平行.

师：是任意四边形吗？

生10：是的.

师：我把我刚才说的话再重复一下：说得好呀，做法可行，论证严谨，对于生9所演示的这个平行四边形，这种方法确实是可行了，大家明白了吗？

生10：难道说有的四边形用这种方法不可以验证？

师：下面，我们每位同学都动动手，看生9的方法是不是可以用来验证任意四边形是不是平行四边形？

生11：老师，确实有的四边形用生9的方法无法判定.如图7（1），我们用生9的方法可以判定AB∥DC，却不能验证AD∥BC，因为折痕不能同时和两条边都相交，如图7（2）.

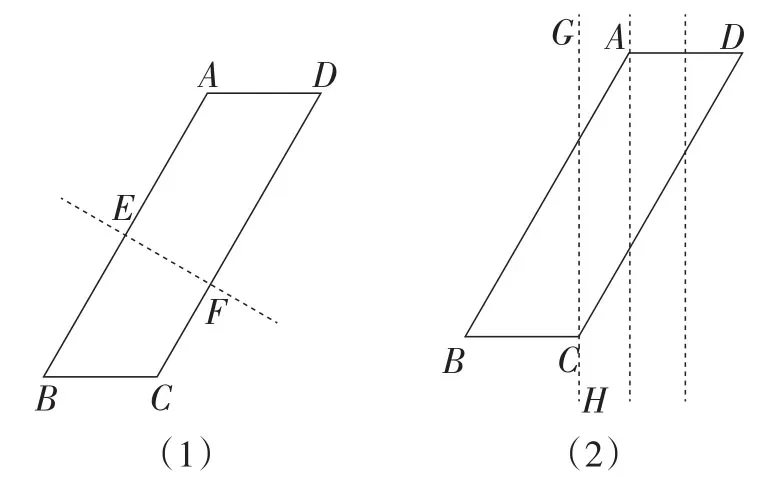
图7

师：说得非常好，刚才的验证为什么能进行呢？是因为我们利用了折痕，把它当作截线，构成了三线八角的图形，如图7（1）所示.而在图7（2）中，三线八角图形不存在了，所以我们没办法判定AD∥BC.那我们怎么办呢？

要点揭示：“话中有话激疑见”，当学生对事物的认识达到一定高度之后，会产生以偏概全、自以为是的感觉.一方面，是自信的表现；另一方面，也是思维不缜密的后果.因此，在教学的过程中教师不宜过度打击学生的积极性，也不宜助长学生自高自大的习气，这时候如果教师能通过适当的语言让学生听出弦外之音，从而冷静思考不失为好的办法.同时，这一做法还能在教师自己也拿不准时，在引导学生思考的同时为自己赢得思考的时间，不失为一种有效教学机智的表现.

个人思考、操作两分钟后小组交流两分钟.

生12：我们小组的方法是：①折对角线AC；②展平后折对角线BD；③展平后将点A折到点C，得折痕EF；④展平后将点B折到点D，得折痕GH.如图8，如果AC，BD，EF，GH都交于同一点，说明四边形是平行四边形.

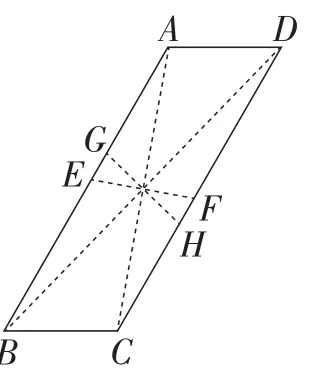
图8

师：能说说理由吗？

生12：我们这样做是验证两条对角线是否互相平分，如果AC，BD，EF，GH都交于同一点就说明两条对角线是互相平分的，四边形就是平行四边形，否则就不是.

师：我们其他各小组如果没想到这种验证方法的可以重复一下生12的折叠过程，体验并理解一下这种方法.然后我们再看看还有没有其他的方法？

生13：我们小组是这样验证的，先将平行四边形沿对角线AC折叠成图9（1）；再将点A折向点C，如果两侧的图形能完全重合，如图9（2）所示，则说明四边形是平行四边形，否则就不是平行四边形.

图9

师：能说说理由吗？

生13：我们暂时还没想好，只是觉得这样应该是.

师：哦，看来这个验证方法还有待论证.我们大家都拿出手中的四边形，按生13的方法进行折叠，先从直觉上来判断一下这种方法可行吗？

生：应该是可行的.

师：好，那我们就来共同攻关.请各小组来说明这种验证方法的合理性，然后交流.

生14：我们小组觉得可以这样说明，由图9（2）两侧完全重合，能说明AD=BC，OA=OC，OB=OD，然后由OA+OB=OC+OD，得AB=CD，这样由两组对边分别相等可以判定其为平行四边形.

师：说得好，还有其他说明方法吗？

生15：我们小组觉得可以这样说明，由图9（2）两侧完全重合，能说明∠OAC=∠OCA，∠D′=∠B，也就是展开图中的∠BAC=∠DCA，∠D=∠B，这样我们就容易得到一组对边平行，且有一组对角相等，而这个条件是可以证明四边形是平行四边形的.

要点揭示：“彻悟之后有创见”学生在经历了上述探究过程之后，对验证平行四边形的方法与原理有了较为彻底的认识，可以说是达到了“彻悟”的境界，这时的学生对知识、方法的调用可以说是应对自如.如果说图8的验证方法就是由判定直接推理的理性思维的结果的话，那么图9的方法可以说是彻悟之后的直觉流露.课后笔者问学生为什么会想到这么折，学生的回答是：就这样折了，也不知道为什么会想到这么折的.这其实就是多次探究经验积淀之后的一种厚积薄发.此外，学生（尤其是生14）对这一折法的说明的简洁程度也超出了教师的预期，这说明学生对折叠验证平行四边形的认识有了质的飞跃，达到有策略、有方法，甚至是有创见的程度.

师：说得非常好，看来高手在民间啊！那么还有其他不同的说明方法吗？

学生沉默.

师：那我们还有其他验证平行四边形的方法吗？

学生仍旧沉默.

师：好，那我们对折叠验证平行四边形的方法的研究就暂时告于段落，下面请哪位同学对本节课的学习过程做个小结.

（5）课堂小结.

生16：刚才我们用了三种方法验证了平行四边形，第一种方法如图5、图6所示，我们验证了两组对边分别平行；第二种方法是如图8所示，我们验证了对角线互相平分；第三种方法如图9所示，我们可以验证两组对边分别相等或一组对边平行，一组对角相等.

师：请你再思考一下，这三种方法是对任意的四边形都适用吗？

生16：第一种方法有时不可用，如图7、图8、图9所示，当折痕不能和一组对边中的每一条边都相交时第一种方法不可用.第二种方法、第三种方法是对每一个平行四边形都适用的.

师：请大家再思考一下，我们验证一个四边形是不是平行四边形最少要折几次？菱形呢？矩形呢？正方形呢？

生：两次.

师：下面我们再总结一下在今天的折叠活动中，你形成了哪些有关折叠的经验？

生17：可以折直线（线段），可以折垂线，直角.

生18：可以折一个角的平分线，还可以折平行线.

生19：可以折相等的线段，相等的角.

生20：还要重视利用折叠所推出来的条件，也就是“隐性条件”.

师：大家说得都非常好，其实关于折纸还有很多可以研究的内容，每个人都可以总结属于自己的经验，请同学们课后继续研究，你一定还会有新的发现.例如，发现新的验证方法，或者对某个验证方法发现新的说明方法.

要点揭示：“系统梳理再提炼”，当本节课的教学任务完成之后，引导学生再次进行自主梳理，其目的已经超出了具体的问题解决，而是要通过再次梳理、提炼形成一般性的策略，形成一定的思想方法，形成关于经验的积累.当然对数学思想方法的总结提炼不是一两节课就能解决的，但是只要我们坚持不懈地努力，每堂课都这么做，那么就一定会有效果.

二、结束语

基本活动经验是新一轮课程改革所提出来的新概念，本节课通过“折纸验证平行四边形”这一课题概括出“活动之前忆概念，理清本质方向明，揭示本质思路新，适时总结打基础，隐含条件是关键，融通本质有主见，话中有话激疑见，彻悟之后有创见，系统梳理再提炼”等方法，只是笔者在教学过程中的尝试，未必准确、全面，也未必在某一节课上全用得上.仅以此文引起一线教师对“基本活动经验总结”的关注.

［1］徐小建，李庾南.浅谈中学数学学程总结技艺：兼谈以时间为序的学程总结［J］.中国数学教育（初中版），2013（10）：8-10.

［2］余兴珍，缴志清.“特殊平行四边形性质与判定的综合运用”的学案设计与教学反思［J］.中国数学教育（初中版），2012（1/2）：8－11.

［3］沈岳夫.以“本”为源巧建模 提炼规律妙解题：对一类函数视角下平行四边形顶点坐标求解的研究［J］.中国数学教育（初中版），2014（11）：43-47，64.

2017—02—09

江苏省“十二五”规划重点资助课题——中学数学学程总结技艺研究（B-a/2013/02/004）．

徐小建（1970—），男，中学高级教师，主要从事初中数学教育、教学研究.