水驱气藏残余气饱和度实验与理论预测模型研究
罗 强 孙 雷 潘 毅 王 琼
(西南石油大学油气藏地质及开发工程国家重点实验室, 成都 610500)
水驱气藏残余气饱和度实验与理论预测模型研究
罗 强 孙 雷 潘 毅 王 琼
(西南石油大学油气藏地质及开发工程国家重点实验室, 成都 610500)
综合分析国内外残余气饱和度试验方法、影响因素、理论模型,发现初始含气饱和度与残余气饱和度的关联度较高。根据各项实验数据,确定初始含气饱和度在小于0.6时,对残余气饱和度的影响占主导地位。结合渗透率、孔隙度对残余气饱和度的影响,给出了多种因素影响下的残余气饱和度理论计算模型。
初始含气饱和度;孔隙度;渗透率
通常,稳态驱替法和非稳态驱替法测试均在高温高压下进行。高温高压下的实验条件符合地层条件,测试数据相对准确[1-2]。自发渗吸实验中,所测残余气饱和度偏高,不同的饱和历史和岩心清洗会影响到测试结果;而被动渗吸法中,随着流体流动速率的增加,残余气饱和度与驱替速率反相关[3-5]。初始含气饱和度越大,岩石胶结程度越高,则孔喉渗透率越低;岩石结构越复杂,其非均质性越强,残余气饱和度也越高[6]。初始含气饱和度越小,则残余气饱和度越高[7]。Chris Woods等人通过测试渗透率对残余气饱和度在岩心中分布的影响,却得出相反的结论[8]。
本次研究将通过综合调研国内外文献,总结各类主要试验研究方法和理论模型。根据已有的初始含气饱和度与残余气饱和度关系实验数据,拟合了水驱气藏残余气饱和度经验公式。
1 实验测试方法
1.1 稳态法
稳态法用于测量相对渗透率[9],可靠性强,可在比较宽的饱和度范围内测定相对渗透率。但是此方法的测试实验时间较长,必须在不同气液比达到稳定的条件下进行测试,不易实现。当考虑毛管末端效应时,在进口端直至接近出口端很窄的范围内才会出现饱和度曲线微微上翘的趋势。当稳定状态下流速值适当,且进口端含水饱和度表示整个岩心平均含水饱和度时,毛细管末端效应引起的含水饱和度曲线上翘趋势可以忽略。
1.2 非稳态法
易敏等人根据地下水动力原理推导了利用实验测定数据计算水驱气相对渗透率的公式,并设计了一套回压装置用于非稳态水驱气相对渗透率测定[2]。该实验能在高温高压状态下进行,岩心周围加上围压能较好地满足地层条件下的状况。非稳态法测定气水相渗,是以一维两相渗流理论和气体状态方程为依据,利用非稳态恒压法进行岩样气驱水试验。其主要优点是,所需的仪器设备及时间相对较少。但其并不严格的简化假设导致计算结果不够准确,使得可靠性不高。用非稳态法测试气水相渗时,应根据水气渗流特点选择合理的注入速度,以免发生局部突进形成水锁效应。
1.3 单向与多向自发渗吸法
将饱和气体的岩样底部端面与湿相水接触,此时湿相水自岩样底部逐渐向上吸入,而空气自岩样上端面排出,此方法称为单向渗吸。若将饱和气体的岩样完全放入水中,则为多向渗吸。利用亲水岩样在吸水过程中的毛细管力作为渗吸动力,将水吸入岩样并排驱孔隙中的气体。该实验适用于带有底水驱、砂体分布较广、开采速度较快气藏的残余气饱和度模拟实验。实验中岩样初始含水饱和度是影响残余气饱和度的重要因素,而孔隙度、渗透率对最大残余气饱和度的影响较小。自发渗吸实验理论基础为毛细管自发渗流机理,实验测试对仪器和设备的要求较为简单,实验条件为常温常压,能在较短时间内完成,适用于底水锥进水驱气藏模拟,对带边水水驱气藏或者注水开发水驱气藏适应性较差。
2 残余气饱和度理论模型
1967年,Agarwal对300个渗吸实验数据进行了分析。他考虑了岩样基本物性对残余气饱和度的影响,测试了3类不同物性岩样(非胶结砂岩、胶结砂岩和碳酸盐岩)的残余气饱和度,建立了式(1)所示岩样残余气饱和度经验计算公式[10]:
(1)
式中:Sgr—— 残余气饱和度,无因次;
Sgi—— 初始残余气饱和度,无因次。
1968年,Land研究发现,残余气饱和度随其初始饱和度增加而增加,且同一岩样残余气饱和度的倒数与原始含气饱和度的倒数之差接近某一常数。他拟合出式(2)所示的经验公式[11]:
(2)
式中:Sgr,max—— 最大残余气饱和度,无因次。
1997年,Kleppe等人认为Land模型与岩石类型无关。通过储层模型中的毛管力滞后现象,发现毛管吸入曲线末端最大残余气饱和度与储层残余气饱和度呈线性相关。他们拟合出式(3)所示经验计算公式[12]:
(3)
式中:Sg,max—— 最大含气饱和度,无因次。
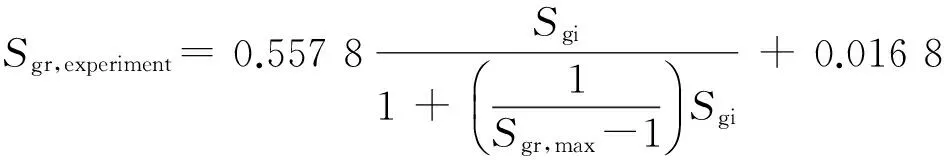
(4)
式中:Sgr,experiment—— 实验测试的残余气饱和度,无因次。
2002年,Holtz等人研究后认为水驱替气体不完全,残余气饱和度由水渗吸进入气藏孔隙与吼道产生,岩石孔隙度、渗透率、毛管压力、束缚水饱和度对残余气饱和度都有影响。他们考虑了孔隙度、渗透率、初始含气饱和度等主要影响因素,推导出式(5)所示经验公式[7]:
(5)
Sgr,max=0.969 6φ+0.547 3
(6)
(7)
(8)
式中:Swirr—— 束缚水饱和度,无因次;
φ—— 孔隙度,%;
K—— 绝对渗透率,10-3μm2。
2002年,Ding等人在加拿大碳酸盐岩气藏研究中认为,残余气饱和度只是其初始饱和度的函数。他们对Agarwal模型进行拟合得到式(9)所示关系式[4]:
Sgr=1.003 3Sgi-0.396 2
(9)
2014年,李久娣等人通过单向渗吸实验数据,发现岩样的残余气饱和度随着岩样初始含水饱和度的增加而减小,认为岩样初始含水饱和度是影响残余气饱和度重要的因素。他们通过拟合实验数据得到式(10)所示初始残余气饱和度与残余气饱和度关系式[13]:
(10)
利用以上各理论模型,可以给出相应气田气体残余量。分析式(1) — 式(10)残余气饱和度理论模型,认为残余气饱和度与岩样类型(砂岩、碳酸盐岩)无关,而是与初始含气饱和度有很大的关联。
3 残余气饱和度的影响因素分析
3.1 残余气饱和度与初始含气饱和度的关系
图1所示为残余气饱和度与初始含气饱和度的关系。由图1可知,当初始残余气饱和度小于0.6时,残余气饱和度随初始含气饱和度增加而增加,随着初始含气饱和度的增加,残余气饱和度增大的趋势逐渐变缓;当初始残余气饱和度大于0.6时,残余气饱和度与初始含气饱和度并不是密切相关,但大致上随着初始含气饱和度增加,残余气饱和度在降低。其主要原因是,初始含气饱和度较低,水湿岩石、水体以薄膜形式存在于岩石内表面,气体流动主要通道(孔隙、喉道和裂缝)未被堵死,初始含气饱和度较大时,对残余气流动性的影响较小。
3.2 残余气饱和度与孔隙度、渗透率的关系
图2所示为残余气饱和度与孔隙度的关系。由图2可知,孔隙度在22%以内,残余气饱和度随孔隙度的增加而增加,且增加趋势逐渐变缓。孔隙度在22%左右时,残余气饱和度都偏高,其主要原因是孔隙度在22%时存在游离气和吸附气,且水在孔隙喉道中造成喉道堵塞,导致游离气堵塞在孔隙喉道中,而吸附气脱附较少导致残余气饱和度偏高。

图1 残余气饱和度与初始含气饱和度的关系

图2 残余气饱和度与孔隙度的关系
图3所示为残余气饱和度与渗透率的关系。由图3可知,残余气饱和度随气测渗透率的增加而逐渐下降,最后渗透率达到6 000×10-3μm2时趋向于平缓,此时残余气饱和度在20%左右。 当渗透率小于1 000×10-3μm2时,残余气饱和度与渗透率相关度较小,无明显变化趋势,且残余气饱和度主要集中在0.3左右,渗透率对残余气饱和度的影响不大。 当渗透率较大时,残余气饱和度与渗透率呈弱相关性,即随着渗透率的增加,残余气饱和度减小。
4 实验数据与理论模型对比分析
4.1 初始含气饱和度和残余气饱和度
以孔隙度、渗透率、初始含气饱和度等主要影响因素为参考进行计算,残余气饱和度计算所需要的数据来源于其他文献。表1所示为残余气饱和度计算数据。

图3 残余气饱和度与渗透率的关系

来源文献数据类型样本个数[1]孔隙度,渗透率,初始含气饱和度,残余气饱和度8[2]孔隙度,渗透率,初始含气饱和度,残余气饱和度5[6]孔隙度,渗透率,初始含气饱和度,残余气饱和度11[13]初始含气饱和度,残余气饱和度40[14]孔隙度,渗透率,初始含气饱和度,残余气饱和度8
将初始含气饱和度与残余气饱和度实验数据与其他理论模型进行对比。图4所示为实验数据与其他理论模型数据对比。对比可知,与实验结果相比,Ding模型、Li模型、Agrawal模型均存在较大误差。
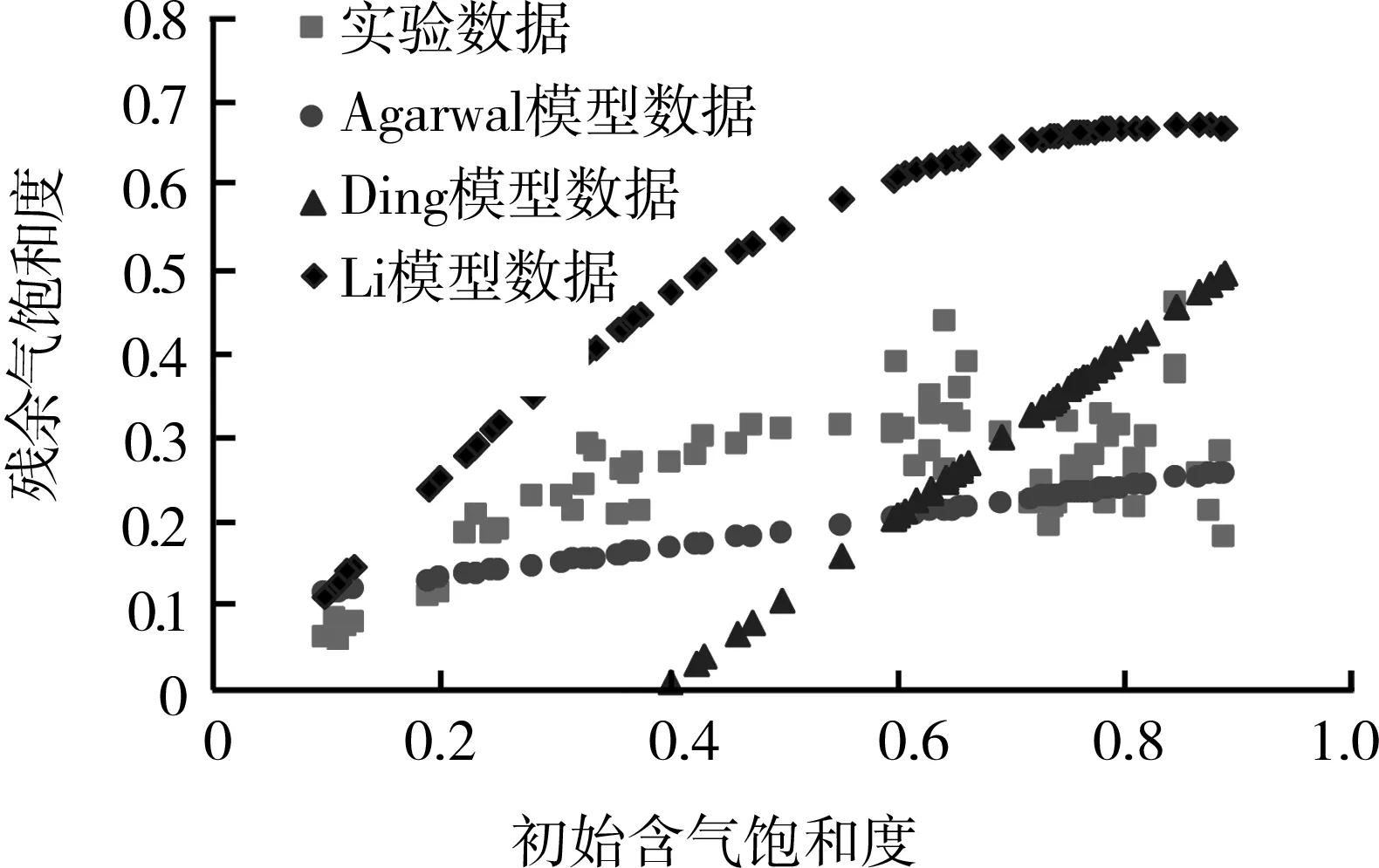
图4 实验数据与其他理论模型数据对比
图5所示为残余气饱和度与初始含气饱和度的关系。分析可知,当残余气饱和度小于0.6时,初始含气饱和度与残余气饱和度呈较强的相关性,个别实验数据可能出现偏差,但总体规律不会变化。利用二项式方程进行拟合,发现拟合关系曲线与实验值拟合精度较高,R2可达0.920 7。

图5 残余气饱和度与初始含气饱和度的关系
当Sgr小于0.6时,初始含气饱和度占主导作用,若不考虑孔隙度、渗透率等其他因素的影响,可利用二项式拟合数据,得到公式(11):
Sgr= -0.008 9Sgi2+ 1.164 3Sgi-4.680 5
(11)
4.2 孔隙度、渗透率、初始含气饱和度和残余气饱和度
考虑孔隙度、渗透率、初始含气饱和度对残余气饱和度的影响,因孔隙度、渗透率对残余气饱和度影响较小,需取低孔渗权重,于是将对数形式下孔隙度和渗透率的乘积(即F影响因子)作为变量,如式(12)所示:
F=ln(Kφ)
(12)
将实验数据带入式(13)中进行计算:
Sgr=a1+a2F+a3F2+a4Sgi+a5Sgi2+a6Sgi3+a7Sgi4
(13)
利用1stopt软件对实验数据进行拟合,得到参数值a1、a2、a3、a4、a5、a6、a7(见表2)。

表2 参数值
5 结 语
稳定法具有所测数据可靠性高的特点,但测试所用时间较长,且不易实现,给实验增加了难度。非稳态法、单相和多向渗析法均具有测试时间短的优点,但非稳态法能用于高温高压环境下的测试,适应地层条件,而单相和多向渗析法只能用于常温常压环境下的测试,适应范围较窄。
国内残余气饱和度理论模型研究通常倾向于考虑初始含气饱和度的影响。在此基础上考虑孔隙度与渗透率的影响,可以进一步补充完善理论模型。
初始含气饱和度是影响残余气饱和度的重要因素。当初始残余气饱和度小于0.6时,拟合不同类型气藏初始含气饱和度与残余气饱和度,得到的影响规律较为准确。模型中综合了多种残余气饱和度的影响,更能反映出真实的残余气饱和度水平。
[1] 周显民.喇嘛甸油田水-气相对渗透率曲线实验研究[J].大庆石油地质与开发,1988(2):29-36.
[2] 易敏,郭平,孙良田.非稳态法水驱气相对渗透率曲线实验[J].天然气工业,2007(10):92-94.
[3] KANTZAS A,DING M H,JONE L.Residual gas saturation revisited[G].SPE 59782,2000.
[4] DING M ,KANTZAS A.Residual gas saturation investigation of carbonate reservoir from western canada[G].SPE Gas Technology Symposium,to be Held in Calgary,Alberta,2002.
[5] DING M,KANTZAS A.Evaluation of gas saturation during water imbibition experiments[G].CIM 2003-021,2003.
[6] MULYADI H,AMIN R,KENNAIRD T,et al.Measurement of residual gas saturation in water-driven gas reservoirs:comparison of various core analysis techniques[G].SPE 64710,2000.
[7] HOLTZ M H,JOHN A,KATHERINE G,et al.Petrophysical characterization of permian shallow-water Dolostone[G].SPE 75214,2002.
[8] CHRIS W,TIM C.Identifying,quantifying and modelling residual gas[G].SPWLA 53rd Annual Logging Symposium,2012.
[9] M·霍纳波.油藏相对渗透率[M].马志元,高雅文,译.北京:石油工业出版社,1989:6-10.
[10] AGARWAL R G.Unsteady-state performance of water-drive gas reservoirs[D].Texas:Texas A & M University,1967:46-59.
[11] LAND C S.Calculation of imbibition relative permeability for two-and three-phase flow from rock properties[J].SPE Journal 1968,8(2):149-156.
[12] KLEPPE J P,DELAPLACE R.Representation of capillary pressure hysteresis in reservoir simulation[G].SPE-38899-MS,1997.
[13] 李久娣,胡科.DH气藏残余气饱和度实验研究[J].西南石油大学学报(自然科学版),2014(1):107-112.
[14] FIROOIABADI A, OLSEN G, van GOLF-RACHT T.Residual gas saturation in water-drive gas reservois[C].SPE-163355-MS,1987.
Experiment and Theory Prediction Model of Residual Gas Saturation in Water Drive Gas Reservoir
LUOQiangSUNLeiPANYiWANGQiong
(State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China)
Based on the comprehensive summary about the domestic and foreign research on experimental methods, influential factors and theory model of residual gas saturation, we found that the initial gas saturation and residual gas saturation are highly correlated. According to the experimental data, when initial gas saturation is less than 0.6, it is the dominant influence on residual gas saturation. Finally, a theoretical calculation model of residual gas saturation is established considering a number of influencing factors, such as permeability and porosity and so on.
initial gas saturation; porosity; permeability
2016-08-12
国家科技重大专项“海外大陆边缘盆地勘探开发实用新技术研究”( 2011ZX05030-005)
罗强(1992 — ),男,西南石油大学在读硕士研究生,研究方向为流体相态、相渗驱替理论。
TE375
A
1673-1980(2017)02-0008-04

