静态与动态Mirrlees模型的最优税收理论*——拉格朗日泛函的应用

赵晓军 王龙 王小华 李德轩

（1．北京大学经济学院北京100871）

（2．中央财经大学中国经济与管理研究院北京100081）

（3．中国传媒大学动画与数字艺术学院北京100024）

静态与动态Mirrlees模型的最优税收理论*
——拉格朗日泛函的应用

赵晓军1王龙1王小华2李德轩3

（1．北京大学经济学院北京100871）

（2．中央财经大学中国经济与管理研究院北京100081）

（3．中国传媒大学动画与数字艺术学院北京100024）

本文利用拉格朗日方法重新解决Mirrlees（1971）和Golosov等（2003）的模型，得到一些更为丰富的结果。Golosov等（2003）仅仅求解了最优的资本收入税，本文同时求解了动态情形下的最优资本收入税和劳动收入税，从而使得比较静态和动态情形下的Mirrlees模型成为可能。本文的结论是动态和静态的情形下最优的劳动收入税形式一致，并当效用函数关于劳动能力存在乘积意义上的可分，劳动收入税可以为0。在研究了最优税收政策后，本文模拟了相关结果，给出一些图表用以佐证提出的观点。

Mirrlees模型 信息不对称 Lagrange泛函

一、引言

最优税收理论，传统上有两种方式来描述。第一类被称为次优税收理论，它是将政府与经济个体认为是互相博弈的双方，双方的博弈方式是Starkelberg博弈，最优的税收政策就是Starkelberg博弈的均衡策略。次优税收理论较好地描述了税收的本质问题，但是这种理论往往预先假设税收的形式，并且其政策往往具有时间不一致性的问题。于是突破次优税收理论一度成为经济学家的关注热点。还有一类最优税收理论利用不完备市场的结构造成最优的分配与理想中的分配有一定的摩擦，于是在分散经济中就可以利用扭曲性税收政策来平滑这一摩擦，使得分散经济的分配和具备摩擦的计划者经济一致。不完备市场中具备摩擦的经济种类较多，大体上有两种类型的摩擦。第一类是由市场的法律法规限制而形成的摩擦，通常体现为借贷约束、市场准入条件、最低行业标准以及在发展中国家广泛存在的金融市场的各类加以约束。①如我国的金融市场是不完全市场化的，它不允许卖空，涨停涨跌等限制。这类约束往往是人为地对市场的限制，在实际操作中比较容易去除。并且随着时间的推移和市场化进程的加快，此类约束逐渐软化，对经济的影响越来越微弱。第二类摩擦是由不对称信息引起的，最早Mirrlees（1971）考察了不对称信息下的最优劳动收入税，得出税收与劳动能力之间的Logistic关系。指出税收政策的设计为了更好地激励全体公民的劳动，同时，由于信息不对称为经济内生的约束，它不可能简单地通过法规的设计来得到约束的软化，所以，自Mirrlees（1971）之后，大批经济学家集中在信息不对称领域，当前信息经济学已经成为这个时代经济学的主流。

虽然Mirrlees（1971）最早研究的是最优税收问题，但那只是在静态的框架下展开，得到的结果并不是特别丰富。之后的经济学家如Stiglitz，Akerlof和Spence将信息经济学发扬光大，但他们研究的领域已然脱离了最优税收的框架。Golosov等（2003）首次将Mirrlees（1971）的模型推广到动态的框架，得出最优的资本收入税为正的结论。但是由于优化问题求解方法上的限制，Golosov等（2003）并没有解决相关的一些重要问题，并且没有可能与静态的Mirrlees模型进行比较。

本文利用Lagrange泛函的方法统一解决了静态和动态情形下，带有信息不对称的Mirrlees模型。得到比Golosov等（2003）更丰富的结果，给出最优税收的显示表达式，并比较了动态和静态框架下的Mirrlees模型，得到两者的劳动收入税形式一致的结论。最后，本文给出数值模拟，刻画税负承担人群。接下来的行文安排如下：在第二节讲述静态Mirrlees模型；第三节讲述动态Mirrlees模型；第四节模拟各种最优税收的结果；第五节进行总结。

二、静态情形

1．基本模型设定

静态的Mirrlees模型比较简单，设θ为经济个体的劳动能力，它是概率空间(Ω,F,μ)上的随机变量，它的像集为Θ。因此，经济个体的有效劳动y=lθ，其中l为其劳动时间。个体的效用函数建立在消费c和劳动l上，记为u(c,l)=u(c,y/θ)。设生产函数为H(Y)，其中为加总的有效劳动，则计划者的最优化问题为：

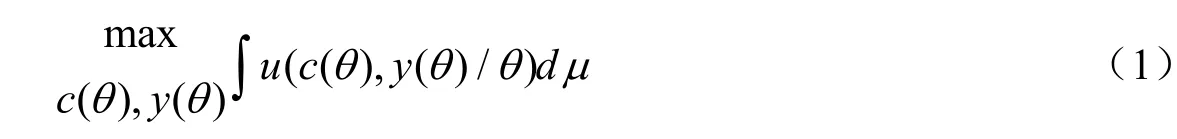
受到如下资源约束：

和IC约束：

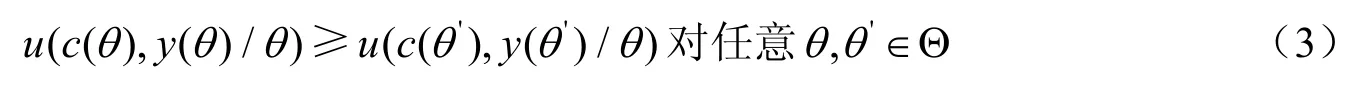
这样，就构建了静态框架下的Mirrlees模型，下面利用Zhao and Gong（2009）介绍的拉格朗日泛函的方法求解这一模型。

2．计划者经济模型求解

若定义λ为资源约束（2），λ(θ,θ')为IC约束（3）的拉格朗日乘子，则由赵晓军（2010）命题2.8可得：

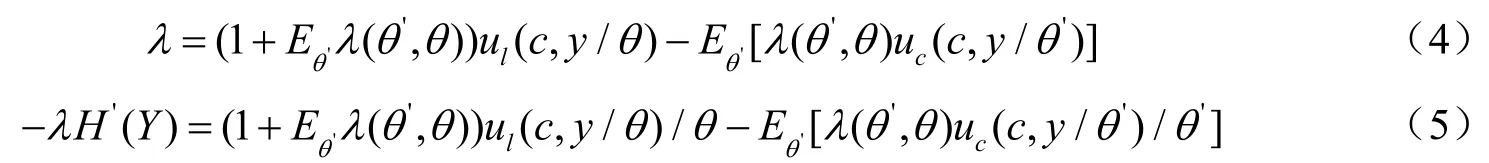
和赵晓军（2010）一样，若对效用函数u(c,y/θ)没有一些特别限制，则无法得到更有意义的结论。为此，下面假设了两种情形：

情形1.

则方程（4）和（5）成为：

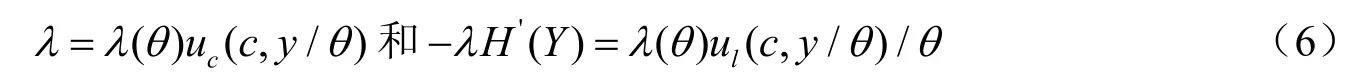
在上式中消去λ和λ(θ)得到最终的一阶条件：

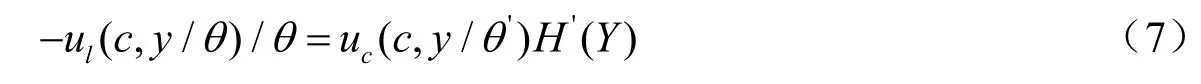
情形2.

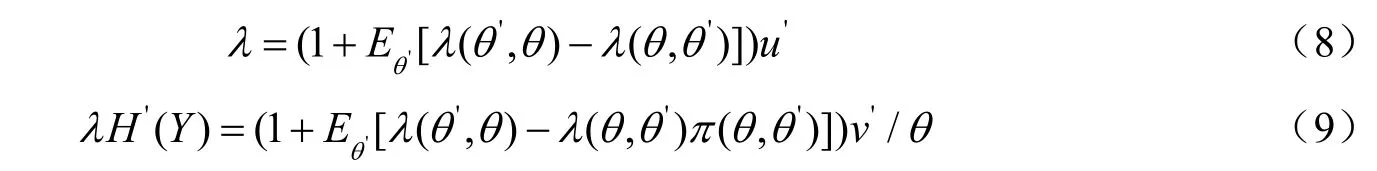
在上式中消去λ得到最终的一阶条件：

为了得到最优税收政策，下面考察分散经济情况。

3．分散经济中的实现

在分散经济中，具备能力为θ的个体优化问题为：

受约束于

其中τw为劳动收入税率，χ(θ)为政府的转移支付。上述问题的最优性条件为：

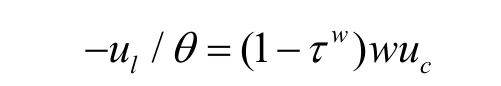
政府的预算约束平衡为：

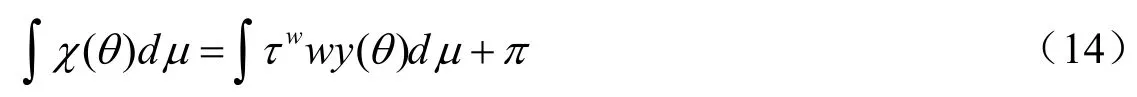
因此在宏观均衡中将得到：

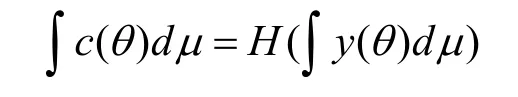
这和资源约束（2）是一致的。

在情形1中，如果要求分散经济达到计划者经济配置，则τw=0。而在情形2中，则需要：

这是依赖于状态θ的税收政策。

需要说明的是，在情形1中得到的最优劳动收入税为零，这与Cham ley（1986）和Judd等（1985）的结论相同。有一大类的效用函数满足情形1的假设，如：

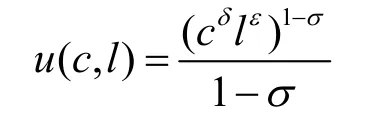
其中θ,ε和σ都是大于0的常数，则：

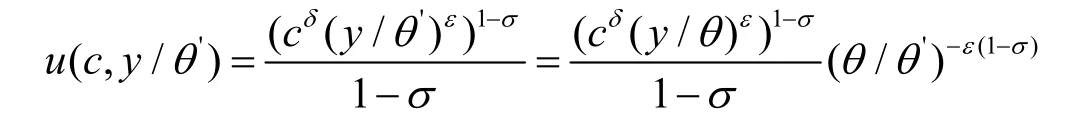
因此，此类效用函数满足情形1的假设，于是此时的最优资本收入税率为0。

图1 静态Mirrlees模型最优劳动收入税与能力关系

上图的相关常数设定如下，σ=2,γ=0.5，设H(Y)=Y0.7，并假设能力θ是区间[2,22]上的均匀分布。下面进入动态Mirrlees模型的讨论。

三、动态情形

本部分沿用Golosov等（2003）的动态Mirrlees模型，重新检验他们的结论，并全面解决Golosov等（2003）框架下的最优税收问题。首先来描述经济的基本元素，它主要包括对经济个体效用、私有信息的描述，对生产的描述。

假设经济持续T期，经济个体分布在[0,1]闭区间上。对于任意经济个体j∈[0,1]，设他在t期具有劳动能力并假设对于不同个体j是独立同分布的，随机过程定义在概率空间(Ω,F,μ)上，对于递增的事件流Ft是适应的。和赵晓军（2010）一致，定义F为所有事件流的并集，即

在t期经济个体的效用函数建立在消费和劳动上，其有效劳动考虑到θt为私有信息，将t期的效用函数表达成则劳动能力序列为的经济个体事后折现效用为

从上一部分的讨论，可以得到最优税收政策需要分散经济的最优性条件，为此，下面先介绍分散经济。

1．分散经济

分散经济分析的一般思路是在固定政府政策下，经济达到的均衡。此时的经济有三方参与者：消费者、厂商和政府。对劳动能力序列为的消费者而言，就是在财富约束下的期望折现效用最大化。也即：

受约束于

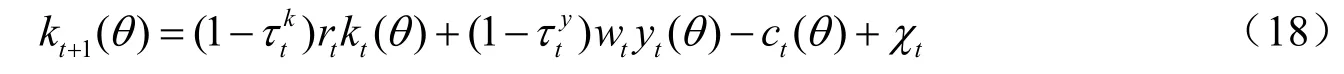
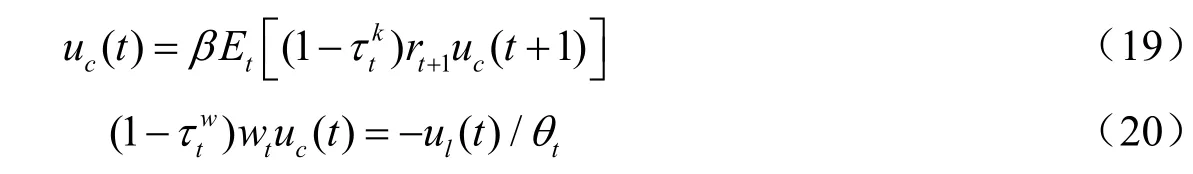
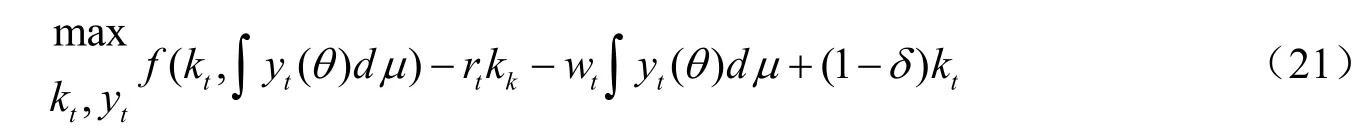
其中kt为t期的社会总资本，为社会加总的有效劳动，这个优化问题的一阶条件为

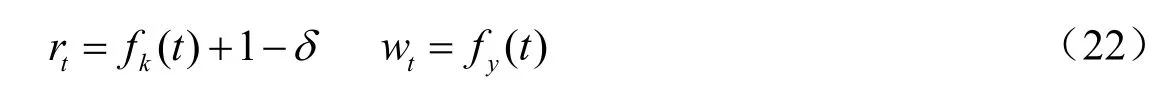
下面考虑政府的预算约束平衡，保证每期的税收收入全部用于转移支付，即

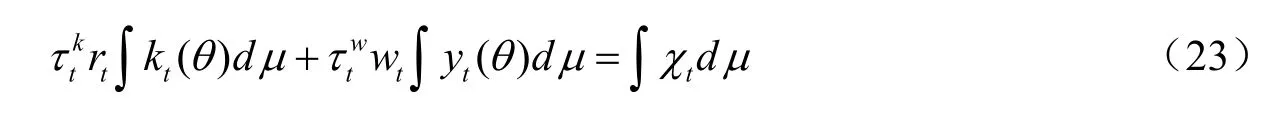
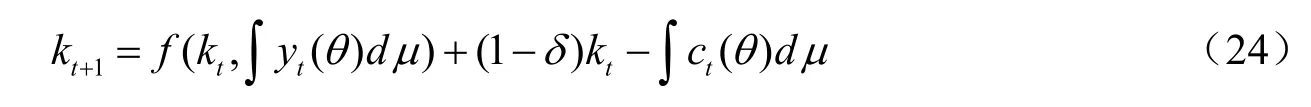
同时消费者在均衡时的一阶条件变成

以上两个式子就是分散经济均衡时的最优性条件，下面计算在信息不对称下的计划者经济下的最优性条件，比较两者的最优性条件，得到最优税收。

2.计划者经济模型求解

考虑此时政府充当社会计划者的角色，它组织生产，分配资源。但是它只能观测到经济个体的有效劳动不能知道经济个体的劳动能力，于是在资源分配时，它需要经济个体汇报自己的真实类型。因此，它的分配应该使得每种类型的经济个体的事后效用在真实汇报情形下最大。于是计划者经济的优化问题如下：

受到资源约束

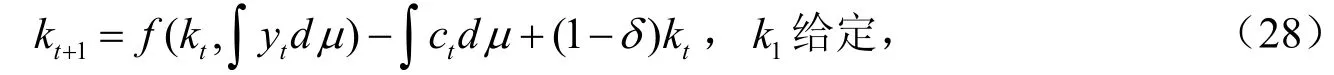
和如下的激励相容约束

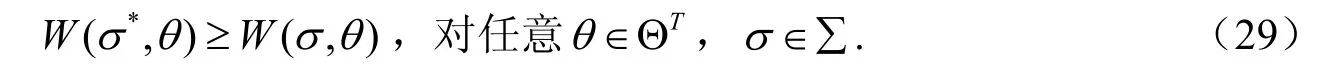
其中W(σ,θ)为能力序列为θ的个体在汇报策略为σ:ΘT→ΘT下的事后折现效用。即：

记所有汇报策略σ组成的集合为∑，上述激励相容约束（29）还可以进一步改写成：

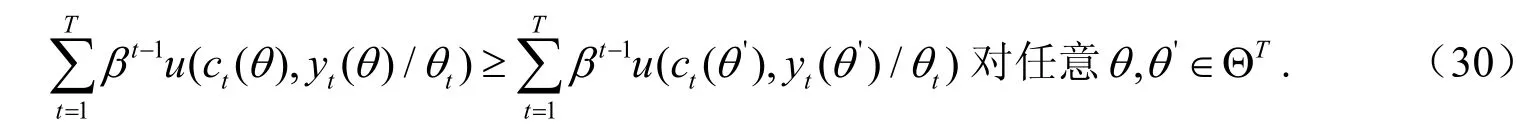
记λt为资源约束（28）的拉格朗日乘子，为IC约束（30）的拉格朗日乘子，应用拉格朗日泛函的方法，得到

同上一节的讨论一样，如果不给出效用函数的进一步性质，我们依然无法分析上述最优性条件。为此，分以下两种情形讨论。

情形1.

注意λt为非随机变量，利用上式可得

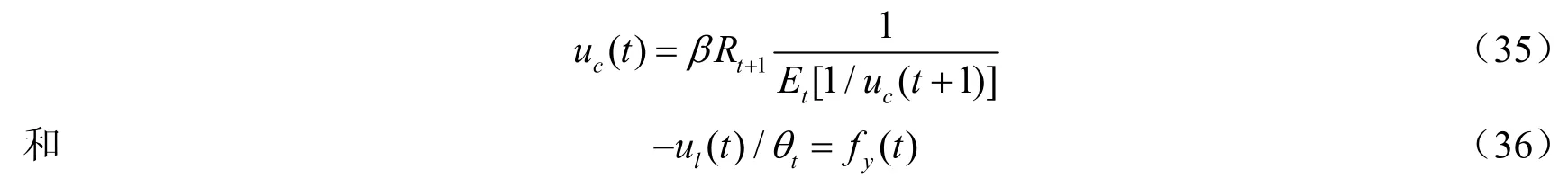
等式（35）就是“逆欧拉方程”，和Golosov等（2003）一致。比较（36）和（26），得到此时的最优劳动收入税为零，即：

同时比较（35）和（25）得到：

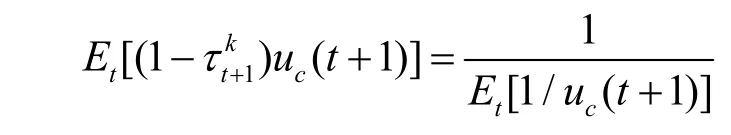
由此可得：

其中ε满足

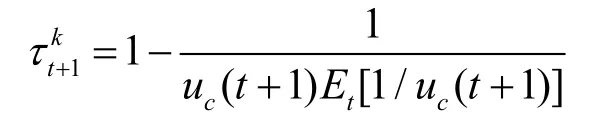
（37）表明此时的最优劳动收入税为零，这和静态的情形1一致，（38）表明最优的资本收入税可以有多种选择，这一结论与Zhu（1992）的结论类似，在那篇文文中，考虑是一个带生产冲击的经济，其最优的资本收入税也可以有多重选择。若要求则唯一的最优资本收入税率由（39）给出，由Jesson不等式，可得此时的税率大于0，这个税率和Golosov等（2003）一致，但是这里关于效用函数的假设不同于Golosov等（2003）。

情形2.

方程（41）再次重复了Golosov等（2003）的结论，而（42）是雷同于静态Mirrlees模型的结果，无非此时加上了条件期望算子Et，于是动态不对称信息下的最优劳动收入税和静态的结果一致。但是方程（42）在Golosov等（2003）中没有得到，事实上，利用Rogerson（1985）提出的最小资源对偶方法是无法得到这一最优性条件的，只有通过拉格朗日泛函的方法得到。

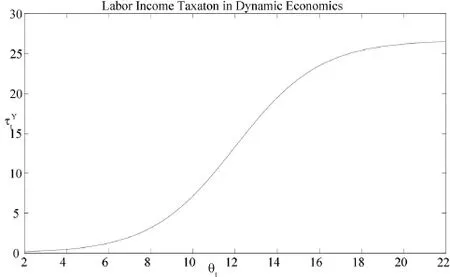
图2 动态Mirrlees模型最优劳动收入税和能力关系

下面考察此时的资本收入税与劳动能力的关系。对能力序列为θ的经济个体在t期的资本收入税收为：

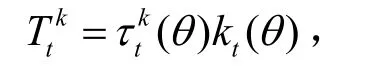
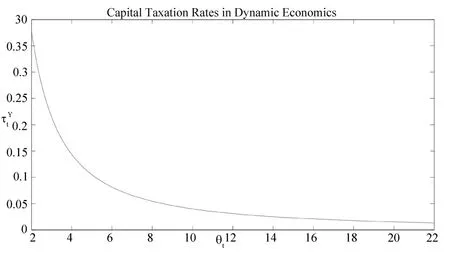
图3 动态Mirrlees模型最优资本收入税率与劳动能力关系

从以上的求解过程中，仅可以得到最优消费路径ct(θ)、最优有效劳动供给路径yt(θ)和最优社会资本路径kt。无法得到个人的财富路径kt(θ)，从分散经济的财富积累方程（18）看出，个人的财富积累路径依赖于政府转移支付政策的实施。而转移支付政策只要在总量上满足（23）即可。于是政府可以通过差异性转移支付使得每一位经济个体在每一期的财富水平相同，即kt(θ)=kt。从这个意义上说，资本收入税率之间的差异可以反映资本收入税税收收入之间的差异。据此，在本文的下述行文过程中，如没有特别强调，在描述资本收入税和劳动能力之间的关系时，都采用资本收入税率与劳动能力之间的关系替代。沿用图2的数据，图3给出资本收入税率与劳动能力之间的函数关系。

四、最优税收的数值模拟结果

本节综合本文前几节的内容，进行数值模拟。采用的效用函数统一为生产函数采用劳动能力{θt}设为独立同分布的序列，其共同分布为[2,22]上的均匀分布。参数的设定在具体的数值模拟结果介绍时指出。

1.最优资本收入税

沿用图3的解释，个人的资本存量可以通过政府的差异性转移支付得到每一期都相等。于是资本收入税率之间的差异反映税收收入之间的差异，在以下关于资本收入税的图表都将使用税率和能力之间的关系表达。首先来考察随时间变化，资本收入税率的变化趋势。

图4反映随时间增加，资本收入税率不断增加。同时注意到在t比较小时，税率随能力增加而减少，体现对高能力者的激励作用。但是当t比较大时，对高能力者反而要征收高额资本收入税，这体现随着经济结束日子的临近，已经没有必要激励高能力者，可以对其实施重税策略。

图4 资本收入税与劳动能力关系随时间变化趋势

同时注意到，在t=15时，能力约超过17的人其资本收入税随能力增加而增加，体现高能力者在经济结束临近时的惩罚性税收措施。并且在t=20时，这个高能力高税收的政策又将人群提前到能力约大于13的地方，即经济结束的前夕，资本收入税有不断提前的惩罚效应。下面考察资本收入税与参数σ之间的关系，见图5。

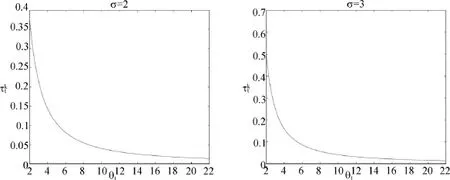
图5 资本收入税与劳动能力关系随σ变化趋势

图5反映的是随着风险回避系数σ的增加，资本收入税与劳动能力构成的函数更加地凸向原点，但总体的递减关系并没有变化。值得注意的是当σ增大时，相同能力的经济个体税负增加，这体现资本收入税与劳动能力构成的函数上移。可以预测，当σ充分大时，这一图像最终也会形成类似图4的后两幅子图的情况。

2．最优劳动收入税

不同于研究资本收入税的逻辑，这里的所有的图像反映了劳动收入税与劳动能力之间的关系，而不再是税率和劳动能力之间的关系。采用上一小节的比较方式，同样考察劳动收入税与劳动能力之间的关系随时间t、风险回避系数σ的变化趋势。首先给出随时间的变化趋势。

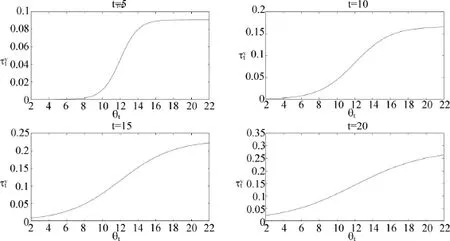
图6 劳动收入税与劳动能力关系随时间t变化趋势

图6反映了劳动收入税和劳动能力之间的Logistic关系，并且随时间增加，这个曲线更加趋于平坦。这表明，随着经济的结束来临，边际劳动收入税增加的人群在不断地扩张，体现对高能力者的激励效果不断减少。而边际劳动收入税增加的幅度也在减少，处于中间能力层的边际税负减轻，而高能力和低能力者的边际税负增加。再看资本收入税和劳动能力之间关系随风险回避系数σ的变化，如图7。

图7 劳动收入税与劳动能力关系随σ变化趋势

图7表明随着风险回避系数σ的增加，劳动收入税和劳动能力之间的Logistic曲线更加平坦，但是税负同比增加。相当于Logistic曲线上移且更加平坦。其经济解释为人们对消费风险态度增加，就会谨慎消费，为此，通过减少中间能力层人群的边际税负，通过财富效应提高其对消费的信心。这种改变体现了Logistic曲线更加平坦，同时需要增加高能力者和低能力者的边际税负，因为对高能力者而言，消费风险的增加和财富效应并不在很大程度上影响其消费；而对低能力者而言，他们本身的消费就很低。因此，对于关注社会福利的政府来说，增加少量的高能力者和低能力者的边际税负，减少大量中等能力者的边际税负有助于提高社会福利水平。

五、本文小结

本文利用拉格朗日方法重新检验了Mirrlees（1971）和Golosov等（2003）的模型，改进了他们的结论。并在不对称信息经济中在动态的情形求解了最优劳动收入税，给出了相关的数值模拟结果和解释。使得Mirrlees模型在静态和动态情形下有比较的可能。同时，本文给出的数值模拟结果也使得我们对信息不对称下的最优税收结果有更好的认识。

Zhao和Gong（2010a）和Zhao和Gong（2010b）两文中，将充分利用拉格朗日方法求解在不对称信息经济中的动态最优税收政策。但是关注的重点将不再一定为税收政策了，如在Zhao and Gong（2010a）中就将关注的重点放在教育的公共投资和私人投资上。在那时同样有最优税收政策的参与，但同时也有各类对应性转移支付的政策，此时考察的应该是最优的财政政策。在Zhao和Gong（2010b）中将关注的重点放在财政分权的结构上，得到的最优财政政策分为两类：一类是地方政府的最优税收政策，另一类是中央政府的最优税收和对应性转移支付政策。

参考文献：

1.赵晓军：《非对称信息下的最优税收理论研究》[D]，北京大学博士毕业论文，2010年。

2.Atkinson,A.and J.E.Stiglitz,1976,“The Design of Tax Structure:Direct Versus Indirect Taxation”[J],Journal of Public Economics,Vol 6,No.3:55-75.

3.Atkinson,A.and J.E.Stiglitz,1980,Lectures on Public Econom ics,[M],New York,NY:M cGraw-Hill.

4.Cham ley,C.1986,“Optimal Taxation of Capital Income in General Equilibrium w ith Infinite Lives”[J],Econometrica,Vol 54,No.2:607-622.

5.Diamond,P.and J.A.Mirrlees,1978,“A Model of Social Insurance w ith Variable Retirement”[J],Journal of Public Economics,Vol 10,No.3:295-336.

6.Diamond,P.and J.A.Mirrlees,1986,“Payroll-Tax Financed Social Insurance w ith Variable Retirement”[J],Scandinavian Journal of Economics,Vol 17,No.4:25-50.

7.Golosov,M.,Kocherlakota,N.and O.Tsyvinski,2003,“Optimal Indirect and Capital Taxation”[J],Review of Economic studies,Vol 70,No.5:569-587.

8.Gong,L.T.,Zhao,X.J.,Yang,Y.H.and H.F.Zou,2010,“Stochastic Grow th w ith the SocialStatus Concern: The Existence of a Unique Stable Distribution”[J],Journal of Mathematical Economics,Vol 46,No.4: 505-518.

9.Judd,K.,“Redistributive Taxation in a Simple Perfect Foresight Model”[J],Journal of Public Economics,1985,Vol 28,No.1:59-83.

10.Kocherlakota,N.,1998,“The Effects of Moral Hazard on Asset Prices When Financial Markets Are Complete”[J],Journal of Monetary Economics,Vol 41,No.4:39-56.

11.Kocherlakota,N.,2005b,“Zero Expected Wealth Taxes:A Mirrlees Approach to Dynamic Optimal Taxation”[J],Econometrica,Vol 73,No.4:1587-1621.

12.Kocherlakota,N.,2004,“Wedges and Taxes”[J],The American Economic Review,Vol 94,No.5:109-113.

13.Mirrlees,J.,1971,“An Exploration in the Theory of Optimum Income Taxation”[J],Review of Economic Studies,Vol 38,No.2:175-208.

14.Mirrlees,J.,1976,“Optimal Tax Theory:A Synthesis”[J],Journal of Public Economics,Vol 6, No.5:327-58.

15.Rogerson,W.,1985,“The First-Order Approach to Principal-Agent Problems”[J],Econometrica,Vol 53, No.5:1357-67.

16.Zhao,X.J.and L.T.Gong,2007,“A Generalization of Duality Approach in Stochastic Grow th”[D], Working Paper Peking University.

17.Zhao,X.J.and L.T.Gong,2009,“The First-Order Conditions of Dynam ical Optimal Problems w ith Incentive Compatible Constraints”[D],Working Paper Peking University.

18.Zhao,X.J.and L.T.Gong,2010a,“The Optimal Taxation Theory w ith Labor Ability Evolution Mechanism”[D],Working Paper Peking University.

19.Zhao,X.J.and L.T.Gong,2010b,“The Optimal Fiscal Policy in the Fiscal Decentralized Econmy w ith Asymmetric Information”[D],Working Paper Peking University.

20.Zhu,X.D.,1992,“Optimal Fiscal Policy in a Stochastic Grow th Model”[J],Journal of Economic Theory, Vol 58,No.2:250-289.

（H）

*本文为国家社科基金重大项目（批准号：15ZDA007）的阶段性成果，感谢中央财经大学科研创新团队支持计划的资助，作者感谢匿名审稿人提出的宝贵意见，文责自负。