基于双树复小波变换的BivaShrink自选窗图像去噪算法

付康 汤辉+孙丹 刘波平 王蕾

摘要：在小波变换理论和双变量模型的研究基础上，本文提出了一种BivaShrink自选窗算法，该算法根据邻域内小波系数的相关度大小自适应选取邻域窗口。最后将双树复小波变换应用在BivaShrink自选窗图像去噪算法中。实验结果证明，BivaShrink自选窗优于BivaShrink 去噪算法，与传统的离散小波变换相比，双树复小波自选窗图像去噪效果优于BivaShrink自选窗。

关键词：小波变换；图像去噪；双变量模型；双树复小波变换

中图分类号：TN911.73 文献标识码：ADOI：10.3969/j.issn.10036199.2017.01.022

1引言

现如今图像已经成为大家经常要用到的信息，但图像中总是参杂着各类的噪声，会严重影响到图像处理和图像通信，需要对图像进行去噪处理。对图像去噪而言，如何保留有用信息和消除噪声是一个两难的问题[1]。

小波理论有优良的时频局部化、尺度变化和方向性特点，随着它的不断改进和完善，小波分析已经应用到各个学科领域[2]。与傅立叶分析将信号分解成一系列不同频率的正弦波的叠加一样，小波分析是将信号分解为一系列小波函数的叠加，而这一系列小波函数都是由母小波函数经过平移和尺度伸缩得来。小波分析在时域和频域同时具备良好的局部化性质，对高频成分采用逐渐精细的时频域取样步长，从而可以聚焦到任何细节，优于傅立叶分析，被称为“数学显微镜”[3-4]。本文以小波分析理论为工具，结合小波系数的层内和层间相关性，基于小波系数双变量模型，改进论证了一种自适应选取邻域窗口的图像去噪算法。由于双树复小波变换不仅有时频局域特性和多分辨特性，还具有平移不变性和方向选择性优势，最后将双树复小波变换应用于该算法。

2双变量模型自适应选取邻域窗口算法

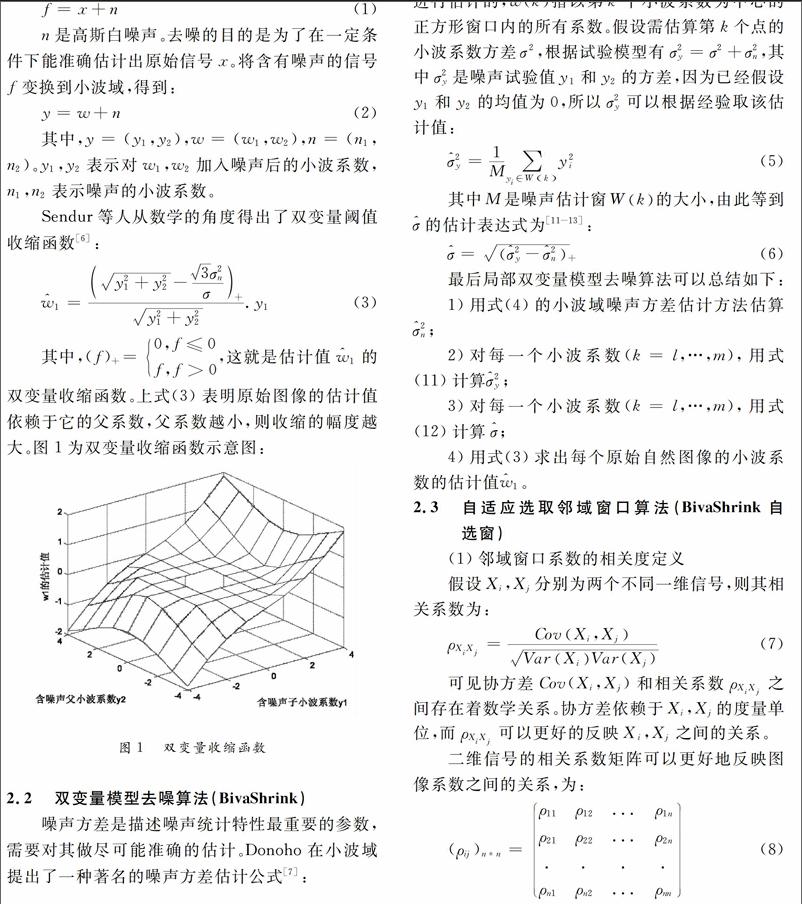
Sendur等人已经从数学的角度出发提出双变量萎缩函数和双变量模型概率密度分布函数来描述小波系数父、子间的相互关系，双变量模型属于一种小波系数层间模型[5]。

是邻域滑动窗口。通过比较式（9）的相关度系数θ，可以判定上述矩阵内待阈值化系数和其余小波系数之间的关联程度，相关度系数θ越大，关联程度也越大，进而选取关联程度最大的窗口为其邻域滑动窗口[14-15]。

（2）双变量模型自适应选取邻域窗口算法

在双变量模型局部自适应去噪算法中，边缘方差的估计采用固定的正方形窗口，如3*3、5*5、7*7邻域窗口，无法根据图像自身的特性自适应选择邻域窗口，影响到了图像去噪效果。所以本文提出一种根据邻域内小波系数的相关度来自适应选取合适邻域窗口的去噪算法，步骤如下：

1）将含有噪声的图像进行二维离散小波变换，分别得到各子带各层图像小波系数；

2）在各个高频子带上，对小波系数用双变量模型做局部自适应去噪处理如下：

a）在各层各个子带中，以待操作小波系数为中心，分别比较计算邻域窗口为3*3、5*5、7*7的相关度系数θi（i=1，2，3）；

b）计算比较三个固定滑动窗口的相关度系数，将最大相关度系数θmax 的邻域窗口作为当前待操作小波系数的窗口；

c）然后得到边缘方差的估计；

d）最后计算小波系数的估计1。

3）将去噪滤波后的高频子带小波系数和低频小波系数进行二维离散小波重构，最终可得到去噪后的图像。

3双树复小波变换的自适应选窗图像去噪算法

由于传统抽取小波不具备平移不变性以及只有有限的方向选择等缺点，将具备平移不变性和更多方向性选择等优点的双树复小波变换应用于双变量模型图像去噪算法中，根据邻域小波系数双变量模型和相关度大小，将双树复小波变换应用于提出的一种邻域小波系数相关度自适应选取邻域窗口的图像去噪算法（邻域窗口包括7*7、5*5、3*3）中，最后进行matlab试验仿真，并与传统的固定邻域窗口双变量模型和传统离散小波变换图像去噪效果相比较。

3.1双树复小波变换自适应选窗算法框图实现

传统离散小波的局限性问题一般可以通过复小波变换解决。为此，Kingsbury等人提出双树复小波变换（DTCWT），不仅可以拥有一般复小波的优点，而且可以实现完全重构[16-17]。

复小波为：

ψt=ψrt+jψit （10）

ψrt，ψit為表示复小波的实部和虚部，但它们均为实函数。双树复小波ψt=ψrt+jψit具有频谱单边性的良好性质，且在二抽样情况下有频率无偏性和良好的平移不变性，这些都是双树复数小波变换的优势[18]。

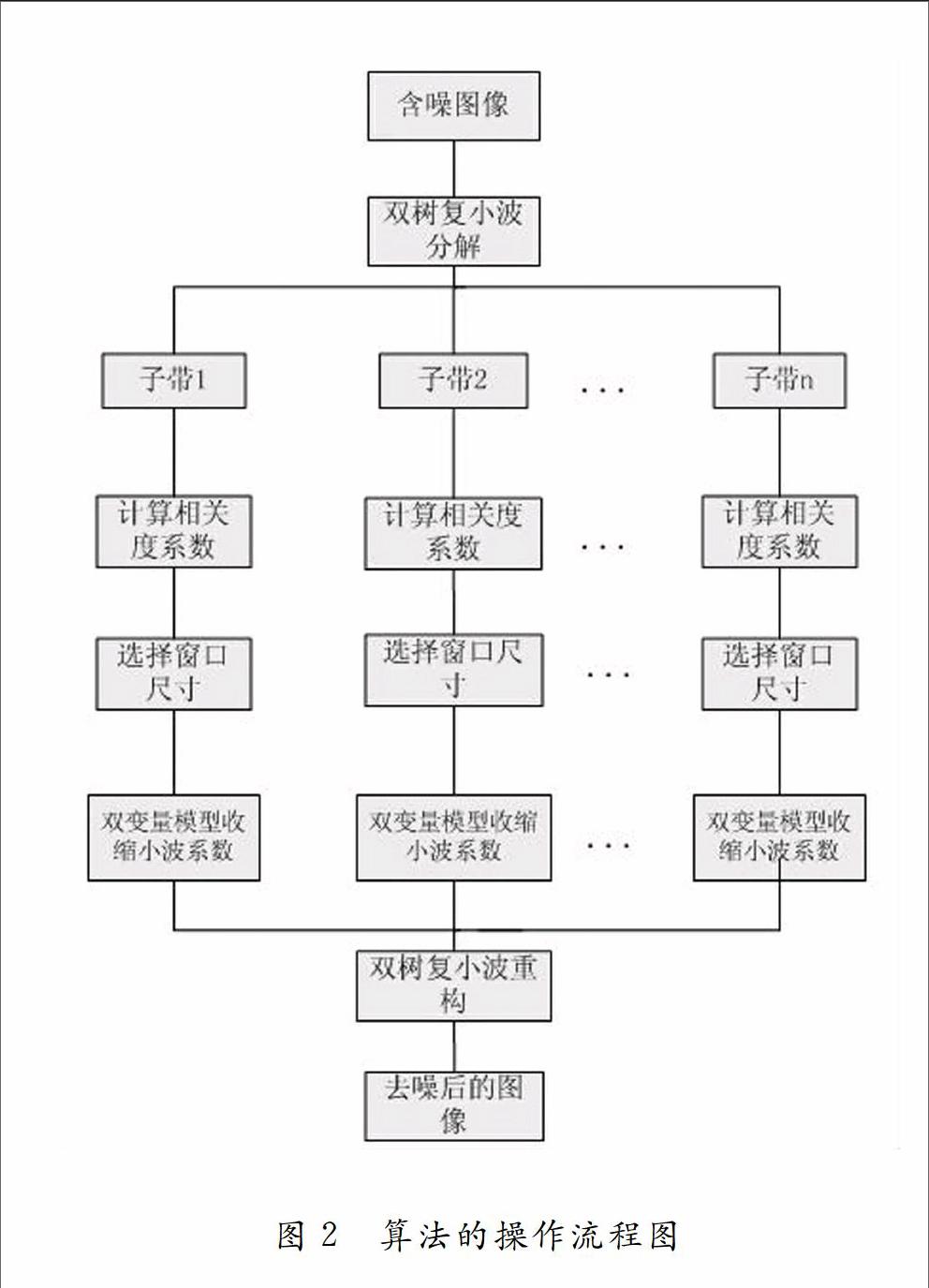
基于双树复小波变换自适应选取邻域窗口算法具体实现方法只是将双变量模型自适应选取邻域窗口算法中二维离散小波变换分解与重构换成双树复小波变换分解与重构，其他步骤算法相同。双树复小波变换自适应选取邻域窗口图像去噪算法的操作流程如图2所示[19-20]。

3.2实验结果分析

在双变量模型图像去噪算法的研究基础上，将双树复小波变换应用在双变量模型图像去噪算法中，采用自适应选取邻域窗口的改进算法，与离散小波变换的双变量模型图像去噪算法（BivaShrink去噪）和局部固定邻域窗口的双变量模型（BivaShrink自选窗去噪）进行实验仿真结果比对，最后进行结果分析，如图3所示。

采用512*512 Pepper标准测试图像进行matlab仿真分析，为更好地比较本文算法与其它去噪算法，实验中分别加入零均值，标准差为20、25、30、35、40、45、50的高斯白噪声，图像去噪的性能用峰值信噪比PSNR来衡量，表1中 比较了Pepper图像双树复小波自选窗算法与BivaShrink自选窗、BivaShrink去噪算法的峰值信噪比，从表1中可以看到双树复小波自选窗算法的峰值信噪比提高的最大，BivaShrink自选窗的峰值信噪比高于BivaShrink 去噪算法。比较分析去噪效果图后，可以得出改进算法能够很好地消除边缘处的失真，改善视觉效果，同时也提高了图像的峰值信噪比，实验结果证明了改进算法的有效性，得出的结论是双树复小波自选窗图像去噪效果优于BivaShrink自选窗，BivaShrink自选窗优于BivaShrink 去噪算法。

4总结语

图像去噪一直以来都是一个难题，要去除噪声同时又较好地保留原有图像的信息很难。凭借小波变换良好的时频特性，其在图像去噪领域得到国内外学者们越来越多的关注。在详细介绍小波变换基本理论基础上，结合小波系数双变量模型和邻域内小波系数的相关度，改进论证了一种双变量模型自适应选取邻域窗口的去噪算法。由于双树复小波变换不仅有着时频局域特性和多分辨特性，还具有平移不变性和更多方向选择性等优良性质，将双树复小波变换应用在双变量模型图像去噪算法中，采用自适应选取邻域窗口的改进算法。实验结果证明，与传统的离散小波变换相比，双树复小波自选窗图像去噪效果优于BivaShrink自选窗，BivaShrink自选窗优于BivaShrink 去噪算法。

参考文献

[1]朱希安，曹林.小波分析及其在数字图像处理中的应用[M].北京：电子工业出版社，2012.

[2]DONOHO D L，JOHNSTONE I M. Adapting to Unknown Smoothness Via Wavelet Shrinkage[J]. American Statical Assoc，1995，90（432）：1200-1224.

[3]吕俊白，蔡灿辉.一种有效保留图像细节的自适应图像消噪方法[J].计算机应用，2010，30（8）：2077-2079.

[4]PAN Jinfeng，PAN Xuefeng.The Adaptive Bivariate Shrinkage Denoising Method[J].978-0-7695-4225-6/10，IEEE Computer Society，2010.

[5]SENDUR L，SELESNICK W.Bivariate shrinkage functions for waveletbased denoising exploiting interscale dependency[J].IEEE Trans.Image Processing.2002，50（11）：2744-2756.

[6]REKABDAR A，KHAYAT O.Using Bivariate Gaussian Distribution for Image Denoising in the 2-D Complex Wavelet Domain[J].978-1-4244-9708-9/10， IEEE，2010.

[7]刘鑫，贺振华，黄德济.基于双变量收缩函数的局域自适应图像去噪[J].计算机应用，2006，26.

[8]董雪燕，郑永果.具有自适应窗口的双变量模型图像去噪方法[J]. 计算机应用与软件，2012，（6）：135-136.

[9]侯建华.基于小波及其统计特性的图像去噪方法研究[D].武汉：华中科技大学，2007.

[10]汤辉.基于小波及其统计模型的图像去噪研究[D].昆明：昆明理工大学，2014.

[11]李江涛，倪国强，王强.基于双树复数小波变换和双变量萎缩阈值图像降噪[J].光学技术，2007，33（5）.

[12]张汗灵，熊先越.基于复小波变换与层间模型的图像去噪[J].光电工程，2006，33（11）.

[13]KINGSBURY N G.Image Processing with the complex wavelet[D].Phil.Trans Royal Society London A September，1999.

[14]REKABDAR A，KHAYAT O.Using Bivariate Gaussian Distribution for Image Denoising in the 2-D Complex Wavelet Domain[J].978-1-4244-9708-9/10， IEEE，2010.

[15]張稳稳.双树复小波域的邻域自适应贝叶斯收缩去噪[J].计算机工程与应用，2012，48（31）.

[16]罗鹏，高协平.基于双树复数小波变换的图像去噪方法[J].光子学报，2008，37（3）：604-608.

[17]刘蕾.基于双树复小波变换的图像去噪[D].北京：北京化工大学，2010.

[18]殷明，白瑞峰，邢燕，等.基于非下采样双树复小波域的双变量模型去噪算法[J].光子学报，2014， 43（10）：131-137.

[19]龚卫国，刘晓营，李伟红，等.双密度双树复小波变换的局域自适应图像去噪[J].光学精密工程，2009，17（5）：1171-1180.

[20]高洪玉，裴连群.双树复小波域农业图像改进半软半硬阈值函数去噪[J].江苏农业科学，2015，（9）：450-452.

第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36，No1Mar. 2 0 1 7第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36，No1Mar. 2 0 1 7

2.1双变量模型

假设图像是含有加性高斯白噪声，方差是σ2n，即有：