考虑冻土与结构相互作用的梯形渠道冻胀破坏弹性地基梁模型

肖 旻 ，王正中，3，刘铨鸿，王 羿 ，葛建锐 ，王兴威

（1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.西北农林科技大学 旱区寒区水工程安全研究中心，陕西 杨凌 712100；3.中国科学院 寒区旱区环境与工程研究所 冻土工程国家重点实验室，甘肃 兰州 730000）

1 研究背景

在北方广大季节性冻土区，衬砌渠道在冬季经常遭受严重的冻胀破坏。随着中国北方各大灌区续建配套、节水改造工程和长距离跨流域调水工程的持续推进，对寒区输水渠道抗冻胀设计方法和防冻胀措施进行深入、系统的研究迫在眉睫。近年来，众多学者对冻土冻胀特征和寒区工程的冻胀破坏机理进行了广泛的理论和试验研究［1-4］。就衬砌渠道而言，王正中等［5-6］对现浇梯形、弧底梯形渠道，申向东等［7］对预制混凝土衬砌梯形渠道，宋玲等［8］对冬季输水条件下的梯形渠道进行了冻胀破坏力学分析。此外，对衬砌渠道冻胀破坏过程的有限元分析等数值模拟方法［9-12］也已有所发展，但因考虑的影响因素较多，过程繁复且计算复杂，工程实践中仍然需要更加方便、简捷的设计方法。

由于渠道衬砌的冻胀在春季具有融沉复位能力，渠系工程抗冻胀设计规范（SL23-2006）［13］指出，在渠道工程设计中可以允许衬砌产生一定的冻胀位移，以达到削减冻胀、降低造价的目的，并以不产生残余位移和累积冻胀为依据给出了冻胀位移允许值，但规范中并没有提供相应的衬砌冻胀变形计算方法。因此，有必要对衬砌冻胀变形及由此引起的冻胀力释放和削减进行定量研究。相对其他抗冻胀设计指标而言，衬砌冻胀位移便于观测且易于控制，因此也有必要建立以衬砌冻胀位移计算（即挠度计算）为基础的衬砌冻胀内力计算方法和冻胀破坏判断准则。

弹性地基梁模型因其可以较好地反映地基与结构间的相互作用［14-16］，已在各类冻土工程结构的力学分析中得到应用。Selvadural等［17］基于弹性地基梁模型分析了地埋管道冻胀破坏诱发机制及其与冻土间的相互作用；Rajani等［18］结合Winkler地基梁模型研究了不均匀冻胀条件下地埋管道对基土冻胀的响应；李方政［19-20］把多管冻结引起的土体冻胀视为正态分布的叠加，应用弹性地基梁模型研究冻土与地铁站底板、隧道支撑管片间的相互作用。但目前涉及寒区混凝土衬砌渠道冻胀破坏的类似研究仍较少见。

该文首先提出一种考虑冻土与结构相互作用的开放系统渠道衬砌冻胀力分布计算方法。基于弹性地基梁理论，通过引入与冻胀变形成比例的附加荷载项导出冻土地基梁的挠曲线微分方程。对现浇梯形渠道底板和坡板分别建立模型并求解，得到挠度、弯矩和剪力的解析表达式，进而建立了基于衬砌冻胀位移计算的渠道衬砌冻胀破坏判断准则。

2 考虑冻土与结构相互作用的渠道衬砌冻胀力分布的计算

冻土与结构间的相互作用包括两个互相耦合的过程：冻土冻胀受到结构约束对结构施加冻胀力荷载；随之产生的结构冻胀变形使其对冻土冻胀的约束程度降低，表现为冻胀力荷载的释放和削减。两个过程相互影响最终达到平衡，此时衬砌板的挠度曲线为渠道衬砌冻胀变形的实际挠度曲线，由此可得渠道衬砌冻胀位移分布规律。本文通过建立并求解梁的挠曲线微分方程来寻求冻土地基梁的实际挠度曲线，建立方程之前需先对冻胀力分布进行计算。

2.1 基本约定和假设由于地下水埋藏较浅导致基土冻结过程中存在明显水分补给（暂不考虑侧向水分补给的情形）的渠道称为开放系统衬砌渠道［1-2］。由于冻土物理力学性质和水分迁移、相变的复杂性，衬砌结构实际受力情况很难精确计算，且考虑因素太多难以求解。本文主要针对开放系统衬砌渠道进行分析，即对特定气象、土质条件下的特定地区，地下水的迁移和补给视为引起衬砌各点冻胀强度差异的主导因素［21］。

图1 梯形混凝土衬砌渠道断面示意图

结合已有研究和工程实践经验，补充如下约定和假设［5-8，22］：

（1）衬砌渠道纵向尺寸远大于横向尺寸，渠道衬砌冻胀破坏力学分析简化为二维平面应变问题。

（2）由于冬季漫长，渠道基土冻结速率缓慢，衬砌冻胀破坏过程视为准静态过程。冻胀破坏过程中冻土和衬砌始终处于变形协调的平衡状态，结构破坏时则处于极限平衡状态。

（3）渠道衬砌结构的形变均在线弹性范围内，略去微小塑性变形，可应用迭加原理。

（4）把渠基冻土视为服从Winkler假设的弹性地基［19-21］，即衬砌各点冻胀力大小仅由各点对应处基土力学特性和冻胀强度决定。又由于冻土冻胀的正交各向异性［23-25］，冻土冻胀变形主要发生在沿热流方向，即垂直于坡板方向。基于此，可将冻土视为预压缩的Winkler弹簧（如图1），其反映了冻土与结构间的相互作用。目前已有研究通过引入弹性薄层单元、离散弹簧单元［26-27］或预压缩体应变［25，28］等进行冻土冻胀数值模拟和力学分析，结果与实测符合较好。

（5）冻胀力计算仅考虑冻结深度范围内冻土的变形，不考虑冻结深度以外未冻土的固结变形。

2.2 渠道基土的自由冻胀量对特定地区的开放系统渠道而言，气象、土质等其他影响因素相似，加之地下水埋深浅，地下水补给强度是决定断面各点冻胀强度的主要因素。中国北部如新疆、甘肃、内蒙古等大部分省区的水利、道路部门都设置大型现场冻胀试验场，实地观测地下水埋深对各类土质基土冻胀强度的影响［1］。大量文献和试验研究表明［1，10，22，29-33］，冻土冻胀强度（即冻胀率）与地下水埋深间呈如下负指数关系：

式中：η0为自由冻胀强度；z为计算点至地下水位的距离，cm；a、b为与当地气象、土质条件有关的经验系数，可由试验数据用最小二乘法拟合。虽然相关试验多针对垂直于地表的土体冻胀，但有研究表明［1，10，31-33］，梯形混凝土衬砌渠道渠基冻土的冻胀也遵循类似规律。

由于渠道断面各点至地下水位的距离不同，依式（1）可得各点对应的基土自由冻胀量ω0(x)如下：

式中：ω0(x)为断面各点的自由冻胀量，cm；η0(x)为断面各点的自由冻胀强度；z(x)为断面各点至地下水位的距离，cm；H为冻结深度，cm；x为计算点的坐标，cm。

由式（2）可知，对开放系统下的基土冻胀，距离地下水位越近处的冻土冻胀强度越大且分布越不均匀；距离地下水位越远处的基土冻胀强度较小且趋于均匀分布。这符合在工程实际中观测到的基本变化趋势［34-35］。

2.3 考虑冻土与结构相互作用的衬砌冻胀力计算为了反映冻土与衬砌结构间的相互作用，设想渠基冻土的自由冻胀被完全约束即衬砌处于未变形的初始状态时，Winkler弹簧处于受约束的预压缩状态，此时衬砌所受冻胀力视为初始外荷载；此后由于衬砌发生冻胀变形使其对冻土的约束程度减小，引起冻胀力的释放和削减，可认为产生一个与衬砌冻胀位移成比例的附加荷载使冻胀力减小；最终冻土和结构间相互作用趋于平衡，此时的荷载分布为实际的冻胀力分布。

当渠道断面某点基土自由冻胀量被完全约束，即被约束的冻胀量为ω0时，又压缩前该点对应的土柱微元体（如图1，为更加直观将其竖直放置）总长为ω0+H，由基本假设（4）、（5），衬砌各点初始冻胀荷载分布可由下式计算：

式中：p(x)为自由冻胀量被完全约束时衬砌所受冻胀力，即初始冻胀荷载，MPa；Ef为冻土弹性模量，MPa。

由于ω0相对H较小，木下诚一提出冻胀力与冻胀强度的线性关系［1，37-38］，由此可把式（3）简化如下：

当基土冻结深度H为1 m，自由冻胀量ω0为2 cm时，采用式（4）计算的相对误差为2%。

工程实践中，由于衬砌的冻胀变形，自由冻胀量往往不会被完全约束，衬砌各点实际被约束的冻胀量为与式（4）类似，衬砌各点实际冻胀力分布可由下式计算：

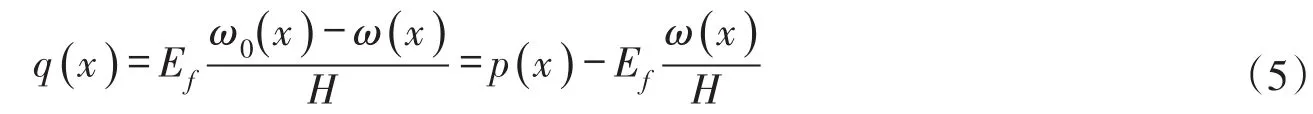
式中：q(x)为衬砌各点实际受到的冻胀力，MPa；ω(x)为断面各点实际的法向冻胀位移（即挠度），cm。等号右侧第一项p(x)为自由冻胀量被完全约束时冻土对衬砌施加的冻胀力，即初始外荷载；第二项为反映衬砌冻胀变形引起冻胀力释放和削减的附加荷载，体现了衬砌结构对冻土冻胀的反作用，该荷载与断面各点实际的冻胀位移成比例。从而式（5）反映了渠基冻土与衬砌结构间的相互作用。

3 渠道衬砌冻胀变形的挠曲线微分方程

3.1 渠道衬砌冻胀变形的挠曲线微分方程基于Winkler假设的弹性地基梁挠曲线微分方程是在一般的梁挠曲线微分方程中引入由地基变形导致的附加荷载项，使其能应用于地基梁变形计算［14-16］。在地基沉降问题中，通常引入与地基沉降变形成比例的附加荷载来反映地基沉降变形导致的地基约束反力。类似地，在地基冻胀问题中，也引入与地基冻胀变形成比例的附加荷载项(Ef/H)⋅ω来反映地基冻胀变形导致的冻胀力的释放和削减，其中比例系数k=Ef/H可相应地视为地基系数［38］。

采用图2、图3所示的坐标系，以向上为正，则基于Winkler模型的弹性地基梁方程如下［19-20，38］：

式中：EI为地基梁的弯曲刚度；ω(x)为冻土与地基梁相互作用的法向位移（即挠度），cm；k为地基系数；p0(x)为作用在地基梁上分布荷载集度，MPa。

本文变量当下标i为1时代表渠底，i为2时则代表渠坡。就梯形衬砌渠道而言，结合式（3）—（6），得渠道衬砌冻胀变形的挠曲线微分方程如下：

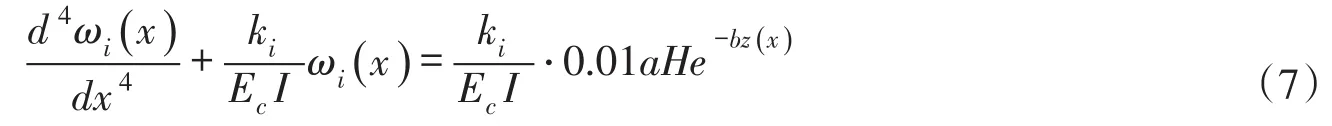
式中：Ec为混凝土弹性模量，MPa；ωi(x)为断面各点实际冻胀位移，cm；ki=Efi/H可视为冻土地基梁的地基系数。

整理式（7）使其化为标准形式如下：

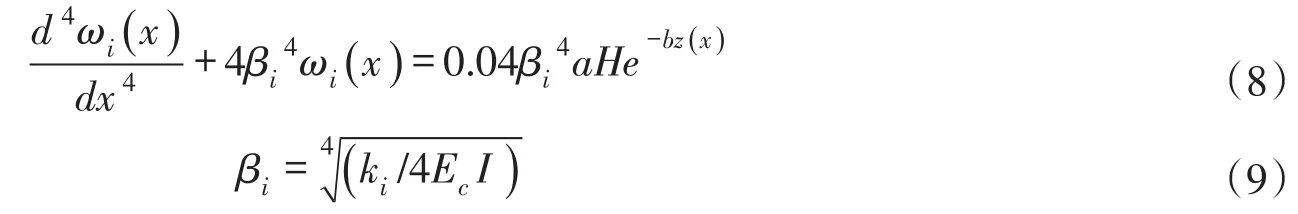
以下针对开放系统梯形混凝土衬砌渠道底板和坡板分别导出微分方程的具体形式。

3.2 梯形渠道底板冻胀变形的挠曲线微分方程梯形渠道底板两端受坡板约束，依据参考文献［5-8，22］把支承方式视为简支，计算简图如图2，其中l1为渠道底板长度，b1为底板厚度。冻胀力作用下视衬砌板为薄板结构，未考虑重力作用，这是偏安全的。反映冻胀力释放和削减的附加荷载项由于分布规律待定没有在图中绘出，其方向为负向，下同。

由于各点至地下水位的距离相同，作用在渠道底板上的初始冻胀荷载p1(x)为均布荷载，从而式（8）右侧为常数。由图1可知z(x)恒等于(z0-h)，代入后得梯形渠道底板冻胀变形的挠曲线微分方程如下：

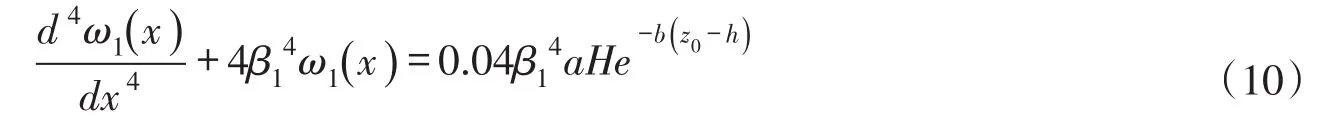
式中：z0为渠道顶部至地下水位的距离，cm；h为渠道断面深度，cm。

图2 渠道底板受力计算简图

图3 渠道坡板受力计算简图

3.3 梯形渠道坡板冻胀变形的挠曲线微分方程渠道坡顶由于冻土与衬砌界面的冻粘作用［39-40］而受法向冻结约束，且开放系统渠道由于水分迁移和地下水补给使该作用更加显著，而同时还在坡脚处受底板的约束。基于此，结合参考文献［5-8，22］可把坡板视为简支梁，计算简图如图3，其中l2为坡板长度，b2为坡板厚度。

梯形渠道坡板各点至地下水位的距离不同，作用在渠道坡板上的初始冻胀荷载p2(x)可由式（4）及几何关系导出。如图1，由几何关系有下式成立：

把式（11）代入式（8）得梯形渠道坡板冻胀变形的挠曲线微分方程如下：

4 挠曲线微分方程的求解

4.1 渠道底板冻胀变形的挠曲线微分方程求解渠道底板冻胀变形的挠曲线微分方程即式（10）为四阶非齐次线性微分方程，其通解由两部分组成：齐次解和特解。其中齐次解如下式所示［38］：

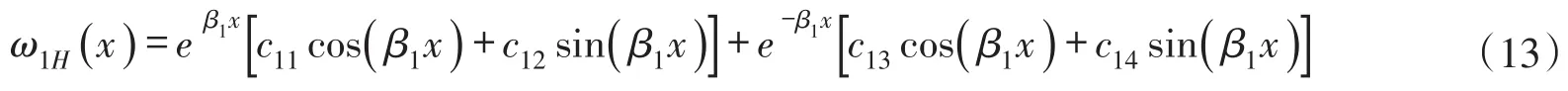
式中：c11、c12、c13、c14为任意常数；β1为特征系数。

此外，式（10）还存在一个特解如下：

代入式（10）可检验解的正确性。结合特解和齐次解，可得通解如下：

在式（15）中应用上述边界条件可得联立方程组如下：

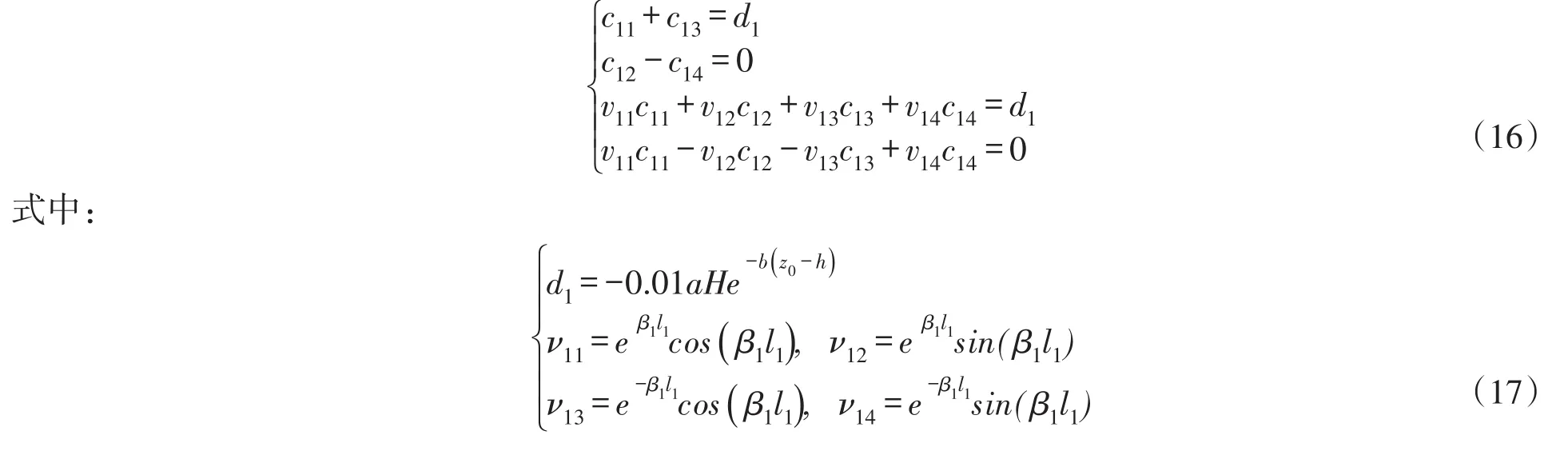
对各参数均为已知的具体衬砌渠道，式（17）中各项均可算出，代入可解出4个任意常数，则原方程得解。

4.2 渠道坡板冻胀变形的挠曲线微分方程求解坡板冻胀变形的挠曲线微分方程即式（12）也是四阶非齐次线性微分方程，齐次解的形式与式（13）一致。

由比较系数法可得式（12）存在特解如下：

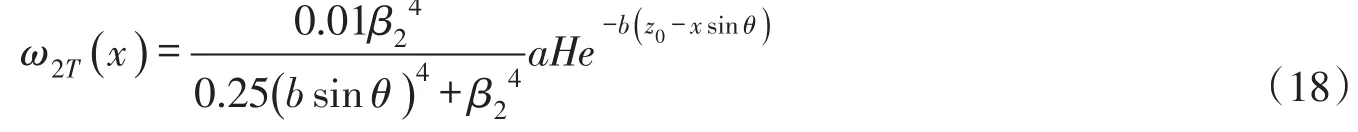
代入式（12）可检验解的正确性。结合特解和齐次解，可得式（12）的通解如下：

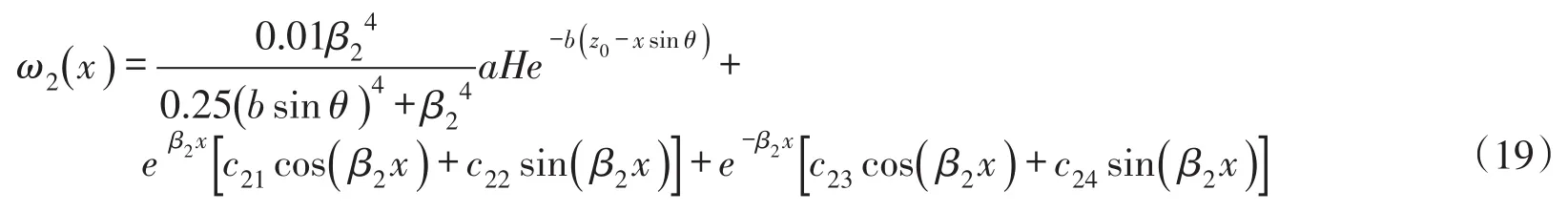
式中：c21、c22、c23、c24为任意常数；β2为特征系数。

在式（19）中应用上述边界条件可得联立方程组如下：

对参数已知的具体衬砌渠道，式（21）中各项均可算出，代入可解出4个任意常数，则原方程得解。

5 内力计算和冻胀破坏判断准则

由梯形渠道坡板和底板冻胀位移的解析表达式即式（15）、式（19）可以分别导出坡板和底板的内力计算公式，进而建立冻胀破坏的判断准则。

5.1 梯形渠道衬砌冻胀内力计算渠道底板采用如图2所示坐标系，坡板采用如图3所示坐标系。由小变形假设即假设（3），轴向拉力大小不受衬砌挠度影响，轴向拉力N（x）可仍按已有文献［5-8，22］的相关方法计算。

截面弯矩沿断面的分布规律如下：

式中：当i=1时，和分别为底板各截面的弯矩和挠度；当i=2时，和分别为坡板各截面的弯矩和挠度，下同。由于坐标系y轴正方向朝上，故该式右侧为正。

衬砌截面剪力沿断面的分布规律可通过对上式求导获得，即：

式中：Pi(x)为衬砌各点对应截面的剪力，MPa。

与已有研究［5-8，22］相店埠河水体不存在明显的微生物反硝化作用比，以衬砌冻胀位移计算即挠度计算为基础的冻胀内力计算公式更加简洁，且可对坡板和底板内力建立统一的计算公式。现以渠道底板为例分别写出式（22）、式（23）的具体形式如下：

5.2 梯形渠道衬砌冻胀破坏判断准则结合笔者对塔里木灌区渠道冻胀破坏状况的调查发现［35］，渠道衬砌冻胀位移过大是导致衬砌板鼓胀和隆起的主要原因。若还由于局部弯矩过大导致强度破坏，则将使渠道衬砌板产生裂缝甚至折断。此外，渠道衬砌冻胀位移过大还可能影响衬砌结构的稳定性，导致架空乃至滑塌。

混凝土衬砌材料抗拉强度较低，衬砌板常因局部弯矩过大导致截面拉应力达到抗拉极限而开裂，这一方面降低了衬砌板的抗弯刚度，另一方面则导致渗漏增强使衬砌板的冻胀破坏加剧；随后冻胀-融沉的周期变化使衬砌渠道进入“冻胀开裂-渗漏增强-冻胀破坏加剧”的恶性循环中，并使裂缝进一步扩展直至贯通而最终导致衬砌彻底破坏。由此可见，截面拉应力达到材料抗拉极限引起衬砌开裂是衬砌渠道进入恶性循环，并最终彻底破坏的触发标志。这与高强度钢在低应力水平反复作用下发生渐进式疲劳破坏的机理不同。因此，可以通过控制裂缝的产生来避免衬砌板的冻胀破坏，即通过对渠道衬砌最易破坏截面进行抗裂验算来建立冻胀破坏的判断准则。计算公式如下：

式中：σmax为截面最大拉应力；当i=1时，和bi分别为底板各点对应截面的轴力和底板厚度；当i=2时，Ni(x)和bi分别为坡板各点对应截面的轴力和坡板厚度；[ε]为允许产生的拉应变。

为避免渠道衬砌冻胀位移过大导致衬砌板鼓胀、隆起甚至架空、滑塌，规范［13］以衬砌允许法向位移值作为衬砌冻胀变形和抗冻胀稳定性的控制指标，即：

式中：[Δh]为允许法向位移值，可依据规范取值。

6 工程算例

6.1 研究区域与工程概况新疆塔里木灌区以阿拉尔市为中心［34-35］，年最低气温-24℃～-29.3℃，已修建渠道2 355 km，地表水丰沛，有塔里木河、阿克苏新大河、和田河等五大河流贯穿，地下水为河流两岸嵌入式淡水体，地下水埋深较浅，渠道衬砌存在严重冻胀破坏。由于此类旱寒地区雨量稀少且地下水埋深浅，引发基土冻胀的主要水分来源是地下水补给。

图4为新疆塔里木灌区某梯形渠道断面示意图（以一侧坡板为例）。该渠道为C15混凝土衬砌，板厚为8 cm，渠坡和渠底的冻土层冬季最低温度分别为-14.7℃和-9.4℃。本例中冻土弹性模量按冬季冻土层最低温度取值，这是偏安全的。渠道基土冻结深度约为1 m，地下水埋深z0为3.5 m，坡板倾角为45°，渠道基土土质为轻壤土。笔者于2010—2011年越冬期对其进行了原型观测［35］，底板间隔25 cm设一个测点；由于坡板较长且不便观测，故间隔50 cm设一个测点。现对衬砌各点冻胀位移进行计算及对比分析。相关参数与经验系数见表1。

图4 原型渠道断面示意图

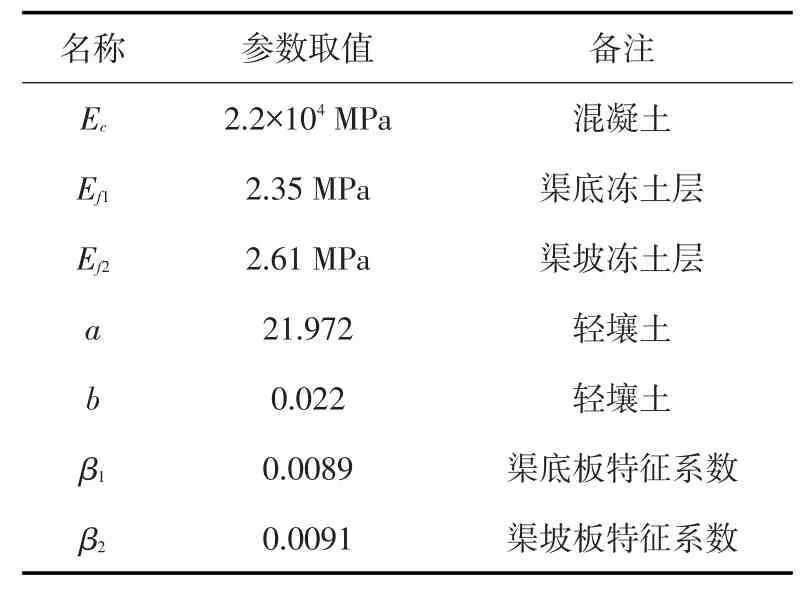
表1 相关参数与经验系数［1，22，31］

6.2 衬砌冻胀位移的计算与对比分析根据如式（16）所示的联立方程组可解得任意常数：c11=1.024，c12=-0.23，c13=-3.453，c14=-0.23；分别代入式（15）可得渠道底板各点法向冻胀位移（即挠度）的解析表达式，其函数图像如图5。类似地，求解如式（20）所示的方程组可得任意常数：c21=-0.053，c22=0.203，c23=0.05，c24=0.203；分别代入式（19）可得渠道坡板各点挠度的解析表达式，其函数图像如图6。此外，由材料力学方法即挠曲线微分方程中不引入反映冻胀力释放和削减的附加荷载项，也可分别对渠道底板和坡板各点挠度进行求解。图5、图6为采用本文方法、材料力学方法的计算结果与观测值的对比图。

如图5、图6中所示，本文方法由于考虑衬砌冻胀变形引起的冻胀力削减和释放，冻胀位移计算结果均较材料力学方法小，且与观测值更加符合。渠道底板各点位移表现为中间大、两边小的分布特征；坡板各点冻胀位移则表现为中下部较大，上部较小的分布特征，这与工程实际基本相符。本文计算值与观测值相比仍显偏大，这是因为衬砌结构被视为薄板结构，未考虑重力，这是偏安全的；渠道坡板和底板两端的观测值并非准确地为零，即把衬砌板视为简支梁结构的计算结果与观测值也存在一定偏差，但偏差不显著。

6.3 衬砌冻胀变形及稳定性验算由图5、图6还可以发现，无论是渠道坡板还是底板，各点冻胀位移通常都存在一个峰值，该值所在截面附近最可能发生拉裂和折断等冻胀破坏，由此可见对最易破坏截面所在位置和冻胀变形的估算具有重要的实际意义。渠道底板各点冻胀位移最大值所在截面为中间截面，且有ω1max=ω1(1 0 0)=2.217cm，表明中间截面是渠道底板最易发生冻胀破坏的位置。

图5 渠道底板冻胀位移曲线

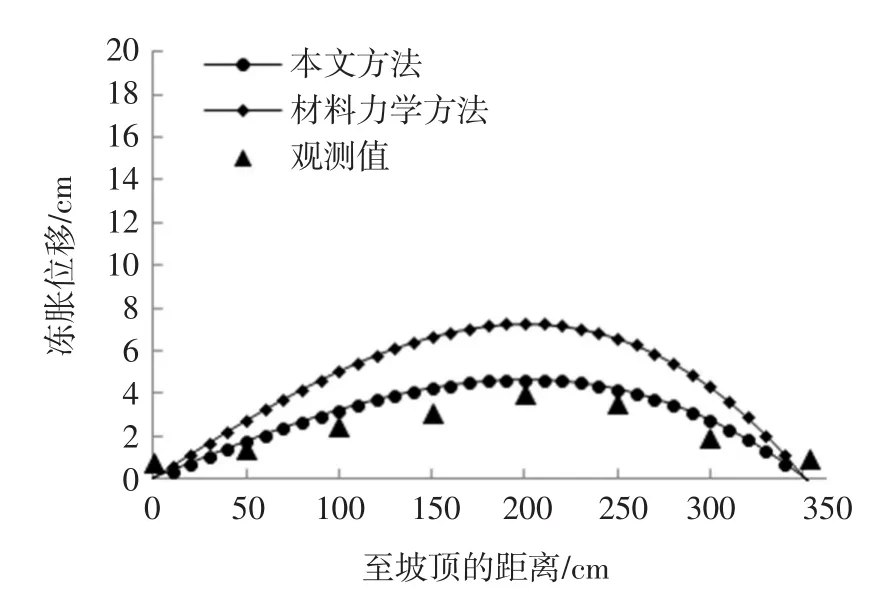
图6 渠道坡板冻胀位移曲线

坡板各点冻胀位移最大值所在截面可通过求式（19）中导数为零的点来选取。令ω′2(x)=0，采用二分法求根，预定精度为0.005，二分9次后得该截面在距离坡顶199.94 cm处，即距离坡顶约62.32%处，且有ω2max=ω2(1 00)=4.637cm。笔者对塔里木灌区渠道冻胀破坏状况的调查结果表明，梯形渠道衬砌破坏主要发生在距离坡顶55%～75%坡板长处；已有研究结果也一般认为坡板最易破坏截面在距渠顶约2/3坡板长处，均与本文估算结果基本相符。此外，由以上分析结果可见渠道坡板和底板最易破坏截面冻胀位移计算值均大于允许值（衬砌允许法向位移值为2 cm［13］），表明渠道衬砌存在发生冻胀破坏的可能。据调查，渠道在该越冬期内确实有部分渠段发生冻胀破坏，表明计算结果与实地调查结果也基本相符。

6.4 不同地下水位对衬砌冻胀位移的影响为了分析开放系统梯形渠道在不同地下水位（至渠顶）时衬砌板的冻胀位移特征，仍以该渠道为原型，假定渠顶地下水位分别为3、3.5、4、4.5和5 m时分别对渠道底板和坡板的冻胀位移进行计算，计算结果如图7、图8。由图可知，不同渠顶地下水埋深对衬砌板冻胀位移的总体趋势影响较小，但对断面各点冻胀位移的大小尤其是最大冻胀位移的量值影响显著。随着地下水埋深越浅，衬砌冻胀位移迅速增大。这表明寒区高地下水位渠道极易发生冻胀破坏，这与事实相符。

7 结论与讨论

该文提出一种考虑冻土与结构相互作用的开放系统渠道衬砌冻胀力分布计算方法，基于弹性地基梁理论建立了开放系统梯形渠道衬砌的冻胀破坏力学分析模型和冻胀破坏判断准则。获得如下结论：（1）对冻胀力均布的梯形渠道底板和冻胀力非均布的渠道坡板分别导出挠曲线微分方程并求解，得相应挠度、弯矩和剪力的解析表达式，同时也表明本文方法对均布和非均布冻胀荷载具有良好的通用性和适应性；（2）以塔里木灌区某梯形渠道为原型计算衬砌各点冻胀位移，并与材料力学方法及原型观测值进行了对比分析。结果表明，由于材料力学方法仅考虑静力平衡条件而没有考虑渠基冻土冻胀时与渠道衬砌的协调变形，计算结果与观测值存在较大偏差。本文方法由于考虑了渠基冻土与衬砌协调变形引起的冻胀力释放和削减，计算结果均较材料力学方法小，且与观测值更加符合；（3）对开放系统梯形渠道在不同地下水埋深时的衬砌冻胀位移进行对比分析，结果表明不同地下水埋深对衬砌板冻胀位移的总体变化趋势影响较小，但对各点冻胀位移的大小尤其是最大冻胀位移的量值影响显著。随地下水埋深越浅衬砌冻胀位移迅速增大，表明寒区高地下水位渠道衬砌极易发生冻胀破坏，这与事实相符。

图7 不同地下水位渠道底板冻胀位移曲线

图8 不同地下水位渠道坡板冻胀位移曲线

实际上，即使同一地区气象、土质条件相似，断面各点除地下水补给强度外，太阳辐射强度差异对基土冻胀强度的影响通常也需加以考虑。综合考虑地下水补给和太阳辐射差异的模型有待进一步的深入研究。

参 考 文 献：

［1］ 陈肖柏，刘建坤，刘鸿绪，等.土的冻结作用与地基［M］.北京：科学出版社，2006.

［2］ 马巍，王大雁.冻土力学［M］.北京：科学出版社，2014.

［3］ 蔡正银，张晨，黄英豪，等.冻土离心模拟技术研究进展［J］.水利学报，2017，48（4）：398-407.

［4］ 周家作，韦昌富，李东庆，等.饱和粉土冻胀试验研究及数值模拟［J］.岩石力学与工程学报，2017，36（2）：485-495.

［5］ 王正中.梯形渠道砼衬砌冻胀破坏的力学模型研究［J］.农业工程学报，2004，20（3）：24-29.

［6］ 王正中，李甲林，陈涛，等.弧底梯形渠道砼衬砌冻胀破坏的力学模型研究［J］.农业工程学报，2008，24（1）：18-23.

［7］ 申向东，郑玉佩，王丽萍.混凝土预制板衬砌梯形断面渠道的冻胀破坏受力分析［J］.农业工程学报，2012，28（16）：80-85.

［8］ 宋玲，欧阳辉，余书超.混凝土防渗渠道冬季输水运行中冻胀与抗冻胀力验算［J］.农业工程学报，2015，31（18）：114-120.

［9］ 李学军，费良军，任之忠.大型U型渠道渠基季节性冻融水分运移特性研究［J］.水利学报，2007，38（11）：1383-1387.

［10］ 安鹏，邢义川，张爱军.基于部分保温法的渠道保温板厚度计算与数值模拟［J］.农业工程学报，2013，29（17）：54-62.

［11］ 李爽，王正中，高兰兰，等.考虑混凝土衬砌板与冻土接触非线性的渠道冻胀数值模拟［J］.水利学报，2014，45（4）：497-503.

［12］ LI Zhuo，LIU Sihong，FENG Youting，et al.Numerical study on the effect of frost heave prevention with different canal lining structure in seasonally frozen ground regions［J］.Cold Regions Science and Technology，2013，85（1）：242-249.

［13］ SL23-2006.渠系工程抗冻胀设计规范［S］.北京：中国水利水电出版社，2006.

［14］ SELVADURAL A P S.Elastic Analysis of Soil-foundation Interaction［M］.NewYork：Elsevier Scientific Publish⁃ing Company，1979.

［15］ 黄义，何芳社.弹性地基上的梁、板、壳［M］.北京：科学出版社，2005.

［16］ 赵明华，马缤辉，罗松南.考虑底面摩阻效应的弹性地基梁微分算子级数法［J］.水利学报，2011，42（4）：469-476.

［17］ SELVADURAL A P S，SHINDE S B.Frost heave induced mechanics of buried pipelines［J］.Journal of Geotech⁃nical Engineering，ASCE，1993，119（12）：1929-1952.

［18］ RAJANI B，MORGENSTERN N.Comparison of predicted and observed response of pipeline to differential frost heave［J］.Canada Geotechnical Journal，1994，31（6）：803-816.

［19］ 李方政.土体冻胀与地基梁相互作用的叠加法研究［J］.岩土力学，2009，30（1）：79-85.

［20］ 李方政.冻土帷幕与结构相互作用的冻胀和蠕变效应与应用研究［D］.南京：东南大学，2005.

［21］ 肖旻，王正中，刘铨鸿，等.开放系统预制混凝土梯形渠道冻胀破坏力学模型及验证［J］.农业工程学报，2016，32（19）：100-105.

［22］ 李甲林，王正中.渠道衬砌冻胀破坏力学模型及防冻胀结构［M］.北京：中国水利水电出版社，2013.

［23］ 王正中，沙际德，蒋允静，等.正交各向异性冻土与建筑物相互作用的非线性有限元分析［J］.土木工程学报，1999，32（3）：55-60.

［24］ 王正中，袁驷，陈涛，等.冻土横观各向同性非线性本构模型的实验研究［J］.岩土工程学报，2007，29（8）：1215-1218.

［25］ 蔡海兵，程桦，姚直书，等.基于冻土正交各向异性冻胀变形的隧道冻结期地层位移数值分析［J］.岩石力学与工程学报，2015，34（8）：485-495.

［26］ 李方政.基于蠕变效应的穿越隧道冻结帷幕开挖与支护三维数值模拟［J］.岩土力学，2005，26（S1）：121-132.

［27］ 郭红雨，贾艳敏.用能量法确定考虑冻胀力和冻土抗力作用时桩基的临界荷载［J］.工程力学，2007，24（7）：167-173.

［28］ 蔡海兵.地铁隧道水平冻结工程地层冻胀融沉的预测方法及工程应用［D］.长沙：中南大学，2012.

［29］ 盛岱超，张升，贺佐跃.土体冻胀敏感性评价［J］.岩石力学与工程学报，2014，33（3）：594-605.

［30］ 田亚护.动、静荷载作用下细粒土冻结时水分迁移与冻胀特性实验研究［D］.北京：北京交通大学，2008.

［31］ 李安国，李浩，陈清华.渠道基土冻胀预报的研究［J］.西北水资源与水工程学报，1993，4（3）：17-23.

［32］ 山西省渠道防渗工程技术手册编委会.山西省渠道防渗工程技术手册［M］.太原：山西科技出版社，2003.

［33］ 朱强，付思宁，武福学，等.论季节冻土的冻胀沿冻深分布［J］.冰川冻土，1988，10（1）：1-7.

［34］ 塔里木灌区水利管理处史志编撰委员会.塔里木灌区水利管理处志［M］.乌鲁木齐：新疆人民出版社，2001.

［35］ 肖旻.塔里木灌区防渗渠道破坏机理及综合防治措施研究［D］.阿拉尔：塔里木大学，2011.

［36］ 木下诚一.冻土物理学［M］.王异，张志权，译.长春：吉林科学技术出版社，1985.

［37］ 周长庆.关于法向冻胀力计算方法的讨论［J］.冰川冻土，1981，3（2）：18-23

［38］ 龙驭球.弹性地基梁的计算［M］.北京：人民教育出版社，1981.

［39］ 杨晓东，金敬福.冰的粘附机理与抗冻粘技术进展［J］.长春理工大学学报，2002，25（4）：17-19.

［40］ 丁金波.结冰表面冻粘特性的试验研究［D］.上海：上海交通大学，2012.