白族文化中数学元素的挖掘

杨梦洁，王彭德，杨泽恒



白族文化中数学元素的挖掘

杨梦洁，王彭德，杨泽恒

（大理大学数学与计算机学院，云南大理 671003）

白族的宗教文化、民族服饰、民俗风情、建筑装饰、白族语言等都是白族文化的重要载体，蕴含着丰富的数学元素，对这些载体进行研究，挖掘其中蕴含的数学元素，探析白族文化和数学文化的共通性，有利于白族文化的传承，丰富民族数学的内涵，促进多元文化的健康发展．

宗教文化；民族服饰；民俗风情；白族语言；数学元素

中国少数民族生活中蕴藏着丰富的数学文化，它们主要表现在建筑装饰、风俗习惯、民族服饰、宗教信仰、民族语言等方面．不同的民族因其地理环境和历史发展过程不同而具有不同的数学文化特征，使之成为具有自己特色的文化现象，这些特征为在国内开展民俗数学研究提供了丰富的资源．诸如：在20世纪90年代，内蒙古师范大学代钦教授研究发现蒙古包的建筑结构存在黄金分割比0.618以及蒙古族计算方法体现在古经《珠露海》中[1]；西南民族大学周开瑞教授发现羌族记数工具是一条硬质圆木棍[2]；近年来贵州凯里学院罗永超教授研究发现侗族人民巧妙地运用了2和及10的倍数将乘法转化为加减法的运算[3]；肖绍菊教授研究发现苗族人民崇拜图腾和数字以及苗族图纹中的螺旋美[4]；西南大学朱黎生博士研究发现彝族服饰图案充满了许多的几何变换和镶嵌，并以适当的方式应用到初中数学的教学设计中[5]．这些研究成果正是蒙古族、侗族、苗族、彝族等少数民族聚居在某个固定区域，经过长期的生产和生活形成的数学文化．白族是古老的民族之一，文化丰富多彩，聪慧的白族人民在社会生产实践中不断积累，形成了独特的数学文化．白族建筑、民族服饰、民俗风情、宗教文化等都是白族文化的重要载体，蕴含着丰富的数学元素，如：黄金分割、连续纹样、几何变换、平面镶嵌、弦图等，挖掘这些民族数学资源，既可使白族数学文化得以传承，又可使人们感受到身边的数学，对于丰富数学的内涵、推进少数民族数学课程改革具有一定的实际意义．

鉴于人类学的研究方法，采用田野调查法，深入白族地区，整理民间的素材，挖掘潜藏在白族文化中的数学文化，发现白族人民的数学智慧，通过对白族的宗教文化、民族服饰、建筑装饰、民俗风情、白族语言等载体所蕴含的数学元素进行研究，试图探析白族文化与数学文化的共通性．

1 白族宗教文化中的数学元素

1.1 崇圣三塔寺中的数学元素

崇圣三塔寺（如图1）是苍洱间最具代表性的宗教建筑之一，大塔叫千寻塔，高69.13米，为密檐式正方形空心砖塔，塔身内壁垂直贯通上下，塔顶有四方形瞭望小孔，从小孔可欣赏大理古城的全貌，南北两座小塔高度相同，都是42.19米，各有10层．多年来，很多学者都是从佛学的角度对其进行研究，很少有从数学文化的角度来探讨这一宗教建筑．经过观察研究，可以发现整个三塔建筑群中蕴含着丰富的数学元素．

图1 崇圣寺三塔

①对称：在古代“对称”一词的含义是“和谐”、“美观”，而白族建筑学中也充分利用了对称，使数学与美学完美结合．大理佛教尊金翅鸟为保护神，能慑服诸龙，消除水患．如大理三塔寺前的大鹏金翅鸟雕塑（如图2），是轴对称的图形．崇圣寺三塔，一大二小，左右均衡对称，一高两低，也展现出了数学中的对称美与和谐美．

图2 大鹏金翅鸟

②丰富的几何图形：三塔中，大塔在前，两个小塔紧跟其后，大塔与小塔等间隔70米，两个小塔相距90米，平面上形成了等腰三角形，立体空间上形成三足鼎力之势．大塔有上、中、下3层基座，上台和中台均为八角形，下台为正方形，两个小塔一至八层为空心直壁，八层以上为实心，基底仍为八角形．在中原的一些塔由基座向上直线收缩，下大上小，呈矩梯形，而三塔中的大塔上下较小，中部较大，主视图的外部轮廓呈曲线．

③偶数：大理三塔之所以闻名中外，除了布局、造型统一外，还有与其它塔不同的建造寓意，通常建造的佛塔都为奇数层的塔，如西安大雁塔是七层塔、杭州雷峰塔是九层塔……而大理三塔是偶数塔．那是因为佛教传入大理之后，与白族的本主教相结合，主张男女平等，都修行佛教，所以三塔按偶数层来建造．宗教中数字常常寄托着美好的寓意，而白族人民在数字运用上的独特性，创造出颇具独特的白族数学文化．

④黄金分割：黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值，在很长的一段历史时期里，黄金分割的观点一直统治着西方建筑美学，应用时其比值一般取0.618．同样在白族地区最具代表性的宗教建筑之一崇圣三塔寺也有黄金分割的比例，如大塔高69.13米，两个小塔高都为42.19米，其比值42.19/69.13≈0.61接近黄金分割取值．因此美的建筑一般都与黄金分割比例相关[3]．

⑤射影几何学：射影几何学是专门研究图形的位置关系，也是用来讨论在把点投影到直线或平面上的时候，图形的不变性的科学．如图1三塔的倒影公园内有椭圆形水潭，因能倒影更增添了三塔的魅力．三塔的倒影公园即利用光线的作用，把三维空间的物体投影到水平面上，其图形不变，这样的设计充分展现了射影几何学在三塔的倒影公园建筑构想中的运用．可见白族祖先早已将几何空间思维能力合理投射到三塔建筑上．

1.2 本主文化中的数学元素

本主崇拜是白族特有的一种宗教信仰，白族对本主的信仰几乎是全民性的，白族地区具体有多少本主神祗，至今尚无确切统计数据，民间有“五百神王”之说，但仅仅大理坝区就远远超出了这一数字，由于白族由原来的洱海区域向各地发展的过程中又产生了众多不同的分支，数目更多．在整个洱海地区的全部神祗中，本主具有一定的层次和数量关系．第一层“中央本主”（神中之王）；第二层“九坛神”（九个本主）；第三层“18坛神”（18个本主）；再往下是“72景帝”，即72个本主，然后才是“500神王”，再加上亲眷本主的数目就更为可观了．在清同治年间，天主教传入大理后，大理成为滇西地区天主教传播中心，坐落于大理古城内的天主教堂现今仍保留着神都对联（如图3）：“匾额：护法神宫，上联：名高五百神王护法除魔赫赫威灵垂万世，下联：位尊七二景帝爱民建国巍巍功德懋千秋”[6]．

图3 大理天主教堂对联

2 白族服饰中的数学元素

服饰和衣着穿戴，它不仅仅是一个民族的标志，而且还具有重要的研究价值，从蛮荒岁月到现代文明，白族人民依赖着特色的白族文化逐步发展起与服饰相关的制作工艺及艺术趣味，而数学元素也巧妙地运用在这一件件工艺精湛的“艺术品”中．

2.1 白族服装中的数字

居住在丽江九河的传统白族妇女通常背披七星图案的黑羊皮褂，上面缀着7个图形纹样，称为“七星”，直径长约7厘米．在过去的披肩上面还有两个直径长约12厘米的图形纹样称为“月亮”，象征披星戴月，以示勤劳[7]．

白族人民赋予了服饰数字的象征寓义，如大理鹤庆白族头饰（如图4），坝区甸北姑娘以头顶外罩蓝、紫或黑色的两幅1尺2寸见方的头巾，象征一年12个月，外沿头缠3丈6尺红头绳，象征着一年360天．

图4 白族妇女服饰

2.2 白族刺绣和扎染中的几何元素

白族刺绣是白族妇女手工艺，广泛运用于服饰、头饰、鞋帽等日常生活用品．白族刺绣和扎染图案中存在许多几何元素，由一些简单几何图案利用轴对称、中心对称、平移、旋转等几何变换组成了美丽复杂的纹理图案．

2.2.1 几何变换

（1）轴对称和平移变换：白族刺绣最讲究对称美，上下左右不论图形和空间都完全要求对称，故图案中的纹样很多都具有对称性，有些图案既是轴对称图形，又是中心对称图形，体现了数学的对称美．如白族的围腰上绣着对花、凤凰、飞燕、藤蔓等图形，大多表达对纯真爱情的向往、期待和赞颂．刺绣图案白族少女的挎包（图5）中有一条对称轴；常出现在白族传统服装围腰上的图案（图6），有多条对称轴，长条状的花纹可由“图案单元”平移得到，也可将平移与轴对称结合起来，这种图案有规律的重复，更增添了美感．

图5 白族少女挎包

图6 白族妇女围腰

（2）纹样的连续：连续与离散是数学的重要概念，在民族服饰中也存在连续图案．纹样有连续纹样和适合纹样．连续纹样是根据条理与反复的组织规律，将单位纹样作重复排列，构成无限循环的图案，根据重复的方向不同，分为二方连续和四方连续．两方连续图案广泛应用于白族刺绣图案中，例如象征着大理“风花雪月”的白族包头上的刺绣图案就大量运用了两方连续元素（图7）．四方连续的常见排法有梯形连续、菱形连续和方形连续等，图8的图案中就运用了四方连续．适合纹样是具有一定外形限制的图案纹样、它是将几何素材在限制的图形中进行变化处理，组织在一定的轮廓内，外形为矩形或圆．白族工艺品（图9、10）中的适合纹样，有梯形或圆向外连续．

图7白族妇女包头

图9 适合纹样

图10 白族妇女背包

（3）相似变换和旋转变换

形状相同的图形叫做相似图形．图11中的图案就由两个全等的三角形，拼接成一个与原图形相似的三角形，以此类推可拼接成更大的相似三角形，相似比为1∶．图12中每条鱼绕着某一定点，顺时针或逆时针方向旋转45°后可得到下一条鱼，这样做7次旋转后可得到一个圆环图案，故每相连两条鱼的鱼嘴与圆心红点连线的夹角均为45°．

图11 相似变换图案

图12 旋转变换图案

2.2.2 几何曲线

（1）心形线（如图13）：心形线是一个圆上的固定一点在它绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹，因其形状像心形而得名．相传数学家笛卡尔流浪到瑞典，认识了公主克里斯汀，后成为她的数学老师，两人相处彼此产生爱慕之心，一次笛卡尔给公主的一封信中只有短短的一个公式：，公主看到信后十分激动，马上把方程的图形画出来，就看到一颗心的形状，这就是著名的“心形线”．如图14为白族围腰中的心形图案，常寄托着人们对爱情的永恒美好期待，故白族人民喜爱在服饰的设计上构造心形图案．

图13 心形线

图14 白族围腰

（2）星形线（如图15）：星形线像夜空中光芒四射的星星，因此得名，图16为白族扎染星形图案，星形线方程为．

（3）四叶草曲线（如图17）：四叶草在民间被称为幸运草，一般只有三叶，四叶并不多见，在十万株苜蓿草中，发现四叶草的机率大约是十万分之一，故而能遇上则意味着幸运之神即将降临．因此在白族的扎染有较多的四叶草图案，如图16、18中有着许多的四叶草图案，体现了白族人民对美好生活的一种向往．四叶草曲线极坐标方程为．

图15 星形线

图16 扎染中星形图案

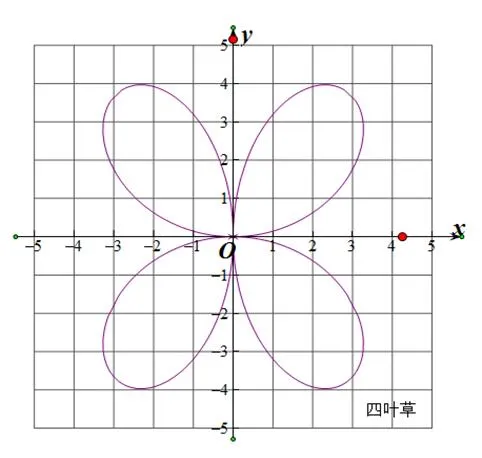
图17 四叶草曲线

图18 四叶草图案

（4）玫瑰线（如图19）：图20为白族扎染的玫瑰图案，玫瑰线的极坐标方程为，如果是偶数，玫瑰线就有2个瓣，如果是奇数，则有个瓣．玫瑰曲线的图像与五彩缤纷的花朵有很大的相似性，能给人美的享受，因此在白族扎染中常见玫瑰图案．

2.3 白族银饰中的几何图案

白族人民以柔为美，对几何图形塑造的美情有独钟，在白族银饰图案上有许多几何图形，如圆、双纽线（如图21）、螺旋线（如图22）、星形线等．经过长期的积累，白族人民将这些最基本的几何图形连接、堆积组合成了复杂的纹样．如白族银饰中的双纽图案（如图23）和阿基米德螺旋图案（如图24）．

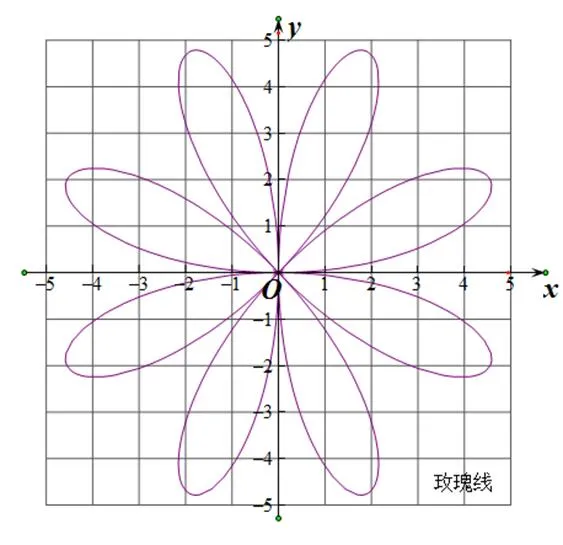
图19 玫瑰线

图20 扎染中的玫瑰图案

图21 双纽线

图22 螺旋线

图23 双纽图案

3 白族建筑装饰中的数学元素

少数民族的建筑装饰艺术是少数民族文化的一种特殊载体，作为物质文化和精神文化的结晶．人们已经对白族民居建筑装饰从美学、艺术、民俗等视角进行研究和解读，但从数学文化视角对白族民居建筑装饰进行研究尚属鲜见．大理白族民居建筑以“三坊一照壁”，“四合五天井”最为常见，建筑风格统一和谐，布局合理有序，很讲究对称，大到整体的布局上对称，每一栋楼房、照壁本身都对称，小到每一个建筑装饰元件．如图25为白族民居山墙的装饰图案——山花，左右对称，使整面墙看起来统一协调．另外每一种图案都有一种寓意，传说中的四叶草的四片叶分别代表名誉、财富、爱情及健康，因此有较多的四叶草图案（如图26）用于白族建筑的各种装饰中．

图25 白族民居山墙装饰图案

图26 白族建筑装饰的四叶草图案

3.1 平面镶嵌

用形状和大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠的图形，即为平面图形的镶嵌．建筑中的镶嵌艺术是构成整个建筑不可或缺的有机组成部分，在白族建筑中，常把平面镶嵌用于建筑装饰中，同种纹案与不同种纹案镶嵌使建筑美感发挥到了极致，给人一种视觉审美的享受．如图27是白族地区常见的墙体壁画，它是用形状、大小相同的正六边形砖块围绕着一个圆形的大理石镶嵌而成的平面图形，由正多边形的内角和公式可计算出正六边形的每个角都为120°，因此可以进行平面镶嵌．云南剑川是全国著名的“木雕之乡”，木雕主要用于建筑物装饰，如图28是白族民居格子门窗，从大的方向看，它是由每一个小正方形外面围着4个大正方形为一单元镶嵌成的一个图形，如图29，它们之间不是杂乱无章的，而是根据一定的比例进行镶嵌的，大正方形的边长是小正方形边长的3倍．

图27 白族民居墙体壁画

图28 白族民居格子门窗

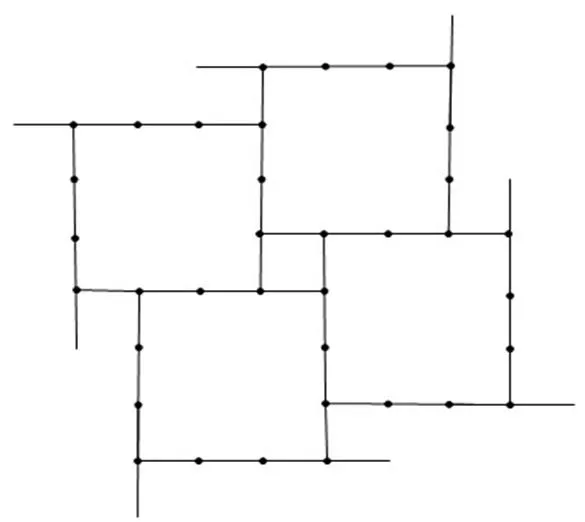
图29 平面镶嵌模型

3.2 弦 图

2002年在北京召开的国际数学家大会的会标是中国古代数学家赵爽的弦图，“赵爽弦图”通过对图形的切割、拼接，简洁巧妙地利用面积关系证明了勾股定理．在白族民居格子门窗（如图28）的图案中，如果把小正方形外围的4个四边形的对角线连接，那就形成了“赵爽弦图”．为此可以依托这一白族文化为背景，编写勾股定理的教学案例，成为当地学生了解数学史，品味数学美，探寻数学源的重要题材．

4 民俗风情中的数学元素

在大理这片富饶的土地上，勤劳勇敢的白族人民以他们多姿多彩的风土人情吸引着无数远方的客人，许多民俗文化涉及到数字、几何图案、数学运算、逻辑推理、思想方法等数学元素．在白族生活习俗中，有许多与数字有关的事情，如对3、4、8等数字的崇拜．

（1）对数字3的崇拜：古代很多学者都赋予“三”重要的意义，《说文》中提到：“天地人之道也，从数三．”《老子》中记载：“一生二，二生三，三生万物．”数字3的美好寓意也映射在白族人民的生活习俗中，如白族民间盛会“绕三灵”，即第一天绕佛都崇圣寺，第二天绕神都圣源寺，第三天绕仙都金奎寺．白族“三道茶”是白族人民招待嘉宾的一种饮茶方式，第一道是苦茶，第二道是甜茶，第三道是回味茶，即一苦二甜三回味，它告诫人们，凡事要多回味，切记先苦后甜的生活哲理．生活在剑川的白族人民在日常生活中有以下习俗，姑娘出嫁时要在嫁妆箱底放3块石头；婴儿第一次抱出门，要挂上3颗小石头．

（2）对数字4的崇拜：白族婚俗中讲究先上茶点后摆四四如意，即4碟、4盘、4盆、4碗宴席；四叶草是幸运的象征，代表着名誉、财富、爱情及健康，故在白族的扎染、建筑装饰中有许多的四叶草图案．

（3）对数字8的崇拜：背婚是白族地区普遍流行的一种婚俗，每逢十字路口，三岔道或人员集结的地方陪宾们便停下来，把嫁妆码成两大摞，让新郎背着新娘围着嫁妆绕“8”字；8大碗是白族在婚丧嫁娶或重大节庆活动时待客的盛宴，宴桌是八仙桌，一般8个人为一桌，菜肴上8个，俗称“土八碗”，大理白族传统的土八碗主要有红肉、酥肉、干香、煮白云豆、煮竹笋和木耳豆腐汤几样，一直以来，土八碗都因时因地因人而发生着变化，但8这个数字一直传承下来，亘古不变．

5 白族语言中的数学元素

语言既是文化的载体又是文化的组成部分[8]．白族是一个有语言没有文字的民族，白族历史上曾有用汉字增损或音读汉字的“古白文”，但因缺乏系统和规范，加之受时代的限制，未能延续推行．尽管白语缺乏系统和规范，但仍然成为白族地区的通用语言，目前在一些边远白族地区的幼儿园、学前班都在使用双语教学，也一贯出现白语特色的教学模式，在白语中的基数词和序数词拥有自己的发音．

基数词与白语发音表具体见表1．

表1 基数词与白语发音表

“一”分at、yi等两个不同音节，当“一”与“百”、“千”、“万”结合时，“一”读作at，而不读yi，如：at bai [一百]、at qinl [一千]；当“十”、“百”、“千”、“万”与“一”结合时，“一”读作yi而不读at，如：at bai yi [一百一]、at qinl yi [一千一（百）]．

“二”除gonx外，又读作nei、sit两个不同的音节，当“二”与“百”结合或“十”、“百”、“千”、“万”与“二”结合时，读作nei，不能读作gonx或sit，如：zaip nei [十二]、at bai nei [一百二（十）]、at qinl nei [一千二（百）]，当“二”和量词结合时，读作gonx．

数量词和名词一起组成的词组，数量词的位置都在被修饰的名词之后，如“五本书”为svi ngvx cuai（书五本）；当数词是“一”时，常省略，如“一斤盐”为binl ji（盐斤）．

量词：一对、一双，用Svnl表示；双的四分之一称为角[ko]，大理文物中元代的《段信苴宝碑》中记载“菜地三角”，即四分之三双；角的二分之一称己[tci]；己的二分之一为乏[fa]，己和乏在白语中表示耕地面积的量词[7]．

6 以白族数学文化中几何图案创设数学情境的教学案例研究

数学作为一种文化根植于各种文明之中，体现在民族建筑装饰、民族服饰、手工艺品、民俗风情等各个方面．白族文化中蕴含着丰富的数学元素，有效地将这些民族数学资源融入到当地高校、中小学的数学教学课堂，能提高民族地区的数学教育质量[9]．

案例一：白族木雕图案中的镶嵌与弦图

图28是白族民居格子门窗图案，这与初中平面几何的什么知识点有关，由此您想到什么？

（1）每一个小正方形的外围有着4个大正方形，他们构成了一个什么平面图形？

（2）如果把小正方形外围的4个四边形其中的一条对角线连接，他们构成了一个有名的图形叫什么？如何用该图证明勾股定理？

（3）如图30，如果大正方形的面积为13，小正方形的面积为1，设直角三角形的两直角边分别为、（），则等于多少？

还可提出一些与面积有关的问题……

点评：（1）从白族学生熟悉的木雕图案出发，与义务教育课程标准教科书数学中的平面镶嵌和勾股定理的知识点有机结合在一起，提高了少数民族学生学习数学的兴趣．

（2）数学源于生活，又应用于生活，该案例让学生了解赵爽利用“弦图”证明勾股定理的证法之优美、精巧．充分体现了中国古代的数学文明和数学文化．

案例二：白族扎染图案中的几何曲线

图31是白族扎染图案，其蕴含丰富的几何曲线，结合定积分的学习，你发现了什么？

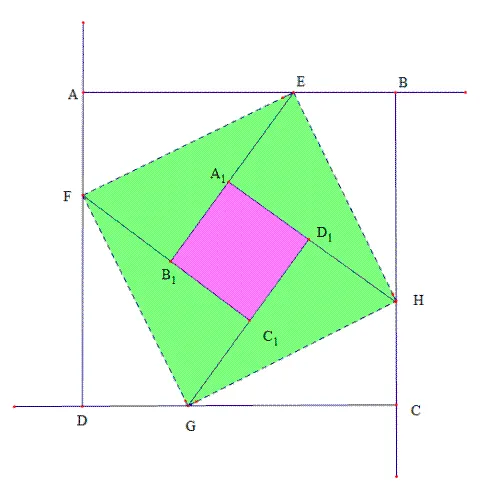
图30 弦图

图31 白族扎染图案

（1）白族扎染图案图31中蕴含有那些平面几何曲线？它们的方程分别是什么？

（3）如果把星形线绕轴旋转一周所得旋转体的体积如何计算？

（4）玫瑰线与四叶草曲线的方程之间有怎样关系？如何求四叶草曲线所围成的平面图形面积？

（5）如何计算扎染图案中一个圆形的面积？

点评：（1）具有一定解析几何和定积分知识的大学生，提出和解答以上问题并不难．

（2）借助白族扎染开展数学教学案例的研究，使在校大学生受到白族文化的熏陶，培养开发民族地区数学课程资源的意识和精神．

在大学数学的课堂教学中，用定积分探讨了圆、椭圆、玫瑰线、心形线、星形线、螺旋线等平面几何曲线的弧长以及所围成平面图形的面积，但很少涉及这些几何曲线的生活背景，如果以白族扎染图案为情境，用情境教学法在大学数学的课堂引入相关曲线概念及方程，将使大学数学更贴近白族地区生活背景，对于学生理解数学知识、激发学生学习数学的兴趣具有一定实际意义．

7 结束语

中国是个多民族国家，各个少数民族间存在着历史、语言、宗教信仰、风俗习惯等方面的差异，文化背景的差异决定了民族数学教育发展中有自身文化的特点，为在国内开展民俗数学研究提供了丰富的资源[10~13]．借助白族为研究个案，深入白族聚集区域访问调查，以白族的宗教文化、民族服饰、民俗风情、建筑装饰、白族语言等作为白族文化的研究载体，粗略挖掘了白族文化中形成和运用的数学智慧，并发现了白族文化中蕴含着丰富的数学元素．通过两个具体的教学案例研究，希望以后能为白族地区的数学课堂提供更多数学教学素材，并引入到白族地区的数学教学课堂中，这将有利于提高民族地区的数学教学质量，促进多元文化的健康发展和各民族数学文化的交流融合．

[1] 代钦．蒙古族传统生活中的数学文化[J]．内蒙古师范大学学报（哲学社会科学版），1996，（2）：42-47．

[2] 周开瑞，王世芳．羌族数学探源[J]．西南民族学院学报，2000，（4）：427-433．

[3] 罗永超．侗族数学文化面面观[J]．数学教育学报，2013，22（3）：67-72．

[4] 肖绍菊．苗族服饰的数学因素挖掘及其数学美[J]．贵州民族研究，2008，（6）：106-112．

[5] 朱黎生．彝族服饰图案中数学元素的挖掘及其在教学设计中的应用尝试[J]．民族教育研究，2012，（3）：98-102．

[6] 董建中．白族本主崇拜[M]．北京：中国国际广播出版社，2011．

[7] 大理白族自治州白族文化研究所．白族文化研究[M]．昆明：民族出版社，2010．

[8] 周长军，申玉红，杨启祥．云南德宏傣族文化中的数学因素调查分析[J]．数学教育学报，2010，19（3）：56-59．

[9] 申玉红．云南景颇民族服饰中的数学文化及其在教学中应用的探究[J]．数学教育学报，2013，22（5）：18-20．

[10] 罗永超，吕传汉．民族数学文化引入高校数学课堂的实践与探索——以苗族侗族数学文化为例[J]．数学教育学报，2014，23（1）：70-74．

[11] 杨新荣，宋乃庆．国际民俗数学研究：特点、趋势及启示[J]．民族教育研究，2011，（6）：32-35．

[12] 王培，王彭德．民间剪纸艺术中的数学文化[J]．大理大学学报，2016，（6）：13-18．

[13] 吕传汉，张洪林．民族文化与数学教育[J]．数学教育学报，1992，1（1）：101-104．

[责任编校：周学智]

Research on Mathematics in the Culture of Bai Ethnicity

YANG Meng-jie, WANG Peng-de, YANG Ze-heng

(School of Mathematics and Computer Science, Dali University, Yunnan Dali 671003, China)

In this paper, it was revealed that rich contents of mathematics were contained in the important cultural carriers of Bai ethnicity such as religious culture, ethnic costume and decoration, folk custom, building decoration, and language of Bai ethnicity. Furthermore, the commonality between the two cultures of Bai ethnicity and mathematics was discussed. It might helpful for cultural inheritance of Bai ethnicity, understanding the connotation of mathematics in the culture of Bai ethnicity, and sound development of multiculturalism.

religious culture; ethnic costume and decoration; folk custom; language of Bai ethnicity; mathematics

G750

A

1004–9894（2017）02–0080–06

2016–12–15

国家自然科学地区基金项目——地震波传播的高阶NAD算法及波场模拟研究（41464004）；云南省教育厅教学改革项目——数学与应用数学专业学生实践能力培养体系建设的实践与研究；大理大学教学改革项目——大理白族数学文化的挖掘及其高校数学课堂教学的实践（JGV-77）

杨梦洁（1993—），女，白族，云南大理人，主要从事中学数学教学与民族数学研究．王彭德为本文通讯作者．