串并联结构工业机器人D-H参数建立及算例

林少丹，傅高升，李俊达，洪朝群

(1.福建船政交通职业学院 信息工程系，福建 福州350007；2.福州大学 机械工程及自动化学院，福建 福州350116；3.厦门理工学院 计算机与信息工程学院，福建 厦门 361024)

串并联结构工业机器人D-H参数建立及算例

林少丹1，傅高升2，李俊达2，洪朝群3

(1.福建船政交通职业学院 信息工程系，福建 福州350007；2.福州大学 机械工程及自动化学院，福建 福州350116；3.厦门理工学院 计算机与信息工程学院，福建 厦门 361024)

D-H坐标系相对于6R串联型的工业机器人相对成熟，而对于2、3轴串-并联结构型的工业机器人研究较少。本文通过对传统的串联6R机器人和这类机器人进行运动分析，并根据两者之间的差别，将2、3轴串-并联结构机器人改成全串联型的D-H轴机器人，再对这种机器人采用6+1轴D-H坐标系进行了正运动学求解，最后通过ABB robotstudio对比验证6+1轴D-H坐标系，证明其是正确的。

串－并联工业机器人；D－H坐标系；运动学；离线编程

目前工业机器人完成加工作业主要采用在线示教。相对于离线编程，在线示教存在较多的缺点。采用离线编程技术，机器人运动学算法是不可或缺的，机器人运动学描述及在此基础上的运动学算法的研究是工业机器人运动关节角信息的前提[1-2]，工业机器人运动学算法的实现与机器人本身的机械结构紧密联系，即运动学算法的复杂程度取决于工业机器人本体结构。1955年Denavit和Hartenberg提出了一种机器人的建模方法[3]，其基本思想是将机器人看成是由一系列关节连接起来的连杆[4]，用连杆坐标系（又称D-H坐标系）方便的描述相邻连杆之间的关系，而用齐次变换矩阵来描述这些坐标系之间的相对位置和方向[5-6]。

近年来国内外许多学者对传统6R串联机器人(图1)的运动学作出了很大的研究贡献。而对于2、3轴串-并联结构即在关节2和关节3处采用平行四边形的6自由度机器人（图2）的运动学研究不多。本文提出6+1轴D-H坐标系法对这类机器人进行正运动学分析，在6+1轴D-H坐标系法的基础上，建立出的正运动学方程；根据机器人在不同的状态下的机器人末端位置进行运动学求解，将得到的解与ABB Robotstudio仿真软件进行对比验证。

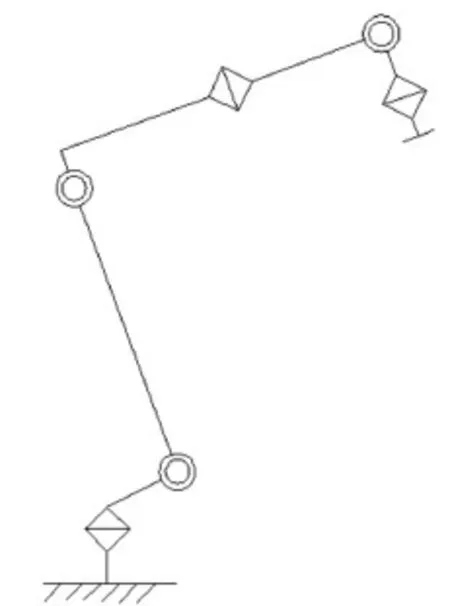
图1 6R工业机器人简图

图2 串-并联结构工业机器人简图

1 机器人运动分析及机构改型

传统6R串联工业机器人是电机通过减速器直接驱动各个轴转动的，各个轴单独运动不存在耦合现象。而这种2、3轴串-并联结构的6自由度工业机器人的第3轴的转动是通过伺服电机经过减速器驱动小臂，小臂通过平行四边形带动上臂（第3轴）运动，由于串-并联结构的工业机器人第2轴和第3轴之间存在一个平行四边形的四杆机构，且运动过程中这个平行四边形结构的机架是可变的，故机器人运动过程中2、3轴存在耦合现象。其2、3轴各自单独运动情况如下：

（1）当第2轴运动时，由于第3轴驱动电机的制动作用，小臂固定即为平行四边形结构的机架，电机驱动第2轴转动，由于平行四边形结构的关系，第3轴会做平移运动；

（2）当第3轴运动时，同样第2轴驱动电机的制动作用使第2轴固定，大臂即为平行四边形结构的机架，第3轴的驱动电机驱动小臂，小臂经平行四边形传动机构使第3轴做旋转运动。

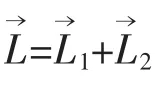
由于机器人第3轴的电机安装的位置不同，则其两种机器人的第3轴关节角的表示位置也是不同的。传统的6R工业机器人2、3轴的方位角与关节角的关系如下：

而2、3轴串并联结构的6R工业机器人2、3轴的方位角与关节角的关系如下：

图3 6R工业机器人2、3轴机构简图

一般的D-H参数是适合一系列连杆和关节组成的全串联型工业机器人，而某关节存在复合运动的混联型工业机器人如第2、3轴串-并联结构6自由度的机器人就不适合于一般的D-H参数。

由式（2）（4）可知，两种工业机器人的第3轴方位角θ2存在着一个第2轴关节角的差异。根据这个差异，将2、3轴之间的平行四边形看做一个虚关节，即将第3轴关节分解成1+1关节。如图4所示，第3’关节角的值是第2轴关节角的是负数，而第3轴关节角的值仍然是原来的数值。其运动过程：将第2轴通过平行四边形结构导致第3轴的平移，看成第2轴旋转之后再通过虚关节3’旋转合成第2轴转动的同时第3轴做平移运动。因此，就出现了6+1轴形式的机器人，将串-并联结构的工业机器人看成6+1轴的传统工业机器人。

图4 改型的2、3轴串并联结构机器人简图

2 D-H参数及转换矩阵的建立

2.1 串-并联结构工业机器人D-H参数建立

连杆坐标系（又称D-H坐标系）需要4个参数来表示，如图5为相邻连杆变换矩阵参数，其参数定义如下：连杆扭转角αi是两关节轴线i与i+1的夹角；连杆长度ai是两关节轴线i与i+1的公垂线距离；关节转角θi是相邻两条公垂线αi-1与αi的夹角；连杆偏移量di是相邻两条公垂线αi-1与αi的距离[7-8]。

在各关节上建立坐标系，让关节i的坐标系的位置和姿态转换到关节i-1上，机器人末端执行刚体的位姿变换[9-10]。其运动变换过程为：

（1）绕Zi轴旋转θi+1，使Xi轴和Xi+1轴互相平行；

(2）沿Zi轴平移di+1距离，让Xi和Xi+1平行；

(3）沿Xi轴平移ai+1距离，让连杆i+1的坐标系原点与连杆坐标系重合；

(4）使Zi轴旋转αi+1，从而让Zn轴与Zn+1对齐。

根据D-H坐标法，对改型后的2、3轴串并联结构工业机器人的结构建立D-H坐标法，如图6所示。

图5 连杆坐标系参数

图6 改进后的串-并联结构6轴机器人连杆坐标系

现以ABB IR4400工业机器人为例，根据图6连杆系坐标系建立D-H参数如表1。

表1 6+1轴D-H参数

2.2 正运动学变换矩阵

根据D-H建立运动学方程，用齐次变换矩阵i-1iT来表示连杆i坐标系在连杆i+1坐标系中的位置和姿态[11]，根据D-H法建立坐标系的原则可得：

其中Cθi表示cosθi，Sθi表示sinθi，Sαi表示sinαi,Cαi表示cosαi。

转换矩阵中的θ表示关节转角而非关节角，由于机器人运动学逆解表示的是关节角，所以要使用关节角表示转换矩阵[12]。这需要弄清关节转角与关节角之间的关系，即需要了解机器人初始位置的关节角与初始状态的关节转角。

现通过matlab robotics toolbox建立的机器人模型，其程序如下：

通过matlab robotics toolbox建立机器人模型如图7所示，并比较其初始状态位置与实际初始状态位置（如图8所示）。比较发现，使用一般D-H参数建立初始状态的机器人，其第二轴与水平成平行，而实际初始状态的机器人第2轴与水平垂直，所以要给建立的第2轴初始态添加个（-90）度。

图7 matlab中初始状态机器人模型

图8 实际机器人初始状态

故将第2轴转换矩阵写成：

其他轴的转换矩阵如下：

3 参数验证

将上式矩阵右乘，便是用6+1轴D-H模型参数建立的机器人末端坐标系的矩阵：

但是当前建立的机器人末端并非是实际机器人的末端，其与实际差了一个第6轴的轴距，因此通过转换矩阵Tp进行转换[13-14]。从基座坐标系到机器人法兰盘末端的变换矩阵为：

其中转换阵Tp:

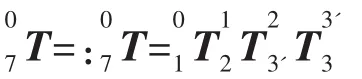
在Robotstudio里手动设置各关节角的值如图9所示。将Robotstudio得出的值与根据正运动学式（14）计算的结果进行比较，流程见图10，正运动学解见图11，其比较的值如表2。

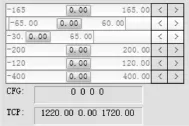
图9 Robotstudio手动设置关节角

图10 正运动学程序流程图

图11 正运动学解

表2 ABB IR4400工业机器人正运动学实验验证数据

通过表2可以发现，使用改型后的机器人计算D-H参数以及根据其建立的变换矩阵计算的TCP坐标值与实际的TCP坐标值几乎一致，表明使用这种改进后的6+1轴D-H参数模型适用于2、3轴串-并联结构的工业机器人，同时也验证了建立的正运动学的变换矩阵是正确的。

4 结束语

本研究对如2、3轴并联6自由度的机器人进行了运动分析，讨论了其运动学问题。通过对机器人计算模型的改型，建立了D-H模型参数；同时利用matlab绘制机器人初始状态与实际比较，分析出转换矩阵与关节角之间的关系。最后比较正运动学计算结果和实际机器人关节角的设置后的TCP位置验证建立的D-H参数的正确性。为研究这种串-并联结构的工业机器人的运动学打下了基础。

［1］周孝成，孟正大．KUKA机器人运动学算法的研究［J］．工业控制计算机，2014，27（9）：95－100．

［2］PRIMROSE E J F．On the input－output equation of the general 7R mechanism［J］．Mechanism and Machine Theory，1986，21（6）：509－510．

［3］KOHLI D，OSVATIC M．Inverse kinematics of general 6R and 5R，P serial manipulators［J］．ASME Journal of Mechanical Design，1993，115（4）：922－931．

［4］MANOCHA D，CANNY J F．Efficient inverse kinematics for general 6R manipulators［J］．IEEE Transactions on Robotics and Automation，1994，5（10）：648－657．

［5］于艳秋，廖启征．基于有理数运算的一般6R 机器人位置逆解算法［J］．机械工程学报，2005，41（3）：229－233．

［6］丁时锋，李清香，黄强，等．基于MATLAB的6R关节型机器人运动学仿真研究［J］．机电技术，2015（4）：52－54．

［7］DENAVIT J，HARTENBERG R S．Mechanisms based on matrices［J］．ASME Journal of Applied Mechanics，1955（6）：215－221．

［8］雷晓敏．基于CAD／CAM的工业机器人切削加工离线编程技术研究［D］．兰州：兰州理工大学，2012：9－10．

［9］高文斌，王洪光，姜勇，等．基于距离误差的机器人运动学参数标定方法［J］．机器人，2013，35（5）：600－606．

［10］王东署，迟健男．机器人运动学标定综述［J］．计算机应用研究，2007，24（9）：8－11．

［11］邓启文，韦庆，杨乐平．机械臂绝对定位精度测量［J］．计算机测量与控制，2007，15（3）：305－307．

［12］DASARI A，REDDY N S．Forward and inverse kinematics of a robotic frog［J］．Intelligent Human Computer Interaction（IHCI），2012：1－5．

［13］CHEN G S，TONG R H，QIANG B G．Analysis on flexibilityof industrial welding robots and simulation research［C］//2011 2nd International Conference on Mechanic Automation and Control Engineering，2011：81－84．

［14］王其军，杜建军．MOTOMAN机器人逆运动学新分析［J］．哈尔滨工业大学学报，2010，42（3）：451－454．

［15］陈礼聪，柯建宏.代朝旭．关节型机器人运动仿真平台的研究［J］．组合机床与自动化加工技术，2014（2）：69－71．

(责任编辑：朱联九）

The Serial-parallel Industrial Robot of the Establishment of Parameter of D-H and Example

LIN Shao-dan1,FU Gao-sheng2,LI Jun-da2,HONG Chao-qun3
(1.Department of Information Engineering,Fujian Chuanzheng Communications College,Fuzhou 350007,China；2.School of Mechanical Engineering and Automation,Fuzhou University,Fuzhou 350116,China；3.College of Computer and Information Engineering,Xiamen University of Technology,Xiamen 361024,China)

D-H method for a series type of 6R industrial robots has been developed,but the kinematics of 2,3 axis series-parallel industrial robot has not been deeply researched.The conventional series 6R robot and the robotics motion are analyzed in this paper.Based on the difference between the two robotics motion,the 2,3 axis series-parallel industrial robot is turned into a series type of 6+1 axis robots.In this way,inverse kinematics problems are solved using 6+1 Axis D-H method.Finally,the 6+1 axis D-H method is verified by ABB robotstudio contradistinction,which proves it is correct.

series-parallel industrial robot;D-H method;kinematics;off-line programming

TP242.2

A

1673-4343（2017）02-0035-07

10．14098／j．cn35－1288／z．2017．02．007

2016-12-19

林少丹，男，福建闽侯人，副教授。主要研究方向：嵌入式系统，工业机器人。