类神经传导的布朗直线模型

梁明杰，郑巧玲，潘荣彬，旦巴多吉，许佳淮

(三明学院 信息工程学院，福建 三明365004)

类神经传导的布朗直线模型

梁明杰，郑巧玲，潘荣彬，旦巴多吉，许佳淮

(三明学院 信息工程学院，福建 三明365004)

基于神经传导原理构造了一类称为布朗直线的随机直线模型。借助布朗运动的相关性质该模型有效地刻画了神经传导路径的多重性与不确定性。进一步地，讨论了该模型的几何特征并给出了相应的概率估计。

神经传导；布朗直线模型；几何特征；概率估计

布朗运动最早是由英国生物学家Brown在1827年提出的。Wiener、Einstein、Levy等人进一步对布朗运动的轨道性质的研究[1]。随着布朗运动的逐步发展，又可应用到数学分析和概率论的领域中，逐渐成为不可或缺的重要理论基础。对布朗运动的研究至今仍在继续，研究成果十分丰富[2-5]。

神经末梢分布在各种器官和组织中，影响着人们的感观和运动,这些感观和运动都是靠神经传导的。该传导过程是电化学的过程，是在神经纤维上顺序发生的电化学变化[6]。在细胞膜上任何一点产生的动作电位会不衰减地传播到整个细胞膜上，这称之为动作电位的传导。如果是发生在神经纤维上，传导的动作电位又称为神经冲动。以神经元为例，动作电位沿轴突的传导是通过跨膜的局部电流实动作电位在神经纤维上的传导实现的。学者们在研究中发现，神经系统神经元的分布都具有明显的分形特征。事实上，布朗运动的样本轨道是由大量无规则可循的折线组成，是一种处处连续但处处不可微的曲线，是一种具有自相似分形特性的无规则曲线。本文根据神经传导原理构造了一类布朗直线模型。针对于布朗直线模型，我们借助布朗运动的相关性质有效地刻画了神经传导路径的多重性与不确定性，进一步地，讨论了该模型的几何特征并给出了相应的概率估计。

1 布朗直线的构造

人体的神经传导系统是一个及其复杂的流路分支系统[7]，其结构与复杂网络有许多相似之处，著名的神经网络算法就是基于神经传导系统的相关原理而构建的。神经传导的路径载体神经纤维具有繁杂的神经末梢分支，对于神经传导系统而言，当人体接受外界刺激时，要把刺激信息传递给大脑或中枢神经系统就必须通过神经纤维作为路径载体，根据神经纤维的复杂结构，刺激信息的传导路径可看成是并串联的复杂网络电路系统[8]，由于传导过程路径的长短不一且能量会随之发生损耗，故人体感应外界刺激有快慢之分，也有强弱之分[9]。基于上述有关神经传导的复杂原理，因此建立了如图1的布朗直线模型，该模型较直观的描述了神经传导快慢强弱的特性，且有效地刻画了神经传导路径的多重性与不确定性。

图 1布朗直线模型

如图1所示，称由A(B1(t),a)，B(B2(t),b)两点所确定的随机直线为布朗直线，其中B1(t)与B2(t)为相互独立的一维标准布朗运动。事实上，可以将A、B看作神经的前、末端，由于两端间有很多分支，根据其传导路径的多重性和不确定性，可简化成上述布朗直线模型。

记过A、B两点的布朗直线为lAB(t)，则其方程过程描述如下：

当B1(t)≠B2(t)时，

当B1(t)=B2(t)时，

显然对于任意t＞0，有

从而只考虑B1(t)≠B2(t)的平凡情形。设d（t）为坐标原点（0,0）在t时刻到布朗直线的距离lAB(t)，即有

2 布朗直线的几何特征及其概率估计

为便于讨论，先给出一个重要引理。

下面的命题给出了布朗直线夹在A与B两点间直线段的随机长度在某一时刻的概率分布。

命题1 对任意t＞0，a＞b，有

当L＞a-b时，有

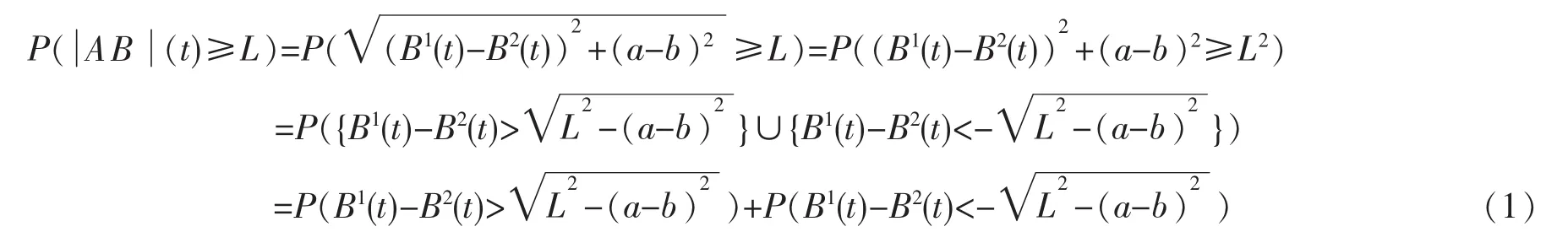
由于B1(t)与B2(t)相互独立且Bi(t)～N（0，t），i=1,2，故有B1(t)-B2(t)～N（0，2t），从而有

综上（1）～（3）式，有

下面的命题给出了布朗直线夹在A与B两点间直线段的随机长度在某一时间段的概率估计。

命题2 对任意L＞a-b＞0，t＞0，有

证明 一方面，有

根据引理1（2），有

和

又根据引理1（1），有

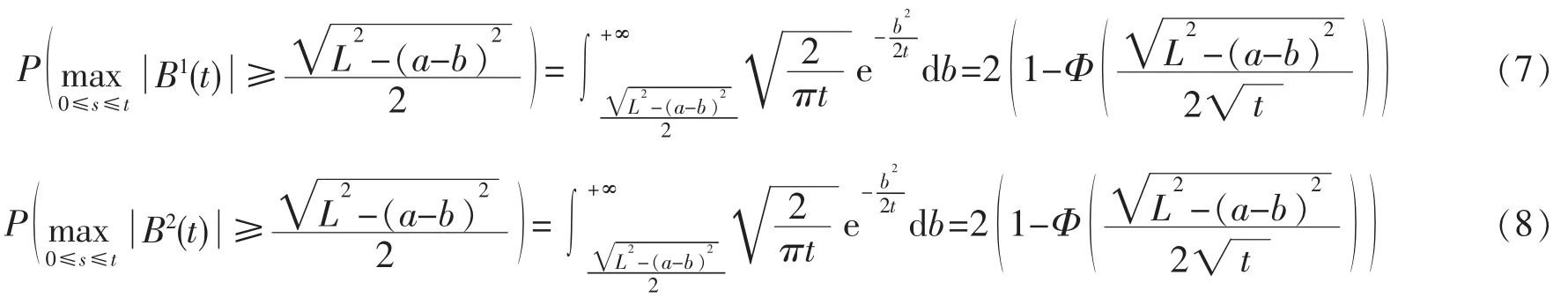
综上（4）～（8）式，有

另一方面，根据命题1有

命题3 对任意l＞0，t＞0，有

证明 根据d（t）的定义，有

利用B1(t)与B2(t)的独立性，有bB1(t)-aB2(t)～N（0，（a2+b2）t）从而有

综上（9），（10）式命题得证。

命题4 对任意l＞0，t＞0，有

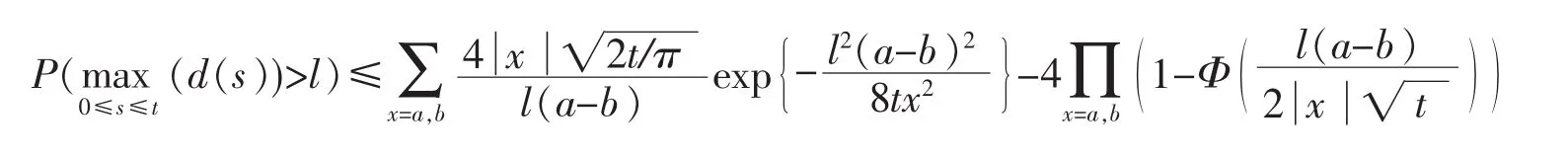
证明 根据的定义，有

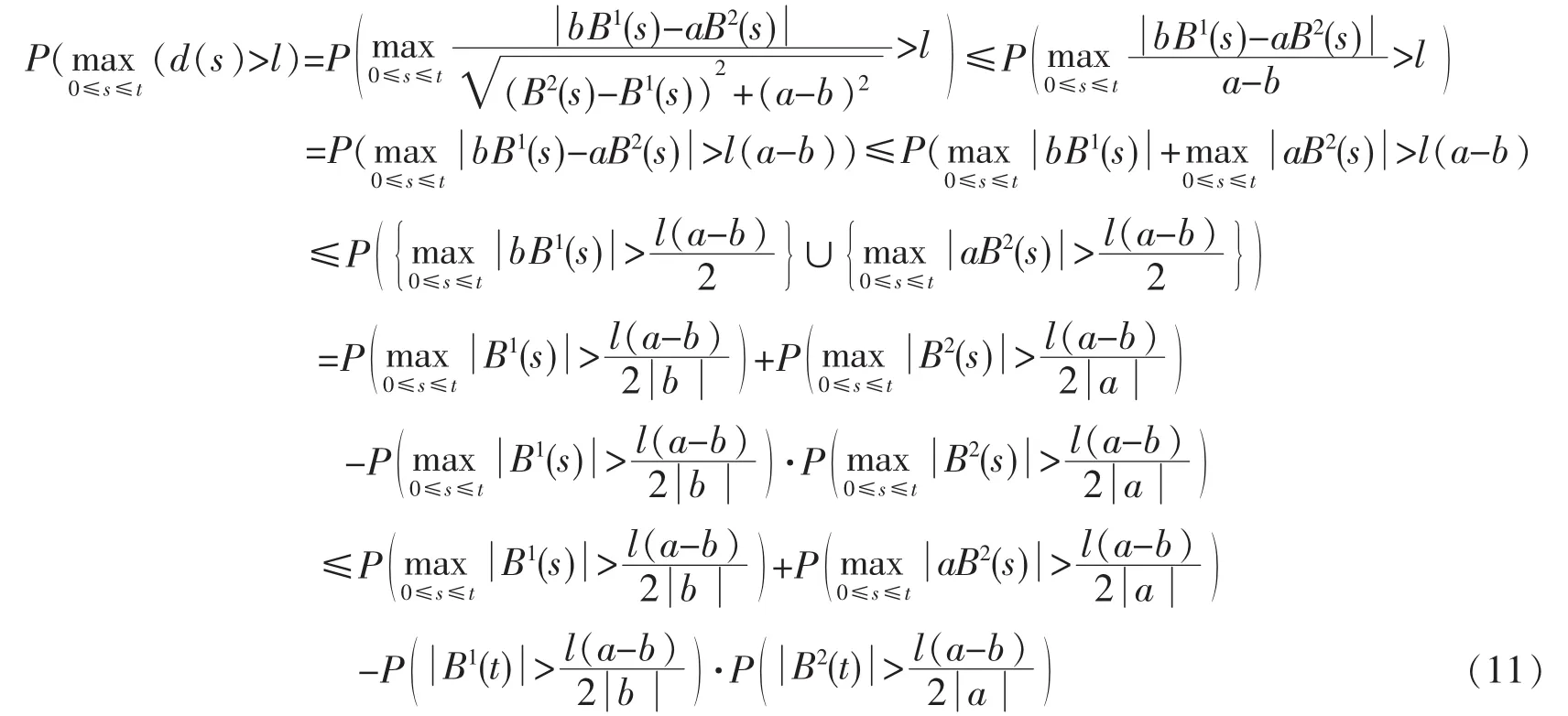
根据引理1（2），有

又根据引理1（1），有

综上（11）～（15）式命题得证。

3 结束语

虽然本文所构造的布朗直线模型能较合理的描述与刻画神经传导的相关特征，但该模型的建立是在一定的优化假设基础上的，要真实地完全刻画现实中复杂的神经传导问题还有待对模型作进一步修正与改进。

［1］钱敏平，龚光鲁．随机过程论［M］．北京：北京大学出版社，2000．

［2］王梓坤．布朗运动首中与末离的联合分布［J］．科学通报，1994，39（13）：1168－1173．

［3］郝柏林．布朗运动理论一百年［J］．物理，2011，40（1）：1－7．

［4］孙荣恒．随机过程及其应用［M］．北京：清华大学出版社，2003．

［5］KARATZAS I，SHREVE S．Brownain motion and stochastic calculus［M］．Berlin：Spriger Verlag World Publishing Crop，1988．

［6］袁运开，顾明远．科学技术社会词典：生物［M］．杭州：浙江教育出版社，1992．

［7］元小冬．轻松学习肌电图：神经传导功能与肌电图检查指南［M］．北京：北京大学医学出版社，2007．

［8］张荣华．神经信息传导的电路模型［D］．天津：天津大学，2010．

［9］赵曙光，秦明新．神经传导速度检测仪的研制［J］．数据采集与处理，1998（a10）：91－94.

（责任编辑：朱联九）

Brownian Line Model as the Similar Nerve Conductive

LIANG Ming-jie,ZHENG Qiao-ling,PAN Rong-bin,DAN Ba-duoji,XU Jia-huai
(School of Information Engineering,Sanming University,Sanming 365004,China)

Based on the principle of nerve conduction,a class of the random line model which is defined Brownian line is constructed in this paper.Through the relative properties of Brownian motion,the multiplicity and uncertainty of the nerve conduction pathways are effectively described by this model.Furthermore,the geometrical characteristics of Brownian line are discussed,and the estimations of some relative probabilities are given.

nerve conductive;Brownian line model;geometrical characteristics;probabilities estimations

O211.6

A

1673-4343（2017）02-0006-05

10．14098／j．cn35－1288／z．2017．02．002

2016-12-30

国家自然科学基金青年项目（11601083；福建省自然科学基金青年创新项目（2016J05002）；福建省中青年教师教育科研项目（JA15476）；福建省大学生创新创业训练计划项目（201511311025）

梁明杰，男，广东梅县人，讲师。主要研究方向：随机过程及其应用。