哲学思想在高等数学教学中的应用

吴 娟 梁娟英 崔 艳

（1.亳州职业技术学院 安徽 亳州 236800；2.淮北师范大学 安徽 淮北 235000）

哲学思想在高等数学教学中的应用

吴 娟1梁娟英2崔 艳1

（1.亳州职业技术学院 安徽 亳州 236800；2.淮北师范大学 安徽 淮北 235000）

高等数学中蕴含着丰富的哲学思想，比如有限与无限、量变与质变、运动与静止、现象与本质，特殊与一般以及以退为进的思想等。结合平时的教学，探讨了哲学思想在数学教学中的应用，并取得了非常好的效果。通过从哲学的角度辅助的讲解数学，不仅使学生更深刻的理解数学本质，还能培养学生的辩证思维能力，最终达到知识教育和素质教育的目的。

高等数学；哲学；教学

数学课程给人的印象似乎就是介绍公式，讲解定理以及复杂的计算，数学似乎与哲学并没有什么关联。然而实际上这种认识并不准确。数学家Bordas指出“没有数学，难以得知哲学的深度，没有哲学，当然也难以得知数学的深度，两者相互依存”。恩格斯说：“数学是辩证的辅助工具和表现形式”。可以看出数学与哲学始终存在着密切联系，比如：导数与积分，常量与变量，有限与无限，局部与整体，运动与静止，近似与精确，现象与本质等等。在数学教学中，应充分揭示数学中蕴含的哲学思想，不是从简单的数学公式介绍与数学计算的层面，而是从哲学的层面辅助讲解数学思想，不仅能使学生对于数学的本质有更深刻的理解，而且还可以提高学生的辩证思维能力，培养学生用辩证唯物主义观点分析问题，解决问题的能力。本文将结合自己平时的教学，探讨哲学思想在高等数学教学中的应用。

1.有限与无限思想在教学中的应用

初等数学与高等数学的研究对象不同，后者研究的是变量、运动，而前者相对简单，研究的是常量、静止。有了运动和变化，就可以研究行星的运行，液体的流动，动植物的生长，流行病的传染，利润的波动等。而理解运动和变化的关键，乃是找到驯服无限的方法[1]。有一个著名的关于运动的悖论，是由希腊哲学家芝诺提出的：故事说阿基里斯要在100米的历程中追乌龟，阿基里斯的速度是乌龟速度的10倍。乌龟位于阿基里斯前方10米，比赛开始，当阿基里斯跑到乌龟的起跑点时，乌龟已经向前跑了1米；当阿基里斯向前又追赶1米时，乌龟又向前领先米；阿基里斯向前追赶米时，乌龟还是领先阿基里斯米，这个过程一直无限下去，尽管两者距离越来越近，但阿基里斯永远在乌龟后面。这显然是一个悖论，而理解这个悖论，就必须找到处理无限的方法。

上述例子深刻体现出有限与无限的辩证思想，有限和无限既是对立矛盾的又是统一的整体。有限可以表示无限，无限又由有限组成，两者在一定条件下还可以相互转化。正如恩格斯所说：“无限来自于有限，永久来自于暂时”。

无限是有限的发展，那么对于“有限”成立的命题，对于“无限”还会成立吗？显然不一定，比如但是（“1∞”不一定等于1）还有不一定是0或1了，这也体现了另一个哲学思想即质量互变思想。

2.量变与质变思想在教学中的应用

极限概念就是高等数学中一个体现出从量变到质变过程的生动例子。极限就是“变量无限地向有限的目标逼近而产生量变到质变的转化”[2]。例如，“割圆术”求圆的面积的原理是：用内接正多边形的面积近似代替圆的面积。当正多边形的边数不断增加，正多边形的面积就越来越近似于圆的面积，但只要正多边形的边数有限，正多边形的面积始终是圆面积的近似值，在这里体现了量变；但当多边形的边数无限增加时，正多边形的面积就是圆的面积了，这就是质变。还有一元函数推广到多元函数的时候，自变量个数增加了，有的性质也会发生质变。在高等数学课程中，体现出从量变到质变的例子有不少，教师在教学中应当引导学生通过质量互变哲学思想，理解概念之间的区别与联系，这样就不会犯类似于1∞=1这种想当然的错误了，从而提高了学习效果。

3.局部与整体思想在教学中的应用

芝诺的另一个关于运动的悖论是“飞矢不动”。即这支箭在某一瞬间可以看作是静止的，但是如果每一瞬间这支箭都是静止的，那它又怎么可能运动呢？这个悖论在于孤立的考察某一瞬间，它是不动的，物体的运动有其前因后果，即由前后位置的比较反映出来的，有比较才会产生速度[3]。因此在引入导数的物理背景求物体的t0时刻瞬时速度时，也不能仅仅只考虑t0时刻，而是从这一时刻的附近出发，求该时刻附近的平均速度，然后让t→t0，平均速度的极限就是t0时刻的瞬时速度。通过这个运动悖论，我们体会到了导数概念的“局部”性。这就告诉我们不能孤立的、静态的考察一个点，而是用动态的思想，通过考察其附近（局部）的性质，反过来研究该点的性质。就好像我们在了解一个人时，也不能仅仅从这个人本身出发，还要看其周围的环境，比如他的家庭背景，社会关系等，这样才能更全面，更透彻的认识一个人。

微积分核心思想之一就是“局部”，比如导数，微分，极值，单调性，凹凸性，拐点等。而连接局部和整体的桥梁就是微分中值定理f(b)-f(a)=f'(ξ)(b-a)，等式左边是f的整体性质，右边是局部性质，通过研究左边的局部性质，才能更好的了解右边的整体性质。

在定积分的几何背景，即求曲边梯形面积的过程中，也充分体现了局部和整体的哲学思想。求曲边梯形的面积没有现成的公式可以用，思路是从局部出发，转化为小曲边梯形，再进行累积，得到整体曲边梯形的面积。

dx表示小曲边梯形的宽，f(x)表示小曲边梯形不断变化的高，ds=f(x)dx表示小曲边梯形的局部面积，就表示大曲边梯形的整体面积，这种通过微元（局部的观点）来理解积分，虽然不太严格，但形神兼备，简易而清晰[3]。比起常规的“分割，近似，求和，取极限”这种严格的定积分定义，学生更容易接受上述形象化的解释，更符合高职学生的认知水平。

总之，局部和整体是对立统一的，整体是由局部构成的，通过研究局部的性质，更容易理解整体的性质，这是高等数学有效的数学方法。

4.现象和本质辩证思想在教学中的应用

在数学的学习中，一定要教会学生通过现象认识本质，这样才能更深刻地了解数学的概念。比如，定积分和不定积分，虽然都是积分，但是定积分表示一个和式的极限，是一个数，而不定积分是原函数的全体。两者既有区别又有联系，牛顿和莱布尼兹通过微分中值定理把两者联系起来了，这也标志着微积分这门学科的诞生。

另外，还有导数，定积分，二重积分，三重积分，曲线积分，曲面积分，无穷级数本质上都是极限，因此都满足极限的线性性质。也说明了极限是微积分这门学科的主线，把看似零散的知识点都联系起来了。

行列式和矩阵是线性代数中两个重要概念，虽然都可以求线性方程组的解，但本质不同，行列式是一个数，而矩阵是一个数表。两者之间既有本质区别，又有一定联系。一方面矩阵的秩是通过行列式定义的，另一方面用行列式求解线性方程组和用矩阵求解线性方程组解的公式是一致的，说明行列式和矩阵在求解线性方程组方面是密切联系的。比如：设线性方程

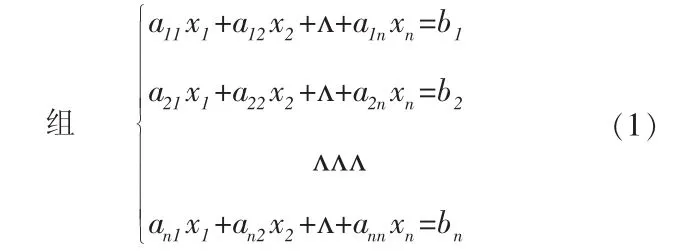
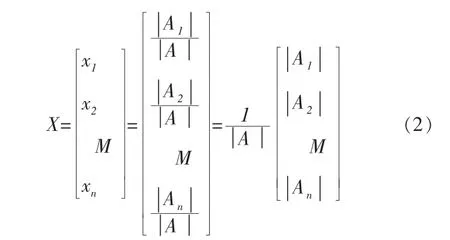
方法一：克莱姆法则。

方法二：逆矩阵法。

方程组（1）对应的矩阵方程为AX=B得出X=A-1B

上面两种方法虽然不同，但实际上利用克莱姆法则给出的求解公式（2）与利用逆矩阵法给出的求解公式（3）是统一的[4]。这是因为当

5.以退为进思想在教学中的应用

以退为进，退只是表面现象，最终的目的是为了进。比如，求曲边梯形的面积时，没有直接的公式可以用，先退一步求其面积的近似值，然后取极限，进而求得该面积的精确值。再如求y=xx的导数时，幂指函数y=xx既非幂函数也非指数函数，求导时也无公式可用。因此，退一步，等式两边先取对数，使之转化为隐函数，这样就能顺利求导了。这种以退为进的思想方法不仅可以解决数学中的问题，而且还可以培养学生的探索能力和创造性思维能力，训练反常规思维和抽象思维[5]。

总之，数学的本质是哲学。在高等数学的教学中，充分展现其蕴含的哲学思想，会起到事半功倍的效果，不仅能使学生在更高的层面掌握微积分的基本思想，方法，把握其精髓，提高教学效果，还能培养学生灵活运用辩证的思维分析问题，解决问题的能力，因而这也是一种有效提升学生在数学方面的基本素养，进而提升职业素养的实用方法。

[1］齐斯.德福林.数学的语言[M].广西师范大学出版社,2013.

[2］魏玲等.高等数学中的哲学思想及其在独立学院教学中的应用[J].大学教育, 2015（09）：133-134.

[3］张奠宙等.情真意切话数学[M].科学出版社,2011.

[4］何立国，施武杰.以线性方程组为中心展开线性代数课程的教学[J].大学数学, 2009,25(6):203-206.

[5］陈翠芳.谈数学分析教学中哲学思想的渗透[J].山西高等学校社会科学学报，2001（13）:98-99.

[6］康晓辉.高等数学中蕴涵的哲学思想[J].职业时空,2009（09）：134-135.

The application of philosophical thought in teaching and learning of advanced mathematics

Wu Juan1Liang Juan -ying2Cui Yan1
(1.Bo zhou Vocational and Technical College Anhui Bozhou 236800；2.Huaibei Normal University Anhui Huaibei 235000）

Higher Mathematics contains rich philosophy thoughts,such as the limited and the unlimited,the quantitative and qualitative change, motion and motionlessness phenomenon and essence,special and general thoughts and so on.This paper,connecting the ordinary teaching,discusses the application of philosophical thought in mathematical teaching,and achieves very good results.Through explaining maths from the philosophy angle,it not only makes the students more profoundly understand mathematical essence,but also fosters the students’ability of dialectical thinking,ultimately achieving the purpose of knowledge education and quality education.

Higher Mathematics；Philosophy；Teaching

B014

A

2095-7327（2017）-04-0106-03

职业素养视角下开展高职数学文化教育的研究与实践—亳州职业技术学院院级课题，课题编号为2015bzjyxm05。

“安徽省高等学校省级质量工程重点项目”“职业素养视角下独立学院数学文化教育的研究”，基金编号为2016jyxm0936。

吴娟（1982—），女，安徽亳州人，就职于安徽亳州职业技术学院基础教学部，讲师，硕士研究生，研究方向为分形几何、数学教育。