亏损矩阵的特征值灵敏度分析

席雅丽，刘志明，代金文

(长春工程学院理学院，长春 130012)

亏损矩阵的特征值灵敏度分析

席雅丽，刘志明，代金文

(长春工程学院理学院，长春 130012)

根据若当标准形理论，首先引入亏损矩阵的广义特征向量及其伴随向量系概念，利用它们的双正交性解耦了灵敏度控制方程，其次通过分析解耦后的控制方程的恒等性条件，提出了亏损矩阵特征值的灵敏度分析算法，发展了若当标准形理论在亏损系统的解耦及控制中的应用范围。数值算例证明本文算法的正确性及有效性。

亏损矩阵；灵敏度分析；广义特征向量；正交规范；特征值

灵敏度分析是指在结构分析中引入设计参数，把系统的性质矩阵(M、C、K)和模态参数(λi，ui)均视为该设计参数的函数，并把它们关于设计参数的偏导数称为灵敏度。可见灵敏度即为求导信息，它是一种度量，是一种评价由于设计变量或参数的改变而引起结构特性变化的程度的方法。系统灵敏度分析的主要目的是确定设计参数变更时，系统响应、特征值及特征向量等发生的变化率，因此，通过灵敏度分析可得到为实现最优化所需要的设计导数。它是当前力学和结构工程领域的主要研究方向之一，广泛地应用在结构优化、可靠性评估及结构控制等工程领域。在很多结构系统中即使出现密频或重频[1]的问题，也经常假定系统为完备系统来分析灵敏度，然而在非比例阻尼矩阵，或在非保守力作用下的结构动力问题，如气动弹性颤振分析以及结构和控制系统相耦合[2]的问题等，其状态矩阵可能是亏损的。事实上，当非经典阻尼系统的非经典模态对应的特征值的几何重数小于其代数重数时，就必定会出现亏损系统的特征问题。许多流固耦合动力学问题、自动控制问题中也经常会遇到亏损特征值问题。亏损状态矩阵的特征子空间是不完备的，因此，利用非亏损状态矩阵的特征向量的正交性[3]实现灵敏度分析的方法已不再适用，目前这方面的研究还处于发展阶段。张慧生等[4]提出了一般矩阵的亏损特征对的摄动方法，却不属于灵敏度分析方法的范畴。文献[5-6]开始引入广义特征向量理论展开对亏损线性振动系统特征向量的灵敏度研究，文献[7]从亏损系统的特征问题出发，利用广义模态理论建立亏损系统广义模态向量系进行模态灵敏度的分析，文献[8]提出了重频完备系统的所有频率灵敏度算法，但目前关于重频亏损系统特征值的灵敏度分析算法的文献还未出现。

本文依据亏损矩阵的若当标准形理论，通过广义特征向量及其伴随向量系的双正交性，推导出亏损矩阵特征值的灵敏度表达式。数值算例说明了结果的正确性。

1 亏损矩阵的广义特征向量及其伴随向量系

设振动系统所对应的状态矩阵为N阶方阵A，其一般特征问题为Aφ=λφ。由《矩阵论》可知，每个N阶复数矩阵A总能与一个若当标准形相似，若不计若当块在对角线上的顺序，A的若当标准形是唯一的。当每个若当块的阶数均为1时，A的若当标准形就是对角形，此时A必有N个线性无关的特征向量，可见对角形只是若当标准形的特殊情形。可见，复矩阵A可对角化的充分必要条件是A的特征矩阵的初等因子全为一次式。

若λ是A的一个m重特征值，其几何重数小于代数重数时，A为亏损矩阵，为了讨论方便，假定A的其余特征值均为单特征值，则A的若当标准形为

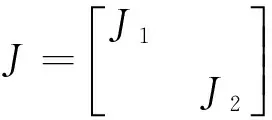
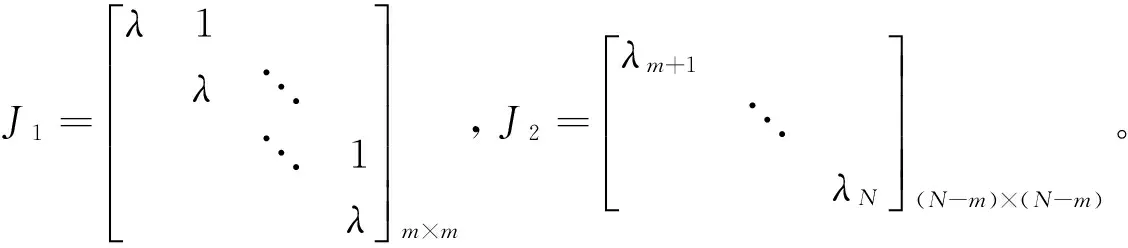
矩阵A对应的若当问题为

AY=YJ，

(1)

并可得特征方程组为

(2)

由式(2)解得y1，y2，…，yN称为A的广义特征向量，它们是线性无关的，并记Y=[y1，y2，…，yN]。引入y1，y2，…，yN的线性无关伴随向量系x1，x2，…，xN，令它们满足狄利克利规范正交化条件

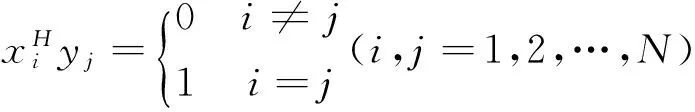
(3)

记X=[x1，x2，…，xN]，则上式可写成

XHY=E，

其中(•)H表示共轭转置。

取式(2)的部分特征方程构成下式

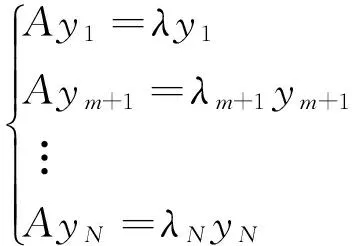
(4)

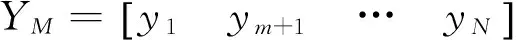
(5)

由式(4)可知

AYM=YMΛ，

(6)

其中

Λ=diag(λ，λm+1，…，λN)，

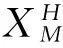
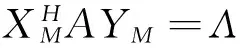
(7)

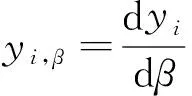
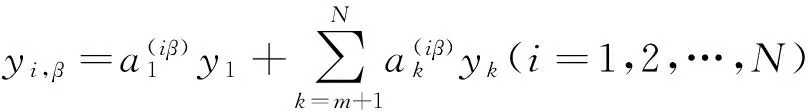
(8)

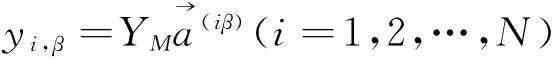
(9)

同理，将xi，β表示为线性无关组x1，xm+1， … ，xN的线性组合

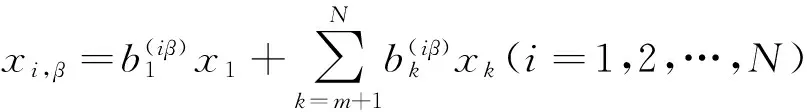
(10)

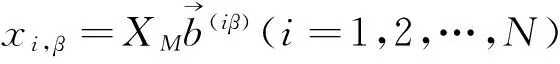
(11)

现在来讨论m重亏损特征值λ的灵敏度λ，β，对式(4)第1个方程关于设计参数β求导，得控制方程为

A，βy1+Ay1，β=λ，βy1+λy1，β，

(12)

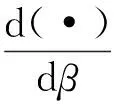
(A-λE)y1，β=(λ，βE-A，β)y1，

(13)

将式(9)代入式(13)得

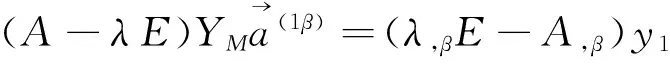
(14)

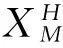
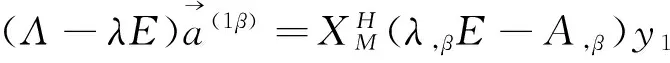
且有

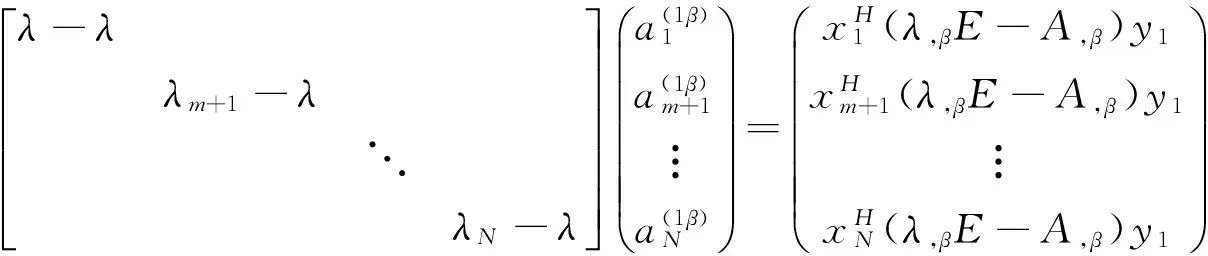
(15)

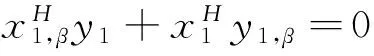
(16)

将式(9)和式(11)代入式(16)得

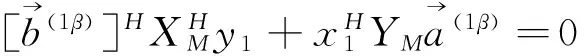
根据正交性条件式(5)有

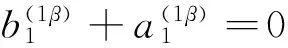
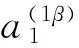
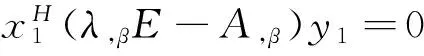
即m重亏损特征值λ的灵敏度为

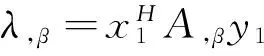
(17)

为求各单特征值λm+1，…，λN的灵敏度，对式(4)的其余方程关于设计参数β求导得控制方程为

A，βyl+Ayl，β=λl，βyl+λlyl，β(m+1≤l≤N)，

(18)

整理式(18)得

(A-λlE)yl，β=(λl，βE-A，β)yl(m+1≤l≤N)，

(19)

将式(9)代入式(19)得

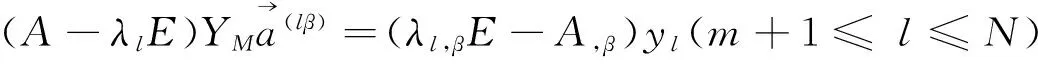
(20)

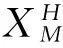
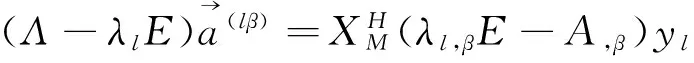
且有

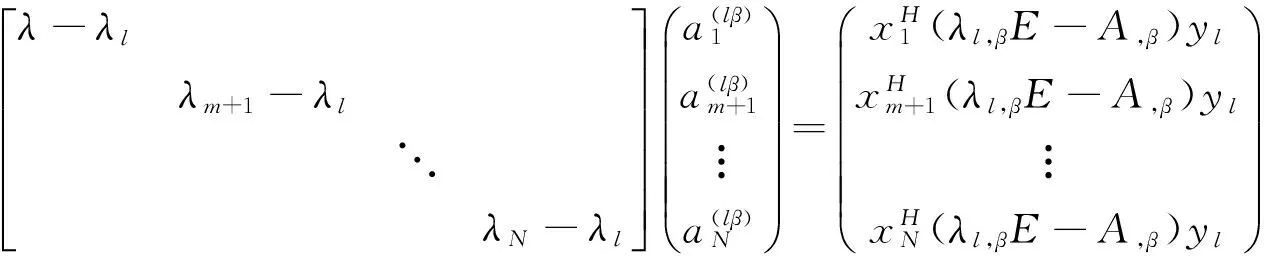
(21)

式(21)中只有第l-m+1(m+1≤l≤N)个方程为无效方程，且有

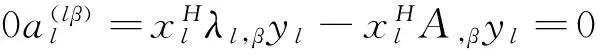
即

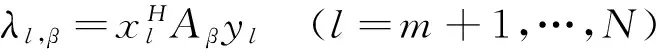
(22)

由式(17)和式(22)可知，亏损矩阵(系统)的全部特征值的灵敏度精确表达式已经获得，下面用2个数值算例来验证结论的正确性。

2 数值算例

设某线性振动亏损系统对应的状态矩阵如下：

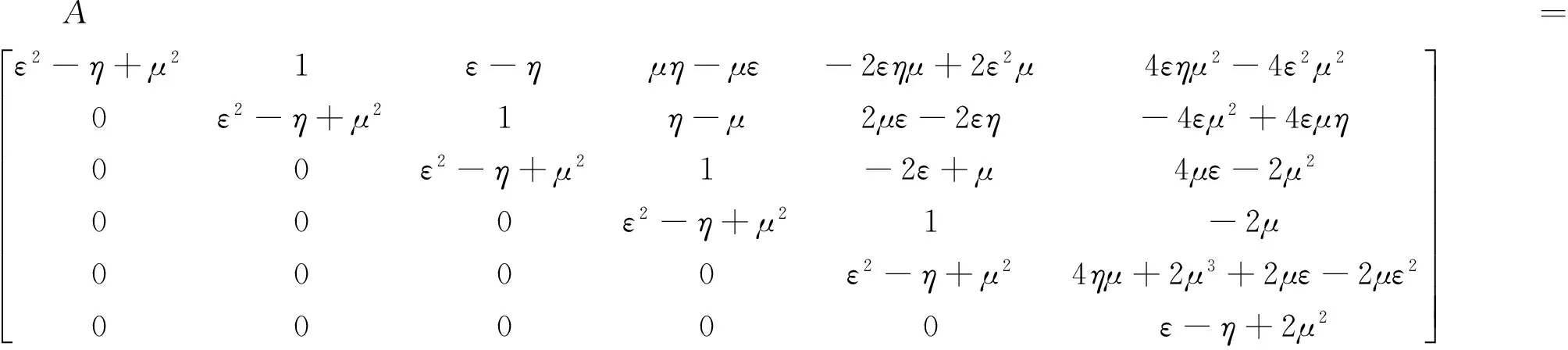
则A的Jordan型矩阵为

当ε=η=μ=2时

它有一个5重亏损特征值λ1，2，3，4，5=λ=6和1个单特征值λ6=12。其若当标准形为

根据式(2)解出广义特征向量，然后求其伴随向量，并把它们按式(3)规范化为

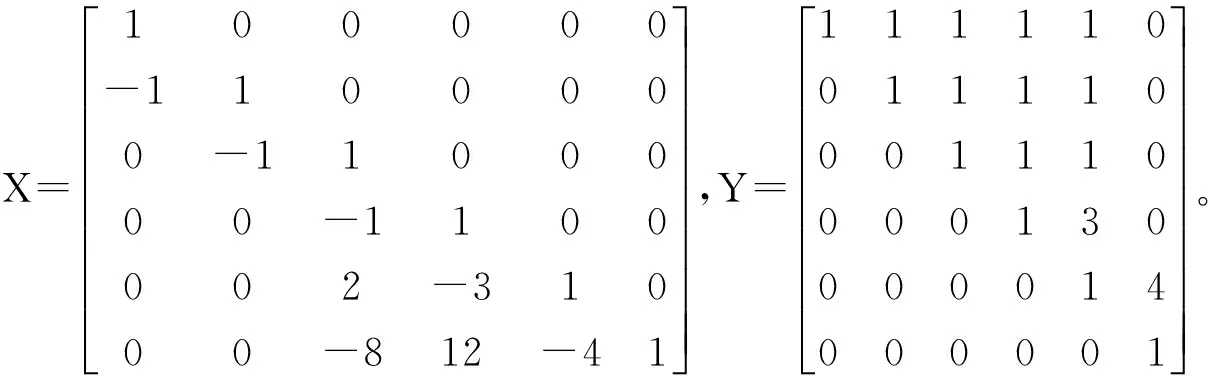
以ε为设计变量则根据式(11)与式(17)求得灵敏度分别为

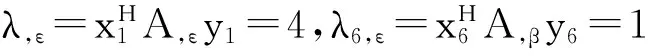
(23)

相应地，取变化率Δε=0.1时差分灵敏度为

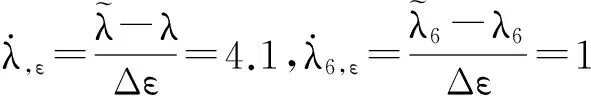
(24)

对比式(21)和式(22)，可见本文算法所得的特征值灵敏度的正确性。同时由于差分灵敏度需反复计算设计参数扰动后的状态矩阵及其特征值，并且当设计参数扰动量的取值变化较大时，差分灵敏度存在不稳定性。而本文所给出的灵敏度计算方法，只需在系统的初始状态下就可求出全部特征值的灵敏度，与设计参数的扰动量无关，并能取得良好的精度，其计算代价更小，数值上更稳定，可见本文算法更为有效。

3 结语

本文针对亏损矩阵的特征值，应用亏损矩阵的广义特征向量及其伴随向量系的正交性，实现控制方程的解耦，通过讨论无效方程的恒等性来获得亏损系统全部特征值的灵敏度表达式。数值算例说明了本文算法的正确性和有效性。

[1] 张淼，于澜，鞠伟.重频结构模态灵敏度分析的高精度截模态算法[J].振动工程学报，2014，27(4):526-532.

[2] 张淼.亏损结构振动方程的稳态响应求解[J].吉林师范大学学报：自然科学版，2014，35(1)：91-94.

[3] 张淼，于澜，鞠伟.复模态正交性理论的异常现象及对策分析[J].应用数学和力学，2014，35(10)：1081-1091.

[4] 张慧生，王文亮，张振宇.亏损特征值问题的摄动分析[J].复旦学报：自然科学版，1997，36(2):121-129.

[5] 时国勤，诸德超.线性振动亏损系统的广义模态理论[J].力学学报，1989，21(2):183-191.

[6] 时国勤，诸德超，王俊奎.线性振动亏损系统的广义模态参数的识别方法[J].固体力学学报，1991，12(3):235-241.

[7] 张淼，于澜，鞠伟.亏损振系广义状态向量灵敏度的移频算法[J].计算力学学报，2013，30(6)：872-878

[8] 张淼，于澜，鞠伟.重频系统的频率灵敏度分析算法研究[J].华南师范大学学报：自然科学版，2014，46(3)：40-44.

The Sensitivity Analysis to the Eigen Value of the Defective Matrice

XI Ya-li，et al.

(SchoolofScience，ChangchunInstituteofTechnology，Changchun130012，China)

Based on the theory of standard form，the generalized eigen vector of the loss matrix and the concept of the adjoint vectors are introduced in this article.The sensitivity control equation is decoupled by their orthogonality.Then，by analyzing the identity of the decoupled control equation，the sensitivity analysis algorithm to the eigen value of the defective matrice has been proposed，and the application range of the standard form theory in the decoupleing and controlling of the loss system are developed.The numerical examples prove the correctness and validity of this algorithm.

defective matrice；sensitivity analysis；generalized eigenvector；orthogonal specification；eigen value

10.3969/j.issn.1009-8984.2017.01.029

2017-02-12

吉林省自然科学基金项目(20160101277JC) 吉林省大学生科技创新项目(201611437051) 长春工程学院校青年基金项目(320160018)

席雅丽(1980-)，女(汉)，长春，硕士，讲师 主要研究计算数学。

O321

A

1009-8984(2017)01-0125-04