透过椭圆焦点看物理规律1)
徐康刘章军
∗(武汉理工大学土木工程与建筑学院,武汉430070)
†(三峡大学土木与建筑学院,湖北宜昌443002)
透过椭圆焦点看物理规律1)
徐康∗刘章军†,2)刘章军,通讯作者,博士,教授,博士生导师,主要从事土木工程的教学与研究.E-mail:liuzhangjun73@aliyun.com
∗(武汉理工大学土木工程与建筑学院,武汉430070)
†(三峡大学土木与建筑学院,湖北宜昌443002)
介绍了不同学科领域里与椭圆有关的3种物理规律:光线反射规律、开普勒第二定律、细杆平衡规律,并对其进行相互推导,得出结论:这3个物理规律是等价的,它们的本质都是椭圆所特有的几何特征,它们只是这一本质在不同领域的不同表现.
物理规律,椭圆,光学,天文学,静力学
椭圆是圆锥曲线中的一种,古希腊数学家阿波罗尼奥斯(Apollonius,约公元前262–公元前190年)曾系统地研究过圆锥曲线,他在前人研究的基础上,加上他自己所独创的成果,编写了经典巨著《圆锥曲线论》(Conics)[1].直到今天,在各种学科领域里与椭圆有关的研究还在继续.在研究过程中,人们发现了与椭圆有关的几种物理规律,在光学上,从椭圆一个焦点发出的光线经椭圆壁反射后,反射光线都汇聚到椭圆的另一个焦点上.如图1所示,这是光线在椭圆内壁中的反射规律,以下简称光线反射规律.

图1 光线反射规律图
在天文学上有开普勒三定律,第一定律为:所有行星绕太阳的轨道都是椭圆,太阳在椭圆的一个焦点上.第二定律为:行星和太阳的连线在相等的时间间隔内扫过相等的面积.如图2所示.第三定律为:所有行星绕太阳一周的时间的平方与它们轨道长半轴的立方成比例.

图2 开普勒第二定律图
在静力学上,将均质细杆过焦点倾斜放入光滑的椭圆内壁中,细杆受力平衡(且该平衡状态还是稳定平衡状态)[2],如图3所示,这是细杆在光滑椭圆内壁中的平衡规律,以下简称细杆平衡规律.
下面将对这3种物理规律进行相互推导,探求规律表象之下的本质.

图3 细杆平衡规律图
1 用细杆平衡规律推导光线反射规律
细杆平衡规律为:将均质细杆过焦点倾斜放入光滑的椭圆内壁中,细杆受力平衡.
设椭圆的方程为

式中,a是椭圆的半短轴,b是椭圆的半长轴,c是椭圆的半焦距.
把一根细杆过椭圆焦点放置于椭圆内壁中,此时细杆的直线方程为

设直线与椭圆的交点为A和B,L1和L2分别为椭圆在点A和B处的法线,点C为椭圆的上焦点,连接AC和BC,如图4所示,设点A(x1,y1),点B(x2,y2),点C(x3,y3),有x3=0,y3=c.图中点Q

图4 用细杆平衡规律推导光学反射规律图

联立式(3)~式(6)得

又有三角形的内心坐标公式[3]

式中A=|BC|,B=|AC|,C=|AB|,由椭圆的第二定义得

联立式(3),式(8)和式(9),可得ΔABC内心坐标为

即Q点横坐标纵坐标都与P点一样,则Q点与P点重合,则点M,N,Q,P四点重合,又因为三角形的内心只有一个,所以Q点就是ΔABC的内心,所以有法线L1平分∠CAB,法线L2平分角∠CBA,即光线反射规律得证.
2 用光线反射规律推导细杆平衡规律
由光线反射规律知:从椭圆一个焦点发出的光线经椭圆壁反射后,反射光线都汇聚到椭圆的另一个焦点上.
把一根细杆过椭圆焦点倾斜放置于光滑椭圆内壁中,设直线与椭圆的交点为A和B,L1和L2分别为椭圆在点A和B处的法线.点C为椭圆的上焦点,如图5所示,设点A(x1,y1),点B(x2,y2),点C(x3,y3),有x3=0,y3=c.由光线反射规律知,法线L1是∠CAB的角平分线,法线L2是∠CBA的角平分线,所以法线L1和L2的交点是ΔABC的内心,设为点Q,由三角形内心的坐标公式[3]

式中A=|BC|,B=|AC|,C=|AB|,联立式(3)、式(9)、式(11),可得


图5 用光线反射规律推导细杆平衡规律图
细杆在A和B两处所受的约束力的作用线和自身重力的作用线交于点Q,由三力平衡汇交定理可知,细杆此时处于平衡状态,细杆平衡规律得证.
3 用开普勒第二定律推导光线反射规律
设椭圆的极坐标方程为
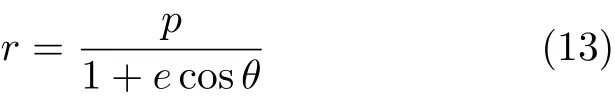
式中r为极径,θ为极角,p为椭圆的半通径,e为椭圆的离心率.如图6所示,图中A点为太阳所在位置,是椭圆的一个焦点,B点为行星的位置,是椭圆上任意一点,此时行星的速度设为v.直线BH为椭圆在点B处的法线,作直线BD使得∠DBH=∠ABH,并交极轴于点D.
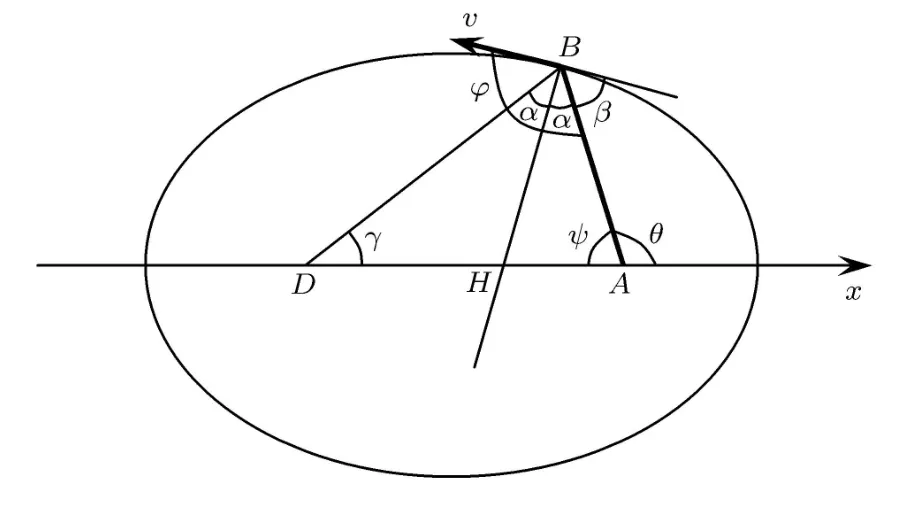
图6 用开普勒第二定律推导光线反射规律图
由开普勒第二定律可知:太阳到行星所在位置的连线在相等的时间内扫过相同的面积,即

设a为椭圆的半长轴,b为椭圆的半短轴,c为椭圆的半焦距,行星在近日点速度为v1,在远日点速度为v2,太阳的质量为M,行星质量为m,万有引力常数为G,由能量守恒定律有

由开普勒第二定律有

联立式(15)和式(16),可得

将式(17)代入式(15),可得总能量为

联立式(14)、式(16)、式(17),可得
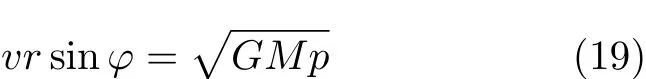
又由能量守恒定律求得行星在椭圆轨道上任意一点处的速度为

将式(13),式(20)代入式(19),并整理得

设D点到A点之间的距离为I,由正弦定理,有
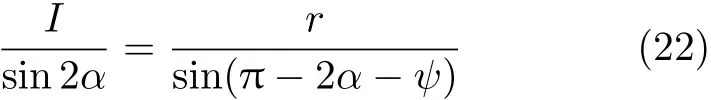
由图中几何关系可得

将式(23)代入式(22),整理可得

即D和A两点之间的距离为焦距2c,所以D点为另一个焦点,因为直线BH既是椭圆在点B处的法线,又是∠ABD的角平分线,所以光线反射规律得证.
4 用光线反射规律推导开普勒第二定律
光线反射规律为:从椭圆一个焦点发出的光线经椭圆壁反射后,反射光线都汇聚到椭圆的另一个焦点上.如图7所示,光线AB经椭圆壁反射后,反射光线BC通过椭圆的另一个焦点,该焦点设为点C.

图7 用光线反射规律推导开普勒第二定律图
对图中ΔABC,由余弦定理,有

又可得

由极坐标下的曲率半径公式

将式(13)求导并代入式(27),整理得

由万有引力定律和牛顿第二定律,有

解之得

联立式(26)、式(30)得
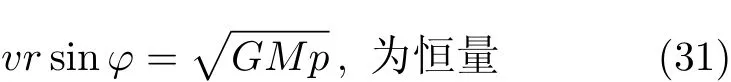
即开普勒第二定律得证.综上所述,可知光线反射规律、开普勒第二定律、细杆平衡规律三者是等价的.
5 结论
物理规律是物理现象、物理过程在一定条件下必然发生、发展和变化的规律,它反映了物质运动变化的各个因素之间的本质联系,揭露了事物本质属性之间的内在联系,任何客观规律只能被发现,不能被创造,但不同学科的规律被认识与发现的途径又是不尽相同的,本文所提到的3个物理规律,它们虽属于不同的学科范畴,但是这3个物理规律的本质都是椭圆所特有的几何特征(形状),它们只是这一本质在不同领域的不同表现,正如电场与磁场一样,它们都是电磁场在不同环境下的不同表现,又如微观粒子的波动性与粒子性,它们只不过是微观粒子在不同条件下的不同表现罢了,真是“如云表象千般变,寻得源头终归一”.
致谢感谢本刊多位编委老师对本文题目和相应内容提出的修改建议.
1阿波罗尼奥斯.圆锥曲线论.朱恩宽等译.陕西:陕西科学技术出版社,2007
2徐康.圆锥曲线的静力学性质.力学与实践,2014,36(5):639-646
3黄汉生,张述松.计算三角形五心坐标的统一公式,数学教学研究,1991,10(4):23-25
(责任编辑:胡漫)
O31
A
10.6052/1000-0879-16-265
2016–08–15收到第1稿,2016–10–06收到修改稿.
1)2014年湖北省高等学校省级教学研究资助项目(2014241).
徐康,刘章军.透过椭圆焦点看物理规律.力学与实践,2017,39(2):210-214 Xu Kang,Liu Zhangjun.Comprehending the laws of physics through elliptical focus.Mechanics in Engineering, 2017,39(2):210-214

