单裂缝中携砂液流动规律研究1)

李鹏苏建政张岩†,张旭辉†,,鲁晓兵†,(页岩油气富集机理与有效开发国家重点实验室，北京100083)

†(中国科学院力学研究所，北京100190)

∗∗(中国科学院大学，北京100049)

单裂缝中携砂液流动规律研究1)

李鹏∗,†,∗∗苏建政∗张岩†,∗∗张旭辉†,∗∗,2)张旭辉，副研究员，主要从事水合物开采相关关键力学问题研究.E-mail:zhangxuhui@imech.ac.cn鲁晓兵†,∗∗∗(页岩油气富集机理与有效开发国家重点实验室，北京100083)

†(中国科学院力学研究所，北京100190)

∗∗(中国科学院大学，北京100049)

裂缝中携砂液流动是一种固液两相流，携砂液的运移与支撑剂的铺置是水力压裂裂缝保持导流能力的关键.本文基于FLUENT流体计算软件，采用双流体模型，将颗粒看作拟流体，携砂液按照牛顿流体处理，分析了支撑剂体积分数αs、阿基米德数Ar、颗粒雷诺数Re以及裂缝入口边界对流动规律的影响.研究结果表明：携砂液在裂缝中的流动过程中，发展成为支撑剂体积分数不同的四个区域，包括砂堤区、颗粒悬浮区、颗粒滚流区和无砂区；支撑剂的沉降程度随着支撑剂体积分数和阿基米德数的增加而增加，而随着雷诺数增加而降低；入口为网眼型时，进入裂缝后过流面积的增加导致流速突降，使得支撑剂更容易在入口处产生堆积，在同一入口流速下，较均匀入口的工况铺砂高度大.

携砂液，裂缝，两相流，水力压裂，数值模拟

Key wordsproppant-laden fl uid，fracture，two phase fl ow,hydraulic fracturing,numerical simulation

页岩油气为非常规能源之一.通过水力压裂获得连通的裂缝网络系统是实现这种高储量、微孔低渗透岩层中油气开采的关键技术.油气开采过程中，由于压力的降低，在地应力作用下，这些裂缝会逐渐减小甚至闭合，导致压裂失效[1].工程中，一般通过井口向地层中注入高黏度的流体和支撑剂(之后称为携砂液)，裂缝中携砂液运移以及支撑剂的铺置，使得在油气开采降压过程裂缝不至闭合，从而提高页岩油气的有效体积改造范围.压裂裂缝的流体传导能力取决于携砂液在裂缝中的运移距离与支撑剂的铺置范围.

页岩油气储层经人工压裂后会形成复杂的裂缝网络[2],裂缝网络中携砂液流动过程非常复杂，受到复杂的裂缝几何形态与网络系统结构,支撑剂颗粒粒径与形状,支撑剂的密度,携砂液黏度、压力、温度、流量,支撑剂体积分数等多种参数的影响[34].这些参数的变化又改变其流动特征，比如浓度和黏度的增加，使得携砂液从牛顿流体向非牛顿流体转变；流速的增加使得流动从层流向湍流改变[45].

目前，国内外学者主要是针对单裂缝中携砂液的流动规律取得了一些认识.沉降和对流是控制铺砂形态的两大机理.针对单颗粒在流体中运动的力学机制已经有了较为成熟的认识[67]，但颗粒群在流体中的运动规律，尤其是颗粒碰撞、固液两相相互作用等尚未研究清楚，比如阻力系数公式完全不同于单颗粒运动的公式[8].携砂液进入裂缝中时，支撑剂的速度在缝高方向上不同，从而产生浓度的差异，浓度差引起支撑剂的对流运动.对流和沉降分别取决于裂缝宽度和颗粒直径[911].

在低黏度流体条件下，携砂液的运动速度是支撑剂沉降的关键影响参数，支撑剂的沉降会在裂缝底部形成砂堤，减小了裂缝的过流面积，提高上部流体的流动速度，砂堤的增长和其上方的流速最终达到一个动态平衡[12].Dontsov等[13]提出了考虑重力沉降的支撑剂输送数学模型，该模型可以描述当支撑剂体积分数升高时携砂液在裂缝中由泊肃叶流动到达西流动的转变.结果表明：颗粒会在裂缝的中间部位形成聚集；对于高浓度携砂液来说，液体速度分布将会偏离经典的抛物线形状.

Shiozawa等[14]利用支撑剂输送数学模型，基于全三维水力压裂模拟软件CFEAC[1516]进行了支撑剂输送的数值模拟，考虑了支撑剂的重力沉降、端部脱砂和裂缝闭合的全过程.结果表明：支撑剂过早沉降和端部脱砂不利于形成良好的支撑剂铺置效果；支撑剂会在自然裂缝和水力压裂裂缝的交叉点处产生聚集.在页岩油气水力压裂体积改造工程中，往往进行多参数的调整以满足实际工况的需求，但目前的这些研究工作缺乏系统的参数分析.国内孙海成[17]通过理论推导获得了脆性页岩裂缝网络中支撑剂沉降的控制参数，李靓[18]针对裂缝中携砂液运移与支撑剂沉降特性进行了实验研究，初步分析了交叉裂缝中支撑剂密度、流体速度和黏度等对携砂液流动的影响.

FLUENT是一款高效的流体力学计算软件，可以模拟从不可压缩到高度可压缩范围内的复杂流动[19]，其主要特点是采用多重求解方法和多重网格加速收敛技术.灵活的非结构化网格和基于解的自适应网格技术，使其在多相流、化学反应与燃烧、材料加工等领域得到广泛应用.

鉴于此，本文基于FLUENT软件，采用双流体计算模型，将支撑剂颗粒看作拟流体，开展支撑剂体积分数、阿基米德数、雷诺数三个无量纲控制参数的敏感性分析，获得携砂液流动与支撑剂沉降的基本特征，为页岩油气储层体积改造提供参考依据.

1 双流体模型

裂缝中携砂液的流动是典型的固液两相流动问题，本文利用FLUENT软件，采用双流体模型进行模拟计算，将颗粒相看作拟流体进行处理，利用颗粒动理学理论作为封闭方程，求解两相的质量、动量守恒方程及颗粒拟温度方程，并引入湍流模型.

1.1 质量和动量守恒方程

液相和固相的连续性方程[20]

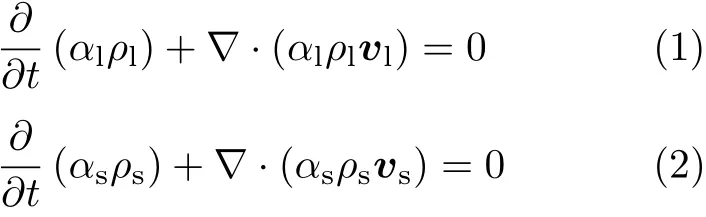
其中,α为体积分数；ρ为密度，kg/m3；v为速度，m/s；下标l，s分别代表液相和固相.液相和固相的体积分数之和必须等于1.

液相和固相的动量守恒方程

其中P为液相压力，Pa；Ps为固相压力，Pa；τl和τs分别为液相和固相的剪切应力张量，Pa；g为重力加速度，g=9.81m/s2；Ksl为相间动量交换系数，kg/(m3·s).

液相和固相的剪切应力张量分别为

其中µl和µs为剪切黏度，Pa·s；λl和λs为体积黏度，Pa·s；I是二阶单位张量.

固相的剪切黏度由碰撞黏度、动理黏度和摩擦黏度三部分组成：

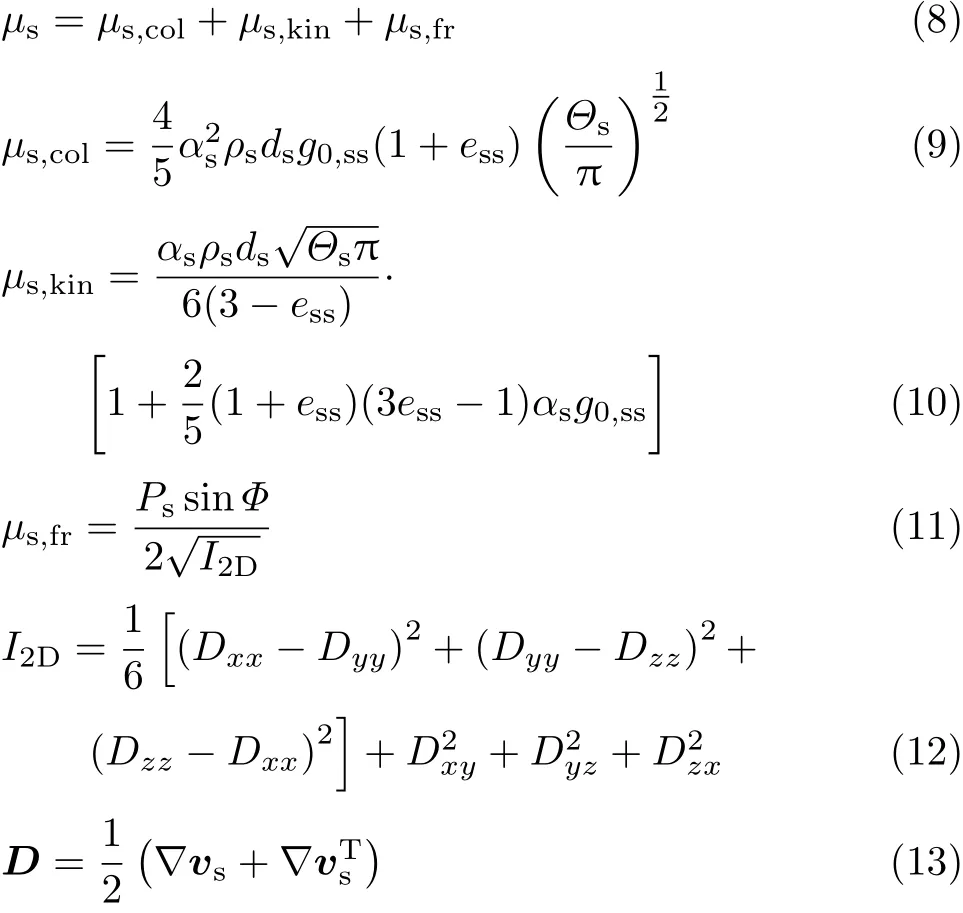
其中µs,col为固相碰撞黏度，Pa·s，采用Gidaspow模型；µs,kin为固相动理黏度，Pa·s，采用Syamlal模型；µs,fr为固相摩擦黏度，Pa·s，采用Schae ff er模型；ds表示颗粒的直径，m；ess为颗粒碰撞恢复系数，默认为0.9；g0,ss为径向分布函数；Θs为颗粒拟温度，m2/s2；Φ为内摩擦角，rad，取π/6；I2D为偏应力张量常数；D为固相的应变张量，s−1,其分量为Dij,i,j=x,y,z.

液相的体积黏度假设为0，固相体积黏度采用了Lun模型

固相压力表示单位时间内通过单位面积交换的颗粒动量，即颗粒法向应力，采用Lun模型

径向分布函数是一个当固体颗粒相变密时用于修改颗粒之间碰撞概率的修正因子，FLUENT软件中采用的计算模型为

其中αs为颗粒体积分数；αs,max为颗粒最大体积分数，FLUENT软件默认值为0.63.

相间作用力采用Gidaspow提出的曳力模型，在此模型中，相间动量交换系数表示为

其中CD为相间动量交换阻力系数；Res为以相间滑移速度定义的雷诺数.

1.2 颗粒拟温度方程

固相的颗粒拟温度是与颗粒的随机运动的动能成比例的，从动能理论得到的输运方程表示为[21]

其中γΘs为颗粒碰撞造成的能量耗散，kg/(m·s3)，采用Lun理论表示为

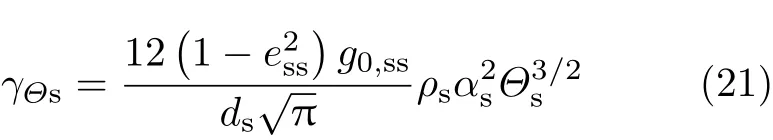
Φls为固液两相的能量交换，kg/(m·s3)，表示为

kΘs为能量扩散系数，kg/(m·s)，采用Gidaspow模型表示为

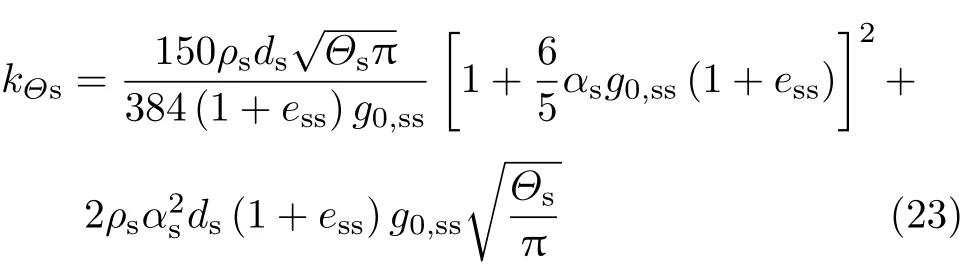
对于颗粒相，壁面上的剪切力采用下面的形式

其中Us,‖为平行于壁面的颗粒滑移速度，m/s；ϕ为颗粒与壁面之间的反射系数，取为0.01.

1.3 湍流方程

湍流模型使用重整化群k--ε模型，其湍动能与耗散率方程为

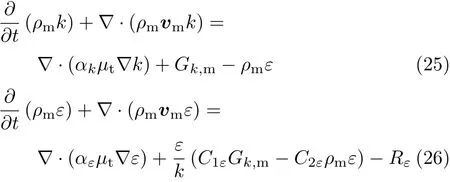
2 单裂缝中携砂液流动特征分析

2.1 几何建模与边界条件

几何构建与网格划分主要通过FLUENT的前处理软件GAMBIT来完成.将裂缝简化为只考虑长度和高度方向的二维平面模型，如图1所示.本文中建立了两种模型，分别为均匀入口模型与网眼入口模型.裂缝尺寸2000mm×300mm，对于网眼入口设置为10个网眼孔，高度10mm，模型裂缝内的流动区域设定为“Fluid”.考虑到模型裂缝为规则的矩形结构且长度方向尺寸较大，网格尺寸设定为4mm×3mm，长度方向500格，高度方向100格，采用四边形结构网格类型，对几何模型划分网格，整个几何模型共划分网格数为5万个.模拟中定义左侧边界为速度入口边界，且固体速度与液体速度相等.右侧边界为压力出口边界，其他边界为壁面.壁面采用无滑移边界条件.

图1 模型几何结构及边界条件设置

2.2 数值方法及参数选取

选择基于压力的求解器，离散格式为二阶迎风格式，压力速度耦合选择Phase-coupled SIMPLE算法求解.时间步长取为0.001s，每一时间步长最大迭代次数取50次.入口湍流模型选用重整化群k--ε模型，采用下面的经验公式计算湍流强度和湍流尺度

入口颗粒拟温度值设置为10−5m2/s2.颗粒拟温度表示的是颗粒湍动的动能，与颗粒由于相互碰撞产生的随机运动的动能成比例.在入口处，支撑剂和携砂液以相同的速度注入裂缝，支撑剂之间不发生相互碰撞，此时可认为入口处的颗粒拟温度值为0，但是为了使颗粒拟温度方程易于收敛，需要在入口处给颗粒拟温度设置一个非常小的初值.

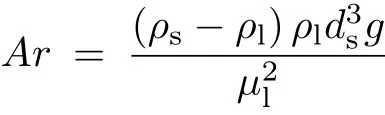
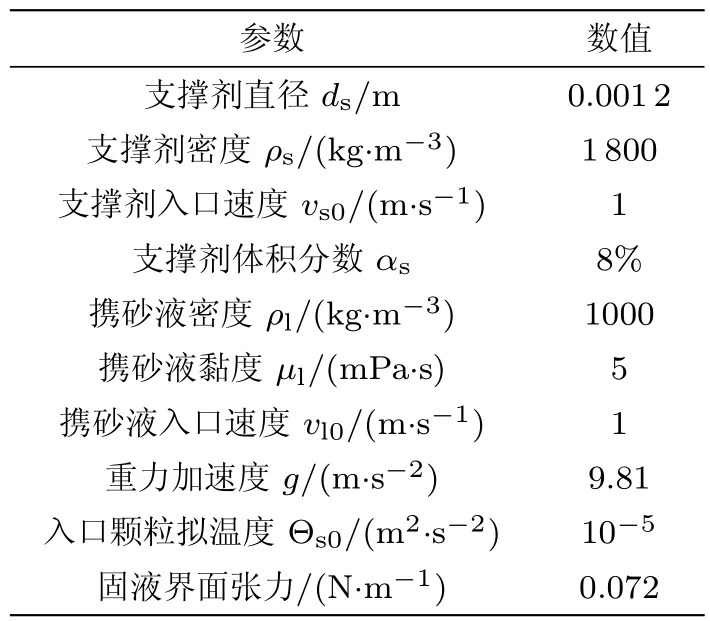
表1 数值模拟参数设置

2.3 携砂液流动计算结果分析

2.3.1 基本现象

携砂液体进入裂缝以后，颗粒受到水平方向液体的携带力、垂直向上的浮力、垂直向下的重力、颗粒沉降阻力的共同作用.一定时间后，颗粒沉降形态最终趋于稳定.当使用低黏度的携砂液时，由于颗粒所受到的黏滞阻力相对较小，颗粒下沉速度就会较快，沉到裂缝底部形成砂堤.砂堤的形成会减小携砂液的过流横截面积，提高了流体的流动速度.当流速足够大的时候，支撑剂颗粒处于悬浮状态(颗粒沉降速度为零)，此时支撑剂颗粒沉积与卷起处于动平衡状态.平衡状态对应的液体速度称为平衡流速，对应的砂堤最大高度称为砂堤平衡高度(用Heq来表示).此时根据支撑剂的体积分数在缝高上的分布将流动区域分成4个分区[18]:Ⅰ区(砂堤区)是支撑剂在输送过程中沉降到裂缝底部堆成的砂堤区域；Ⅱ区(颗粒滚流区)是支撑剂颗粒在沉降到砂堤上之前在砂堤上方滚动的区域，此时颗粒沉降与卷起处于动平衡状态；Ⅲ区(悬浮区)是支撑剂由于重力作用向下沉，但又受到液体黏性阻力的作用而悬浮的区域.这个区域内平均的支撑剂体积分数同入口处的支撑剂体积分数基本相同；Ⅳ区(无砂区)是支撑剂颗粒完全下沉，只有基液的区域.如图2所示，数值模拟的结果验证了前人在实验中发现的四个分区的现象以及平衡高度与平衡时间定义.

图2 支撑剂体积分数沿缝高分布图

2.3.2 支撑剂体积分数αs的影响

图3为体积分数为13%时网眼入口下铺砂形态随时间的变化.携砂液进入裂缝后，由于过流面积的变化，速度降低，在入口处很快形成一定高度的砂堤，这个沉降高度小于底部第一个网眼的高度，这时4个分区初步形成.之后随着携砂液的注入，支撑剂沉降的砂堤随之扩展，滚流区和悬砂区向前推移.当携砂液到达出口时，前锋的支撑剂流出，这样的过程持续到砂堤高度不再增加，即达到平衡高度.

图4和图5列出了均匀入口与网眼入口下不同体积分数(其他基本物理参数不变，变化体积分数分别为2.7%,8%,13%,18%)的最终铺砂形态.随着支撑剂体积分数由2.7%增加到18%，最终铺砂的平衡高度由9mm增加到37mm，呈递增趋势，且可以明显看出颗粒滚流区逐渐变大，悬浮区逐渐变小，同时网眼入口模型比均匀入口模型在距离入口更近的地方发生沉砂,如图4所示.主要原因是支撑剂体积分数的增加导致颗粒间的碰撞更加剧烈，从而滚流区增大.随着支撑剂体积分数变大，颗粒间的聚集效应变强，导致颗粒聚集下沉，因此平衡高度出现位置更靠近入口.

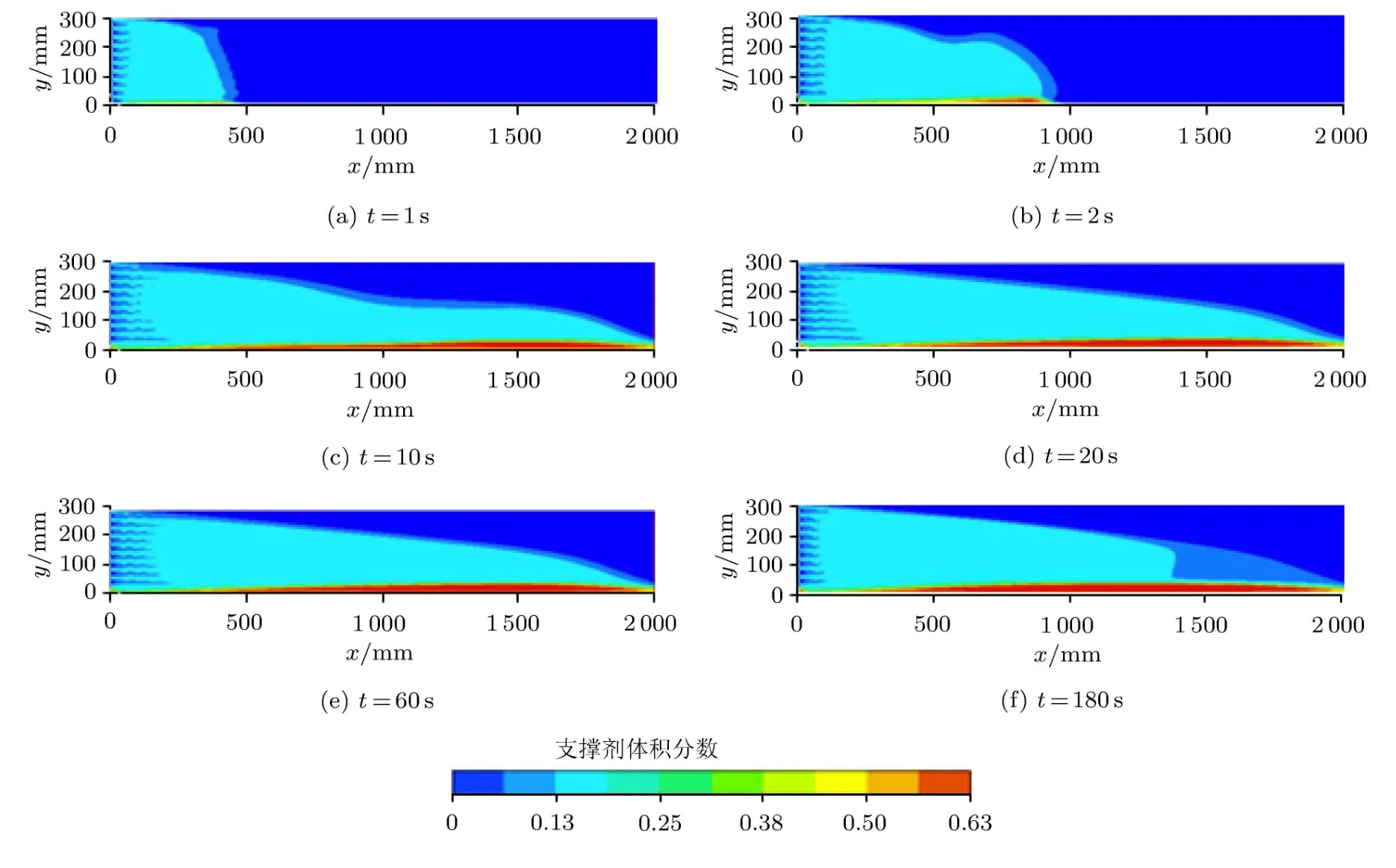
图3 αs=13%时铺砂形态随时间的变化过程

图4 网眼入口下支撑剂不同体积分数最终铺砂形态

通过对比同一体积分数不同入口类型下结果可以发现网眼入口模型的铺砂高度大于均匀入口模型，如图6所示.主要原因是携砂液进入裂缝的速度相同，对于网眼类型入口，携砂液的速度在进入裂缝后会降低(过流面积较入口增加)，因此支撑剂更容易发生沉降.

图5 均匀入口下支撑剂不同体积分数最终铺砂形态

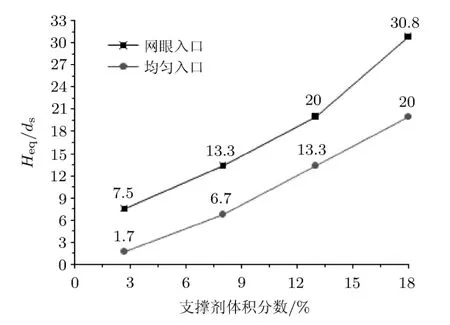
图6 不同支撑剂体积分数的平衡高度的变化

2.3.3 阿基米德数Ar的影响

阿基米德数表征两相密度差引起的对流效应.由图7和图8可以看出，当其他基本物理参数不发生变化时，改变固相密度,分别取1100kg/m3, 1334kg/m3,1567kg/m3,1684kg/m3,1800kg/m3,阿基米德数由68增加到542，可以明显发现支撑剂的沉降更明显，平衡高度的出现位置距入口更近，平衡高度由2mm增加到16mm，呈递增趋势.在较小阿基米德数下，最终铺砂达到平衡高度所用的时间更长.同时阿基米德数增大导致支撑剂输送悬浮区变小.在较大的阿基米德数下，颗粒悬浮的范围很大；而在较小的阿基米德数下，颗粒悬浮区的范围很小.图9显示的是在Ar=384时铺砂状态的一个演变过程.

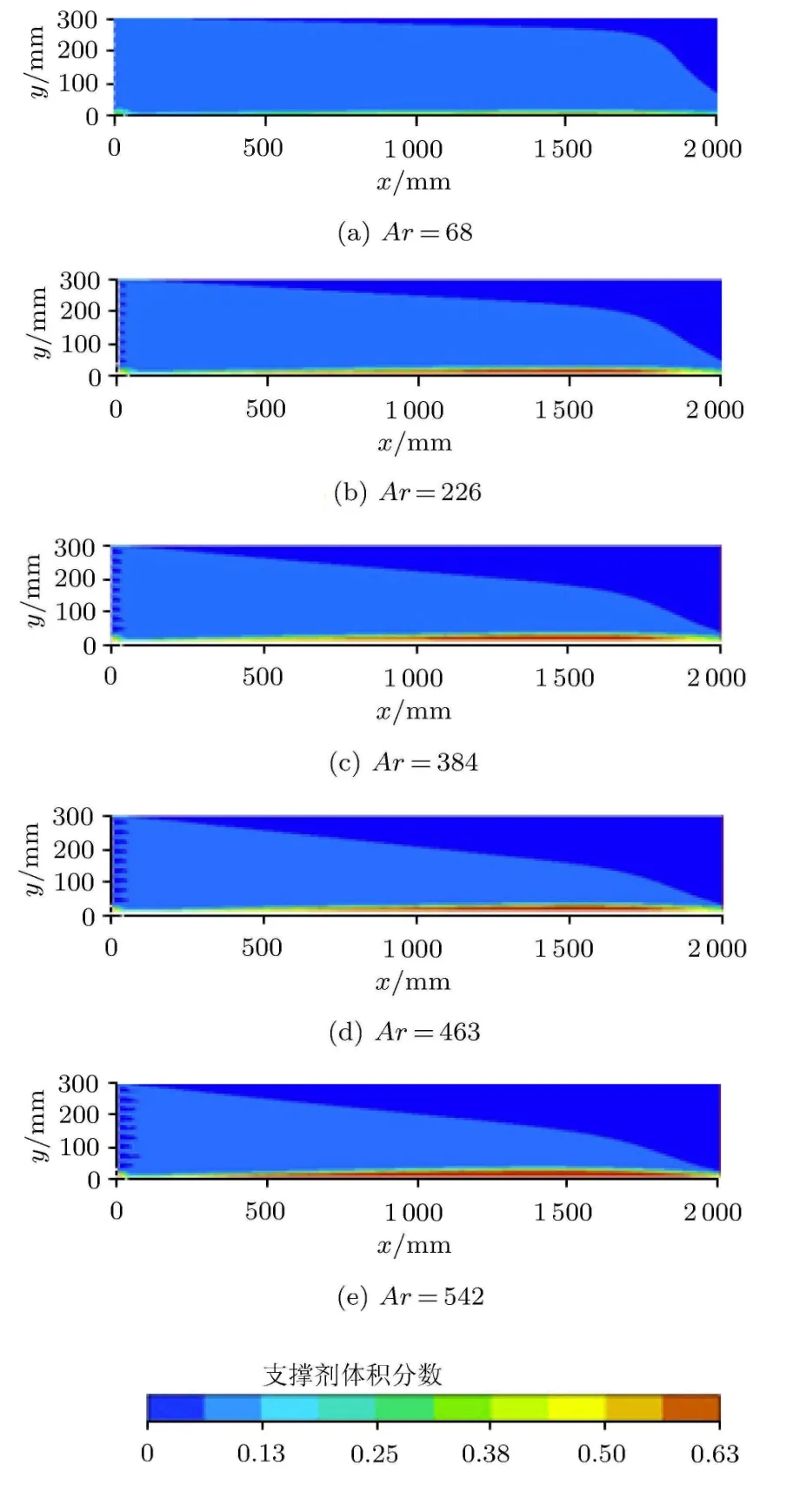
图7 不同阿基米德数下最终铺砂形态

图8 不同阿基米德数下平衡高度的变化

原因主要是保持体积分数和雷诺数不变时，阿基米德数增加相当于支撑剂的重力沉降效应变得更大，支撑剂沉降变快，因此平衡高度增加，平衡高度出现位置离入口更近.

2.3.4 雷诺数Re的影响

雷诺数表征的是惯性效应与黏性效应的比值.由图10和图11可以看出，当其他基本物理参数不发生变化时，改变携砂液注入速度，分别取1m/s, 1.5m/s,2m/s,2.5m/s,3m/s，雷诺数由240增加到720，砂堤的平衡高度由45mm下降到14mm，并且砂堤平衡高度出现的位置出现明显远离入口位置的趋势，而且随着雷诺数增加，最终铺砂达到平衡高度所用的时间也更长.此外，还可以观察到雷诺数递增以后，砂堤区逐渐变小，颗粒滚流区逐渐变大.图12显示的是在Re=240时铺砂状态的一个演变过程.

图9 Ar=384时铺砂形态随时间的变化过程

出现这种状况的原因是由于在保持阿基米德数和砂子体积分数不变的情况下，随着雷诺数的增加，携砂液的水平携砂能力增强，惯性效应变大，入口处湍流效应更明显，支撑剂不断被卷起然后输送到远处，所以沉降位置明显远离入口，而且平衡高度变小.

图10 不同雷诺数下的最终铺砂形态

图10 不同雷诺数下的最终铺砂形态(续)

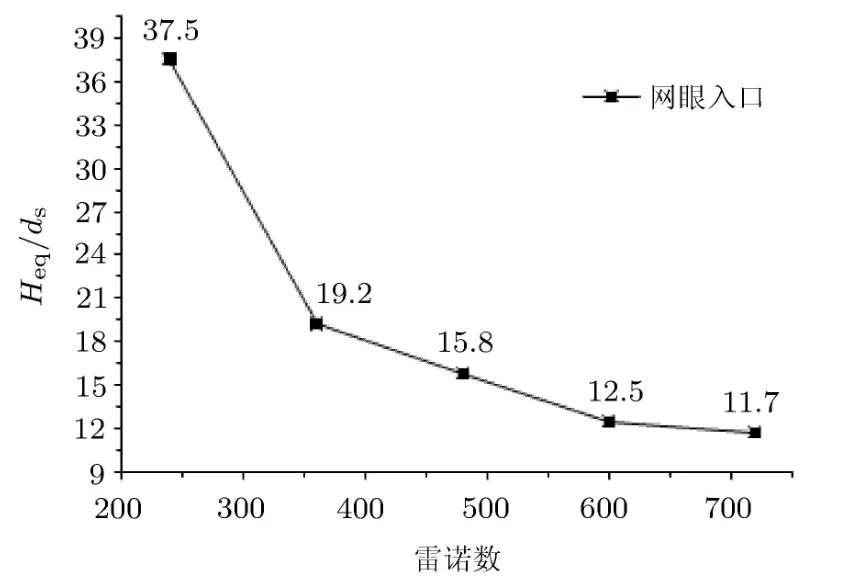
图11 不同雷诺数下平衡高度的变化

3 结论

裂缝中携砂液的流动是典型的固液两相流动问题，本文利用FLUENT流体力学计算软件，采用双流体模型进行模拟计算，将颗粒相看作拟流体进行处理，利用颗粒动理学理论作为封闭方程，研究了单裂缝中携砂液的流动规律.影响携砂液流动的因素众多，主要包括裂缝性质、支撑剂性质、携砂液性质以及施工条件等.以往的研究中都是对其中的某一个物理量的影响进行分析，比如入口速度、携砂液的黏度、支撑剂直径及密度，但携砂液的流动规律往往都是受到各种因素的综合影响，单个物理量的敏感性分析无法准确描述携砂液的流动和支撑剂的铺置规律.本文在量纲分析的基础上，通过数值模拟的方法，获得了单裂缝中携砂液流动的基本物理过程和基本数据，得到了支撑剂体积分数、阿基米德数、雷诺数三个无量纲数对携砂液流动的影响规律.在衡量最终的铺砂效果时，借鉴前人的研究成果，用平衡高度和平衡时间来进行衡量.

取得的主要结论如下：

(1)不同的裂缝入口方式对裂缝中的铺砂形态会有显著影响，同一排量下，网眼入口的铺砂高度大于均匀入口的铺砂高度，同时网眼入口模型比均匀入口模型在距离入口更近的地方发生沉砂；

(2)随着支撑剂沉降形成砂堤高度的增加，支撑剂在裂缝中的流动达到平衡，此时称作砂堤平衡高度.根据支撑剂的体积分数在缝高上的分布将流动区域分成四个分区：砂堤区、颗粒滚流区、悬浮区、无砂区.

(3)随着支撑剂体积分数的增加，最终铺砂的平衡高度呈现递增的趋势，颗粒滚流区逐渐变大，悬浮区逐渐变小；随着阿基米德数的增加，支撑剂的沉降更明显，平衡高度的位置向入口处移动，最终铺砂达到平衡高度所用的时间更长；随着雷诺数的增加，砂堤的平衡高度下降，并且砂堤平衡高度出现的位置与入口位置之间的距离呈现明显增大的趋势.

本文的模拟未考虑流体滤失、裂缝三维效应、复杂裂缝网络结构等物理参数，将在进一步研究工作中深入分析.

图12 Re=240时铺砂形态随时间的变化过程

1张广明,刘勇,刘建东等.页岩储层体积压裂的地应力变化研究.力学学报,2015,47(6):965-972

2曾青冬,姚军,孙致学.页岩气藏压裂缝网扩展数值模拟.力学学报,2015,47(6):994-999

3温庆志,翟恒立,罗明良等.页岩气藏压裂支撑剂沉降及运移规律实验研究.油气地质与采收率,2012,19(6):104-107

4黄志文,苏建政,龙秋莲等.基于Fluent软件的携砂液流动规律模拟研究.石油天然气学报,2012,34(11):123-125

5 Eissa ME,Shokir KS,Abdulrahman AA.Experimental and numerical investigation of proppant placement in hydraulic fractures.SPE-107927-MS,2007

6刘大有.二相流体动力学.北京:高等教育出版社,1993

7王光谦,倪晋仁.颗粒流研究评述.力学与实践，1992,14(1): 7-19

8 VanderhoefMA,BeetsraR,KuipersJAM.Lattice-Boltzmann simulations of low-Reynolds-number fl ow past mono-and bi-disperse arrays of spheres:results for permeability and drag force.Journal of Fluid Mechanics,2005, 528:233-254

9 Cleary MP,Fonseca A.Proppant convection and encapsulation in hydraulic fracturing:practical implications of computer and laboratory simulation.SPE-24825-MS,1992

10 Abdulrahman A.Dimensionless groups for interpreting proppant transport in hydraulic fractures.Management&Production Engineering Review,1999,357(2):324-335

11 Clear P,Wright CA,Wright TB.Experiment and modeling evidence for major changes in hydraulic fracturing design and fi eld procedures.SPE-21994-MS,1991

12 Kern LR,Perkins TX,Wyant R.E.The mechanics of sand movement in fracturing.Journal of Petroleum Technology, 1959,11(7):55-57

13 Dontsov E,Peirce A.Slurry fl ow,gravitational settling and a proppant transport model for hydraulic fractures.Journal of Fluid Mechanics,2014,760:567-590

14 Shiozawa S,McClure M.Simulation of proppant transport with gravitational setting and fracture closure in a three-dimensional hydraulic fracturing simulator.Journal of Petroleum Science and Engineering,2016,138:298-314

15 McClure M,Home RN.Discrete Fracture Network Modeling of Hydraulic Stimulation:Coupling Flow and Geo-Mechanics.Berlin:Springer,2013

16 McClure WM,Babazadeh M,Shiozawa S,et al.Fully coupled hydro-mechanical simulation of hydraulic fracturing in 3D discrete fracture networks.SPE-173354-PA,2016

17孙海成.脆性页岩网络裂缝中支撑剂的沉降特性.油气地质与采收率,2013,20(5):107-110

18李靓.压裂缝内支撑剂沉降和运移规律实验研究.[硕士论文].成都：西南石油大学,2014

19金俊卿,郑云萍.FLUENT软件在油气储运工程领域的应用.油气储运,2013,31(2):27-30

20 Anderson TB,Jackson R.A fl uid mechanical decription of fl uidized beds.Industrial&Engineering Chemistry Fundamentals,1967,6:527-539

21 Gidaspow D.Multiphase fl ow and fl uidization:continuum and kinetic theory description.Boston:Academic Press, 1994

22 Tan QM.Dimensional analysis:with case studies in mechanics.Berlin,Heidelberg:Springer-Verlag Berlin Heidelberg,2011

(责任编辑:胡漫)

THE TWO PHASE FLOW OF PROPPANT-LADEN FLUID IN A SINGLE FRACTURE1)

LI Peng∗,†,∗∗SU Jianzheng∗ZHANG Yan†,∗∗ZHANG Xuhui†,∗∗,2)LU Xiaobing†,∗∗∗(State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and E ff ective Development,Beijing 100083,China)
†(Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China)
∗∗(University of Chinese Academy of Sciences,Beijing 100049,China)

The fl ow of the proppant-laden fl uid in fractures is a two phase fl ow.The migration of the proppant laden fl uid and the transportation and the arrangement of the proppant in the fracture are the key to keep the fl ow conductivity in the fracture.Based on the FLUENT software for the fl uid mechanics,the two- fl uid model is adopted,and the solid phase and the liquid phase are regarded as the pseudo- fl uid and the newtonian fl uid,respectively.The e ff ects of the proppant volume fraction,theArnumber,theRenumber,and the inlet boundary on the fl ow are investigated.It is shown that four di ff erent zones are developed with di ff erent volumetric fractions,including the sand bank zone,the sand tumble zone,the sand suspension zone,and the sand free zone.The thickness of the settled proppants increases with the increase of the proppant concentration and theArnumber,while it decreases with the increase of theRenumber.Under the condition of the mesh type boundary,the accumulation of the proppants occurs at the inlet due to the sudden increase of the fl ow area.

TE348

A

10.6052/1000-0879-16-284

2016–09–01收到第1稿，2016–11–11收到修改稿.

1)页岩油气富集机理与有效开发国家重点实验室开放基金(G5800-15-ZS-WX047)资助项目.

李鹏,苏建政,张岩等.单裂缝中携砂液流动规律研究.力学与实践,2017,39(2):135-144 Li Peng,Su Jianzheng,Zhang Yan,et al.The two phase fl ow of proppant-laden fl uid in a single fracture.Mechanics

in Engineering,2017,39(2):135-144