一类二自由度系统振动的黄金分割率1)
朱贝贝孙兰宁赵忠虎∗
∗(兰州大学土木工程与力学学院,兰州730000)
†(中航勘察设计研究院有限公司,北京100098)
∗∗(亚利桑那大学工程学院,美国图森AZ85721)
一类二自由度系统振动的黄金分割率1)
朱贝贝∗,2)朱贝贝,硕士,主要从事岩石力学与结构力学等方面的研究工作.E-mail:zhubei1991@yeah.net孙兰宁†赵忠虎∗,∗∗,3)赵忠虎,博士,副教授,主要从事岩石力学与结构力学等方面的研究工作.E-mail:zhaozhh@lzu.edu.cn
∗(兰州大学土木工程与力学学院,兰州730000)
†(中航勘察设计研究院有限公司,北京100098)
∗∗(亚利桑那大学工程学院,美国图森AZ85721)
作为数学史上一个重要的比例关系,黄金分割理论已在美学、建筑学甚至工程学中发挥了一定的作用.为了研究一类二自由度系统振动的黄金分割效应,首先介绍了黄金分割的基本理论,然后分别分析了该类二自由度体系的自由振动特征,以及简谐载荷作用下受迫振动的共振机制.结果表明,结构圆频率与层刚度和质量之比、两结构质点振幅之比都符合黄金分割率,结构在振动中具有和谐之美.
结构动力学,黄金分割,二自由度,自由振动,受迫振动
黄金分割率是数学上的一个比例关系,它古老而又神奇.最早论述黄金分割率的著作,为公元前300年欧几里得撰写的《几何原本》,该书详细论述了黄金分割率的算法.现阶段,黄金分割率多与美学[1]、建筑学[2]、力学[3]、工程学[4]等领域结合在一起,渗透到我们的日常生活中.
中世纪意大利数学家莱昂纳多·斐波那契提出的“斐波那契数列”,可作为符合黄金分割规律的典范.为了美观,很多国家的国旗采用线段比率符合黄金分割率的五角星图案.设计者按接近0.618的长宽比,制作门窗、书籍、电视电脑屏幕等生活用品,令人们更加舒适地使用,也是应用黄金分割率的例子.由此可见在生活中,随处都有黄金分割率的影子.
然而,学者们对于结构的黄金分割规律研究的依然很少,很多关键性问题没有得到完善.本文将针对一类特殊的二自由度系统振动下的黄金分割率进行论述,希望能对今后的相关研究带来一定的启发.
1 黄金分割基本理论
如图1所示,设直线AB被点C分割成两段,如果AC/AB=CB/AC,则C点称为直线AB的黄金分割点.

图1 黄金分割示意图
由定义可知,AC=AB×CB,令AB=1,AC=x,则有
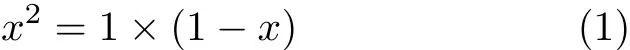
根据方程(1),可解得x≈0.618(舍去负值).
数学上,0.618被公认为最具有审美意义的比例数字,1:0.618也被为黄金比,它们共同构成了黄金分割理论的精髓.
2 二自由度系统的自由振动
研究二自由度系统的自由振动,结合工程实际对问题进行简化.工程中由于抗震的需要,结构在竖直方向的刚度、质量不能有过大变化,因此假定每层的刚度均为k,质量为m1=m2=m,模型如图2所示.
模型动力学方程为[5]
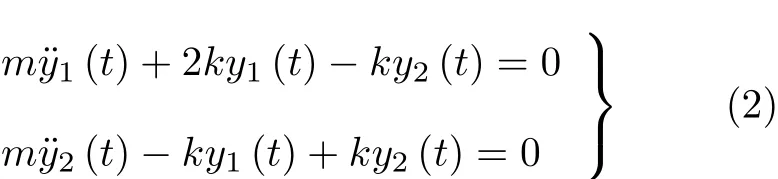
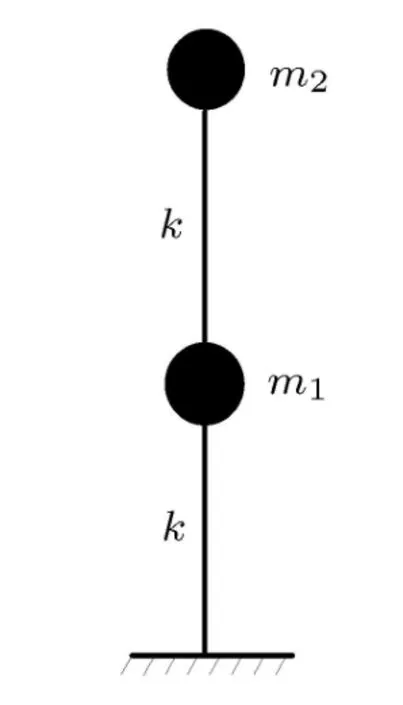
图2 自由振动模型
方程(2)的频率方程如下
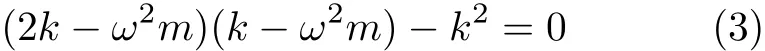
两式中,k为结构的刚度系数,yi(t)为质点振动位移,ω为自由振动圆频率.
由式(3)得
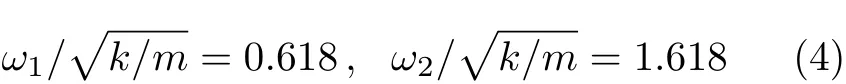
圆频率ω1,ω2分别对应的振幅的比值
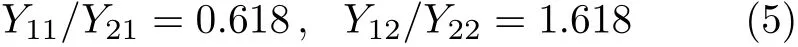
其中Yij为质点i对应频率ωj的振幅.
通过上述理论分析,二自由度系统的自由振动中,圆频率pω1与层间刚度和质量比值的平方根之比,即以及其对应的振型之比,都符合黄金分割率.对于圆频率ω2来说,这两个比值都比ω1时多1,这是个有意思的现象,今后可对此进行深入的分析,以完善该方面的研究成果.
3 二自由度系统的受迫振动
结构在现实中受到一定的侧力作用,发生受迫振动.取二自由度系统在水平振动载荷作用下的模型如图3所示.
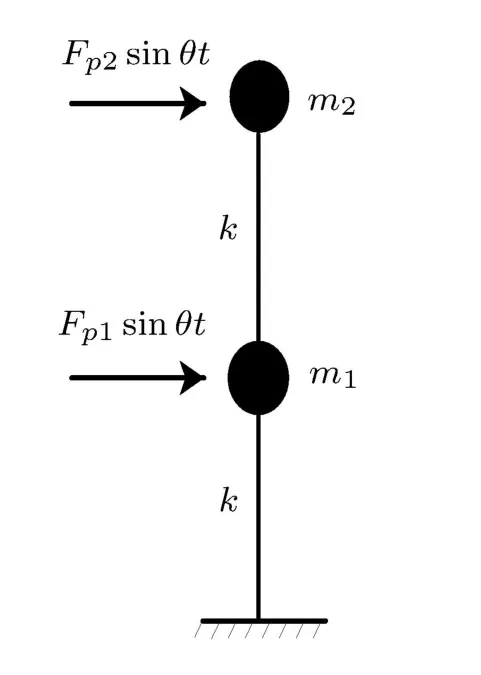
图3 受迫振动模型
每层集中质量和刚度与自由振动时的假设一致,则在简谐水平载荷Fpisinθt作用下的动力学方程为
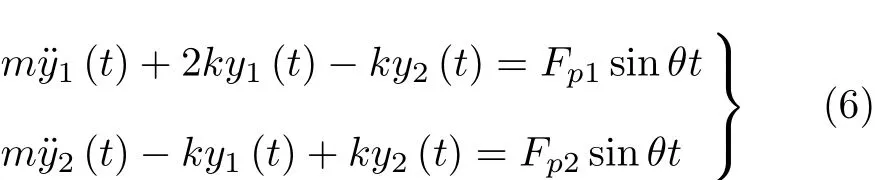
由此得位移振幅为
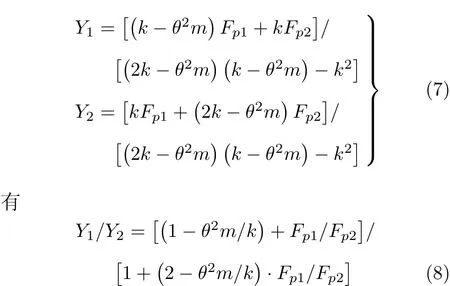
当θ=ω,即结构自振频率等于外载荷的频率时,结构将发生共振.结合条件θ=ω1与式(4),代入式(8)可得
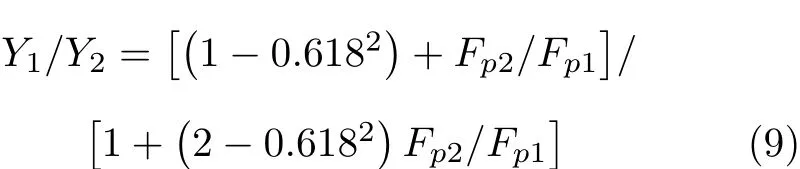
分别赋予Fp2/Fp1不同的比值,将Y1/Y2值列入表1.
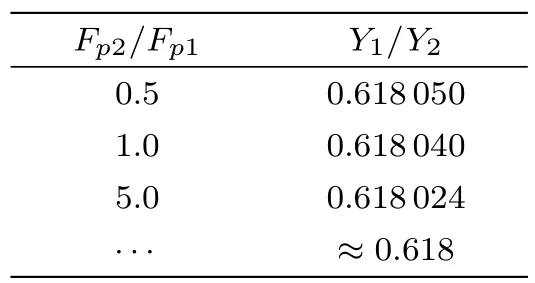
表1 Fp2/Fp1比值下的Y1/Y2
从表1不难发现,无论Fp2/Fp1为何值,Y1/Y2都约为0.618这一黄金分割数,且有Fp2/Fp1越大,Y1/Y2越接近0.618的趋势.
以上研究可见,二自由度系统在简谐载荷作用下发生共振,质点振幅之比符合黄金分割率,并与作用于每层上的外载荷没有直接关系.
4 结论
通过分析一类二自由度系统的自由振动以及在简谐载荷作用下的受迫振动特征,得出如下结论:
(1)该类二自由度系统在自由振动中,其振动圆频率与每层的刚度和质量比值的平方根之比,以及对应的振幅之比,均符合黄金分割率.
(2)该系统在简谐载荷作用下发生共振时,两质点的振幅之比符合黄金分割率,并且与质点所受载荷幅值无关.
综上所述,黄金分割率存在于结构的振动体系中,并表现出规律性.然而,本文仅针对某类“特殊的二自由度系统”进行研究,关于二自由度系统的普遍情况,还需进一步分析.另外,此现象的实际利用,比如结构的优化设计以及工程抗震设计,将是今后研究工作的重点.
1陈翠花,邵丁.对黄金分割及其教育意义的思考.数学教育学报,2006,15(4):21-23
2 Bangs H.宗教建筑学的回归——黄金分割率与现代主义的衰落.北京:电子工业出版社,2013
3董天立,韩增盛.力学中的黄金分割率,力学与实践,2008, 30(5):112-113
4李长冬,胡新丽,汤旻烨等.二维黄金分割法在抗滑桩截面优化设计中的应用.地质科技情报,2007,26(5):91-94
5王伟,赖永星,苗同臣.振动力学与工程应用.郑州:郑州大学出版社,2008
(责任编辑:胡漫)
THE GOLDEN SECTION RATIO OF A CLASS OF VIBRATION SYSTEM OF TWO DEGREES OF FREEDOM1)
ZHU Beibei∗,2)SUN Lanning†ZHAO Zhonghu∗,∗∗,3)
∗(School of Civil Engineering and Mechanics,Lanzhou University,Lanzhou 730000,China)
†(AVIC Institute of Geotechnical Engineering Co.,Ltd.,Beijing 100098,China)
∗∗(College of Engineering,University of Arizona,Tucson,AZ 85721,USA)
As an important relation of the proportion in the history of mathematics,the golden section relation plays an important role in aesthetics,architecture,and even engineering.This paper studies the gold segmentation e ff ect for a class of vibration system of two degrees of freedom.The free vibration characteristics,and the resonance mechanism of the forced vibration under harmonic loading are analyzed.It is shown that,the ratios of the structure circular frequency to the layer sti ff ness and mass,and that of the structural amplitudes at two points conform well with the golden section ratio.The structure shows the beauty of harmony in vibration.
structural dynamics,golden section,two degrees of freedom,free vibration,forced vibration
O325
A
10.6052/1000-0879-16-306
2016–11–02收到第1稿,2016–12–14收到修改稿.
1)中央高校基本科研业务费专项资金(LZUJBKY-2016-110)和国家留学基金(201606185039)项目资助.
朱贝贝,孙兰宁,赵忠虎.一类二自由度系统振动的黄金分割率.力学与实践,2017,39(2):172-174 Zhu Beibei,Sun Lanning,Zhao Zhonghu.The golden section ratio of a class of vibration system of two degrees of freedom.Mechanics in Engineering,2017,39(2):172-174

