一种微操作平台的自适应运动跟踪控制

胡俊峰 郑昌虎 蔡建阳

江西理工大学机电工程学院，赣州，341000

一种微操作平台的自适应运动跟踪控制

胡俊峰 郑昌虎 蔡建阳

江西理工大学机电工程学院，赣州，341000

针对微操作平台的迟滞非线性和时变性，提出单神经元PID控制策略来对其进行运动跟踪控制，从而提高平台的运动精确性和响应快速性。采用RBF神经网络辨识器对微操作平台的梯度信息进行在线辨识，利用单神经元网络学习算法完成PID参数的在线自整定，实现微操作平台的自适应运动跟踪控制。为说明所提出控制方法的可行性，将其与普通PID控制方法进行了比较分析，实验结果表明，单神经元PID与普通PID控制的位移误差范围分别为-0.5～0.5μm、-2.5～2.5μm，调整时间分别为0.1s、0.4s，所提出控制方法具有更好的控制精度和响应快速性，并具有较强的自适应性。

微操作平台；单神经元PID控制；运动跟踪；RBF神经网络；压电驱动器

0 引言

目前，微操作平台在微细加工、微机电系统、生物工程、光学工程、医疗器械等领域的应用越来越广[1-3]。柔顺机构是利用柔性元件的弹性变形传递或转换运动和力的一种新型机构，具有无摩擦、无间隙、分辨率高和加工简单等优点，特别适宜作为微操作机器人机构。压电陶瓷(PZT)驱动器具有输出力大、响应快和刚度大等优点，将PZT驱动器与柔顺机构结合所组成的微操作平台具有操作精度高、动态性能好的优点。

但是，PZT存在迟滞现象以及蠕变与率相关等时变非线性特性，同时，加工误差会造成微操作平台结构参数的偏差，这些非线性和不确定因素均会降低平台的运动精度。为使微操作系统在运动跟踪过程中具有较高的响应速度和准确性，需要采用自适应和鲁棒性控制策略对其进行运动跟踪控制。

目前，提高微操作平台运动精度的控制方法主要为开环前馈控制与闭环反馈控制。开环前馈控制需要建立PZT的迟滞模型，利用其逆模型进行迟滞补偿，以便消除PZT迟滞现象对微操作平台的影响[4]，从而提高平台的运动精度。但是，建立平台迟滞模型过程复杂，且求解其逆模型困难，不能补偿微操作平台结构参数偏差产生的不确定性。目前，微操作平台进行运动跟踪控制的闭环控制方法主要为普通PID算法、模糊算法、遗传算法、滑模算法等[5-7]。闭环控制方法的适应能力强，可以对PZT驱动器与微操作平台的加工误差进行补偿。普通PID算法简单，易于实现，实用性强，但参数难整定；模糊算法[8]、遗传算法[9]、滑模算法[10]、神经网络算法[11-12]等智能控制方法自适应能力强，但算法复杂，难于实现实时在线控制。所以，需要寻找一种易于实现且具有自适应性的控制策略来实现微操作平台的运动跟踪。基于RBF神经网络的单神经元PID控制策略具有自适应和自学习能力，并且结构简单、易于实现，适用于具有高度非线性和不确定性的微操作平台的运动控制。

本文以某一维微操作平台为对象，针对微操作平台的迟滞非线性和时变性，提出一种基于RBF神经网络的单神经元PID控制策略来进行平台的运动跟踪控制。

1 微操作平台的模型

微操作平台由柔顺机构和PZT驱动器(呈电容特性[2])组成[1]，其等效模型如图1所示。图1中，C、R、Ka、Uin、Uout和x分别表示驱动器的等效电容、等效电阻、放大系数、输入电压、输出电压和输出位移。由Kirchhoff定理可得

(1)

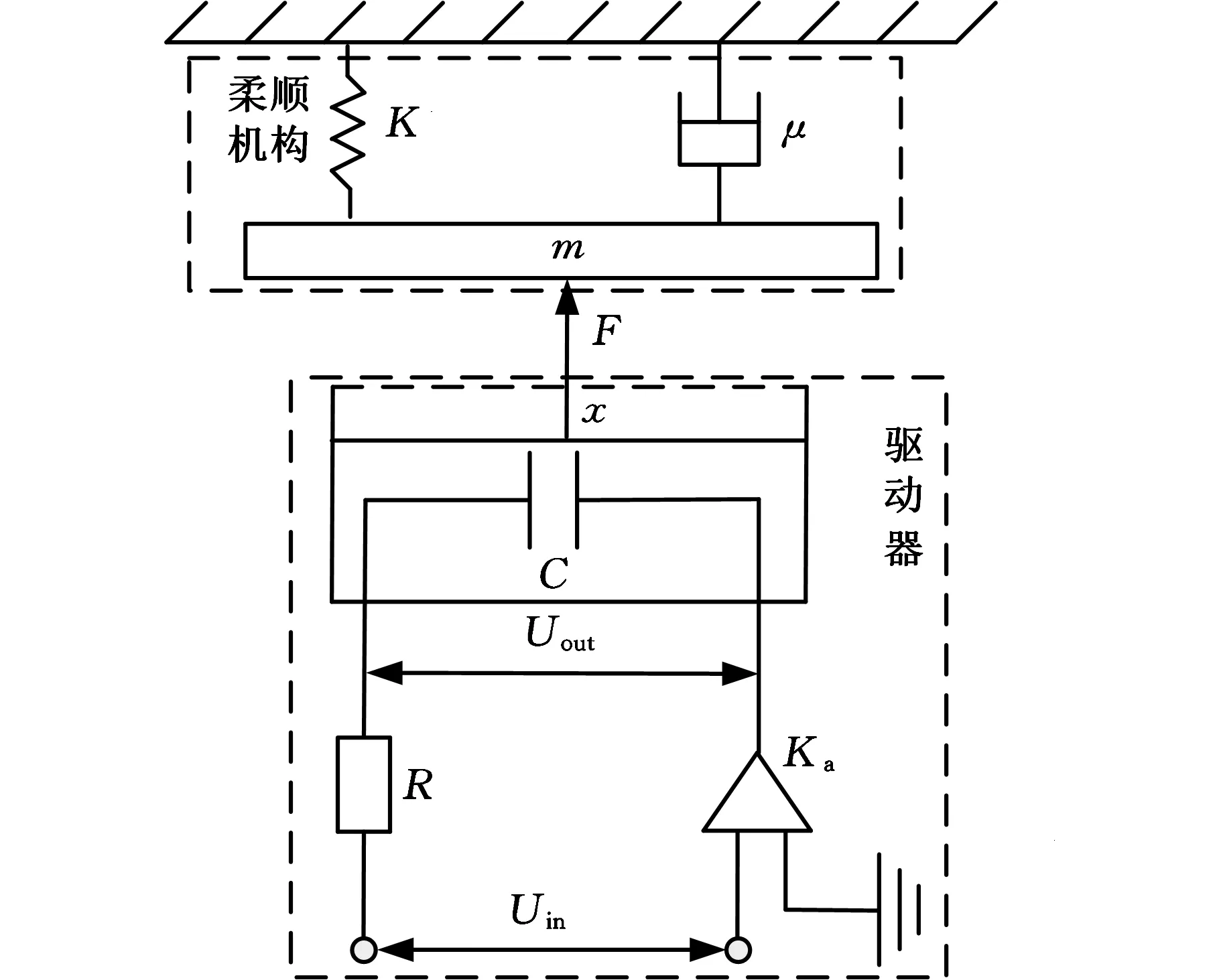
图1 微操作平台等效模型Fig.1 Equivalent model of micro-manipulation stage

由式(1)可得Uout到Uin的传递函数：

(2)

式中，T为时间常数，T=RC。

叠堆型压电驱动器由多片压电陶瓷片粘结而成，驱动器输出位移可表示为

x(t)=nd33Uin(t)

(3)

式中，n为压电陶瓷片个数；d33为应变系数。

联合式(2)、式(3)可得驱动器输出位移到输入电压之间的传递函数：

(4)

由式(4)可知，压电驱动器可等效为一阶惯性系统，但系统参数K1和T未知，为采用实验方法获取该参数，对驱动器施加阶跃信号Ua，其响应为

x(t)=K1(1-e-t/T)Ua

(5)

式(5)中的K1和T可通过阶跃响应实验测得。t=4T时，一阶系统的响应已达稳态值的98%，可认为PZT达到稳态。设系统达到稳态所需时间为ts，稳态输出位移为x(ts)，则可得参数：

(6)

柔顺机构可简化为质量-弹簧-阻尼系统，如图1所示。图1中，m为柔顺机构的质量，μ为机构的阻尼系数，K为机构刚度，F为压电驱动器输出力，y为平台的输出位移。压电陶瓷为有限刚度的弹性器件，故驱动器作用在柔顺机构的输出力为

F=Ktx

(7)

式中，Kt为压电驱动器的刚度。

则柔顺机构的动力学方程可表示为

(8)

对式(8)进行拉氏变换并化为标准形式

(9)

式中，ωn为柔顺机构的无阻尼固有频率；K2为放大系数；ξ为阻尼比。

由式(9)可知，要确定柔顺机构的模型，需要先确定参数K2、ωn和ξ。ωn和ξ可采用实验模态测试方法得到。

由图1可知，微操作系统是驱动器与柔顺机构组成的串联系统，联合式(4)、式(9)可得其传递函数：

(10)

对PZT驱动器施加阶跃电压Ua，由终值定理可得平台响应的稳态值：

(11)

由式(11)可得

K2=y(∞)/(K1Ua)

(12)

由式(12)可知，只要确定平台阶跃响应的稳态值就可确定参数K2。

2 基于RBF神经网络的单神经元PID控制

单神经元PID控制器结构如图2所示，其中，r(k)、y(k)分别为采样时刻t=kTs(Ts为采样周期)时微操作平台的期望位移和实际输出位移，Uout(k)为控制器的输出电压，kP为比例系数，wi(i=1，2，3)为连接权值，z-1表示延迟环节。r(k)与y(k)经状态转换得到单神经元的输入：

(13)

式中，e(k)为微操作平台的目标位移与实际位移的偏差，e(k)=r(k)-y(k)。

单神经元PID控制器的输出为

(14)

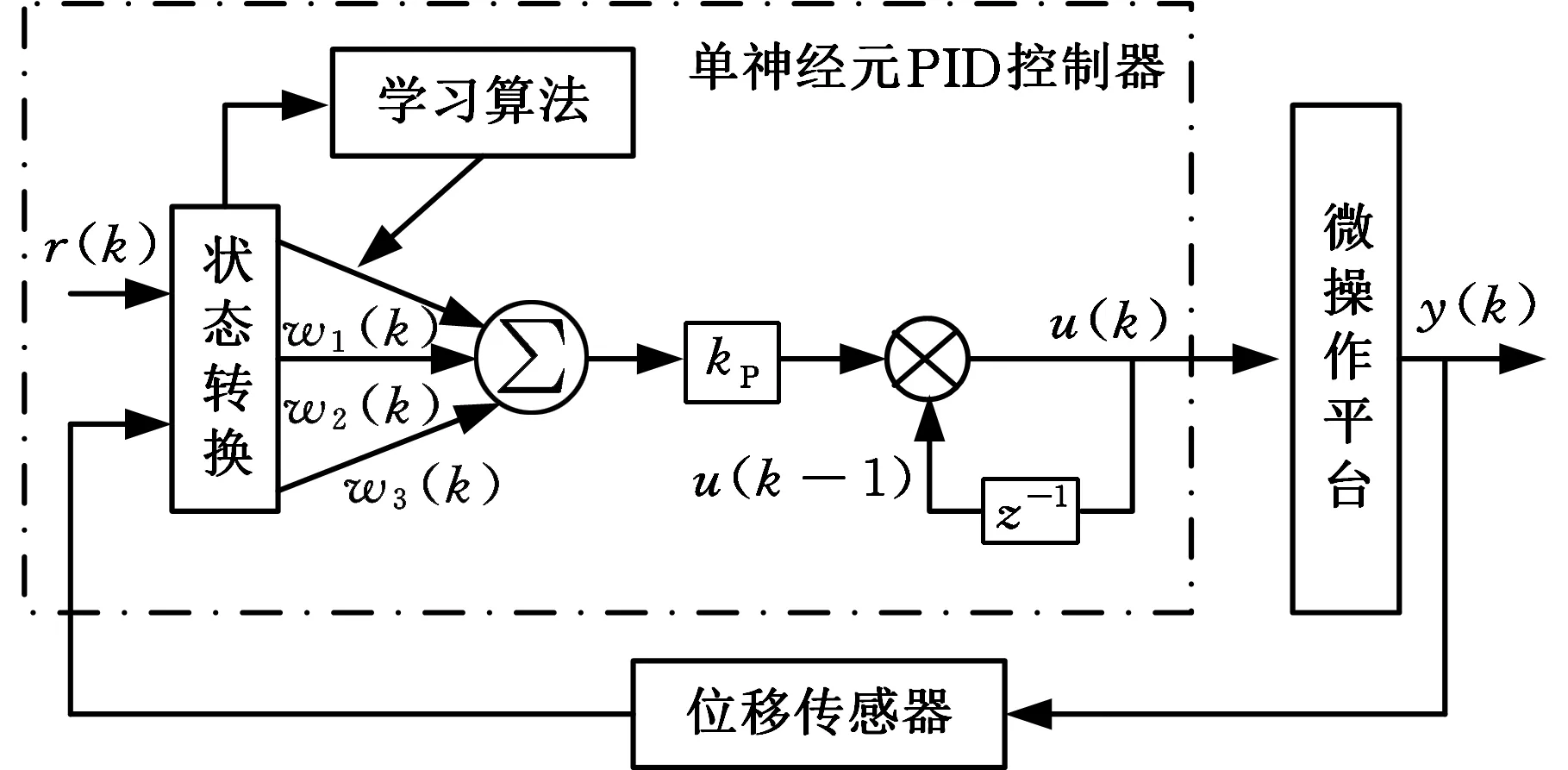
图2 单神经元PID控制器结构Fig.2 Structure of single neuron PID controller

普通增量式PID控制器输出可表示为[14]

Uout(k)=Uout(k-1)+kPx1+kIx2+kDx3

(15)

对比式(14)、式(15)可知，单神经元PID的连接权值w1、w2与w3相当于增量式PID的比例系数kP、积分系数kI与微分系数kD。单神经元PID与普通PID不同之处在于，可通过有监督的Hebb学习规则在线实时自调整连接权值wi，以实现微操作平台的自适应和自学习控制。为了实现连接权值的自适应调整，引入最优控制的二次型性能指标：

E=(r(k+1)-y(k+1))2/2

(16)

为求取E的最小值，采用梯度下降法对式(16)进行调整，得到wi的迭代表达式

(17)

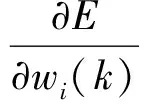
(18)

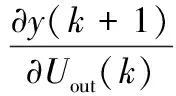
联合式(17)、式(18)可得连接权值wi的修正值：

Δwi=wi(k+1)-wi(k)=

(19)

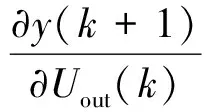
基于RBF神经网络的单神经元PID控制系统结构如图3所示，图中，yout(k+1)可以通过RBF神经网络辨识逼近微操作平台的实际输出位移y(k+1)，则平台梯度信息为

(20)

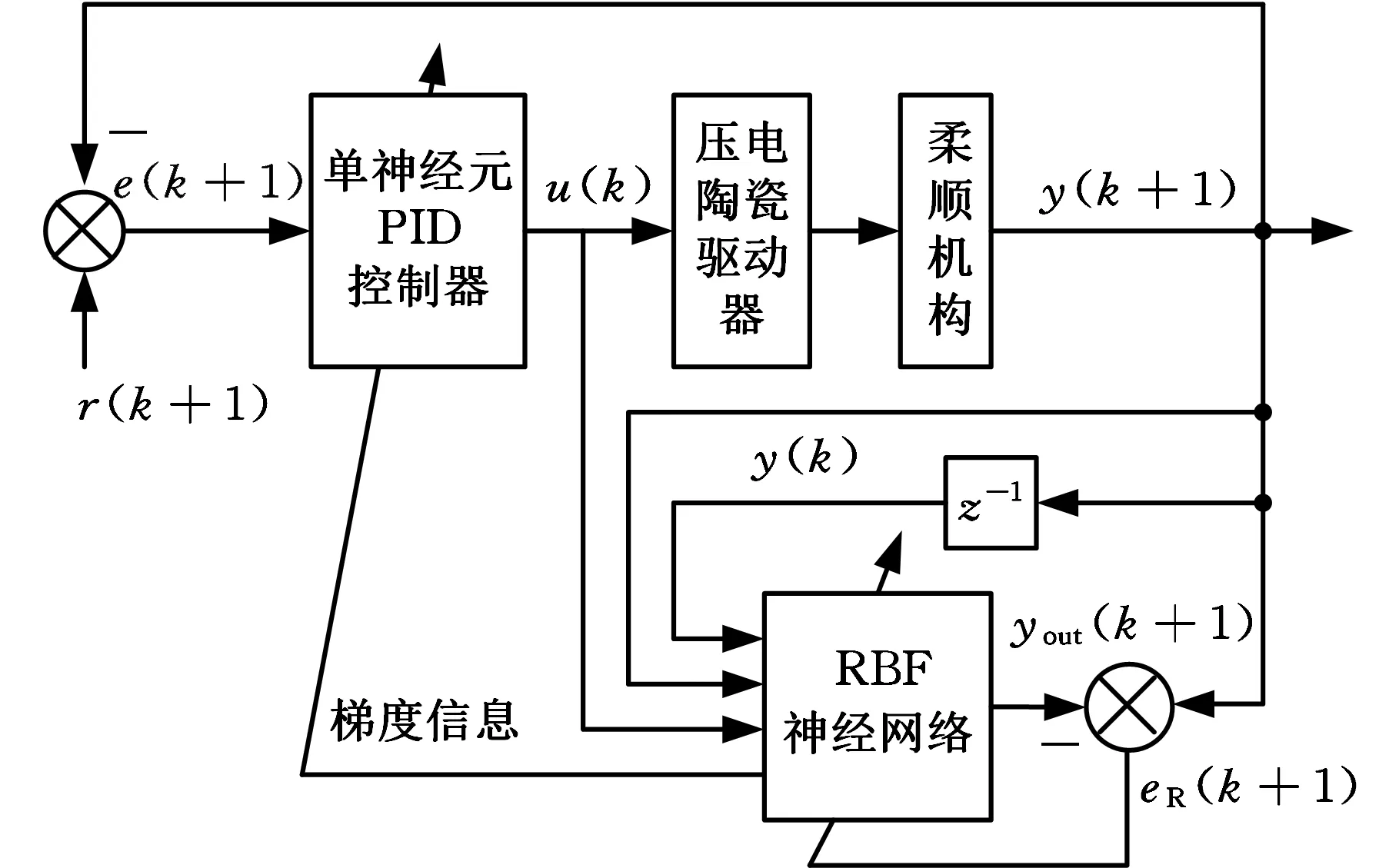
图3 基于RBF神经网络的单神经元PID控制系统Fig.3 Single neuron PID control system based on RBF neural network

联合式(19)、式(20)可得单神经元PID连接权值的修正值

(21)

(22)

隐层具有6个神经元，隐层径向基函数为高斯核函数，第j(j=1，2，…，6)个隐层单元的输出为

(23)

X=(xR1，xR2，xR3)Cj=(cj1，cj2，cj3)

其中，Cj为第j个隐层神经元的中心点矢量；|X-Cj|为X与Cj之间的距离，Cj越接近输入值，高斯函数对输入越敏感；bj为高斯函数的宽度，影响高斯函数对输入的映射能力。

RBF网络隐层到输出层的映射是线性的，网络输出为

(24)

式中，wcj为连接隐层第j个神经元与对应输出层的权值。

由式(23)、式(24)可知，RBF神经网络的未知参数包括基函数的中心向量Cj、宽度bj和输出层的连接权值wcj。为此，设定辨识系统的学习目标

J=(y(k+1)-yout(k+1))2/2

(25)

为了实现最佳逼近，采用梯度下降法分别沿J对cji、bj、wcj的负梯度方向搜索可得RBF神经网络的未知参数[13]

(26)

eR(k+1)=y(k+1)-yout(k+1)式中，ηR为RBF神经网络的学习速率，取值范围为[0，1]。

所以，联合式(22)～式(24)可得平台梯度信息：

(27)

根据上述理论可归纳出基于RBF网络在线辨识的单神经元PID自适应控制算法流程，如图4所示。

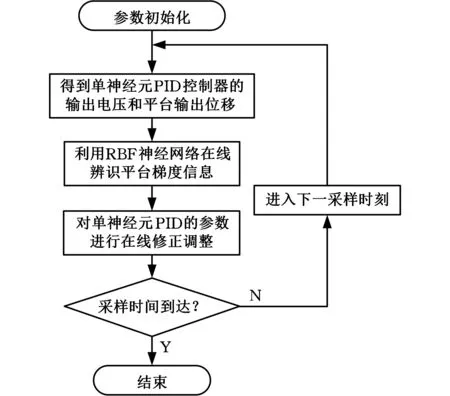
图4 控制算法流程Fig.4 Processes of control algorithm

(1)初始化单神经元权值wi、学习速率η，RBF神经网络参数Ci、bi、wci和学习速率ηR，确定采样周期Ts与采样时间，设定所期望的平台运动位移信号。

(2)采样得到t=kTs时刻的期望位移r(k)与实际输出位移y(k)，由式(13)可计算得到该时刻单神经元的输入xi，由式(14)计算得单神经元PID控制器的输出Uout(k)。Uout(k)作用于微操作平台时，平台会产生下一步的实际输出位移，即时刻t=(k+1)Ts的实际输出位移y(k+1)。

(3)将Uout(k)、y(k+1)与y(k)输入RBF神经网络，由式(24)可计算得RBF网络的辨识输出yout(k+1)。

(4)根据y(k+1)与yout(k+1)产生的偏差信息，由式(26)对RBF网络的各参数进行修正。

(5)根据修正后的RBF网络，由式(27)可求得平台的梯度信息∂yout(k+1)/∂Uout(k)。

(6)根据平台的期望与实际输出位移之间的偏差e(k+1)和梯度信息∂yout(k+1)/∂Uout(k)，由式(21)对单神经元的权值wi进行在线修正。

(7)判断采样时间是否到达，若已到达，则停止，若未到达，则令k←k+1，返回步骤(2)继续执行。

根据上述的控制算法可知，该算法采用RBF神经网络对微操作平台进行在线辨识，利用辨识的输出获得平台的梯度信息，并利用该梯度信息对单神经元PID的权值进行在线实时调整，实现了在线学习和自适应控制，可消除微操作平台的迟滞现象和系统的不确定性。

3 试验验证

如图5所示，试验装置由柔顺机构、PZT驱动器、驱动电源、位移传感器、信号调理器、D/A卡、工控机组成。压电驱动器为哈尔滨芯明天公司生产的80VS12，驱动电源为芯明天公司的XE-501，位移传感器为PI 公司生产的D-E20.200，D/A卡和A/D卡分别为NI公司的PCI-6713和PCIe-6341。首先，通过实验方法确定式(10)中传递函数的参数T、K1、K2。实验数据采集过程如图6所示，采用LabVIEW软件产生一阶跃信号，信号电压Ua(Ua=4 V)经功率放大后，作为压电驱动器的输入电压Uin(Uin=60 V)，采用位移传感器测量出驱动器的输出位移x与微操作平台的输出位移y。

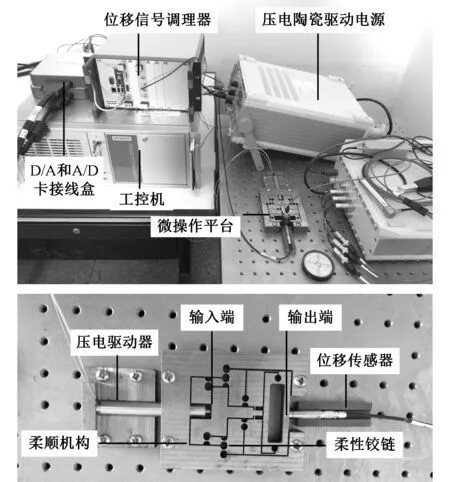
图5 实验配置Fig.5 Experiment setup

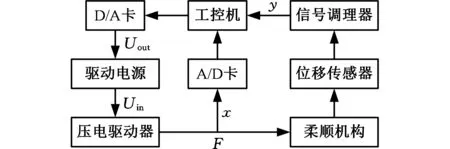
图6 实验数据采集过程Fig.6 Acquisition process of experimental data

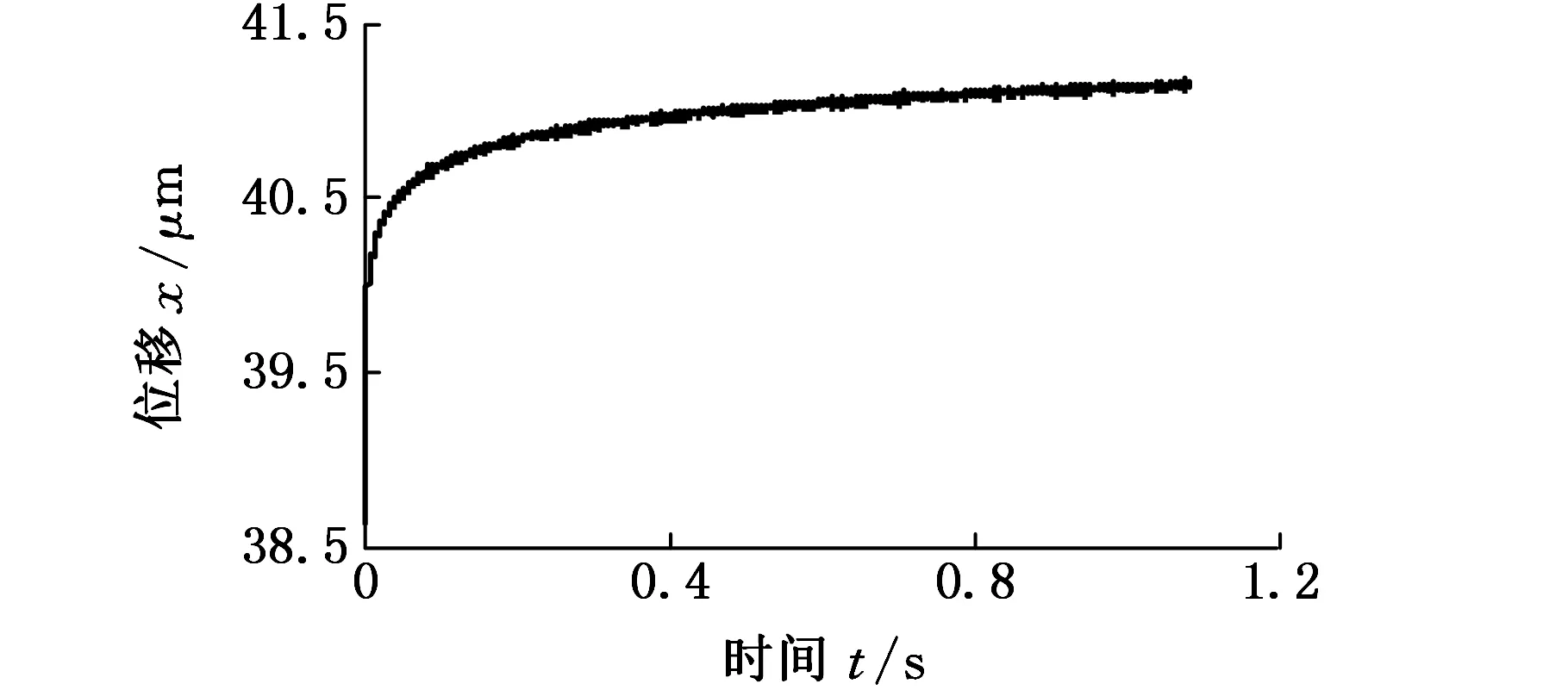
图7 压电陶瓷驱动器阶跃响应Fig.7 Step response of piezoelectric actuator

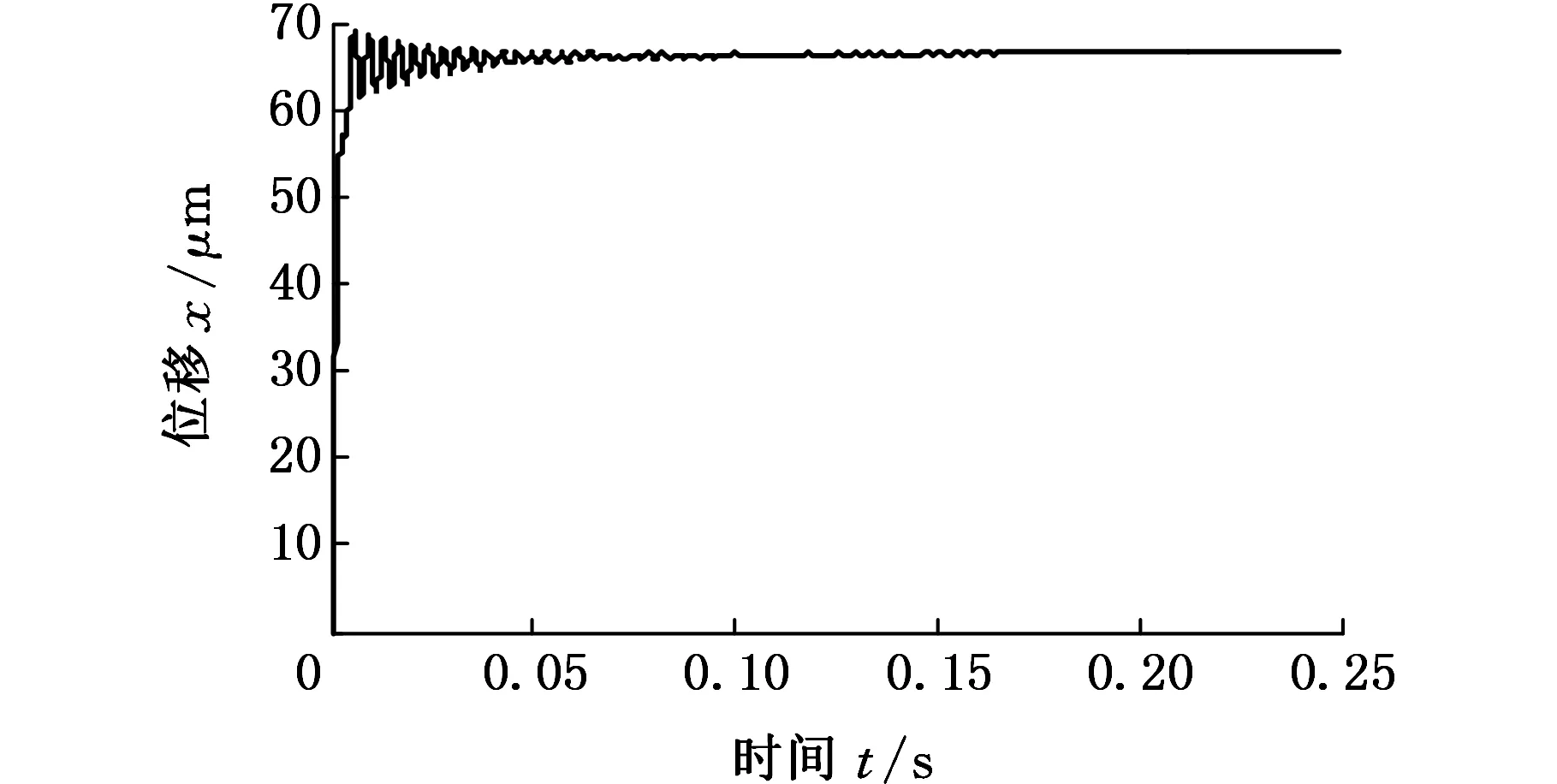
图8 微操作平台阶跃响应Fig.8 Step response of micro-manipulation stage

压电驱动器和平台的输出位移分别如图7、图8所示。由图7可知，压电驱动器为一阶系统，其响应稳定值为41.3 μm，由式(6)可得参数T=0.01 s，K1=10.325。由图8可知，平台的阶跃响应稳态值为67 μm，由式(12)可得参数K2=1.622。

微操作平台的阻尼系数可以通过实验模态[14]测试得到。如图9所示，实验模态测试的实验装置包括力锤、加速度传感器、动态信号分析仪。加速度传感器为PCB公司的Model 356A16。采用脉冲锤击法进行实验模态测试，用力锤在平台不同位置进行敲击，产生一个宽频带的激励，敲击点为图9中的A、B、C、D。加速度传感器位于微操作平台的输出端，测量4个不同敲击点的加速度信号。为消除噪声干扰，对每个敲击点进行多次测量，每个测点的测量次数为5。使用激励点和各测量点的时间历程数据，利用软件DHDAS求出各测点的频响函数曲线，如图10所示。采用导纳圆法对4组频响数据进行曲线拟合，得到系统的固有频率ωn=231 Hz，阻尼比ξ=0.159。

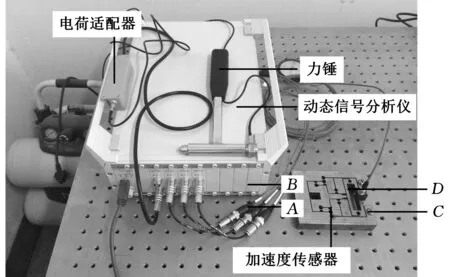
图9 模态实验配置Fig.9 Modal experiment setup

图10 实验模态的频响曲线Fig.10 Frequency response curve of experiment modal

将参数ωn、ξ、T、K1和K2代入式(10)，可得微操作平台的传递函数：

(28)

为了验证所提出控制算法的有效性和优越性，将其与普通PID控制进行了对比分析。由式(28)所示的微操作平台动力学模型，采用ZN临界比例法[15]进行整定可得PID参数kP=0.84，kI=67.2，kD=1.2。单神经元PID连接权值相当于普通PID的比例系数、积分系数与微分系数，单神经元PID连接权值的初始值分别设为kP、kI、kD，学习速率η=0.2，kP=0.9。RBF神经网络的连接权值wcj的初始值为0、1之间的随机数，学习速率ηR=0.2。中心向量Cj离RBF网络输入量越近，高斯函数对输入越敏感，因此可根据RBF网络的输入值范围确定Cj，考虑到实际的xR1为D/A采集卡输出电压，其范围为0～10 V，xR2与xR3为平台输出位移，设定目标位移最大值为20 μm，xR2与xR3的范围为0～20 μm，则取高斯核函数参数C的初始值：

(29)

设hj=0.5，将Cj与X的初始值代入式(23)求得bj的初始值100。设采样周期Ts=5 ms，采样时间为2 s。

图11 跟踪正弦信号时的输出位移Fig.11 Output displacements when tracking a sinusoidal signal

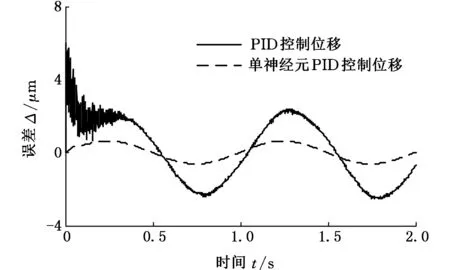
图12 跟踪正弦信号时的输出位移误差Fig.12 Output displacement error when tracking a sinusoidal signal

为说明所设计的控制算法在平台运动跟踪过程中具有较高的精确性和快速性，首先设微操作平台的期望位移为正弦信号r(t)=10 sin(2πt-π/2)+10，如图11所示，该期望位移要求平台输出端的运动行程为0～20 μm，频率为1 Hz。分别采用基于RBF神经网络的单神经元PID算法与普通PID算法进行运动跟踪控制，由2种控制算法得到平台的实际输出位移如图11所示，它们与期望位移的误差如图12所示。由图11、图12可知，采用普通PID控制算法进行运动跟踪控制时，运动初始阶段的跟踪误差较大，不能即时跟踪到目标位移，0.4 s后能跟踪到所期望位移，但运动误差范围为-2.5～2.5 μm；采用所提出算法进行运动跟踪控制时，在初始阶段就能跟踪到期望位移，且运动误差范围为-0.5～0.5 μm。所以，与普通PID控制相比，单神经元PID控制的运动跟踪更快、更准确。

单神经元PID的连接权值调整情况如图13所示，由图13可知，连接权值在运动跟踪过程中是随时间变化的，即控制器可以根据微操作平台的实际情况进行PID参数的实时调整，实现自适应控制；在运动跟踪初始阶段，w1和w2会发生较小的变化，w3迅速增大。由图11可知，普通PID算法在初始阶段产生较大的误差，单神经元PID通过增大w1、w2，使跟踪误差减小；误差减小后，减小w1、w2至合适值并保持稳定，增大w3，提高微操作平台的响应快速性，使其能更快地进行位移跟踪。所以，相比于普通PID控制，单神经元PID可以自动调整参数，迅速减小误差，使其能更快地进行位移跟踪。

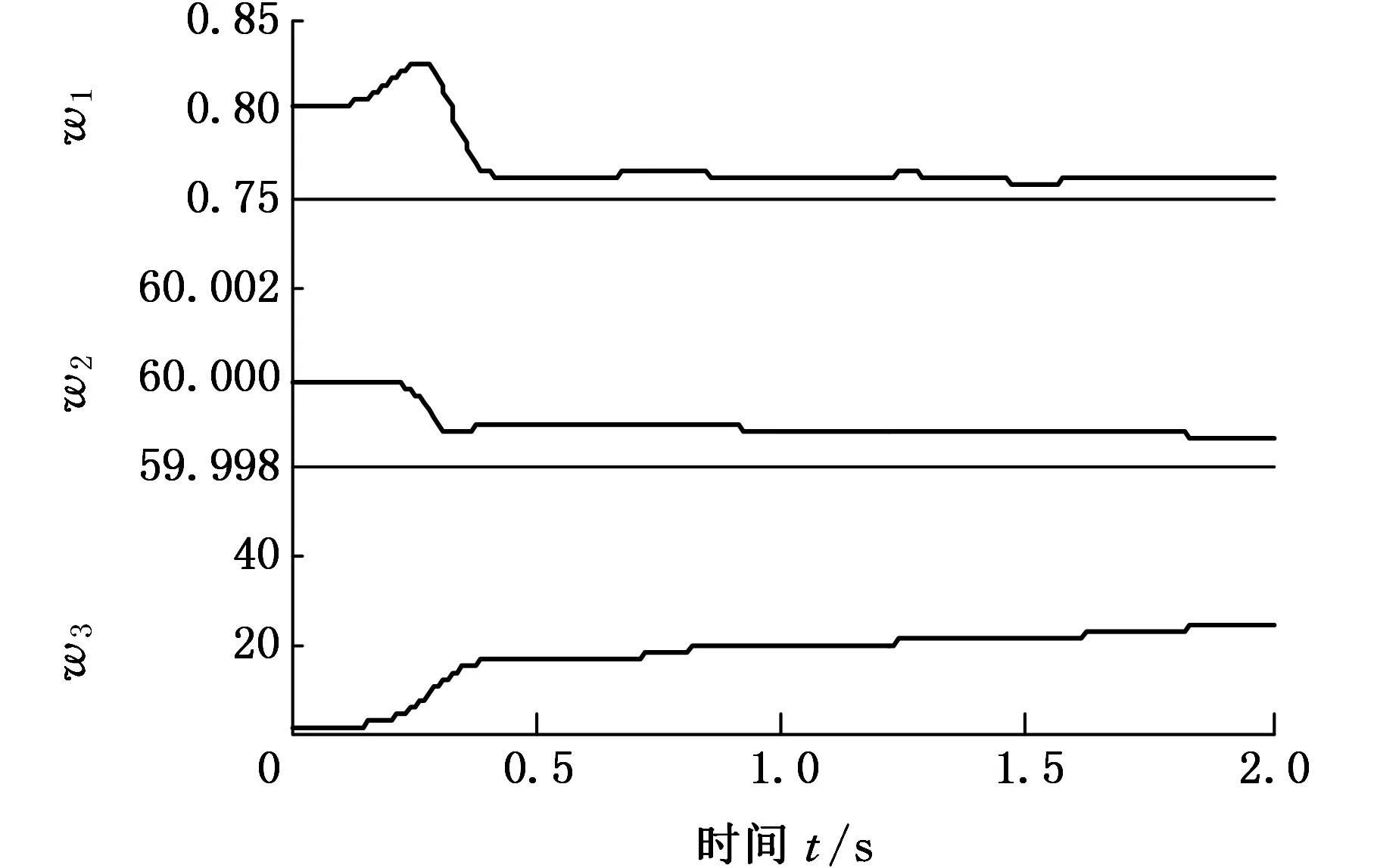
图13 跟踪正弦信号时连接权值调整情况Fig.13 Connection weight adjustment when tracking sinusoidal signal

为进一步说明所提出控制策略的运动跟踪响应快速性，设微操作平台所跟踪的期望位移为图14所示的方波信号(该期望位移要求平台输出端的运动行程为0～20 μm，频率为1 Hz)，分别采用所提出算法与普通PID算法进行运动跟踪控制，得到平台的实际输出位移，如图14所示。由图14可知，文中算法的调整时间约为0.1 s，PID算法的调整时间约为0.4 s，说明所提出的算法具有更快的响应速度。

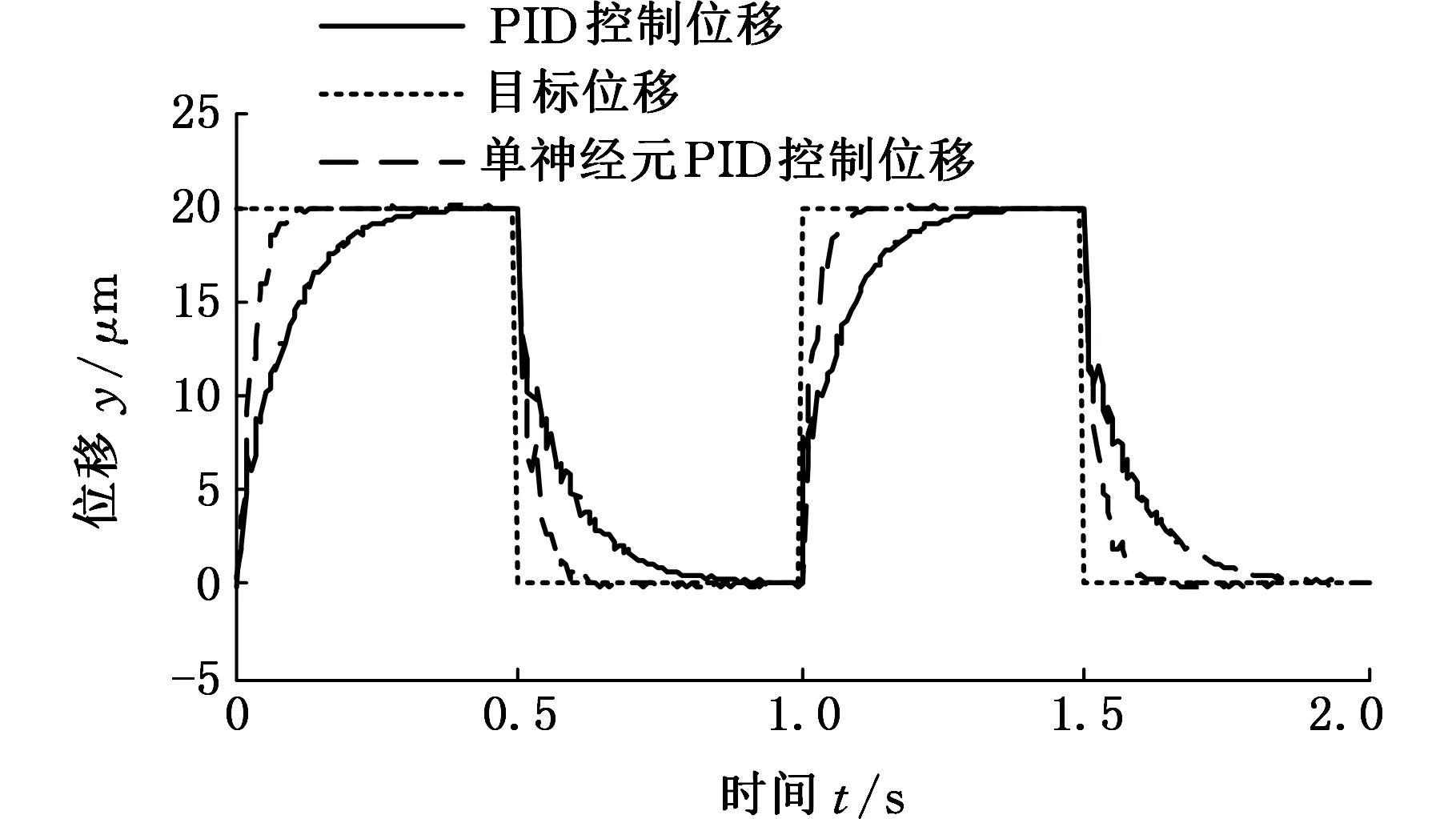
图14 跟踪方波信号时的输出位移Fig.14 Output displacements when tracking a square signal

方波信号在转折处的变化快，要求平台在跟踪方波信号时具有较高的响应速度，单神经元PID能通过改变连接权值实现平台的快速响应。PID连接权值的变化情况如图15所示，由图15可知，在方波信号的转折点处，w1、w2产生较小的波动，w3会迅速增大，参数的这种变化会缩短平台的调整时间，从而提高平台的运动跟踪响应速度。所以，所提出的控制方法能根据微操作平台的实际情况进行自适应控制，消除平台的迟滞非线性和不确定性对平台运动精度和响应性的影响。

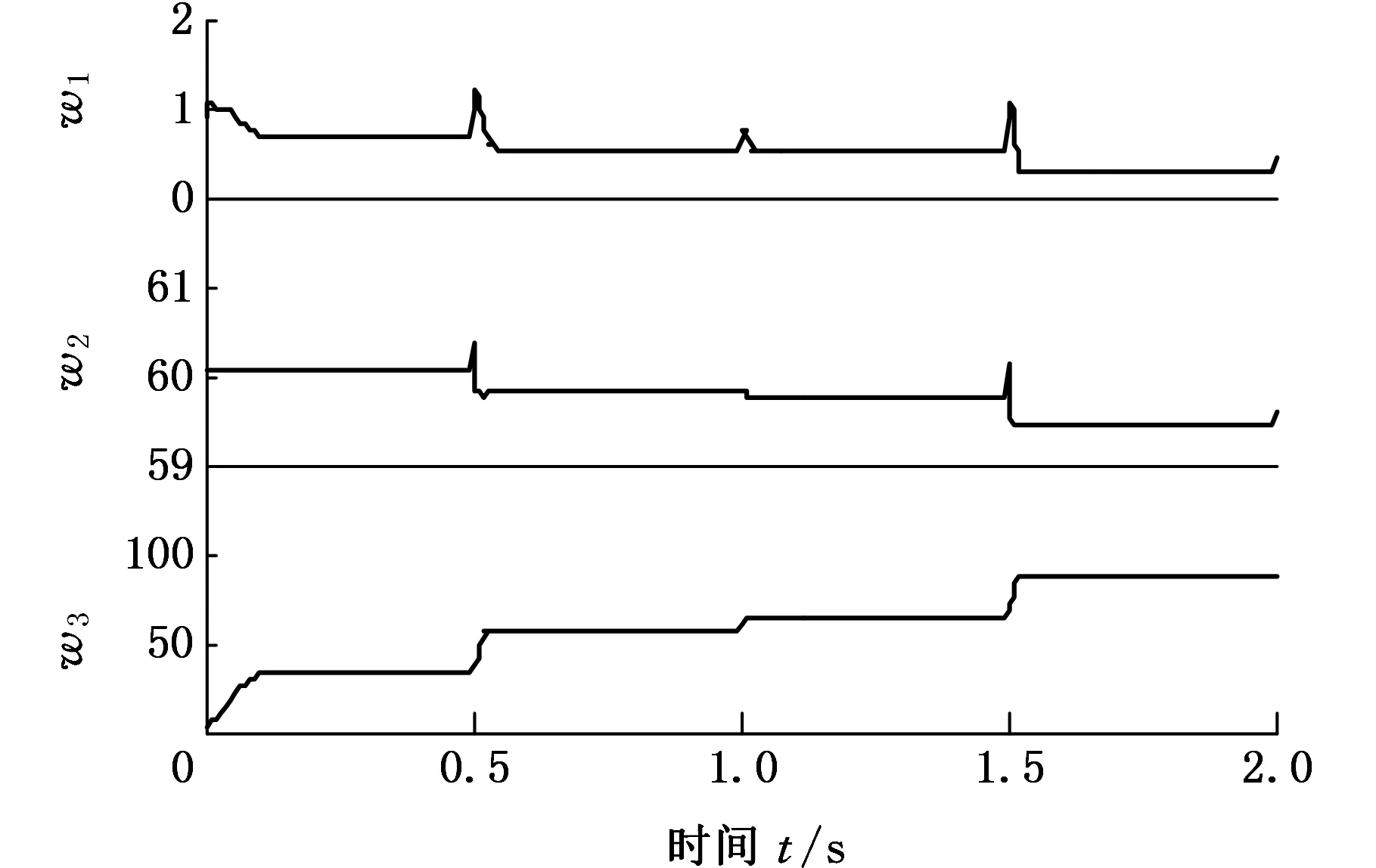
图15 跟踪方波信号时连接权值调整情况Fig.15 Connection weights adjustment when tracking a square signal

4 结语

针对微操作平台的迟滞与时变特性，提出一种基于RBF神经网络的单神经元PID控制策略来对其进行运动跟踪控制。采用实验方法建立了微操作平台的传递函数，基于该传递函数可得单神经元PID控制参数的初始值，利用RBF神经网络在线辨识建立了微操作平台模型。该模型为单神经元PID控制器提供梯度信息，从而实现PID控制器参数的在线自整定，进而实现微操作平台的自适应控制。为说明所提出控制算法的可行性，将其与普通PID控制算法进行了比较分析。对比结果表明，基于RBF的单神经元PID控制的跟踪误差更小、跟踪速度更高，说明所提出控制方法的控制精度高、动态特性好。

[1] 胡俊峰, 徐贵阳, 郝亚洲. 基于响应面法的微操作平台多目标优化[J]. 光学精密工程, 2015, 23(4):1096-1104.HUJunfeng,XUGuiyang,HAOYanzhou.Multi-objectiveOptimizationofaNovelMicro-manipulationStageBasedonResponseSurfaceMethod[J].OpticsandPrecisionEngineering, 2015, 23(4):1096-1104.

[2] 胡俊峰, 郝亚洲, 徐贵阳, 等. 一种新型微操作平台的精确运动控制[J]. 机械科学与技术, 2016, 35(2):216-221.HUJunfeng,HAOYanzhou,XUGuiyang,etal.PrecisionMotionControlofaNovelMicro-manipulationStage[J].MechanicalScienceandTechnologyforAerospaceEngineering, 2016, 35(2):216-221.

[3]LIAWHC,SHIRINZADEHB.ConstrainedMotionTrackingControlofPiezo-actuatedFlexure-basedFour-barMechanismsforMicro/NanoManipulation[J].IEEETransactionsonAutomationScience&Engineering, 2010, 7(3):699-705.

[4]LINCJ,LINPT.TrackingControlofaBiaxialPiezo-actuatedPositioningStageUsingGeneralizedDuhemModel[J].Computers&MathematicswithApplications, 2012, 64(5):766-787.

[5]JIANGH,JIH,QIUJ,etal.AModifiedPrandtl-ishlinskiiModelforModelingAsymmetricHysteresisofPiezoelectricActuators[J].IEEETransactionsonUltrasonicsFerroelectrics&FrequencyControl, 2010, 57(5):1200-1210.

[6]XIAOShunli,LIYangmin.ModelingandHighDynamicCompensatingtheRate-dependentHysteresisofPiezoelectricActuatorsviaaNovelModifiedInversePreisachModel[J].IEEETransactionsonControlSystemsTechnology, 2013, 21(5):1549-1557.

[7]ZUBIRMNM,SHIRINZADEHB,TIANY.DevelopmentofNovelFlexure-basedMicrogrippersforPrecisionMicro-objectManipulation[J].SensorsandActuatorsA:Physical, 2009, 150(2):257-266.

[8] 张建华, 葛红宇, 李宏胜, 等. 压电致动器Preisach模型的模糊插值算法及实现[J]. 南京理工大学学报, 2011, 35(6):780-785.

ZHANGJianhua,GEHongyu,LIHongsheng,etal.FuzzyInterpolationAlgorithmandRealizationofPreisachModelforPiezoActuator[J].JournalofNanjingUniversityofScienceandTechnology, 2011, 35(6):780-785.

[9]BIGLARM,GROMADAM,STACHOWICZF,etal.OptimalConfigurationofPiezoelectricSensorsandActuatorsforActiveVibrationControlofaPlateUsingaGeneticAlgorithm[J].ActaMechanica, 2015, 226(10):1-12.

[10]KORAYEMMH,NOROOZIM,DAEINABIK.ControlofanAtomicForceMicroscopyProbeduringNano-manipulationviatheSlidingModeMethod[J].ScientiaIranica, 2012, 19(5):1346-1353.

[11]MOHAMMADRZ,MOHSENF,HASSANS.etal.HysteresisNonlinearityIdentificationUsingNewPreisachModelBasedArtificialNeuralNetworkApproach[J].JournalofAppliedMathematics, 2011(22):1-21.

[12]SHINJM,YANGSH,HANSI.SlidingModeRecurrentWaveletNeuralNetworkControlforRobustPositioningofUncertainDynamicSystems[J].ProceedingsoftheInstitutionofMechanicalEngineersPartI：JournalofSystems&ControlEngineering, 2010, 224:932-946.

[13] 刘金琨.RBF神经网络自适应控制MATLAB仿真 [M]. 北京:清华大学出版社, 2014.LIUJinkun.MATLABSimulationonRBFNeuralNetworkAdaptiveControl[M].Beijing:TsinghuaUniversityPress, 2014.

[14] 徐飞, 李传日, 姜同敏, 等. 模态试验激励点与响应点优化分析[J]. 北京航空航天大学学报, 2013, 39(12):1654-1659.XUFei,LIChuanri,JIANGTongmin,etal.OptimizationofExcitationandMeasurementLocationinExperimentalModalTest[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013, 39(12):1654-1659.

[15] 刘玲玲.PID参数整定技术的研究及应用 [D]. 郑州:郑州大学, 2010.LIULinlin.ResearchandApplicationonthePIDParametersTuningTechnology[D].Zhengzhou:ZhengzhouUniversity, 2010.

(编辑 张 洋)

Adaptive Motion Tracking Control of a Micro-manipulation Stage

HU Junfeng ZHENG Changhu CAI Jianyang

School of Mechanical & Electrical Engineering,Jiangxi University of Science and Technology, Ganzhou,Jiangxi,341000

Considering hysteresis nonlinearity and time variation of micro-manipulation stage, a single neuron PID control strategy was proposed for motion tracking control to improve motion accuracy and response of the stage. Gradient informations of the micro-manipulation stage might be obtained online by RBF neural network identifier, and learning algorithm of single neuron network was applied to achieve online self-tuning of PID parameters to achieve the adaptive motion tracking control of the micro-manipulation stage. In order to illustrate the feasibility of the proposed control method, experimental comparative analyses with ordinary PID control were carried out. Experimental results show that, displacement error ranges of the single neuron PID are as -0.5～0.5 μm, and the adjustment time of that is as 0.1 s, while displacement error ranges of ordinary PID control are as -2.5～2.5 μm, and the adjustment time of that is as 0.4 s. It shows that the proposed control method has better control accuracy, response speed, and stronger adaptability.

micro-manipulation stage; single neuron PID control; motion tracking; radial basis function(RBF) neural network; piezoelectric actuator

李 凡，男，1992年生。河北工业大学机械工程学院硕士研究生。主要研究方向为移动机器人。发表论文1篇。张明路，男，1946年生。河北工业大学机械工程学院教授、博士研究生导师。吕晓玲(通信作者)，女，1981年生。河北工业大学机械工程学院讲师。E-mail:lxl000418@163.com。田 颖，女，1987年生。河北工业大学机械工程学院讲师。白 丰，男1988年生，河北工业大学机械工程学院博士研究生。

2016-06-07

国家自然科学基金资助项目(51265016,51565016)

TH703;TP274

10.3969/j.issn.1004-132X.2017.08.005