介观尺度磷青铜薄板韧性断裂和变形行为的尺寸效应

王 蕾 胡道春

1.台州学院机械工程学院，台州，3180002.台州职业技术学院机电工程学院，台州，318000

介观尺度磷青铜薄板韧性断裂和变形行为的尺寸效应

王 蕾1胡道春2

1.台州学院机械工程学院，台州，3180002.台州职业技术学院机电工程学院，台州，318000

借助单轴微拉伸试验研究了磷青铜薄板力学性能和韧性断裂的尺寸效应。结果表明，屈服强度与材料厚度t、晶粒尺寸d之间均存在着第Ⅱ类尺寸效应，但与t/d之间却存在着第Ⅰ类尺寸效应。断口形貌显示，随着t的减小，断裂机制由韧窝-微孔聚集断裂向滑移分离过渡；随着d的增大，韧窝逐渐变大变深，但当t/d<1时，拉伸过程过早形成微裂纹，导致试样迅速断裂。最后，基于表面层模型构建了介观尺度磷青铜薄板的混合本构方程。

磷青铜; 断口分析；屈服强度; 尺寸效应

0 引言

功能集成化和体积微小化所带来的产品微型化已成为工业界不可阻挡的趋势，同时也导致零件的微细化并推动微细制造技术的发展。微型化产品零件的几何特征尺寸一般为0.01～1 mm，且其相对精度定义在10-1～10-2mm/mm，属于介观尺度[1-3]。介观尺度零件的成形加工技术即介观成形(meso forming)，受到了国内外专家学者的广泛关注，大量的研究也在介观成形领域展开。

介观成形也称为微成形、微塑成形、微细成形，其典型工艺包含介观冲压、介观挤压、介观压印、介观模锻等[4]。与传统塑性成形工艺相比，介观成形机理和材料流动规律发生了一定的变化。VOLLERTSEN等[5]根据尺寸效应产生的物理来源和结构来源，指出尺寸效应主要分为特征尺寸效应(feature size effects)、材料本身的晶粒尺寸效应(grain size effects)。

单轴拉伸试验作为一种简单且便于测量材料力学性能的方法，被国内外众多学者用于研究介观尺度薄板材料力学性能的尺寸效应。HOFFMANN等[6]通过拉伸试验研究了不同厚度薄板流动应力的尺寸效应，发现在25～500 μm厚度范围内的流动应力表现出“越小越弱”的尺寸效应，文献[7-8]将这类“越小越弱”的尺寸效应称为第Ⅰ类尺寸效应，并在晶体塑性变形物理机制的基础上利用表面层模型对这种现象进行了理论分析。但KALS等[9]、RAULEA等[10]通过单轴拉伸试验发现，流动应力并非一直随着板料几何尺寸的减小而减小，他们在试验中同时考虑板料厚度和晶粒尺寸的影响，采用量纲一的比例因子(厚度t与晶粒尺寸d的比值)λ=t/d来表征薄板力学性能的尺寸效应。结果表明，λ>1时，屈服强度随着板厚方向晶粒的减少而降低；λ<1时，却随着晶粒尺寸的增大而升高，这类“越小越强”的尺寸效应称之为第Ⅱ类尺寸效应。GEIGER等[11]、PERNIN等[12]引入材料内禀尺寸，通过视塑性法、应变梯度理论从晶粒取向选择性、位错滑移的角度分别对该现象进行了合理的解释。

磷青铜具有良好的力学性能、耐腐蚀抗磨损、冲击时不易产生火花等优点，常应用于航空宇航、电机电器、电子信息等行业领域的耐磨零件和弹性元件[13]。随着“轻、薄、短、小”等介观尺度特征零件的产业化需求，开展磷青铜薄板微成形过程中的力学性能和韧性断裂的尺寸效应研究很有必要。

1 磷青铜薄板单轴拉伸试验

1.1 试样制备

1.1.1 试验材料

试验所用材料为C5191-H磷青铜(对应国内牌号为QSn6.5-0.1)，其质量分数如下：Sn为5.5%～7.0%，P为0.11%～0.13%，Fe为 ≤ 0.02%，Pb为≤0.05%，Zn为≤0.20%，其余为Cu。

1.1.2 试样制备

为获得不同晶粒尺寸的磷青铜薄板，将厚度t为50 μm、100 μm、250 μm的薄板放到热处理炉中分别进行300 ℃、400 ℃、500 ℃、600 ℃和700 ℃的退火试验。参照有色金属行业标准YS/T449-2002，对退火热处理后的薄板试样进行冷镶、抛光、腐蚀、金相观测和晶粒尺寸测量，获得的晶粒尺寸如表1所示。

表1 磷青铜薄板退火后的晶粒尺寸

根据相似性原则，将宏观拉伸试样等比缩放为薄板拉伸试样，在试样两端设计工艺孔以配合夹具夹持，并减少夹持端的夹持力不稳定对试验误差的影响。另外，在试样多片组合慢走丝线切割时采用“割三修四”的特殊工艺，以保证试样标距段的精度，减小氧化层的不利影响。拉伸试样如图1所示。

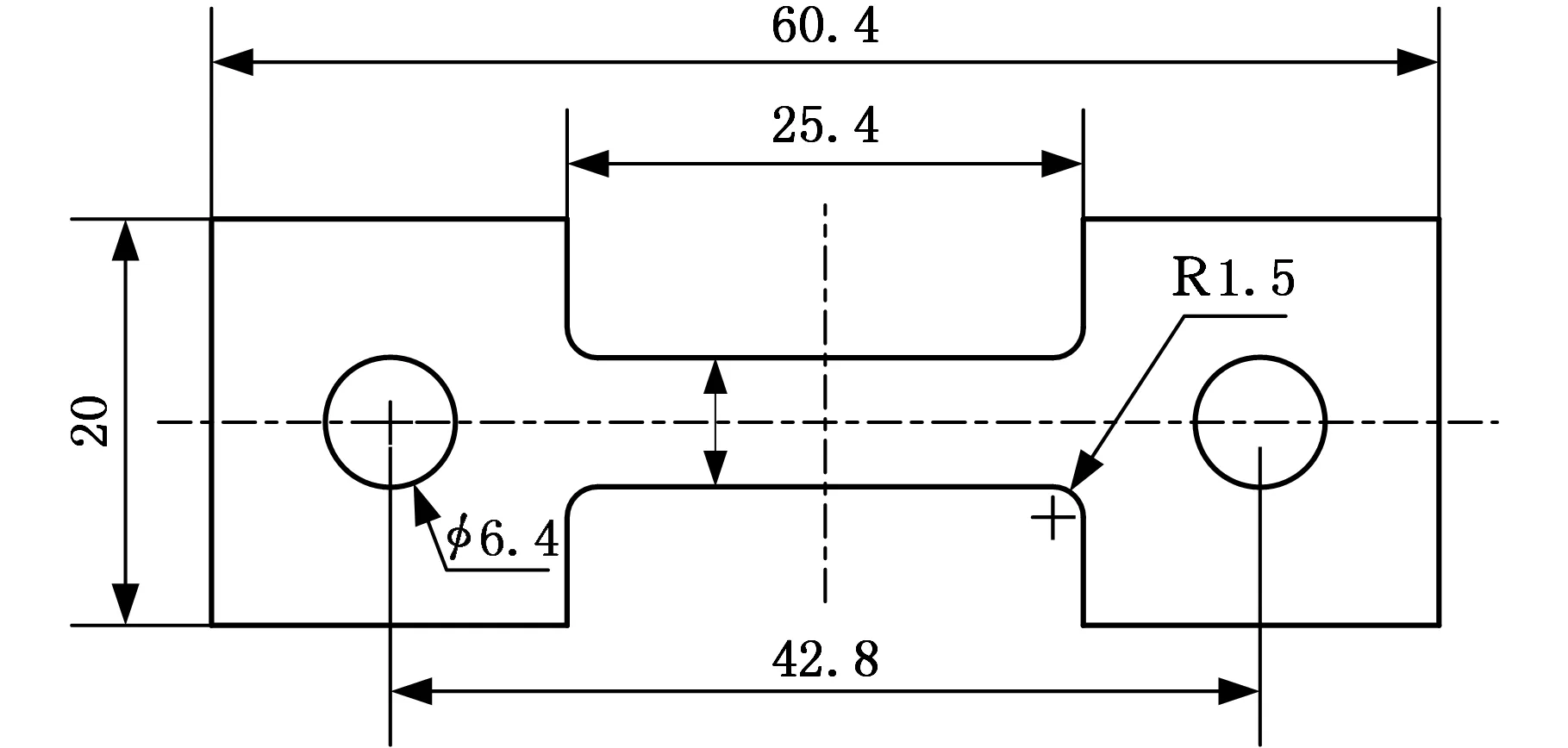
图1 拉伸试样尺寸Fig.1 Tensile specimen size

1.2 单轴拉伸试验

薄板单轴拉伸试验时，需尽可能减小试验误差。试样装夹过程中，维持试样上下两端垂直，避免试样拉伸扭曲。每次拉伸试验前均需先预加适当小载荷后再卸载，以消除试样安装间隙误差并获得准确的拉伸位移。试验采用统一的准静态拉伸(应变速率为0.001 s-1)，将3次重复试验后的平均值作为计算材料真实应力-应变的数据。

单轴拉伸试验目的是为了研究薄板特征尺寸和晶粒大小对材料力学性能的尺寸效应，因此设计了3组试验：①不同材料厚度的单轴拉伸；②不同晶粒尺寸的单轴拉伸；③不同材料厚度和不同晶粒尺寸的单轴拉伸。

2 试验结果与分析

2.1 拉伸屈服强度的尺寸效应研究

2.1.1 材料厚度对磷青铜薄板力学性能的影响

为研究材料厚度对磷青铜薄板力学性能的影响，本文分别选取50 μm、100 μm、250 μm、500 μm和800 μm的薄板进行单轴拉伸试验，获得的厚度对材料力学性能的影响规律曲线如图2所示。

从图2中可以看出，材料的力学性能在厚度方向上存在明显的 “越小越强”尺寸效应，表明磷青铜薄板拉伸时，表面层效应已不再起主导作用，含内禀尺寸的应变梯度效应更为显著。材料内部塑性流动在拉伸载荷作用下出现了局部化现象[14]，产生附加的非均匀塑性变形，此时几何必须位错(geometrically necessary dislocations, GND)将协调材料内部的点阵畸变，在晶粒内部形成位错墙(dislocation wall)即亚晶界(subgrain boundary)，亚晶界的出现将极大增大统计储存位错(statistically stored dislocations, SSD)运动的阻力，使得屈服强度提高[15]。

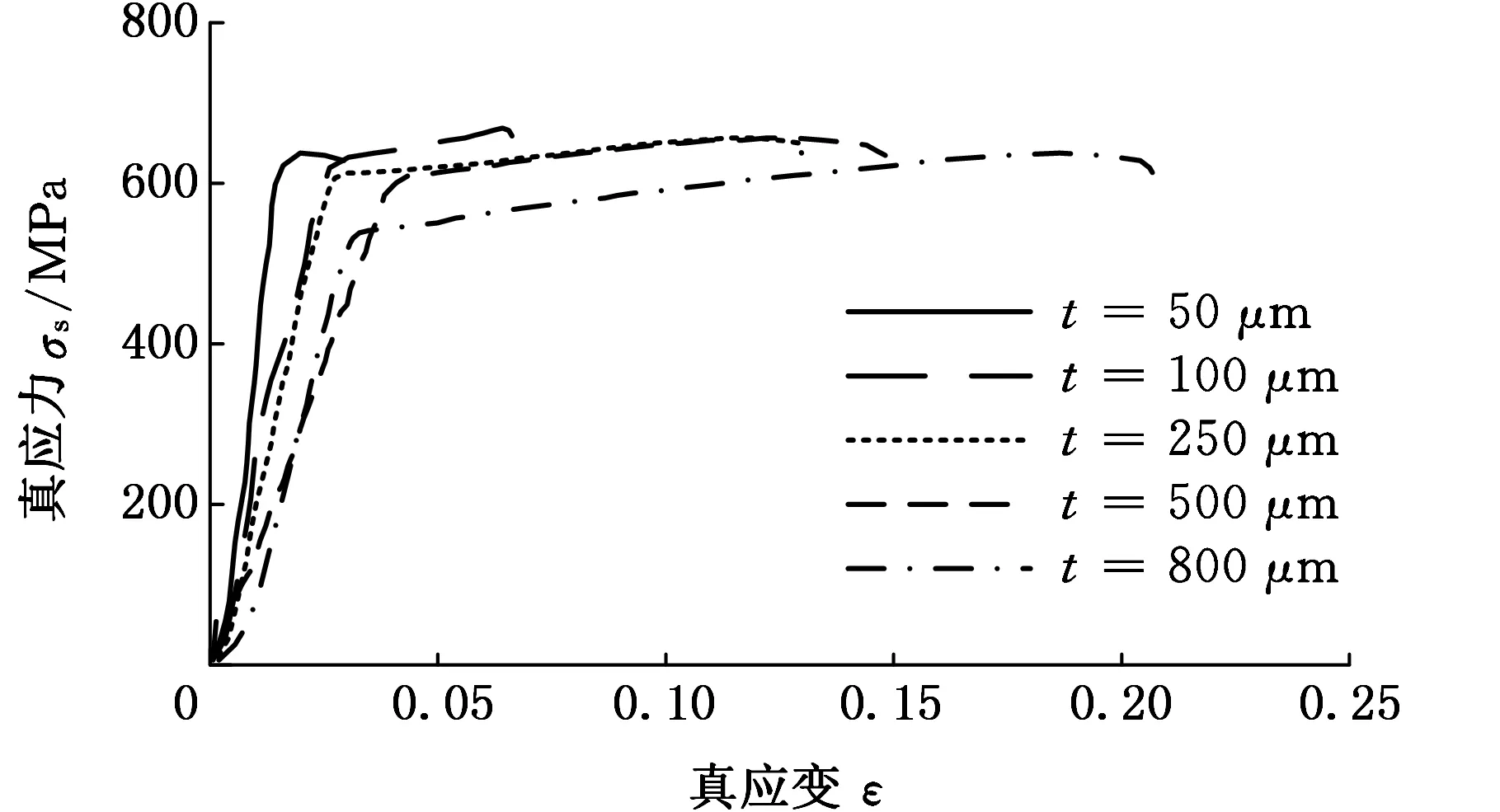
(a)不同厚度试样的拉伸真实力-真应变曲线

(b)屈服强度与厚度的变化关系曲线图2 厚度对材料力学性能的影响规律曲线Fig.2 Relationship between thickness and mechanical properties of thin sheet metal

一般情况下，若不考虑尺寸效应，可采用考虑初始预应力的Ludwik模型来描述材料成形过程中的应变硬化：

(1)

薄板微成形时，受到尺寸效应的影响，不可直接应用Ludwik模型来描述材料的变形行为，需寻求更贴合变形实际的材料模型。

2.1.2 晶粒尺寸对磷青铜薄板力学性能的影响

通过不同温度的退火热处理可获得不同尺寸晶粒的拉伸试样，本文通过研究3种厚度(50μm、100μm和250μm)的薄板在5种不同退火温度下(300 ℃、400 ℃、500 ℃、600 ℃和700 ℃)的拉伸力学性能，获得的晶粒尺寸对材料力学性能的影响规律曲线如图3所示。

可以看出，晶粒尺寸与磷青铜薄板的力学性能表现出“越小越强”的尺寸效应，晶粒尺小越小，其对应的屈服强度越大，呈现出细晶强化现象；在

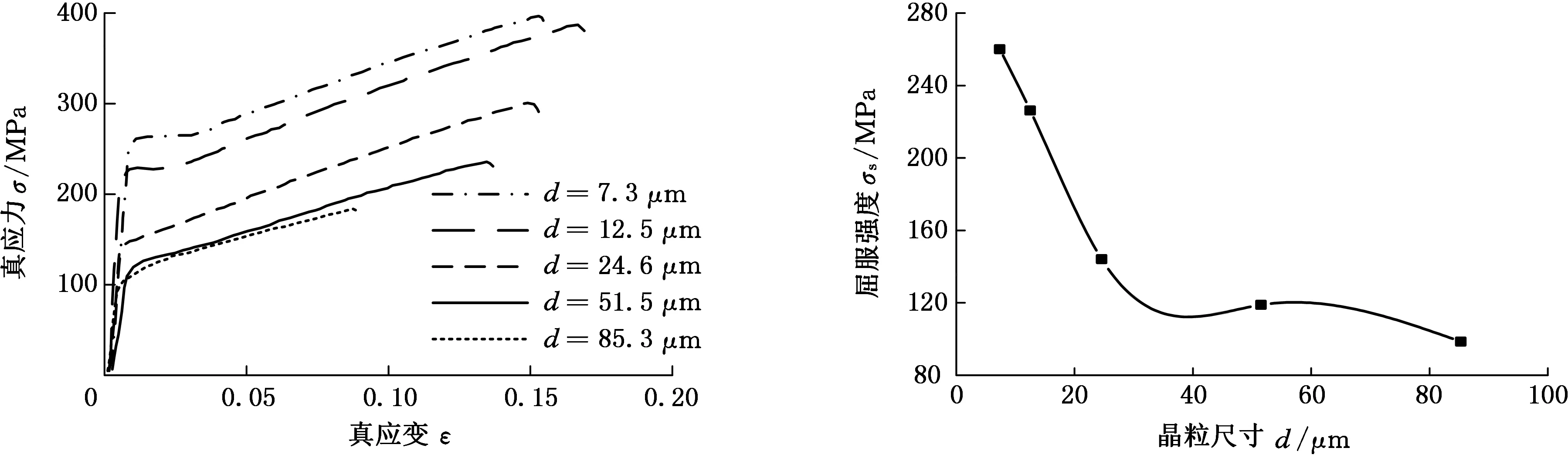
(a)不同晶粒尺寸的拉伸真实力-真应变曲线(t=50 μm) (b)屈服强度与晶粒尺寸的变化关系曲线(t=50 μm)

(c)不同晶粒尺寸的拉伸真实力-真应变曲线(t=100 μm) (d)屈服强度与晶粒尺寸的变化关系曲线(t=100 μm)

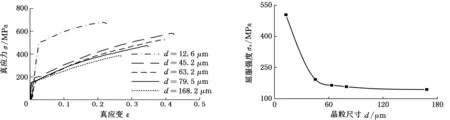
(e)不同晶粒尺寸的拉伸真实力-真应变曲线(t=250 μm) (f)屈服强度与晶粒尺寸的变化关系曲线(t=250 μm)图3 晶粒尺寸对材料力学性能的影响规律曲线Fig.3 Relationship between grain size and mechanical properties of thin sheet metal

材料厚度不变的条件下，晶粒尺寸的增大意味着晶粒减少，t/d<2表明厚度方向已全部为表层晶粒，表层晶粒受内部约束较少，更易滑出自由表面，外在表现为屈服强度的降低[16]。为了进一步研究晶粒大小的尺寸效应，探讨屈服强度与晶粒尺寸之间的定量关系，借助Hall-Petch关系式构建了屈服强度与晶粒尺寸d-0.5的关系曲线，如图4所示。

图4 屈服强度与晶粒尺寸d-0.5的关系曲线Fig.4 Relationship between yield strength and d-0.5

从屈服强度与晶粒尺寸d-0.5的关系曲线可以看出，两者之间存在线性关系(线性相关度超过92.9%)，表明利用Hall-Petch关系式可以描述屈服强度与晶粒尺寸之间的定量关系，如图5所示。

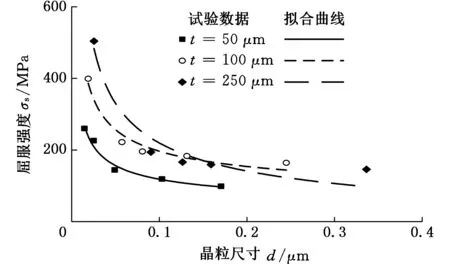
图5 屈服强度与晶粒尺寸的关系曲线Fig.5 Relationship between yield strength and grain size

Hall-Petch关系式作为晶粒强化效应的定量解释，也是最简单的尺寸效应描述，其表达式为

σs(ε)=σ0(ε)+αd-1/2

(2)

式中，σs(ε)为屈服应力；σ0(ε)为初始应力(单个晶粒内部阻碍位错运动的摩擦应力)；α为材料常数(晶界限制应力)。

式(2)适用于多晶体模型，可用来分析晶粒尺寸及晶粒边界对流动应力的影响。ARMSTRONG[17]在Hall-Petch关系式中引入了应变硬化的影响，认为σ0(ε)与单个晶粒的极限抗剪强度有关：

σ0=σsig=MτR

(3)

式中，σsig为单晶体的流动应力；M为方向因子；τR为单个晶粒的极限抗剪强度。

因此，多晶体的流动应力方程可表示为

σ(ε)=σ0+kd-1/2=MτR(ε)+khp(ε)d-1/2

(4)其中，MτR(ε)与单个晶粒的性质有关，khp(ε)d-1/2描述了晶粒间的晶界对流动应力的影响。

由式(4)可以看出，流动应力与晶粒尺寸有一定的对应关系，但并未考虑试样特征尺寸效应的影响，因而对于微成形过程的描述也不准确。

2.1.3t/d对磷青铜薄板力学性能的影响

为了进一步探讨薄板力学性能的尺寸效应，引入材料厚度与晶粒尺寸的比值t/d，从试样横断面积(宽度一定时，简化为材料厚度)所含晶粒数量的角度来研究特征尺寸效应和晶粒大小尺寸效应相互耦合的规律，如图6所示。

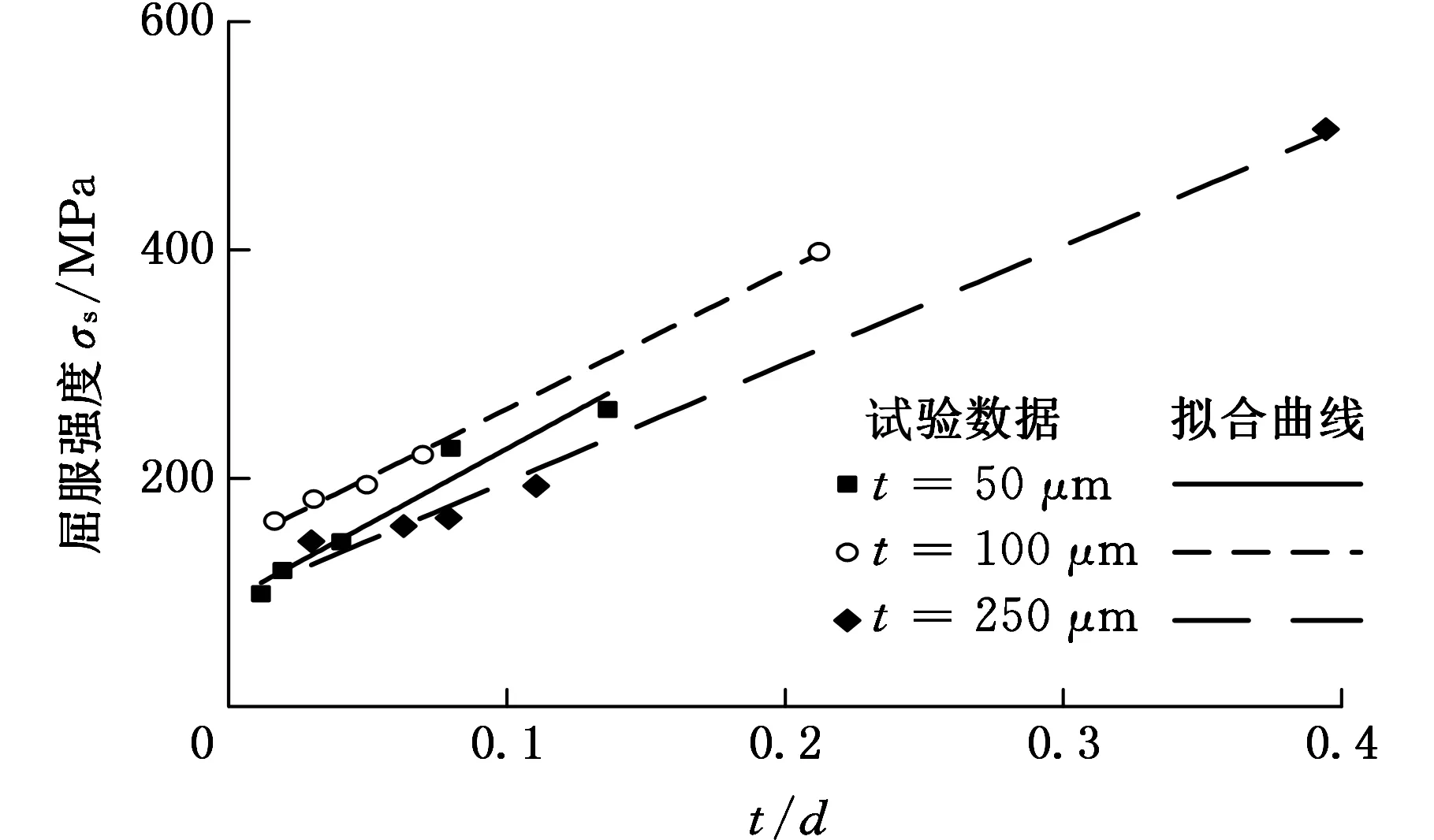
图6 屈服强度与t/d的关系曲线Fig.6 Relationship between yield strength and t/d

从图6中可以看出，薄板流动应力随着t/d的减小而减小。厚度方向上参与变形的晶粒减少，晶粒间的约束也随之减少，变形趋向于单个晶粒的自由变形，单个晶粒的自由变形具有随机性，加剧了变形的不均匀性，流动应力减小；另外，t/d减小可视为表面层晶粒所占比例的相对增大，导致了整体流动应力的减小。

t/d与流动应力之间“越小越弱”的影响规律与表面层模型描述相适应，t/d的减小表明同等厚度方向上的晶粒减少或晶粒尺寸变大，此时表层晶粒所占的比例相对增大，导致整体流动应力减小[18]。因此，借助表面层模型可以在一定范围内描述磷青铜薄板微成形过程中的流动应力变化规律。

2.2 磷青铜薄板拉伸断口形貌分析

借助断口形貌可以定性分析材料的韧性和断裂机制，因此拟通过不同试验条件下磷青铜薄板的拉伸断口形貌分析，探讨介观尺度下的断裂机制，为其成形工艺适应性提供参考。

2.2.1 材料厚度对断口形貌的影响

由图7可以看出，不同厚度的拉伸断口形貌中均有韧窝存在，但随着厚度的减小，韧窝急剧减少。250μm试样的断口形貌中有大量等轴韧窝，韧窝连续、孔洞均匀；50μm试样仅在中间部位存在少量韧窝，边缘区域已出现光滑的滑移特征形貌。表明随着材料厚度的减小，拉伸断裂的机制将从典型的韧窝-微孔聚集型断裂向滑移分离过渡，试样的塑性降低而强度将有所提升。

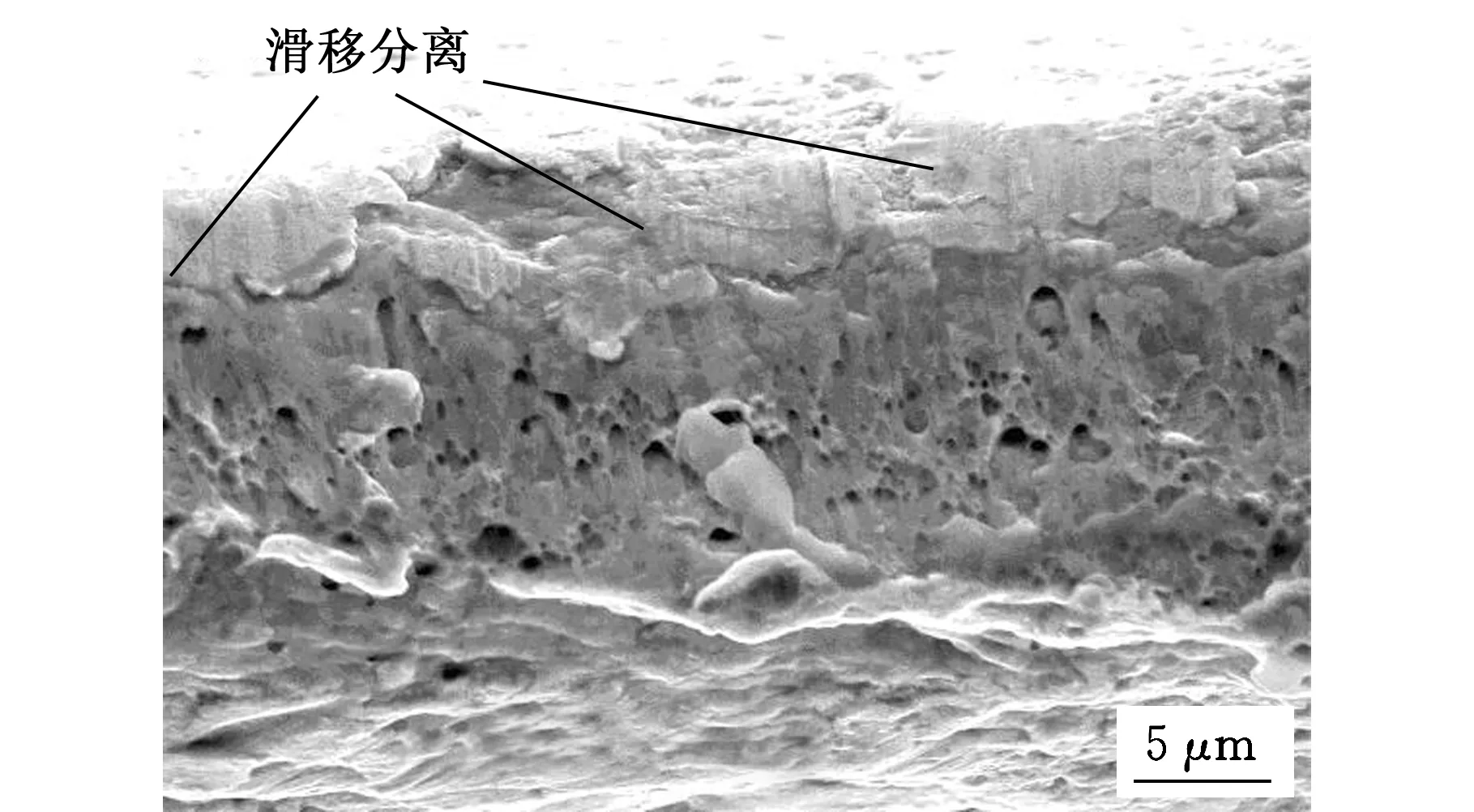
(a)t=50 μm

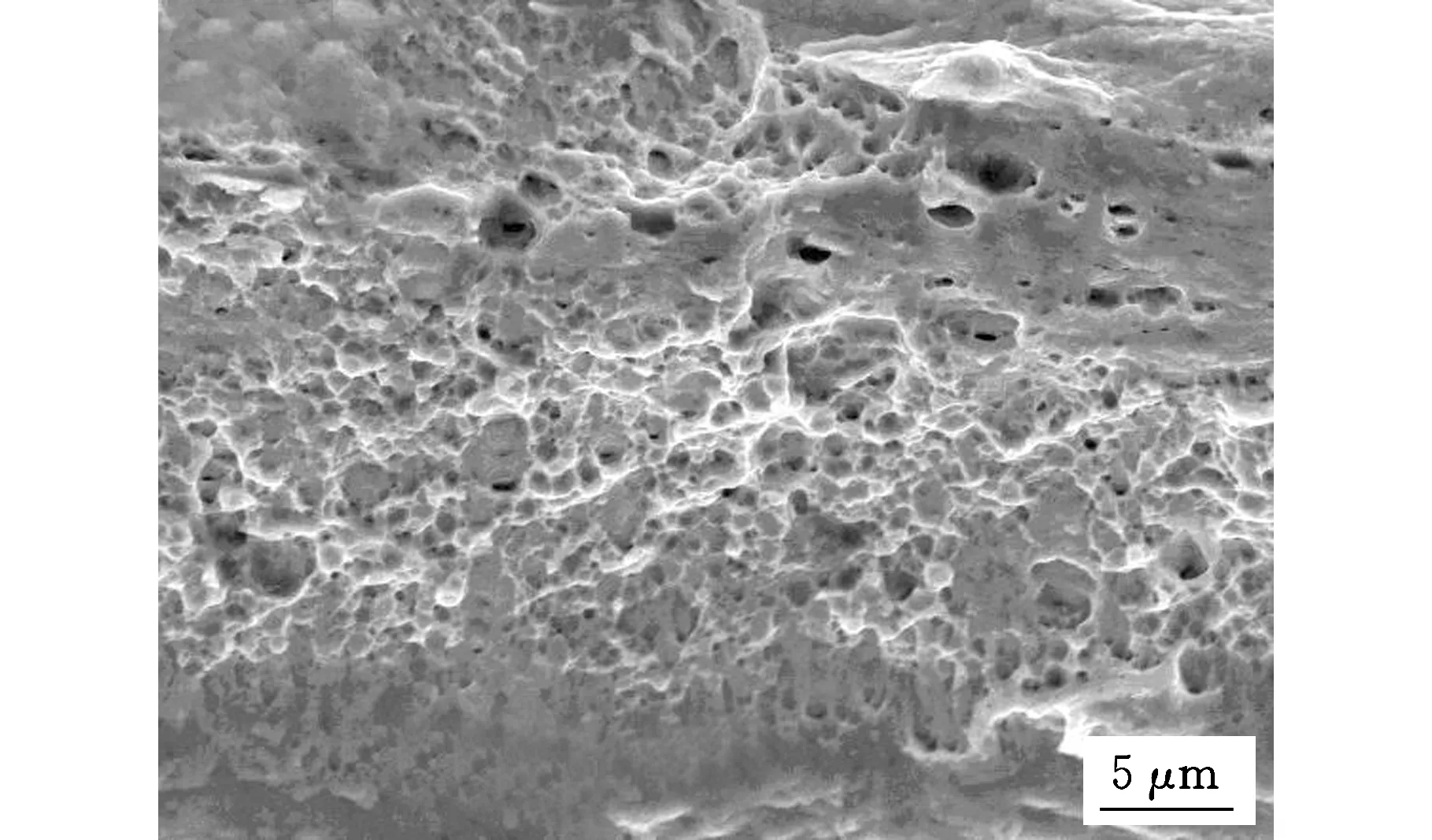
(b)t=100 μm

(c)t=250 μm图7 不同厚度试样的拉伸断口形貌Fig.7 Tensile fracture morphology of specimen atdifferent thickness

2.2.2 晶粒尺寸对断口形貌的影响

(a)d=9.4 μm

(b)d=28.7 μm

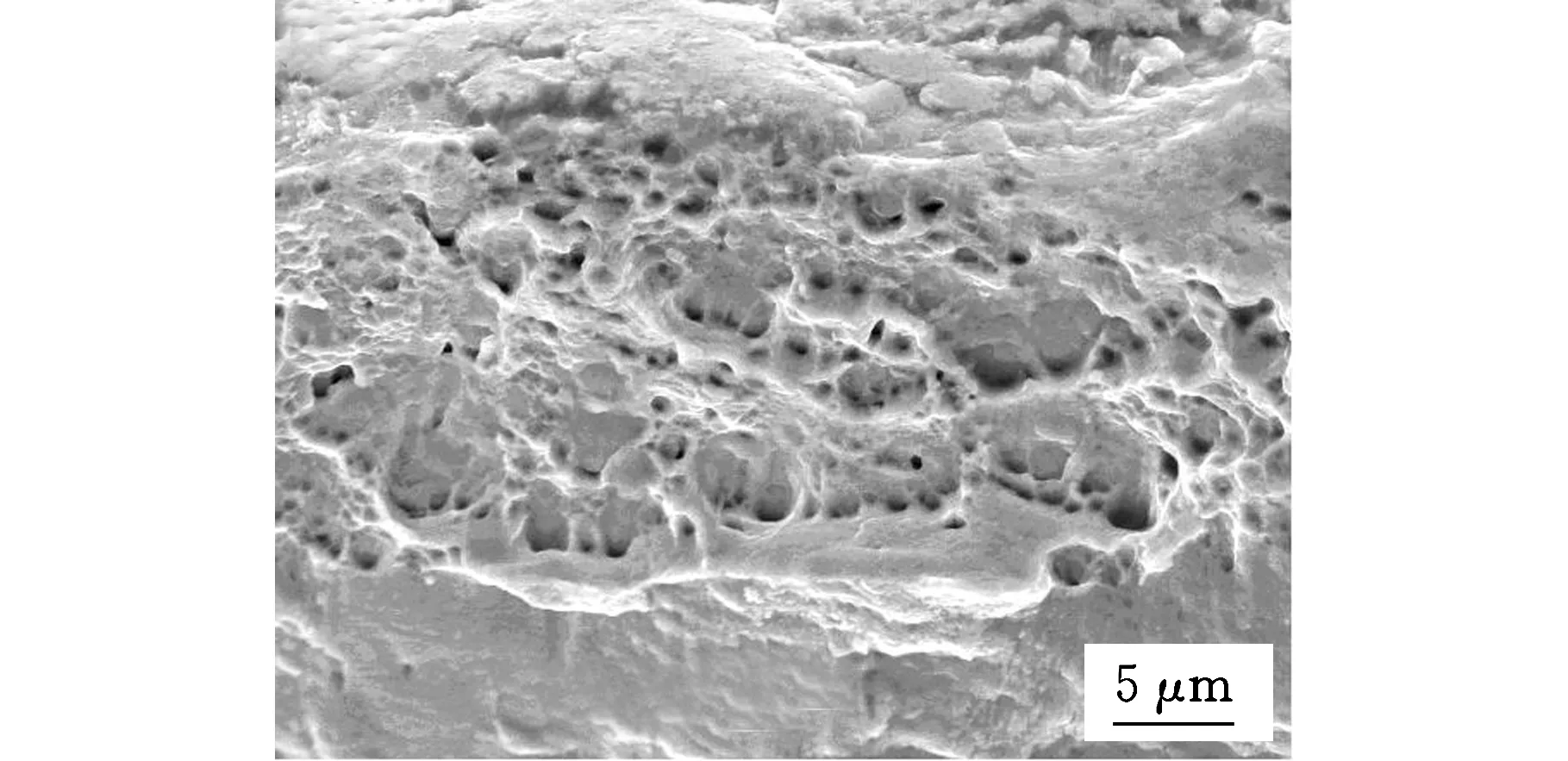
(c)t=40.3 μm

(d)d=65.7 μm

100μm厚度拉伸试样的晶粒尺寸对断口形貌的影响如图8所示。晶粒尺寸随退火温度的提高而增大，断口形貌中的韧窝变大变深，塑性有所增加；但当晶粒尺寸超过试样厚度(图8e)时，拉伸过程中晶粒之间的协调变形便不能或者比较难以进行，造成局部区域的微孔洞更易扩展形成微裂纹，导致试样的迅速断裂[19]。

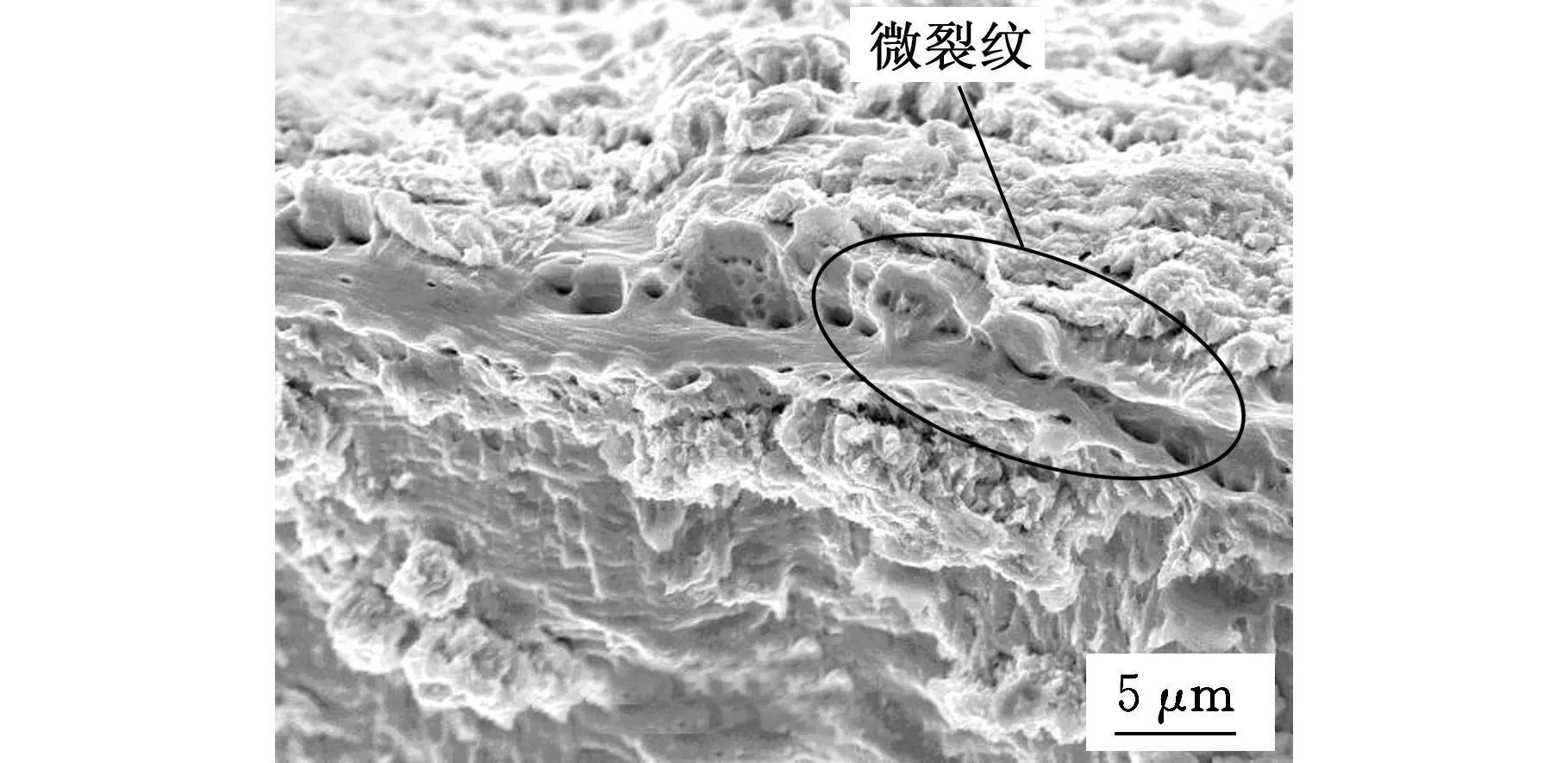
(e)d=122.5 μm图8 不同晶粒尺寸的拉伸断口形貌Fig.8 Tensile fracture morphology of specimen at different grain size

2.3 磷青铜薄板微塑成形本构方程

2.3.1 基于尺寸效应的本构方程的建立

如前所述，磷青铜薄板力学性能随着材料厚度t或晶粒尺寸d的减小而提高，但随着t/d的减小而降低，表现出不同的尺寸效应。根据薄板力学性能的变化规律，将考虑特征尺寸效应的Ludwik模型和考虑晶粒尺寸的Hall-Petch关系式耦合为表面层模型，构建适合于磷青铜薄板微成形的混合本构关系。

2.3.1.1 磷青铜薄板本构关系的建立

参与微成形变形的材料可参考表面层理论[20]，分为表面层和内部层，成形过程中的流动应力与各层在厚度方向上的晶粒数量有直接关系：

σ(ε)=(σs(ε)Ns+σi(ε)Ni)/N

(5)

式中，Ns、Ni分别为表面层和内部层的晶粒数量；N为晶粒数量总和，N=Ns+Ni；σs为符合单晶体模型的表层晶粒流动应力；σi为符合多晶体模型的内部晶粒流动应力。

KIM等[21]、LAI等[22]分别将材料的表面层和内部层简化为单晶体和多晶体：

(6)

式中，m、M分别为单晶体和多晶体的滑移系取向因子；τR(ε)为滑移系上的分解切应力；k(ε)为材料常数。

对于薄板材料，表面层晶粒数量为[23-24]

Ns=[wt-(w-2d)(t-2d)]/A

(7)

式中，w、A分别表示为薄板材料的宽度和单个晶粒的面积。

令η=Ns/N，则Ni/N=1-η。对于薄板材料，存在w≫t和w≫d，因此t/w和d/w的值可忽略不计，故

(8)

将式(3)、式(4)、式(8)代入式(5)，可得

σ(ε)=(Nsσs+Niσi)/N=ηmτR(ε)+

(1-η)(MτR(ε)+khp(ε)d-1/2)

(9)

式中，khp(ε)为材料常数。

KIM等[21]在研究基于表面层模型的本构关系中发现，对于纯铜、铝等典型面心立方晶体材料，多晶体的方向因子M一般取2.6，单晶体的方向因子m一般取2。

将M和m的值代入式(9)，可得

σ(ε)=ησs(ε)+(1-η)σi(ε)=

(10)

2.3.1.2τR(ε)和khp(ε)的确定

借助考虑预应力强化的Ludwik关系式，将τR(ε)和khp(ε)分别表示为[25-26]

(11)

式中，AR、BR、Ahp、Bhp、mR、nhp为常数。

拟合试验所获得的应力-应变曲线，获得AR=48.97，BR=219.65，mR=0.7275，Ahp=325.36，Bhp=1537.36，nhp=0.7275。将系数值代入式(11)可得

(12)

2.3.2本构方程验证

将式(12)代入式(10)可得磷青铜薄板的混合本构关系，并可简化为Ludwik模型：

σ(ε)=a+bε0.7275

(13)

图9为单轴拉伸应力-应变试验数据与式(13)拟合曲线，可以看出，二者吻合度较高，验证了所获得磷青铜薄板混合本构关系的合理性。

(a)t=50 μm

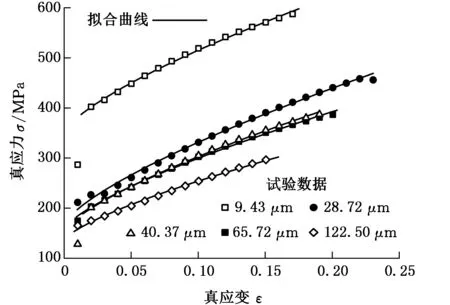
(b)t=100 μm图9 试验数据与模型拟合的比较Fig.9 Comparison of experimental data and fitting curves

3 结论

(1)对厚度分别为50μm、100μm、250μm、500μm和800μm的磷青铜薄板试样进行了单轴拉伸试验，探讨了试样厚度的尺寸效应。结果表明：材料的屈服强度随着试样厚度的减小而增大，表现出“越小越强”的第Ⅱ类尺寸效应；随着试样厚度的减小，拉伸断裂的机理逐渐由韧窝-微孔聚集断裂向滑移分离过渡。

(2)对厚度为50μm、100μm、250μm，退火温度为300 ℃、400 ℃、500 ℃、600 ℃和700 ℃的磷青铜薄板进行了单轴拉伸试验，探讨了晶粒的尺寸效应。结果表明：材料的屈服强度随着晶粒尺寸的减小而增大，表现出“越小越强”的第Ⅱ类尺寸效应；材料的屈服强度随着t/d的减小而降低，表现出“越小越弱”的第Ⅰ类尺寸效应；随着晶粒尺寸的增加，拉伸断口中的韧窝形状逐渐变大变深，但当晶粒尺寸超过试样厚度时，拉伸过程中过早形成的微裂纹将导致试样迅速断裂。

(3)基于表面层模型，将薄板材料表层晶粒视为单晶，内部晶粒看作多晶，构建适合于磷青铜薄板微成形的混合本构方程。

[1] 孙军,刘刚,丁向东.介观尺度铜膜力学行为尺度效应研究进展[J].中国材料进展, 2009, 28(1):49-53. SUN Jun, LIU Gang, DING Xiangdong. Progress in the Size-dependent Mechanical Properties of Cu Films at Mesoscale[J]. Materials China, 2009, 28(1):49-53.

[2] LEOPOLD J. Foundations of Micro Forming[C]// Proceedings of the 6th ICTP. Nuremberg, 1999:889-894.

[3] 彭林法,李成锋,来新民,等.介观尺度下的微冲压工艺特点分析[J].塑性工程学报,2007,14(4):54-59. PENG Linfa, LI Chengfeng, LAI Xinming, et al. Characteristic Analysis of Stamping Process in Miceo/Meso Scale[J]. Journal of Plasticity Engineering, 2007, 14(4):54-59.

[4] FU M W, CHAN W L. Flow-induced Defects in Mesoforming Processes[M]. London:Springer, 2014:131-149.

[5] VOLLERTSEN F, NIEHOFF H S, HU Z. State of the Art in Micro Forming[J]. International Journal of Machine Tools & Manufacture, 2006, 46(11):1172-1179.

[6] HOFFMANN H, HONG S. Tensile Test of Very Thin Sheet Metal and Determination of Flow Stress Considering the Scaling Effect[J]. Annals of the CIRP, 2006, 55(1):417-423.

[7] ENGEL U, ECKSTEIN R. Microforming—from Basic Research to Its Realization[J]. Journal of Materials Processing Technology, 2002, 125/126(2):35-44.

[8] KALS R, VOLLERTSEN F, GEIGER M. Scaling Effects in Sheet Metal Forming[C]//Proceedings of the 4th International Conference of Sheet Metal. Enschede, 1996:65-75.

[9] KALS T A, ECKSTEIN R. Miniaturization in Sheet Metal Working[J]. Journal of Materials Processing Technology, 2000, 103(1):95-101.

[10] RAULEA L V, GOIJAERTS A M, GOVAERT L E, et al. Size Effects in the Processing of Thin Metal Sheet[J]. Journal of Materials Processing Technology, 2001, 115:44-48.

[11] GEIGER M, ECKSTEIN R. Microforming:Advanced Technology of Plasticity[C]//Proceedings of the 7th ICTP. Yokohama, 2002:327-338.

[12] PERNIN N, CHEMBERT J, PICART P. Modeling of Micro-forming by Plasticity Gradient and Surface Layer Methods[C]//8th International Conference on Material Forming. Cluj-Napoca, 2005:109-112.

[13] 刘平, 任凤章, 贾淑果. 铜合金及其应用[M]. 北京:化学工业出版社, 2007. LIU Ping, REN Fengzhang, JIA Shuguo. Copper Alloy and Its Application[M]. Beijing:Chemical Industry Press, 2007.

[14] 陈少华, 冯彪. 单轴拉伸下剪切带的应变梯度理论预测[C]//塑性力学新进展——2011年全国塑性力学会议. 北京, 2011:99-105. CHEN Shaohua, FENG Biao. Theoretical Prediction of Strain Gradient of Shear Zone under Uniaxial Tension[C]//New Progress of Plastic Mechanics—2011 National Conference on Plastic Mechanics. Beijing, 2011:99-105.

[15] 周健. 铜箔力学性能的尺寸效应及微拉深成形研究[D]. 哈尔滨:哈尔滨工业大学, 2010. ZHOU Jian. Research on Size Effects of Mechanical Property and Micro Deep Drawing of Copper Foil[D]. Harbin:Harbin Institute of Technology, 2010.

[16] 黄晓旭. 金属强度的尺寸效应[J]. 金属学报, 2014, 50(2):137-140. HUANG Xiaoxu. Size Effects on the Strength of Metals[J]. Acta Metallurgica Sinica, 2014, 50(2):137-140.

[17] ARMSTRONG R W. Theory of the Tensile Ductile-brittle Behavior of Poly-crystalline h.c.p. Materials, with Application to Beryllium[J]. Acta Metallurgica, 1968, 16(3):347-355.

[18] 郭斌, 周健, 单德彬, 等. 黄铜箔拉伸屈服强度的尺度效应[J]. 金属学报, 2008, 44(4):419-422. GUO Bin, ZHOU Jian, SHAN Debin, et al. Size Effects of Yield Strength of Brass Foil in Tensile Test[J]. Acta Materialia, 2008, 44(4):419-422.

[19] 刘芳, 魏子云, 李跃凯. 微细黄铜板料尺寸效应[J]. 塑性工程学报, 2010, 17(6):18-22. LIU Fang, WEI Ziyun, LI Yuekai. Size Effects Research on the Micro Sheet Metal H62 Brass[J]. Journal of Plasticity Engineering, 2010, 17(6):18-22.

[20] GEIGER M, VOLLERTSEN F, KALS R. Fundamentals on the Manufacturing of Sheet Metal Microparts[J]. Annals of the CIRP, 1996, 45(2):227-282.

[21] KIM G Y, KOC M, MAYOR R, et al. Modeling of the Semi-solid Material Behavior and Analysis of Micro/Meso-scale Feature Forming[J]. Journal of Manufacturing Science & Engineering, 2007, 129(2):237-245.

[22] LAI X M, PENG L F, HU P, et al. Material Behavior Modeling in Micro/Meso-scale Forming Process with Considering Size/Scale Effects[J]. Computational Materials Science, 2008, 43(4):1003-1009.

[23] JANSSEN P J M, KEIJSER T H D, GEERS M G D. An Experimental Assessment of Grain Size Effects in the Uniaxial Straining of Thin Al Sheet with a Few Grains Across the Thickness[J]. Materials Science & Engineering A, 2006, 419(1/2):238-248.

[24] 董培龙. 微塑性成形本构关系及超薄板微弯曲成形研究[D].镇江:江苏大学, 2009. DONG Peilong. Study on the Constitutive Behavior in Micro Forming and Micro Bending of Ultra-thin Sheet[D]. Zhenjiang:Jiangsu University, 2009.

[25] 李明星. SUS304不锈钢箔微冲裁尺寸效应研究[D]. 哈尔滨:哈尔滨工业大学, 2011. LI Mingxing. Research on Size Effect in Micro Blanking of SUS304 Stainless Steel Foil[D]. Harbin:Harbin Institute of Technology, 2011.

[26] 孟庆当, 李河宗, 董湘怀,等. 304不锈钢薄板微塑性成形尺寸效应的研究[J]. 中国机械工程, 2013, 24(2):280-283. MENG Qingdang, LI Hezong, DONG Xianghuai, et al. Investigation of Size Effects of 304 Stainless Steel Foils in Microforming Process[J]. China Mechanical Engineering, 2013, 24(2):280-283.

(编辑 张 洋)

Size Effects of Deformation Behaviour and Ductile Fractures in Meso-scale Thin Sheet Metal of Phosphor Bronze

WANG Lei1HU Daochun2

1.School of Mechanical Engineering,Taizhou University,Taizhou,Zhejiang，318000 2.College of Mechanical and Electrical Engineering,Taizhou Vocational & Technical College, Taizhou,Zhejiang，318000

Size effects of mechanics properties and ductile fractures for ultra thin sheet metal of phosphor bronze sheet were studied by uniaxial micro tensile test. Experimental results show that yield strength has second order size effeets with metal thicknesstand grain sized， and has first order size witht/d. Fracture surface shows that the fracture mechanism is composed of transitions from dimple-microvoids accumulation fractures to slip separation with the material thicknesses decrease, and dimple morphology becomes larger and deeper with the increases of grain sizes, but whent/d<1, initiation of micro cracks is geminated, and fracturs are occurred immediately. At last, a hybrid constitutive equation was established based on surface layer model.

phosphor bronze; fractography analysis; yield strength; size effect

2016-06-06

浙江省自然科学基金资助项目(LY15E060003)；浙江省教育厅科研项目(Y201636389)；台州职业技术学院重点课题(2016ZD02)

TG301;TG146.1

10.3969/j.issn.1004-132X.2017.08.018

王 蕾，女，1978年生。台州学院机械工程学院讲师。主要研究方向为材料成形性能分析与评价、板料成形CAE技术。发表论文20余篇。胡道春(通信作者)，男，1977年生。台州职业技术学院机电工程学院副教授。E-mail:springer_1028@163.com。