有色噪声激励下非线性吸振器的能量传递
刘丽兰 任博林 李淑超 张小静
西安理工大学机械与精密仪器工程学院,西安,710048
有色噪声激励下非线性吸振器的能量传递
刘丽兰 任博林 李淑超 张小静
西安理工大学机械与精密仪器工程学院,西安,710048
将双稳态振子作为非线性吸振器,建立了含非线性吸振器的主系统力学模型,给出了有色噪声激励下系统的控制方程并进行了量纲一化。借助数值仿真,研究了系统初值、调谐频率比、质量比、阻尼系数对主系统和非线性吸振器振动能量的影响规律。通过系统结构参数的逐步优化选择,获得了将主系统振动能量最小化并使非线性吸振器振动能量最大化的最优结构参数配置区间。
有色噪声;非线性吸振器;质量比;调谐频率比;参数优化
0 引言
非线性吸振器可以较好地从线性主系统吸收能量,已应用到各个领域[1-2]。国内外学者对非线性吸振器的研究做了很多工作。STAROSVETSKY等[3]提出了在线性系统中连接强非线性能量收集器来抑振的力学模型,并证明该非线性吸振器比线性吸振器有更好的抑振效果。AHMADABADI等[4]用非线性能量吸振器来控制悬臂梁的非线性振动,减小了悬臂梁的振动能量,且非线性吸振器的能量不会逆向传递到悬臂梁系统。MADHAV等[5]采用平稳高斯白噪声激励,研究了吸振器在随机激励下捕获能量的有效性,研究表明,随机激励下的非线性吸振器可减小主结构的振动,且具有较好的减振效果。张也弛等[6-7]研究了非保守系统中的靶能量的传递情况,研究结果表明,非保守系统只有在特定初始条件下,吸振器才能吸收主系统的振动能量。熊怀等[8]研究了阻尼对耦合非线性能量阱系统的影响,获得了非线性能量阱具有吸振能力时线性振子阻尼的有效范围,并通过数值分析验证了研究结果。
目前,非线性吸振器的研究多侧重于简谐激励和白噪声随机激励。理想的白噪声在物理上是很难实现的。工程结构受自身结构及阻尼的影响,会将随机噪声激励过滤为有色噪声,因而研究有色噪声激励下非线性吸振器系统的动力学响应具有重要意义。
1 非线性吸振器系统力学模型
本文研究的非线性吸振器系统的力学模型如图1所示。其中,m2为主系统的质量;m1为永磁铁的质量;y(τ)为主系统的绝对位移;x(τ)为电磁铁与主系统之间的相对位移;dU/dx为吸振器的双稳态弹簧恢复力,dU/dx=-k1x+k3x3;U为非线性弹簧的弹性势能;k1、k3分别为吸振器的线性刚度系数和非线性刚度系数;c1、c2分别为非线性吸振器和主系统的阻尼;k2为主系统的刚度;Ys为施加给主系统的外部随机激振力。永磁铁不仅能吸收主系统的振动,如果增加线圈绕组,还可以利用磁铁与线圈间的相对运动进行发电,充分地利用振动能量。非线性吸振器系统的系统控制方程为
(1)
(2)

图1 非线性吸振器系统的力学模型Fig.1 Mechanical model of nonlinear vibration absorber system
对式(1)、式(2)进行量纲一化,得到
(3)
(4)
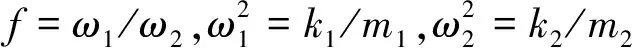
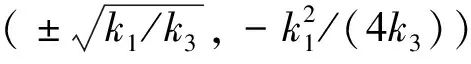

图2 非线性势能函数示意图Fig.2 Schematic of nonlinear potential energy function
2 有色噪声数学模型
高斯白噪声是被广泛应用的一种随机激励,但其经过大型结构滤波后带宽变窄;所以本文研究有色噪声激励下主系统和非线性吸振器系统间的振动能量传递情况。
模拟的高斯白噪声由独立的单位正态随机序列ξ来表示:
(5)
其中,D为噪声强度,Δt为时间间隔,R(1,N)为N个符合正态分布的随机数。有色噪声Y可以看成是由白噪声序列ξ驱动的线性环节的输出[9]:
Y(i+1)=h1ξ(i)-(h1r-1)Y(i)
(6)
有色噪声激励Y有一个相关函数〈Y(t)Y(t*)〉=rDexp(-r|t-t*|),其中,r为有色噪声的带宽,t*为初始时间,常数。
利用1阶Langevin方程可以产生有色噪声[10-11]:
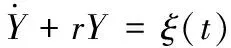
(7)
〈ξ(t)〉=0
(8)
〈ξ(t)ξ(t*)〉=δ(t-t*)
(9)
利用Euler差分格式求解式(7)~式(9),即可得到有色噪声信号,如图3所示。
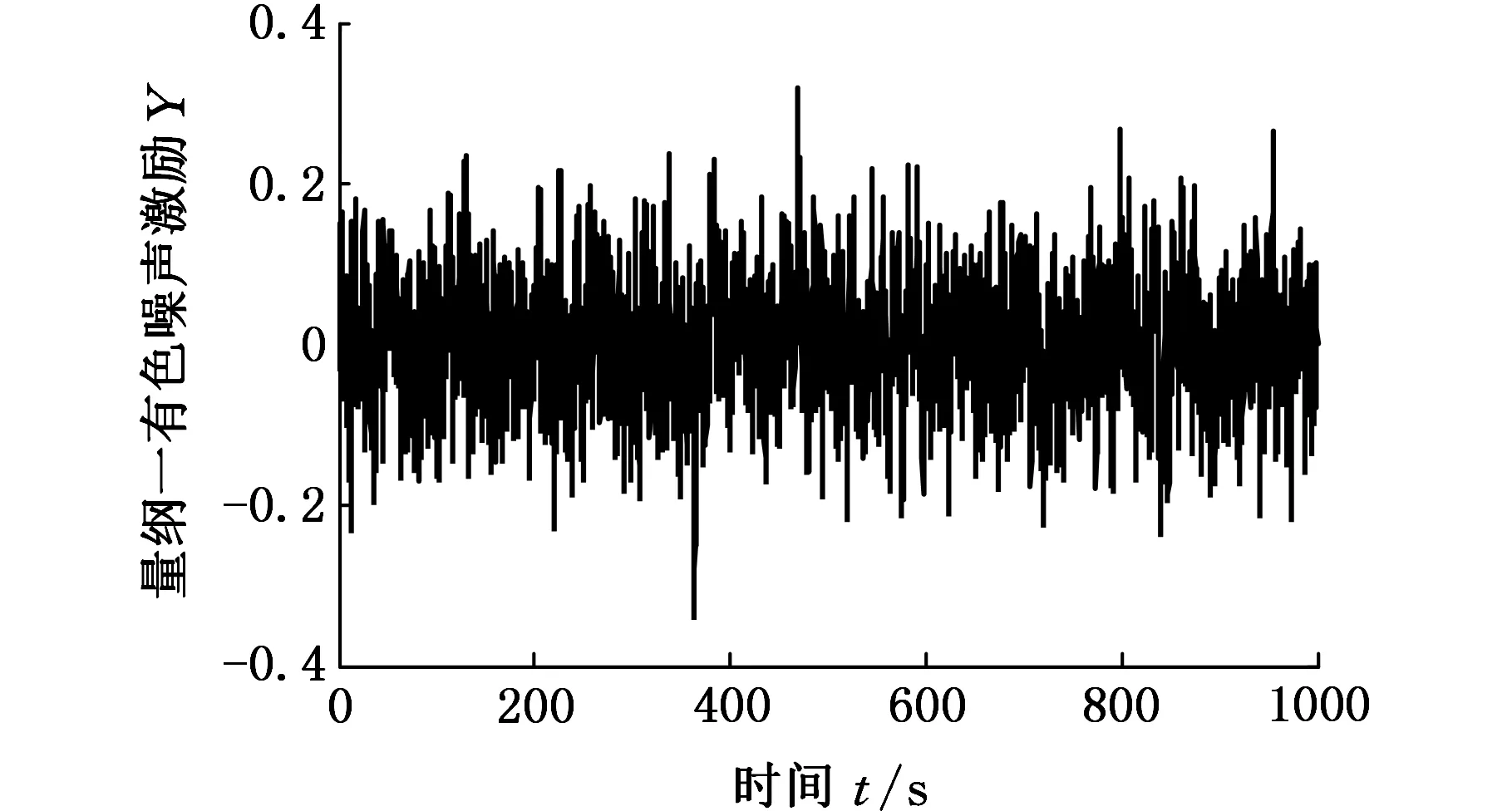
图3 有色噪声Fig.3 Colored noise
3 利用Euler差分格式求解微分方程
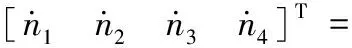
(10)
将(10)式改写为Euler差分格式:
(11)
tn+1=tn+Δt
4 主系统和吸振器的振动能量
吸振器的主要目的是吸收外部激励的能量从而减小主系统的振动,吸振器性能的好坏直接取决于系统的结构参数配置,因此本文主要研究系统初值和结构参数对系统振动能量的影响。
非线性吸振器能量为
(12)
主系统能量为
(13)

(14)
(15)
两振子的平均振动能量分别为
(16)
(17)
由式(14)、式(15)可以看出,非线性吸振器和主系统的能量直接取决于两者的位移和速度响应。下面分别从两个方面进行研究:①系统结构参数保持不变,有色噪声强度取定值,分析系统初值对主系统和非线性吸振器振动能量的影响;②在前面研究的基础上,选取非线性吸振器工作性能较好的系统初值,分析系统结构参数配置对主系统和非线性吸振器振动能量的影响。
5 系统初值对振动能量的影响

从图4中可以看出,随着主系统初值的增大,主系统和非线性吸振器系统的能量均发生了较大变化,吸振器吸收的能量波动较大。总的来看,当系统初值x2为0和0.5时,主系统将大部分能量传递给非线性吸振器,主系统的振动能量最小,相比之下,非线性吸振器系统的能量较大,且随时间变化较为稳定,吸振效果较佳,如图4a、图4b所示。

(a)x2=0
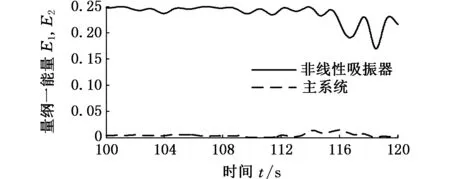
(b)x2=0.5
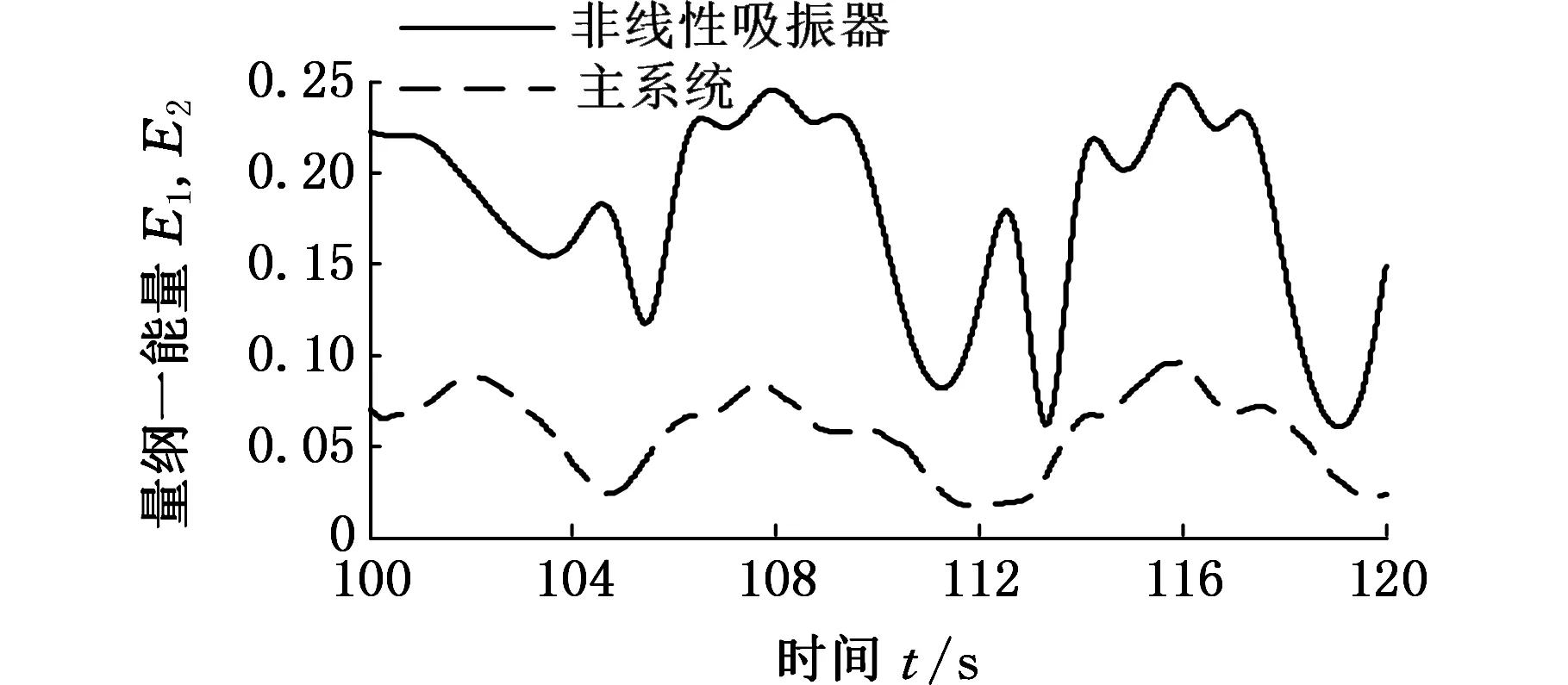
(c)x2=1.5
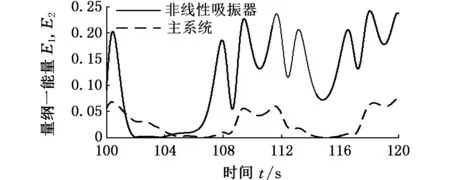
(d)x2=2.0

(e)x2=3.0
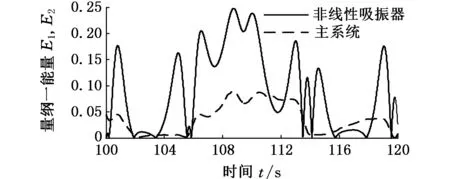
(f)x2=3.5图4 非线性吸振器和主系统之间的能量传递Fig.4 Energy transfer between nonlinear absorber
进一步对比图4a、图4b可以发现,x2=0.5时,主系统振动能量处于最小值,非线性吸振器吸收能量最大且波动最小,吸振效果最佳。
结合图4c~图4f可以发现,随着初值的增大,非线性吸振器吸收的能量波动较大,虽然在x2=3.5时(图4f),非线性吸振器吸收的瞬时能量达到最大值0.25,但主系统振动能量也偏大,非线性吸振器不能有效吸收主系统能量,无法有效减振。同样,x2为1.5,2.0,3.0时,主系统振动能量均偏大,故此初值不利于非线性吸振器系统吸收外部激振能量。
6 系统参数对能量传递的影响
非线性吸振器对结构参数的变化较为敏感,为找到使主系统振动最小且吸振器工作状态最佳(最利于发电状态)的结构参数配置范围,本文研究了调谐频率比、质量比和非线性吸振器的阻尼系数对系统振动能量的影响,并找出最优的参数配置区间。
(1)其他结构参数保持不变,仅变化调谐频率比,来分析最佳调谐频率比参数配置区间;
(2)在前面研究基础上,将最佳调谐频率比区间中的某一频率作为最佳调谐频率,其他结构参数保持不变,仅变化质量比,来分析最佳质量比参数配置区间;
(3)在前面研究基础上,选择最佳调谐频率比和最佳质量比区间中的某个频率和某个质量比,其他结构参数仍保持不变,仅变化阻尼系数,来分析最佳阻尼系数配置区间。
6.1 最佳调谐频率比分析
取系统参数β=1,μ=0.3,γ1=γ2=0.05,计算时间为200~1000 s ,利用式(16)、式(17)求出两振子的平均能量,非线性吸振器和主系统的平均振动能量随调谐频率比f的变化见图5。

图5 能量变化曲线图Fig.5 Curve of energy change
从图5中可以看出,随着调谐频率比f的增大,主系统振动平均能量出现了先减小后增大的趋势;非线性吸振器出现了上升→下降→上升的总体趋势,f为0.2~0.4时出现平均能量的最大值,综合考虑,选取区间0.2~0.4为调频比的最佳配置区间。
为更加详细且直观地分析主系统和非线性吸振器的能量传递及动力学响应,不失一般性,选取f=0.3进行数据分析。图6为主系统和非线性吸振器的振动能量响应图、时域图和相图。
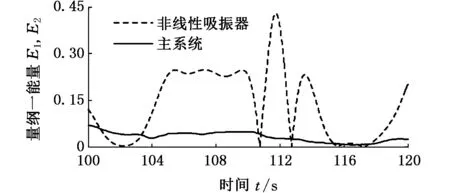
(a)振动能量响应图

(b)时域图
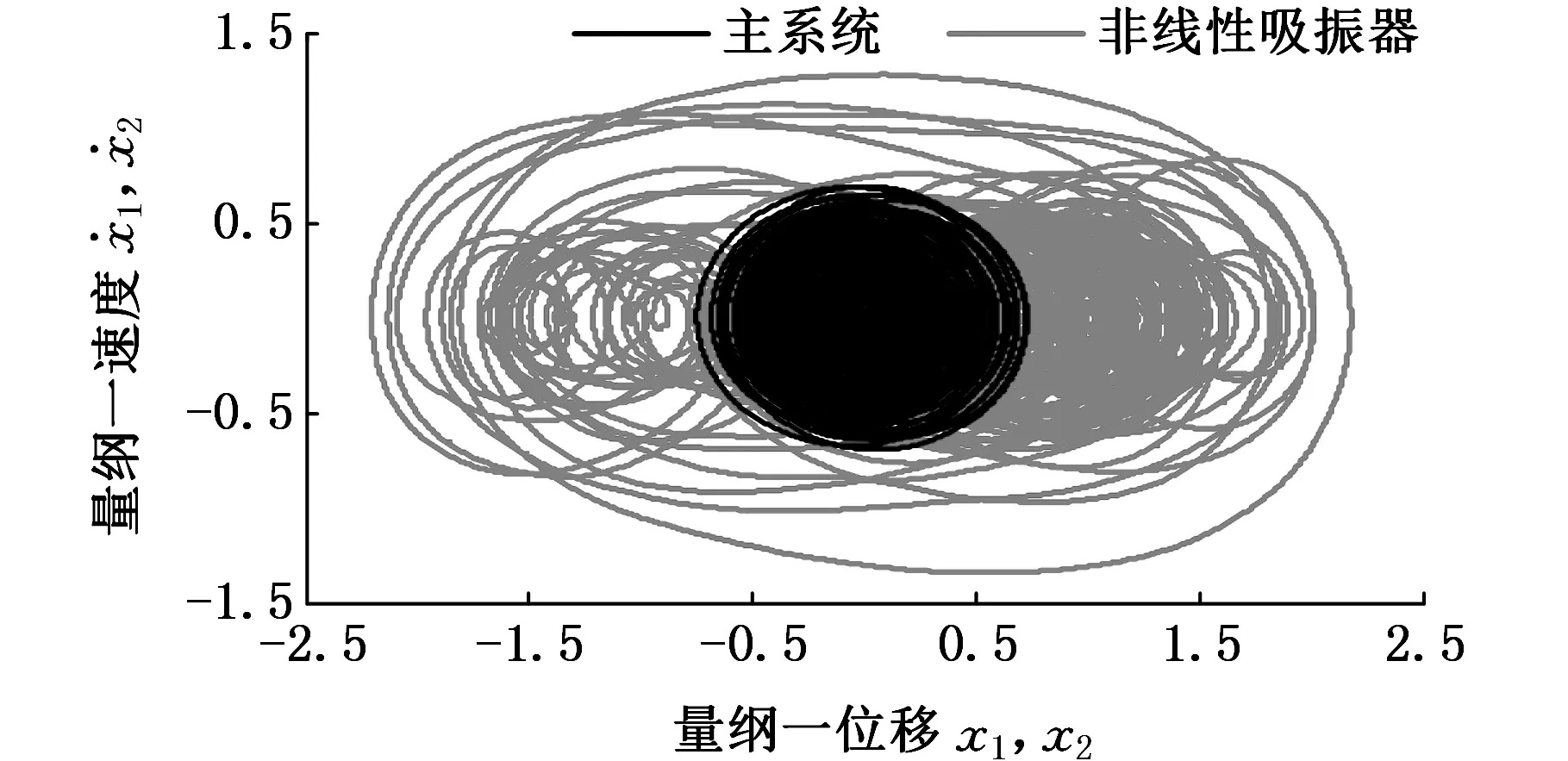
(c)相图图6 系统能量及位移响应图 (f=0.3,β= 1.0,μ=0.3,γ1=γ2=0.05)Fig.6 Diagram of system energy and displacement response (f=0.3,β= 1.0,μ=0.3,γ1=γ2=0.05)
从图6a中可看出,主系统振动能量比非线性吸振器的振动能量小得多,非线性吸振器吸收了大部分能量,实现减振。从图6b、图6c中可看出,主系统在零平衡点附近做小幅运动的同时,非线性吸振器在2个稳定平衡点之间多次越过势垒,做大幅混沌运动,处于最佳减振状态。
6.2 最佳质量比分析
在6.1节调谐频率比研究的基础上,选取β=1,f=0.3,γ1=γ2=0.05,研究质量比μ对系统的能量传递影响,图7所示为非线性吸振器和主系统的平均能量随质量比的变化曲线。
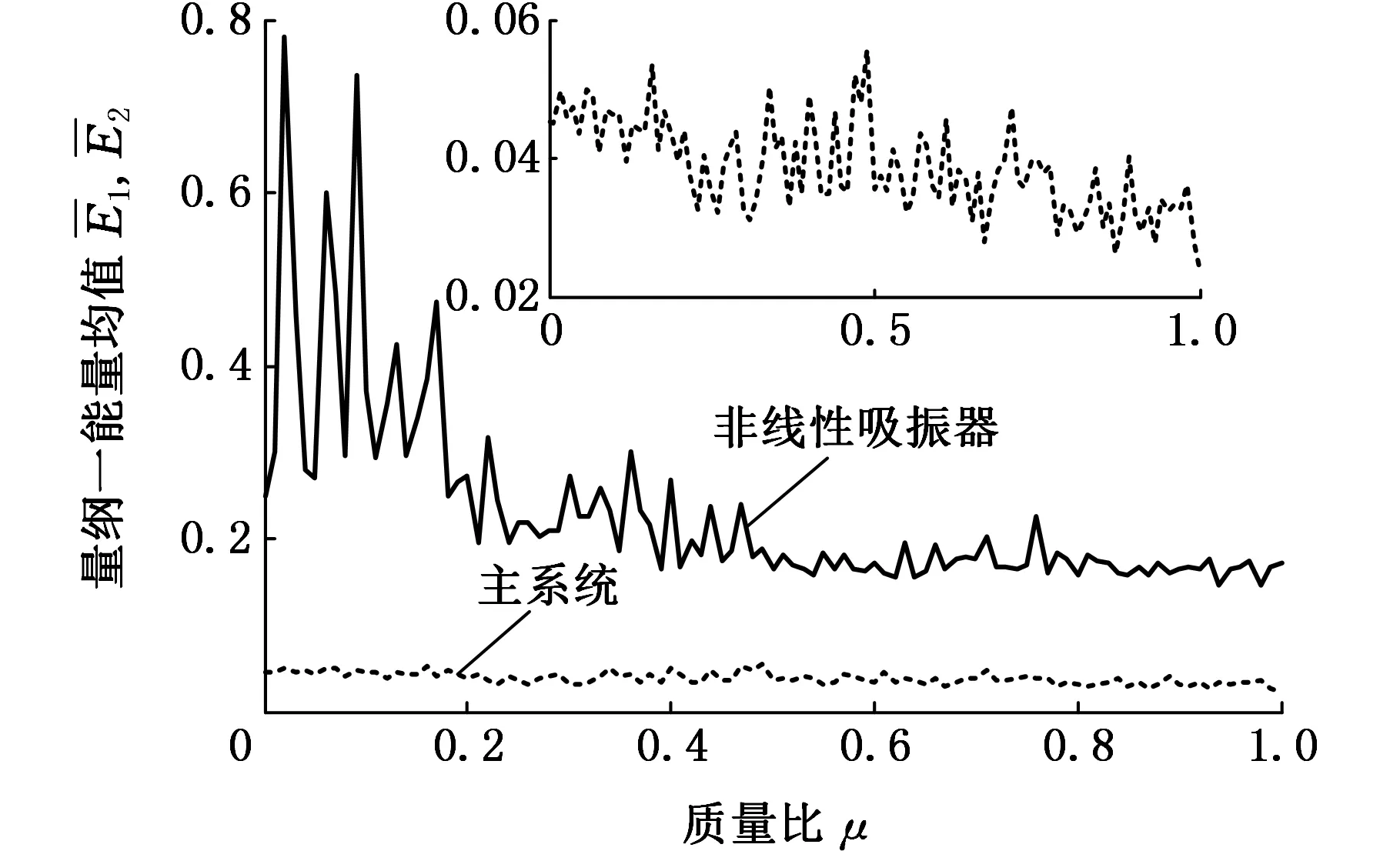
图7 能量变化曲线图Fig.7 Curve of energy change
从图7中可看出,主系统平均能量一直较小,基本保持在0.05附近。非线性吸振器的振动能量在质量比较小时出现最大值,之后逐渐趋于恒定,综合考虑,选0.02~0.15为μ的最佳质量比配置区间。
同样取配置区间中的μ=0.1进行分析,主系统和非线性吸振器的振动能量及动力学响应如图8所示。从图8a中可以看出,主系统的振动能量在小范围内波动(比非线性吸振器的振动能量小得多),非线性吸振器吸收了大部分能量,实现了减振。从图8b、图8c中可看出,主系统在零平衡点附近做小幅运动的同时,非线性吸振器在2个平衡点之间越过势垒,做大幅混沌运动。对比图6c可知,非线性吸振器越过势垒做大幅混沌运动的次数增多,更有利于发电。
6.3 最佳阻尼系数分析

(a)振动能量响应图

(b)时域图

(c)相图图8 系统能量及位移响应图 (μ=0.1,f=0.3,β=1.0,γ2=0.05)Fig.8 Diagram of system energy and displacement response (μ=0.1,f=0.3,β=1.0,γ2=0.05)
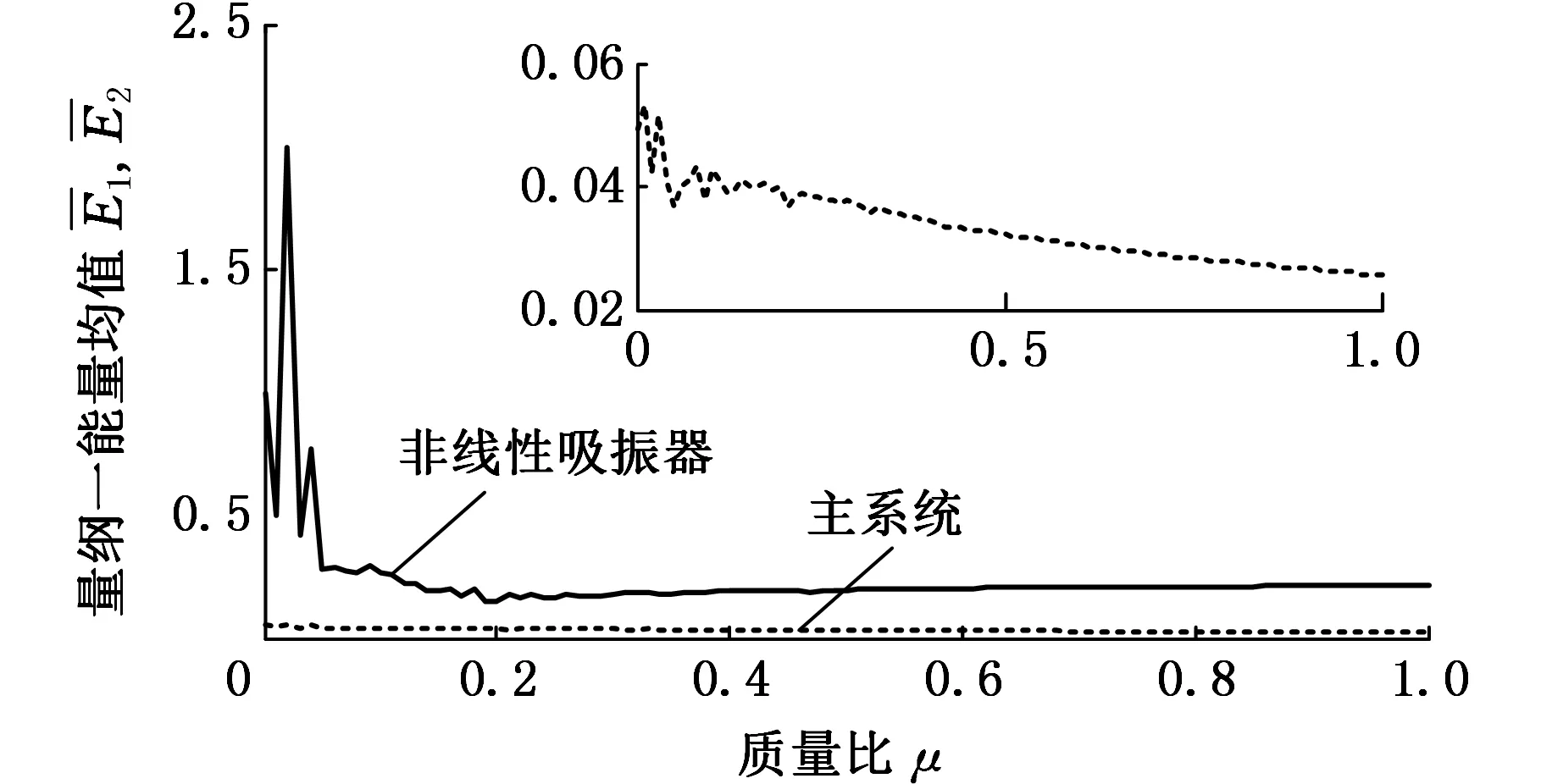
图9 能量变化曲线图Fig.9 Curve of energy change
阻尼对系统能量耗散起着关键作用,研究阻尼系数γ1对主系统振动能量的耗散和非线性吸振器振动能量的影响。通过对调谐频率比和质量比的仿真分析,选取f=0.3,β=1,μ=0.1,γ2=0.05,分析阻尼系数γ1对主系统和非线性吸振器的平均振动能量的影响,系统平均能量随参数γ1的变化如图9所示。从图9中可以看出,随着阻尼系数γ1的增大,主系统的平均能量出现了逐渐下降的趋势,但下降非常平缓。非线性吸振器出现了上升→最大值→下降→缓慢上升的总体趋势,γ1<0.05时,非线性吸振器平均振动能量出现了最大值,综合得出阻尼系数γ1的最优参数的区间为0.01~0.05。
取最佳阻尼系数区间0.01~0.05中的0.025为研究对象,来分析主系统和非线性吸振器振动能量的变化情况。图10是两系统的振动能量随时间的变化和时域图及相图。
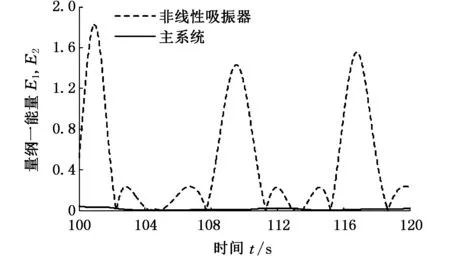
(a)振动能量响应图
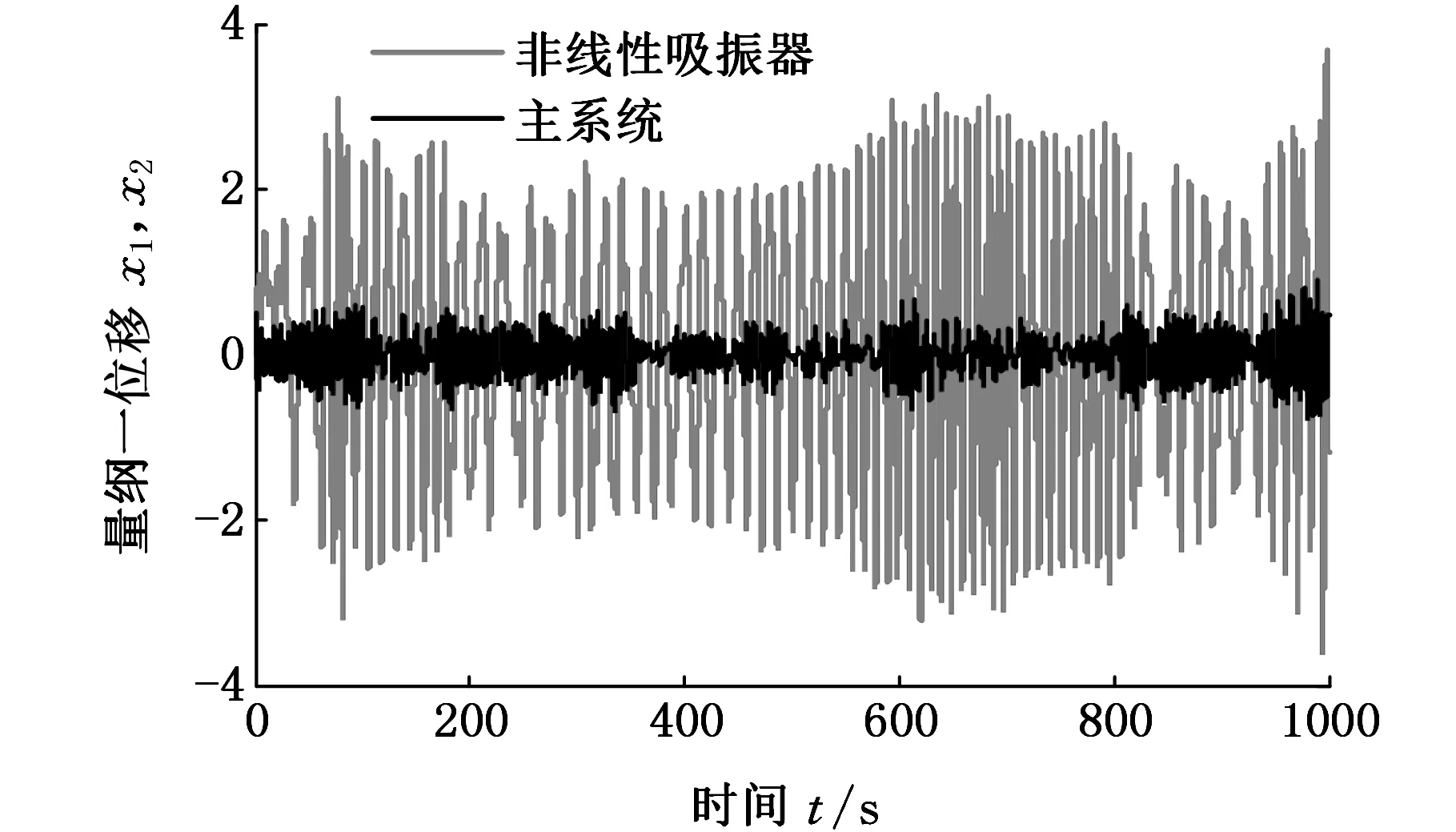
(b)时域图
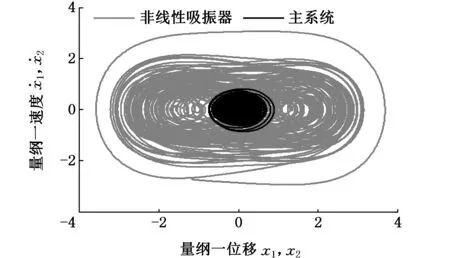
(c)相图图10 系统能量及位移响应图(γ1=0.025,f=0.3,β= 1.0,μ=0.3,γ2=0.05)Fig.10 Diagram of system energy and displacement response(γ1=0.025,f=0.3,β= 1.0,μ=0.3,γ2=0.05)
从图10a中可以看出,主系统振动能量比非线性吸振器的振动能量小得多,非线性吸振器吸收了大部分能量,实现了减振。从图10b、图10c中可看出,主系统在零平衡点附近做小幅运动的同时,非线性吸振器越过势垒,做大幅混沌运动,对比图6c、图8c可以看出,非线性吸振器越过势垒做大幅混沌运动的次数更多,更有利于发电。
综合比较图5、图7、图9可以发现,通过系统参数的逐渐优化,主系统的振动能量从0.05左右降到了0.04,非线性吸振器的最大振动能量逐渐加大,即0.31(图5)→0.77(图7)→2.0(图9),吸振器吸收了主系统的大部分能量,实现了最大程度的减振,更利于发电。
7 结论
(1)系统初值对主系统和非线性吸振器系统的振动能量均有较大影响。当系统初值中的吸振器位移、速度及主系统速度均取为零,主系统位移取为0.5时,主系统振动能量最小,吸振器的振动能量最大,且波动最小,吸振效果最佳。
(2)非线性吸振器对结构参数的变化较为敏感,结合初值仿真结果,通过逐步优化调谐频率比、质量比和阻尼系数,获得了使主系统振动能量最小、非线性吸振器振动能量最大的系统结构参数的最佳配置区间,即调谐频率比的最佳配置区间为0.2~0.4,质量比的最佳配置区间为0.02~0.15,阻尼系数的最佳配置区间为0.01~0.05。
[1]ZHANGYewei,ZHANGHao,HOUShuai,etal.VibrationSuppressionofCompositeLaminatedPlatewithNonlinearEnergySink[J].ActaAstronautica, 2016, 123:109-115.
[2]AL-SHUDEIFATMA.HighlyEfficientNonlinearEnergySink[J].NonlinearDynamics, 2014,76(4):1905-1920.
[3]STAROSVETSKYY,GENDELMANOV.DynamicsofaStronglyNonlinearVibrationAbsorberCoupledtoaHarmonicallyExcitedTwo-degree-of-freedomSystem[J].JournalofSound&Vibration, 2008, 312(1/2):234-256.
[4]AHMADABADIZN,KHADEMSE.NonlinearVibrationControlofaCantileverBeambyaNonlinearEnergySink[J].Mechanism&MachineTheory, 2012, 50:134-149.
[5]MADHAVCH,ALISF.HarvestingEnergyfromVibrationAbsorberunderRandomExcitations[J].IFACPapersonLine, 2016, 49(1):807-812.
[6] 张也弛, 孔宪仁, 张红亮. 非线性耦合振子间的靶能量传递研究:保守系统中的完全能量传递[J]. 振动与冲击, 2012, 31(1):150-155.ZHANGYechi,KONGXianren,ZHANGHongliang.StudyontheTargetEnergyTransferbetweentheNonlinearCoupledOscillators:theCompleteEnergyTransfer[J].VibrationandShockinaConservativeSystem, 2012, 31 (1):150-155.
[7] 张也弛, 孔宪仁. 非线性耦合振子间产生靶能量传递的初始条件[J]. 哈尔滨工业大学学报, 2012, 44(7):21-26.ZHANGYechi,KONGXianren.InitialConditionsforTargetEnergyTransferbetweentheNonlinearCoupledOscillators[J].JournalofHarbinInstituteofTechnology, 2012, 44(7):21-26.
[8] 熊怀, 孔宪仁, 刘源. 阻尼对耦合非线性能量阱系统影响研究[J]. 振动与冲击, 2015(11):116-121.
XIONGHuai,KONGXianren,LIUYuan.DampingEffectonCoupledNonlinearEnergyTrapSystem[J].JournalofVibrationandShock, 2015(11):116-121.
[9]DAQAQMF.TransductionofaBistableInductiveGeneratorDrivenbyWhiteandExponentiallyCorrelatedGaussianNoise[J].JournalofSound&Vibration, 2011, 330(11):2554-2564.
[10]TWETENDJ,MANNBP.ExperimentalInvestigationofColoredNoiseinStochasticResonanceofaBistableBeam[J].PhysicaD, 2014, 268:25-33.
[11]HARNERL,WANGKW.ProspectsforNonlinearEnergyHarvestingSystemsDesignedNeartheElasticStabilityLimitWhenDrivenbyColoredNoise[J].JournalofVibration&Acoustics, 2013, 136(2):325-325.
(编辑 张 洋)
Energy Transfer of Nonlinear Vibration Absorber under Colored Noise Excitation
LIU Lilan REN Bolin LI Shuchao ZHANG Xiaojing
School of Mechanical and Instrumental Engineering,Xi’an University of Technology,Xi’an,710048
Bistable oscillator was adopted as nonlinear vibration absorber herein. Mechanics model of main system with a nonlinear vibration absorber system was established. Nondimensional governing equation of the main system with the nonlinear vibration absorber system was obtained under colored noise excitation. Effect laws of structural parameters on vibration energy of the nonlinear vibration absorber and the main system were obtained by means of simulations, such as initial condition, tuning frequency ratio, mass ratio and damping coefficient. Optimal parameter configuration conditions of the nonlinear vibration absorber with maximum vibration energy of vibration absorber and main system with minimum vibration energy were obtained by means of gradual selection of the optimal parameters.
colored noise; nonlinear vibration absorber; mass ratio; tuning frequency ratio; parameter optimization
肖 虎,男,1983年生。南京航空航天大学机电学院博士研究生。主要研究方向为钛合金低温冷却加工。发表论文4篇。E-mail:hulimao-715@nuaa.edu.cn。李 亮,男,1971年生。南京航空航天大学机电学院教授。
2016-05-27
国家自然科学基金资助项目(11572243);陕西省自然科学基金资助项目(2016JM5020)
O322
10.3969/j.issn.1004-132X.2017.08.002

