基于格网坐标系的极区惯导误差分析
孙永侃, 张萍萍, 王海波, 张汉武
(海军大连舰艇学院, 辽宁大连 116018)
0 引言
传统惯导方法以地理北作为航向参考基准,以经纬度坐标表示位置[1],北极地区位于地球的最北端,经线迅速收敛,尤其在北极点,所有经线交叉汇聚,纬线也缩为一点[2],这就造成了在北极地区依据传统方法求解的导航信息精度无法满足极区船舶航行需求。
为解决传统惯导在极区存在的问题,1941年英国皇家空军中校K.C.Macl提出格网导航的概念,并对格网导航的应用进行了一系列的研究与探索[3-6]。2013年起国内文献开始出现针对格网导航的相关研究,周琪采用地心地固坐标系下的位置坐标替代传统经纬度坐标用于飞机定位[7]。之后周琪又提出通过游移坐标系和格网坐标系间的方向余弦矩阵,间接获取格网航向和格网速度[8]。周琪还针对高纬度地区地理经线收敛造成的定位难题,结合军用大飞机对全自主、高精度、长航时、全球范围导航能力的需要,提出了极区格网惯性/天文组合导航方案[9]。吴枫设计了格网导航坐标系下主子惯导信息的“速度+姿态”匹配传递对准算法。并进一步设计了格网系下雷达辅助捷联惯导的空中对准算法[10-11]。王荣颖指出在近极点区域,惯导系统会出现计算奇异值问题[12]。刘文超构建了椭球面栅格航向基准模型,并提出基于极球面投影的惯导高纬导航方法[13-14]。周本川提出基于惯性凝固格网坐标系的传递对准算法和载机火控系统极区导航算法[15]。
针对传统惯导方法在极区的使用缺陷,文中提出摒弃以经线作为航向参考基准,采用平行于本初子午线的平行线作为航向参考基准来解决因经线收敛引起的极区定向难题,并在此基础上构建格网坐标系作为极区定位空间坐标基准,以解决极区导航信息解算中面临的坐标基准的数学理论问题。
1 基于格网坐标系的极区导航方法
首先建立格网北。理论上格网北的方向可以是任意方向,为了换算方便,文中将格网北定义为平行于0°经线的方向,如图1所示。

图1 格网北示意图(虚线为格网北方向)
下面依据格网北建立如图2所示的格网坐标系,文中用字母G表示格网坐标系。定义载体所在点处平行于格林尼治子午面的平面为格网平面,载体所在的水平面为切平面,以两平面的交线作为格网坐标系的北向,格网坐标系的天向与地理坐标系的天向重合,格网坐标系的东向在切平面内与格网坐标系的北向垂直且构成右手直角坐标系,该坐标系即为格网坐标系。φ、λ分别表示载体所在地的纬度和经度。ex、ey、ez分别为M点在地球坐标系的3轴xe、ye、ze上的投影,eE、eN、eU分别为地理坐标系中的东北天,eGE、eGN、eGU分别为格网坐标系中的格网东、格网北与格网天,由对格网坐标系的定义可知格网天与地理天是重合的。定义σ为格网方位角,表示格网北与地理北的夹角。
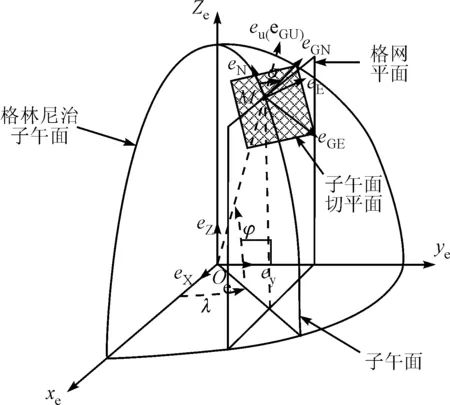
图2 格网坐标系
建立了格网坐标系作为空间坐标基准后,就可以对载体的导航信息进行相应的推算,具体推算过程文中不做详述。下面对该方法在极区应用中的误差进行详细分析以验证该方法在极区的有效性。
2 格网坐标系下导航信息误差模型的建立
通常惯导定位系统的误差来源多种多样,包括元器件误差、安装误差、初始条件误差、干扰误差、原理及方法误差、外信息误差等,此外惯导定位系统由各电气及机械与电子线路等分系统组成,各分系统也会各自受本身误差源的影响,从而影响系统误差。上述各误差源尽管来源不一样,但有些不同误差源对系统的影响是相似的,为了便于分析,文中在推导惯性导航系统的误差方程时,只引入初始条件误差和元器件误差等几种主要的误差源。
本节在推导误差方程时,规定符号“^”表示计算值,“~”表示测量值。
2.1 位置误差方程的解算
根据格网坐标系下的位置误差方程,位置的理想值由下式确定:
(1)
但是在实际系统中存在各种误差,所以实际的位置计算应由下述方程确定:
(2)
式中:
(3)
用式(2)减去式(1),并略去二阶小量,整理后得格网坐标系下的位置误差方程:
(4)
其中:
(5)
所以:
(6)
把式(6)代入式(4),整理后得格网坐标系下的位置误差方程:
(7)
2.2 速度误差方程的解算
根据格网坐标系下的速度微分方程式,当不考虑任何误差时,速度的理想值由下式确定:
(8)
但是在实际系统中存在各种误差,所以实际的速度计算应由下述方程确定:
(9)
式中:
在计算过程中,只考虑加速度计的零位偏置和测量系统噪声误差。
用式(9)减去式(8),忽略格网坐标系下重力加速度误差的影响,并略去二阶小量,整理得格网坐标系下的速度误差方程:
(10)
将式(10)整理后得格网坐标系下的速度误差方程:
(11)
2.3 姿态误差方程的解算
根据四元数定义可知,计算四元数的误差四元数为:

(12)
当只考虑陀螺仪常值漂移和测量系统噪声误差时,有:
(13)
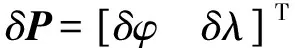

格网坐标系下的位置定位是以三维直角坐标形式描述,而非通常的经纬度。因此,要根据球面坐标系和直角坐标系的关系进行转换。
格网坐标系下的姿态误差方程为:
(14)
2.4 系统误差方程的解算
式(7)、式(11)和式(14)联立就构成了格网坐标系下的系统误差方程。
记状态变量为:
则系统误差方程可以写成:

(15)

(16)
式中:
为了便于分析,对误差模型进行简化,仅考虑系统在静基座条件下的情况,即:
VE=VN=VU=0
fE=fN=0
fU=-g
3 仿真与分析
在极区采用传统力学编排方案时,从60°N开始,姿态误差、速度误差、位置误差随纬度升高而缓慢增大;在纬度高于70°N以后,惯导误差随纬度升高而迅速增大;在纬度高于85°N以后,惯导误差随纬度升高而增大的程度尤为明显,纬度仅仅增加几度的情况下,航向角误差增大到约原来的两倍;在纬度高于89.87°N时,水平姿态误差和位置误差随纬度升高而迅速发散,惯导系统失去导航能力,惯导系统失去导航能力的最低纬度与载体速度有关,载体速度越大,失去导航能力的最低纬度越低。
为验证以格网坐标系作为空间坐标基准的定位精度,分析载体静止时系统的性能,用MATLAB对其静基座条件下的系统误差方程进行仿真。
以舰艇运动特性为例,仿真参数设置如下:载体静止,所在点为[80°N,120°E];格网坐标系下航向为20°,纵摇角为0°,横摇角为1°;数学平台失准角分别为[1′,1′,2′];载体的速度误差为δVE=δVN=δVU=0.05 m/s;在地球坐标系下的位置误差为δx=δy=δz=1 m;陀螺仪的常值漂移为εx=εy=εz=0.05°/h;加速度计的零位偏置为x=y=z=0.000 05g;陀螺仪的测量系统噪声和加速度计的测量系统噪声用高斯白噪声随机函数表示;仿真时间为24 h。仿真结果如图3~图10所示。

图3 φE的仿真图
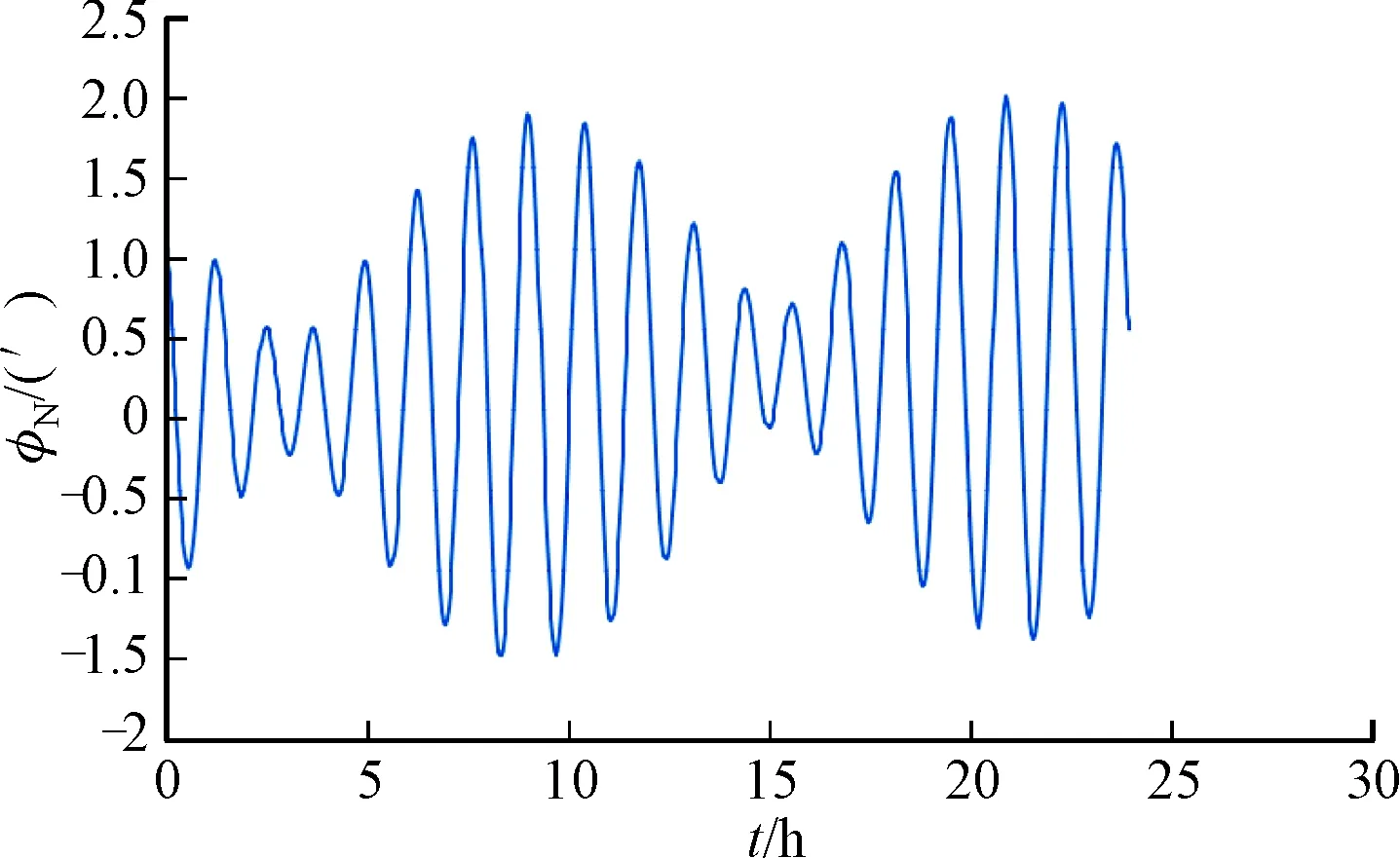
图4 φN的仿真图
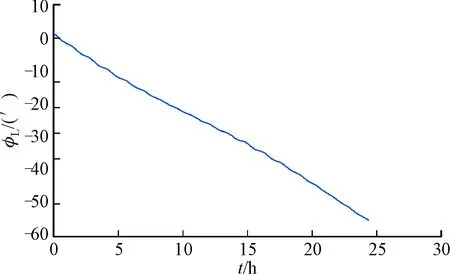
图5 φU的仿真图

图6 δVE的仿真图

图7 δVN的仿真图

图8 δVU的仿真图
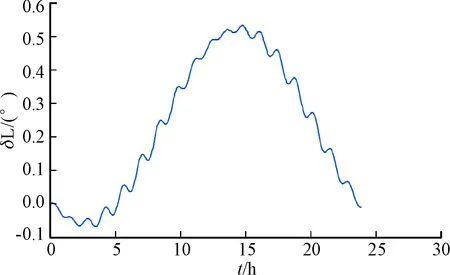
图9 δL的仿真图

图10 δλ的仿真图
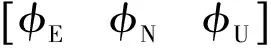
由格网坐标系下的仿真曲线和误差统计数据与传统力学编排方案的对比可以发现:在极区以格网坐标系作为空间坐标基准进行惯导信息的解算,可以有效的解决极区因经线快速收敛所引起的定位误差增大问题,能够满足极区定位精度需求。同时,由仿真曲线可以看出:载体的速度和在地球坐标系下的位置误差都呈现发散特性。因此为保证载体在极区的长航时高精度定位需求,可以利用组合技术抑制格网坐标系定位系统的误差发散。
4 结论
文中为了解决极区导航参数解算中面临的坐标基准的数学理论问题,提出采用格网坐标系作为空间坐标基准进行导航信息的推算,根据误差源对系统的影响,推导出在格网坐标系下的导航误差方程,并进行了仿真试验。仿真结果表明在极区采用格网坐标系作为空间坐标基准用来解算导航参数能够提供高精度的导航信息。
参考文献:
[1] 秦永元. 惯性导航 [M]. 北京: 科学出版社, 2006: 203-231.
[2] 王有隆. 北极地区飞行中的通信与导航特性 [J]. 航空维修与工程, 2006(1): 46-48.
[3] DOWDLE John, FLUECKIGER Karl. Submeter navigation grid system concept [C]// Position Location and Navigation Symposium, IEEE 2000. [S.l.]: IEEE, 2000: 270-276.
[4] STEWART Robert E. Submarine navigation under the north pole [C]∥ AIAA. AIAA Guidance, Navigation, and Control Conference and Exhibit. [S.l.]: AIAA, 2001: 1-6.
[5] SMUEL Herrick. Grid Navigation[J]. Geographic Review, 1944, 34(3): 135-147.
[6] KENDALL E C. Gyro/Grid Navigation[J]. Journal of Navigation, 1956, 9(4);429-435.
[7] 周琪, 秦永元, 付强文, 等. 极区飞行格网惯性导航算法原理 [J]. 西北工业大学学报, 2013, 31(2): 210-217.
[8] 周琪, 岳亚洲, 张晓冬, 等. 极区飞行间接格网惯性导航算法 [J]. 中国惯性技术学报, 2014, 22(1): 18-22.
[9] 周琪, 秦永元, 严恭敏, 等. 大飞机极区惯性/天文组合导航算法 [J]. 系统工程与电子技术, 2013, 35(12): 2559-2565.
[10] 吴枫, 秦永元, 周琪. 机载武器极区传递对准算法 [J]. 中国惯性技术学报, 2013, 21(2): 141-146.
[11] 吴枫, 秦永元, 张金亮. 极区内基于雷达辅助的SINS空中对准算法 [J]. 西北工业大学学报, 2014, 32(1): 131-136.
[12] 王荣颖, 刘文超, 卞鸿巍, 等. 惯导系统极区导航性能仿真分析 [J]. 海军工程大学学报, 2014, 26(3): 75-79.
[13] 刘文超, 卞鸿巍, 王荣颖, 等. 惯性导航系统极区导航参数解算方法 [J]. 上海交通大学学报, 2014, 48(4): 538-543.
[14] 刘文超, 卞鸿巍, 王荣颖, 等. 基于极球面投影的惯导高纬导航方法 [J]. 华中科技大学学报(自然科学版), 2014, 42(8): 27-32.
[15] 周本川, 鲁浩. 空空导弹捷联惯导系统极区导航算法设计 [J]. 航空兵器, 2013(6): 9-11.

