塑性垮塌载荷在导弹结构强度分析中的应用
许 斌, 邵 庆, 刘 广, 唐晓峰, 武秋生
(上海机电工程研究所, 上海 201109)
0 引言
结构是导弹的重要组成部分。在导弹结构设计过程中,首先受到关注的便是结构在载荷作用下是否发生破坏或失效。长期以来,人们采用极限应力法[1]开展导弹结构强度分析与评价,即考虑在最大载荷工况,按静力载荷(考虑一定的安全系数)计算得到的最大应力点控制在材料强度极限以内[2-3]。并且根据材料的强度极限与结构在载荷作用下的最大应力进行对比,用于计算剩余强度系数。
人们一般利用通用有限元软件开展工程结构分析。这些软件基于有限元位移法开发,应力结果作为二次量,其精度有所下降;并且最大应力所在部位有限元网格划分对其结果有很大的影响。因此,采用应力进行结构强度评价,结果的准确度在很大程度上依赖于分析人员的经验。另一方面,铝合金、钛合金、合金钢等弹塑性金属材料广泛应用于导弹结构[4]。而弹塑性材料具有非线性本构关系。在结构最大应力超过材料屈服极限之后,最大应力的增长与外载荷的增长一般不是线性关系。这时,应力已经不再是主要的特征量,采用应力进行评价并不合适。实际上,在压力容器设计领域,已经在推广使用极限载荷分析法、弹塑性分析法[5],并采用以极限载荷与塑性垮塌载荷为控制界限的塑性失效准则。
对于采用弹塑性材料的导弹结构的强度分析,弹塑性分析法也更为适用。文中首先介绍了极限分析与弹塑性分析方法,以及确定塑性垮塌载荷的准则;并应用该方法完成了导弹折叠翼的静力分析;通过与试验结果对比,验证了分析的准确性。对比传统的极限应力法,跨塌载荷方法在弹塑性材料结构强度分析中更为合理。
1 极限分析与弹塑性分析
对于弹塑性材料制成的结构,在加载过程中随着外载荷的增加,应力高的地方首先发生屈服。若载荷持续增加,塑性区域范围将不断增大,结构最终进入总体塑性流动状态。
极限分析是塑性力学理论中很重要的一部分内容。极限分析假设材料为理想塑性,并且认为结构处于小变形状态,研究塑性极限状态下的结构特性。理想塑性材料进入塑性后应力始终保持为屈服极限,有理想弹塑性和理想刚塑性两类模型(如图1(a)、(b)所示)。前者常用于有限元分析,后者用于求解析解,都是真实材料的简化模型。用极限分析方法求得的结构所能承受的最大载荷,称为极限载荷。在该载荷作用下,结构的变形将无限制的增大,从而失去承载能力,这种状态称为结构的塑性极限状态。
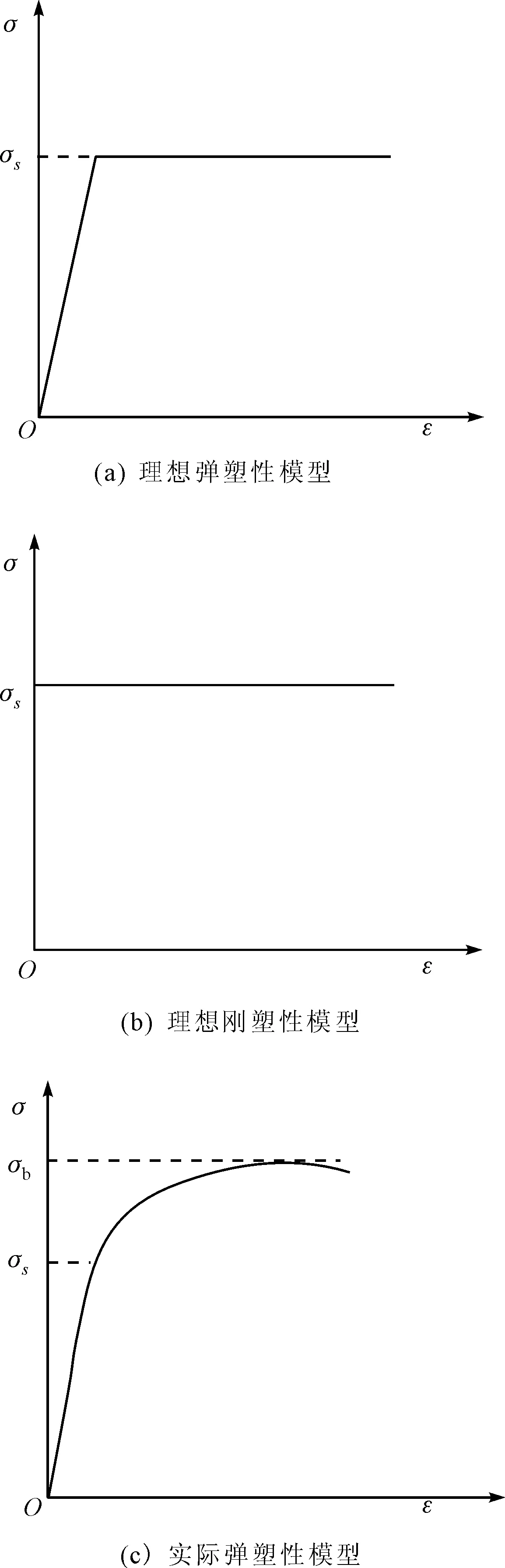
图1 材料本构模型
需要指出的是,极限载荷的定义是在采用理想弹塑性材料模型的基础之上,而且只考虑小变形的情况。但实际中真实材料一般都具有一定的应变硬化效应和几何强化或弱化效应,因此按这种方法分析得到的极限载荷并不代表真实的破坏载荷。如桑芝富等[6]对正接管内压容器计算得到的塑性极限载荷平均值为3.26 MPa,而物理试验得到的破裂载荷为7.40 MPa,两者相差了55.95%。
尽管塑性极限载荷不是真正意义上的极限载荷,但其仍然具有相当重要的工程应用价值。这是因为工程结构设计通常是基于安全裕度的设计思想,塑性极限载荷分析能够很好地用于确定这样的限度。美国压力容器设计规范ASME-Ⅷ-2[7]中规定,压力容器设计的许用载荷为结构塑性极限载荷的2/3。
为了通过试验确定塑性极限载荷,研究人员提出了许多种准则,包括两倍弹性斜率、准则双切线交点准则等[8]。如两倍弹性斜率准则将载荷-位移曲线与两倍弹性斜率线的交点处所对应的载荷值定义为极限载荷。利用有限元数值方法确定极限载荷,也需要选择合适的准则,原则上针对试验提出的确定极限载荷的方法都可以适用。在文献[5]中,陆明万等介绍了一种新的方法:绘制载荷-最大位移曲线。当该曲线已经算到趋于水平(如该加载步的曲线斜率已小于弹性斜率的百分之一)的阶段,达到了极限载荷。这种方法与美国压力容器设计规范中所定义的极限载荷相一致:“极限载荷是使总体结构不稳定的载荷,这表现为对小的载荷增量求解不收敛(即求解发散)”。
与极限分析法相比,弹塑性分析法更加符合实际情况。随着有限元分析技术应用的深入,弹塑性分析法逐步受到人们的关注,美国压力容器设计规范也对此方法进行推荐。弹塑性分析采用实际弹塑性关系(如图1(c)所示)建立材料的本构模型,并且考虑非线性的应变-位移关系,在已变形的结构形状基础上建立平衡关系。在弹塑性分析中,导致总体结构不稳定的载荷称为塑性垮塌载荷。极限载荷实际上是采用弹性-理想塑性材料和线性小变形理论假设时的塑性垮塌载荷。而确定塑性极限载荷的方法也可以用于确定塑性垮塌载荷。
2 折叠翼强度分析
2.1 折叠翼结构及材料
翼面是导弹上的常见升力面。图2是一个采用根部折叠的翼面,翼面可以绕转轴进行旋转,旋转到位后,通过前、后锁销将翼面与接头锁紧。折叠翼主要组件的材料力学性能如表1所示。在飞行过程中,折叠翼承受的最大载荷为8 725.5 N,作用力压心见图2。
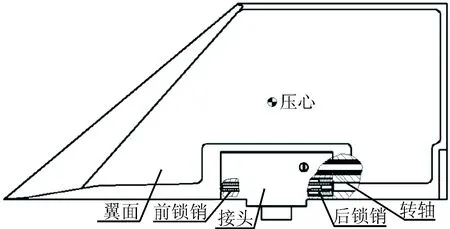
图2 折叠翼模型示意图
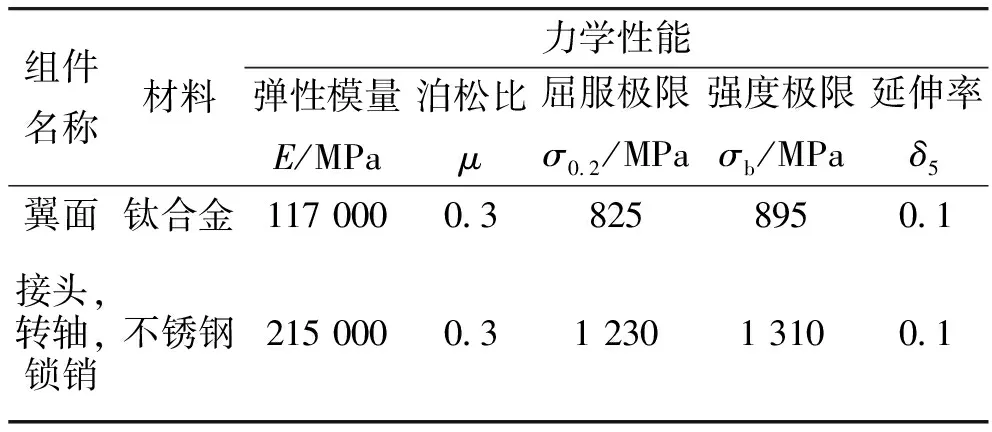
表1 折叠翼组件材料的力学性能
2.2 有限元弹塑性分析
首先对折叠翼各组件进行网格划分。锁销与转轴全部采用六面体网格;翼面、转头因结构相对复杂,在它们与锁销、转轴接触部位等区域采用六面体网格,其余采用四面体网格,如图3所示。对于材料特性,由于表1中给出的是强度极限、延伸率的名义值,需按式(1)、式(2)进行计算,得到材料的真实应力应变关系。
σt=σe(1+εe)
(1)
εt=ln(1+εe)
(2)
式中:σt与εt分别为真实应力与真实应变,σe与εe分别为名义应力与名义应变。按该式计算,钛合金与不锈钢的真实强度极限分别为985 MPa与1441 MPa,对应的真实应变则均为0.095。
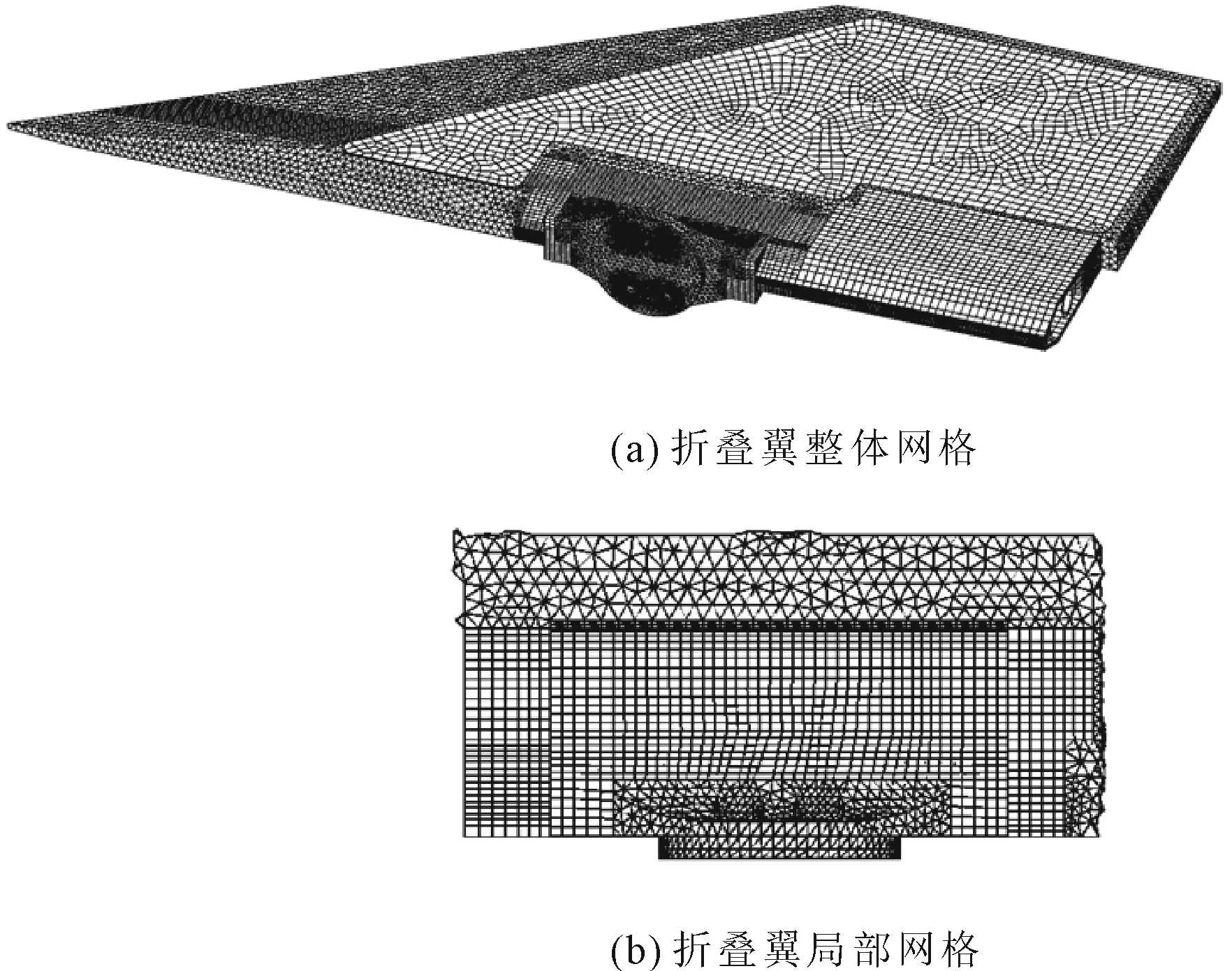
图3 折叠翼网格图示
固定折叠翼接头根部的3个平动自由度。在翼面、接头与转轴、锁销等组件之间,在接触部位定义接触约束。为了计算垮塌载荷,将使用载荷放大3倍,即采用26 176.5 N进行加载。将作用载荷按照压心等效原则,分为7个载荷,以反映分布式气动载荷的特点。在进行前述有限元分析的前处理工作之后,进行考虑几何非线性的弹塑性分析。
2.3 计算结果讨论
弹塑性分析在载荷施加到70.8%,即2.12倍使用载荷的时候,由于收敛困难,计算停止。其中在加载到50%,即1.5倍使用载荷的时候,折叠翼翼面、转轴的应力分布如图4所示。从图中可见,翼面与转轴接触部位有相当大的区域已经达到材料的强度极限,如果按照应力评价方法,翼面能够承受的载荷应该是不大于1.5倍的使用载荷,如果对比1.5倍的安全系数要求,该翼面的剩余强度系数达不到1,不能满足设计要求。
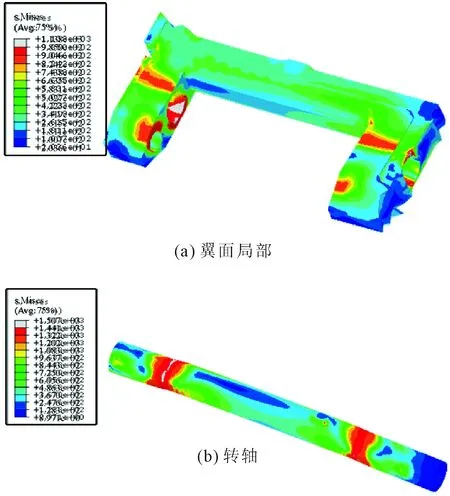
图4 应力分布图(1.5倍使用载荷)
按照塑性垮塌载荷进行评价,若按“有限元计算在小载荷步时不能收敛”的准则确定塑性垮塌载荷,则2.12倍使用载荷,即18 498.1 N为其塑性垮塌载荷。需要指出的是,折叠翼计算模型中设置了接触关系,其带来的非线性也会导致计算难于收敛,因此,需进一步结合结构的应力及变形情况进行判断。在2.1倍使用载荷时翼面的应力分布图如图5所示,从图中可见,转轴已经严重变形,在严重变形区域的应力已整体性达到强度极限。因此基本可以判断该载荷即是或已非常接近于按该准则定义的塑性垮塌载荷。
翼面上变形最大点的位移随载荷变化曲线如图6所示。由于计算时并未考虑材料在应力达到强度极限后失效,可能导致按前述方法确定的垮塌载荷大于真实结构的承载能力。另一方面,在2.12倍使用载荷时,翼面的变形已经很大,对翼面的气动性能产生较大的影响,这是不希望出现的。因此,选择按“两倍弹性斜率准则”确定塑性垮塌载荷。绘制两倍弹性斜率线,与载荷-位移曲线的交点在1.73倍使用载荷处,即载荷为15 095.1 N。对比1.5倍的安全系数要求,该翼面的剩余强度系数为1.15,翼面强度满足设计要求。
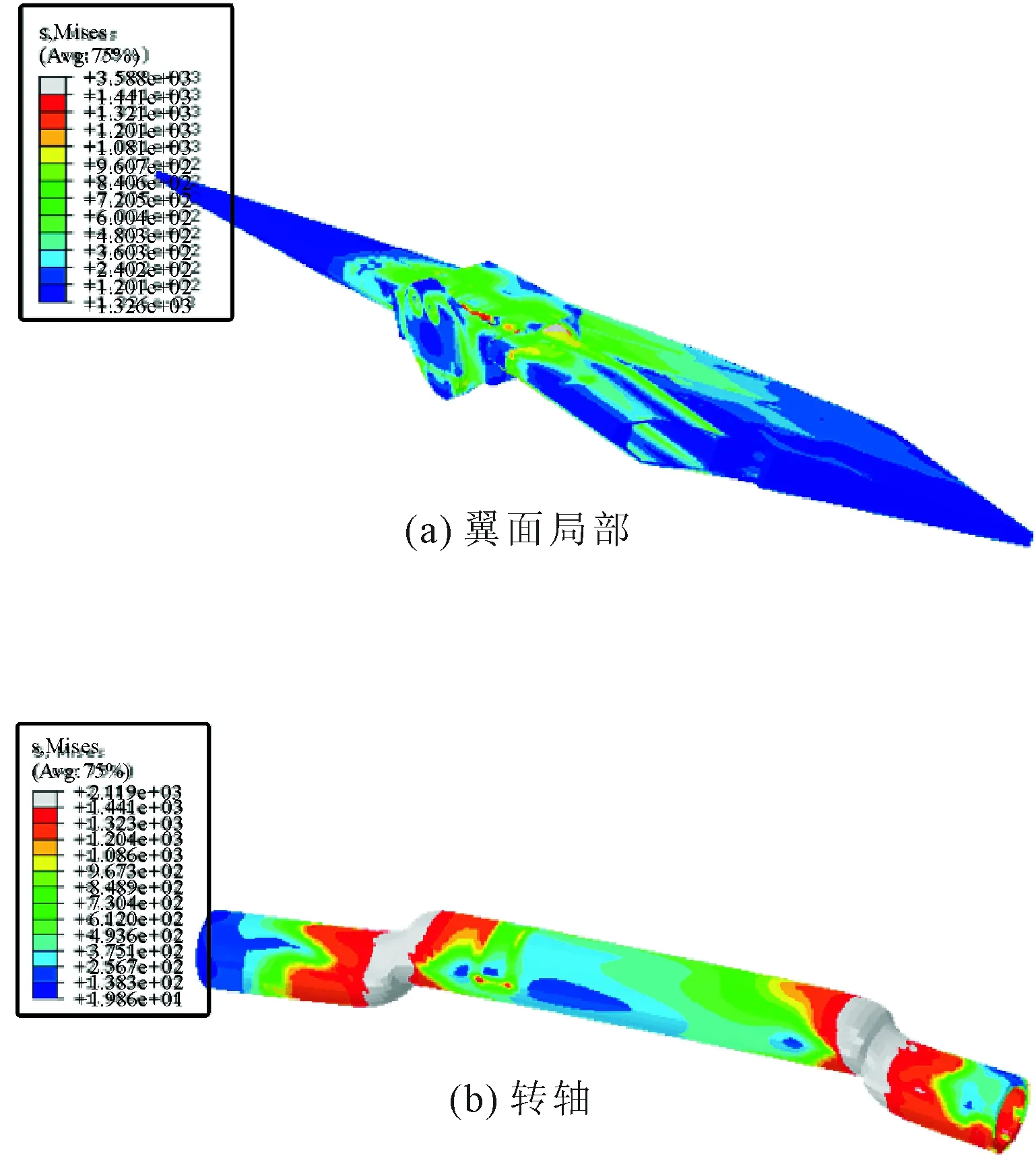
图5 应力分布图(2.1倍使用载荷)
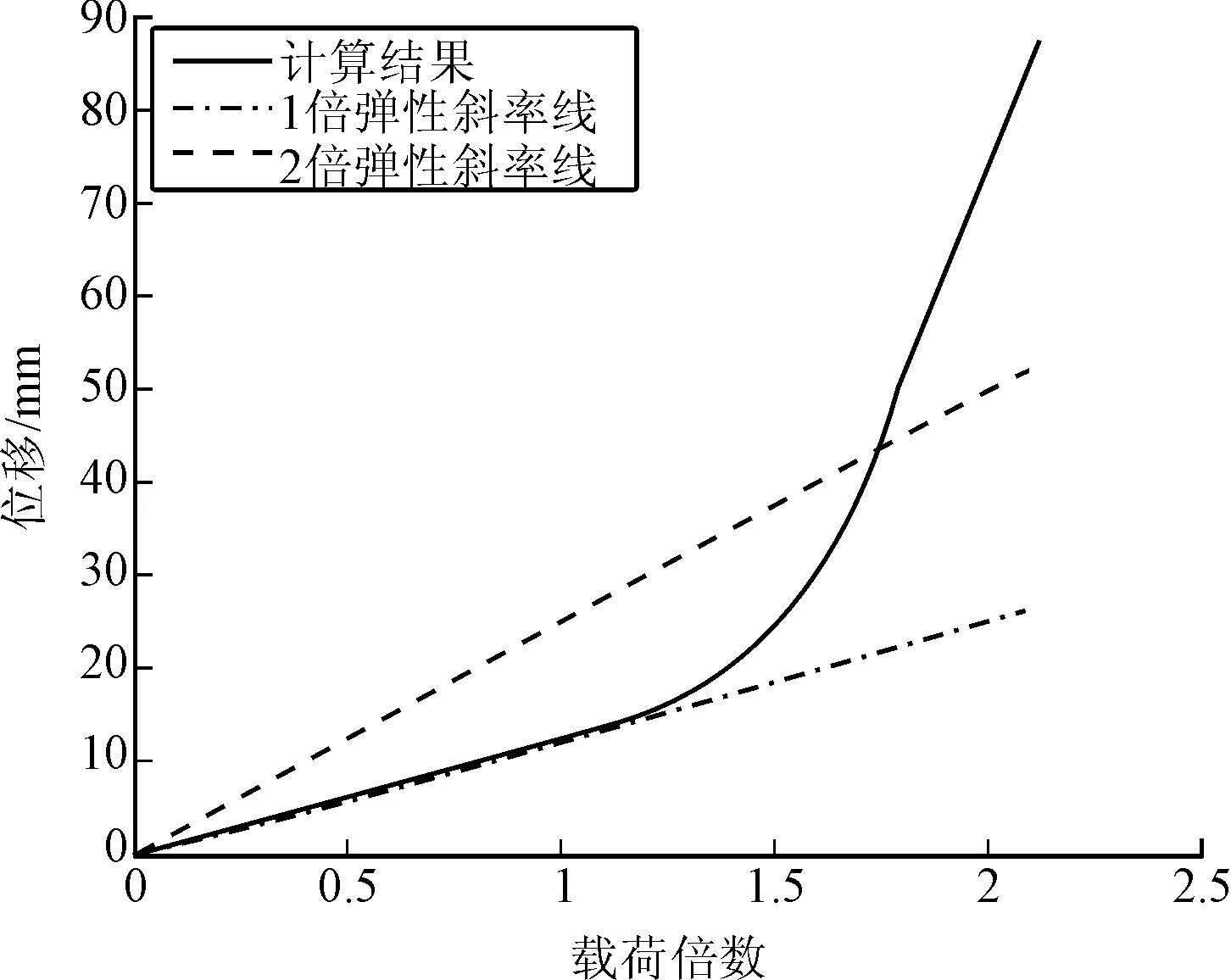
图6 位移-载荷曲线(有限元分析)
3 分析结果的试验验证
对该折叠翼面进行静力试验,试验件支撑与加载方式与前述计算模型相同。试验得到的最大变形点位移见表2(表中设计载荷为使用载荷的1.5倍)。试验加载到131%设计载荷时折叠翼破坏,照片见图7。因此,1.31倍设计载荷,即1.965倍使用载荷为试件的破坏载荷。对比有限元计算在2.12倍使用载荷时无法收敛,计算结果比试验结果大7.89%。
按“两倍弹性斜率准则”确定试验件的塑性垮塌载荷。绘制试验得到的位移随载荷变化曲线及其两倍弹性斜率线,如图8所示。可知两倍弹性斜率线与载荷-位移曲线的交点在1.76倍使用载荷处。对比1.5倍的安全系数要求,该翼面的剩余强度系数为1.17,翼面强度满足设计要求。计算结果与试验结果相对比,其偏差为-1.7%通过对比,计算结果具有较高的准确性。结合试验情况与有限元计算结果,可见采用塑性垮塌载荷计算得到的折叠翼剩余强度系数更加准确。
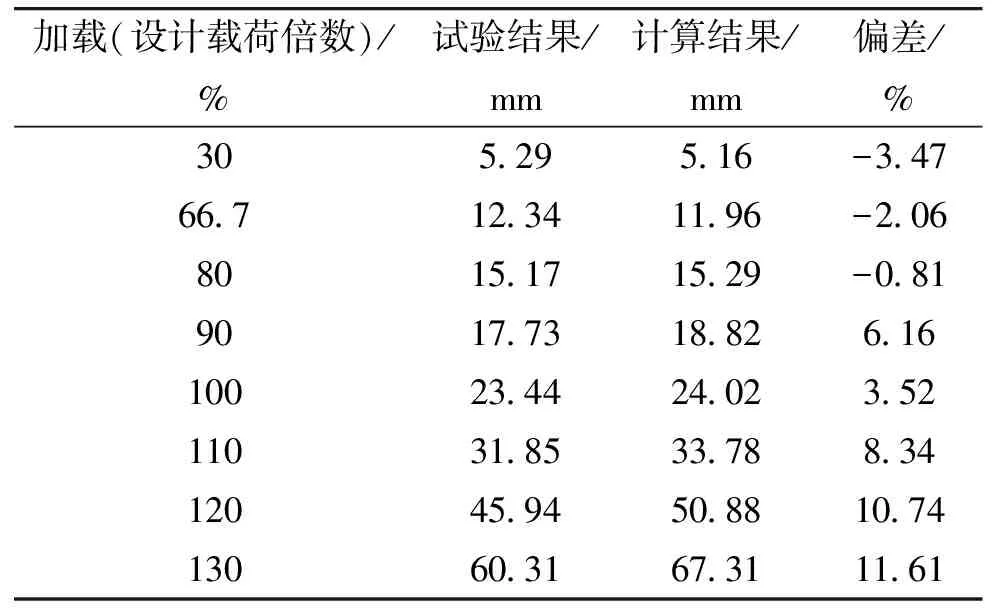
表2 折叠翼静力试验结果与计算结果对比

图7 静力试验后的试件
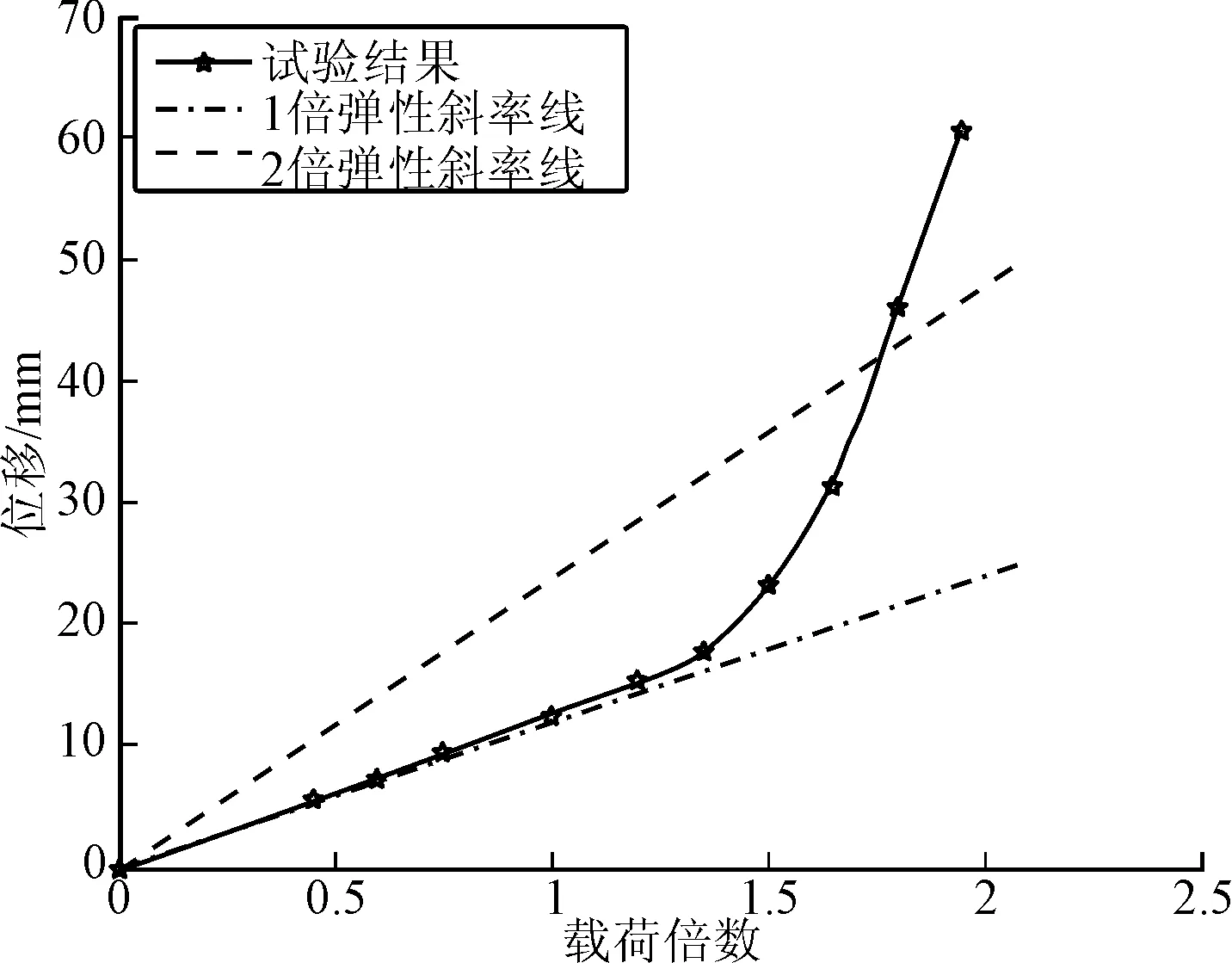
图8 位移-载荷曲线(静力试验分析)
4 结论
现代导弹结构广泛使用弹塑性材料。对于这类结构,目前广泛采用的应力评价方法不能准确揭示结构的承载能力。
采用弹塑性有限元分析方法对导弹折叠翼面进行强度分析,静力试验验证了分析结果的准确性。对比采用塑性垮塌载荷方法与最大应力方法对折叠翼面的承载能力的评价结果,表明采用塑性垮塌载荷更加准确。在评估导弹折叠翼面的承载能力时,用“两倍弹性斜率准则”比“有限元计算在小载荷步时不能收敛准则”确定塑性垮塌载荷更为合适。
在导弹结构设计中,可以推广使用极限载荷分析法、弹塑性分析法,并采用以极限载荷与塑性垮塌载荷为控制界限的塑性失效准则。但在确定极限载荷或垮塌载荷时,仍需进一步结合具体结构的失效形式,结合其应力分布、变形情况,选用合适的塑性垮塌载荷确定准则。
参考文献:
[1] 李金瀛. 工程强度设计规范中的塑性准则 [J]. 水利电力机械, 1994(6): 24-25.
[2] 王晓慧, 樊思思, 周健鸥, 等. 基于混合变量的导弹舱段径向连接结构综合优化设计 [J]. 固体火箭技术, 2015, 38(6): 857-859.
[3] 郭颜红, 门们. 导弹壳体翼面安装座连接结构分析 [J]. 航空制造技术, 2008(4): 76-79.
[4] 王永寿. 导弹结构材料的应用预测 [J]. 飞航导弹, 1997(12): 48-50.
[5] 陆明万, 寿比南, 杨国义. 压力容器分析设计的塑性分析方法 [J]. 压力容器, 2011, 28(1): 33-39.
[6] SANG Z F, XUE L P, LIN Y J, et al. Limit and burst pressure for a cylindrical shell intersection with intermediate diameter [J]. International Journal of Pressure Vessels and Piping, 2002, 79(5): 341-349.
[7] ASME Boiler Pressure Vessel Committee on Pressure Vessels. ASME BPVC-VIII-2-2007 alternate rules [Z]. New York: The American Society of Mechanical Engineers, 2007.
[8] 周小玲. 半球封头圆柱壳结构的塑性极限载荷分析 [D]. 重庆: 重庆交通大学, 2015.

