离散小波改进算法在机动车辆换挡信号降噪中的应用*

高鲜萍，成英，王祥鑫

（天津职业技术师范大学汽车与交通学院，天津300222）

离散小波改进算法在机动车辆换挡信号降噪中的应用*

高鲜萍，成英，王祥鑫

（天津职业技术师范大学汽车与交通学院，天津300222）

针对机动车辆换挡信号中存在大量强电磁及环境振动噪声的问题，同时考虑到实时性和硬件实现性能的需求，基于最小带宽离散小波算法，提出了简化的、适用于工程实现的小波分解层数确定方法；然后利用初始阈值对各层小波系数进行分类，利用各层中各类系数均值差的模及均方差为依据，设计了各层阈值的自适应迭代确定算法，同时改进了阈值的量化函数。仿真对比试验和应用测试结果表明，该算法具有较好的降噪效果，适用于机动车辆的相关信号检测与降噪。

换挡信号，最小带宽离散小波，小波降噪，自适应阈值

0 引言

车速信号与变速箱节气门开度合理匹配形成机动车辆的升降挡控制信号，然而在实际行驶测试中发现，车体内部强电磁及环境振动的影响使得机动车辆换挡信号的采集量常伴有大量噪声，使换挡信号失真进而影响车辆换挡控制效果。因此，适当且有效的降噪算法对机车控制性能的提升至关重要。车载振动环境下的噪声源复杂且信号具有非平稳特性，如短时傅里叶变换［1］、低通滤波［2］、最优估计［3］等常规方法多适用于平稳信号，难以将噪声从信息中分离，使降噪效果受限。故目前在非平稳信号分析等方面多采用非线性小波阈值降噪算法来获得更好的降噪性能［4-5］，虽然连续小波变换算法在理论上可利用信号与噪声的小波系数在各尺度上具有不同性质的特性进行有效信号的提取，但受到计算量、算法复杂度等因素影响，使得其在工程上应用效果受限，因此，为保证系统实时性和硬件实现性能，在机车挡位信号检测的实际应用中对小波阈值降噪算法进行简化和改进具有实际的工程意义。

经实验和测试发现，小波分解层数合理性和阈值选取原则在工程上对信号降噪效果和重构精度影响很大［6］。小波分解层数过少会造成降噪效果不理想、分解层数过多则会增大运算量，造成有效信息丢失，故不同信噪比环境下对于特定信号都存在1个降噪效果最佳或接近最佳的分解层数。文献［7］利用小波系数奇异谱分析进行最优分解层数的自适应选择，与经典小波降噪算法进行对比表明，文中算法有效提高了实用性能；文献［8］提出了基于白化检验的小波变换最优分解层数自适应确定算法。以上算法虽在理论上有一定效果但却额外增加了运算量，算法冗余程度过高。而在阈值选取方面，软、硬阈值法虽得到了广泛地应用但仍存在一些不足［9］，经过硬阈值法处理后的小波系数存在偏差，其重构的信号将出现振荡、伪吉布斯等视觉失真；软阈值法则会在小波系数高于阈值时，存在一定的系数恒定差，进而造成信号的重构失真。针对此问题，国内外许多学者提出了一些解决方案和改进算法，如文献［10］改进了阈值函数，并与自适应阈值相结合，实现了对有固定频谱噪声的抑制；文献［11］设计了新的阈值函数量化法，并与软、硬阈值去噪方法进行对比，提高了汽车轮速信号的去噪效果；文献［12］以小波系数方差和噪声方差为依据提出了一种自适应阈值优化算法，但仅在信噪比较小的情况下具有较稳定的降噪效果。

鉴于此，本文基于最小带宽离散小波算法，提出了简化的、适用于工程实现的小波分解层数确定方法；然后利用初始阈值对各层小波系数进行分类，利用各层中各类系数均值差的模及均方差为依据，设计了各层阈值的自适应迭代确定算法，同时改进了阈值的量化函数；并将该改进算法应用于机车的挡位信号检测与降噪。仿真对比试验和应用测试结果表明，该算法具有较好的降噪效果，且可很大程度地缩短运算时间。该算法在滤除噪声的同时能较好体现信号细节信息，适合于对实时性和准确性要求较高的机车相关信号检测当中。

1 离散小波阈值降噪原理

基于离散小波的阈值降噪是按照一定的预设阈值量化信号小波系数，然后用量化后的系数进行信号重构以实现降噪和滤波的作用。为提高硬件系统解算速率，本文采用最小带宽离散小波算法实现信号的快速分解，将采样得到换挡信号分解成多个频率带的小波系数。设挡位信号经抽样后的离散含噪信号为f（n），并设伸缩因子a=a0l、平移因子b= ka0lb0，令a0=2、b0=1，则其对应母小波函数为

则信号f（n）的二进离散小波变换为

其正交小波分解系数为

式中，l为分解层数；N为离散采样点数；cl，k为尺度系数，dl，k为小波分解系数；h、g分别为低通和高通滤波器。

在分解得到离散采样信号的小波系数后，需对各系数进行阈值量化处理，根据最低层小波包分解系数和经过量化处理的系数，进行小波重构。小波重构过程是分解过程的逆运算，其重构公式为

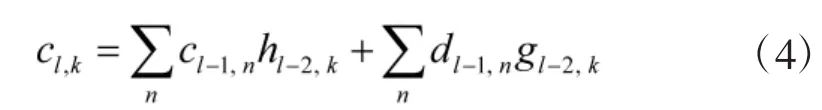
由以上所述可知，换挡控制中的噪声信号多包含在具有较高频率的细节中，对换挡信号进行小波分解时，可利用门限阈值等形式对所分解的小波形式进行处理，然后对换挡信号进行小波重构即可达到对信号降噪的目的。因此，在对含噪换挡信号进行小波分解的过程中，当分解到最佳层数后，有用信号的小波系数将大于噪声的小波系数，这样，通过阈值收缩方式即可实现对含噪信号的去噪处理。

2 分解层数的最优确定算法

离散小波分解层数对于信号降噪效果的影响很大，是决定小波降噪性能的关键之一。分解层数过多会增大运算量，同时造成降噪后的信噪比下降；过少则会导致只有高频系数能进行阈值处理，而低频段的噪声则无法去除。另外，根据信号特性与人为经验决定的固定的分解层数，通常难以保证机车换挡信号在不同信噪比下均能获得最优的降噪效果［14］。

机车换挡信号降噪的目的是提出采样信号特征，故分解得到的小波系数必须可反映挡位信号的最小频率成分，因此，出于工程应用需求的考虑，本文提出根据挡位信号的最小带宽确定最优分解层数的简化算法。

通常情况下，较窄的频带宽度有助于减少噪声对信号分解精度的影响，最小频率带宽度决定于挡位信号特性以及采样量Nsamp。而采样量Nsamp则由采样频率fsamp和采样窗口宽度Tw确定，

为确保分解精度，频带的宽度Wb必须小于所需要信号频率分辨率［15］，其最小频带宽度Wb_min的计算公式如式（6）所示

式中，m=p+q。

在挡位信号采样量及最小分解带宽确定的情况下，分解层数ln由式（7）所示的不等式进行确定，即

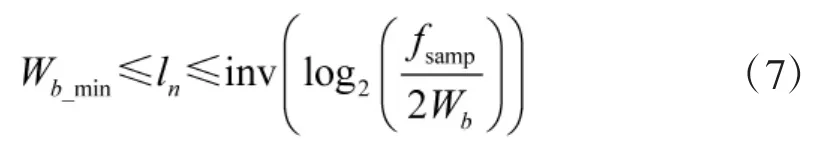
其中，inv（*）为取整函数。

3 自适应分层阈值降噪改进算法

3.1 分层阈值自适应确定算法

目前，无偏似然估计原则、固定阈值原则、启发式阈值原则、极值阈值原则和惩罚函数等是小波阈值降噪中阈值确定常采用的策略原则，而以上策略多是参数化或有约束最优化问题，通过转化并求解极值来确定全局最优阈值。然而，根据文献［16］的相关研究表明，信号与噪声具有相反的奇异性，随着小波分解尺度的增大，两者幅度和稠密度的变化趋势不同，故在不同分解层，应根据信号的特点选择不同的阈值进行降噪。因此，采用常规原则确定统一的全局阈值显然具有一定的局限性，在此利用小波系数均值差平方与组内系数标准差作为判别依据，提出一种阈值的分层自适应迭代确定方法。

设第li层小波分解变换后的小波系数序列为，并假设阈值已知，则以为界，将序列M分成两组，即

定义序列M1、M2的均值为μ1、μ2，标准差为s1、s2。为达到良好的降噪效果，应将同一层内的两组小波系数尽量分开，但各组内部尽量密集，即希望两组序列的均值差尽量大，而各组标准差尽量小，并以两组均值差的模与序列总标准差和的比值作为准则函数。

为进行迭代计算，首先通过折中的方式选取某层li的初始阈值，即

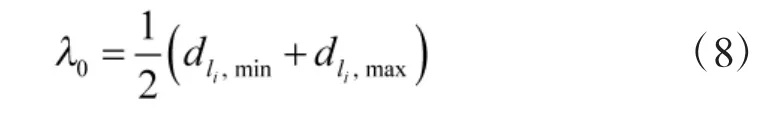
再求各组系数序列的均值和标准差，

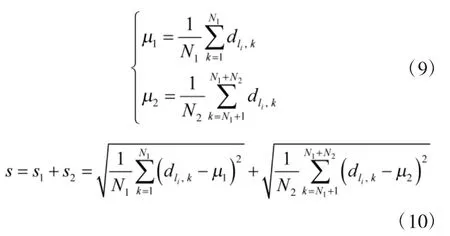
之后定义准则函数为

3.2 阈值量化函数改进

在确定了各层阈值之后，需利用所选阈值将对应层的部分小波系数进行量化重置。目前采用较多的两种策略为硬阈值和软阈值算法，硬阈值算法会保留绝对值大于阈值的小波系数，而将其他小波系数则作为噪声置0，该算法重构的信号光滑性较差且可能会丢失部分有用信息；软阈值算法则将符合不等式条件的小波系数做降幅收缩，其他小波系数置0，该算法整体连续性好，但其重置后的小波系数存在恒定差，进而影响到信号重构的逼真度，造成边缘的模糊失真。为克服以上所述不足，此处结合以上两种策略，提出一种阈值量化的改进函数，即

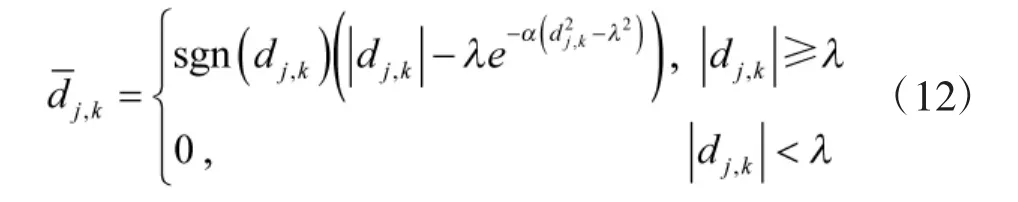
其中，sgn（*）为符号函数，∀α＞0为调节参数。由式（12）可看出，随着|dj，k|的增大将渐进逼近dj，k。该函数兼顾了软、硬阈值函数的优点，对层内小波系数的量化功能更加灵活。

4 算法性能评测与实验分析

4.1 阈值自适应算法评测

为验证本文提出的阈值自适应算法的有效性，采用与软、硬阈值算法进行对比的方式进行评测。选定如下形式的时变含噪信号进行对比分析

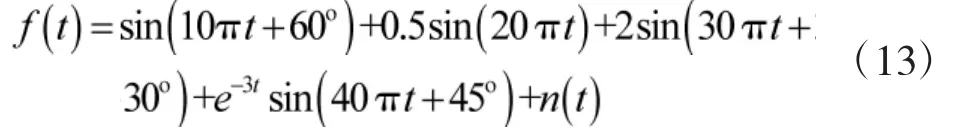
式中，有效信号为多种正弦信号的叠加，n（t）为服从N（0，1）分布的白噪声。

对式（13）所示的信号采用常规连续小波算法进行3层小波分解，对分解系数采用式（8）～式（12）进行阈值的确定与量化，为更好地进行性能测评，利用噪声抑制率和信号失真率［16］两个参数作为评估标准。对比结果如表1，通常情况下，信号失真率越小则表明噪声抑制率越大，即可认为对信号的降噪处理性能就越好。由表1可看出，本文提出的自适应分层阈值确定算法具有较高的噪声抑制率，表明其降噪效果较好。

表1 多种阈值确定算法评价指标比较结果

4.2 测试实验分析

为验证本文算法在机动车辆变速换挡中的实际降噪性能，以配备6挡自动变速器的机动车辆为实验对象，在平直的路面进行连续加、减速行驶，对图1所示的实车节气门位置信号（Throttle Position Signal，TPS）进行降噪处理实验。

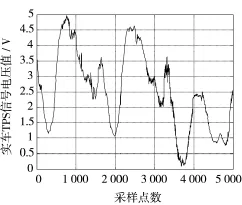
图1 换挡信号TPS采样曲线

选取TPS采样频率fsamp=1 200 Hz，为提高分辨率，取其中的5 000个采样点进行降噪分析，可得q=5、p=4。由m=11可该变换中最小频带宽度Wb_min=2.343 Hz，则由式（7）可确定分解层数为3≤ln≤5。考虑分解计算的复杂度，此处对采样信号进行4层小波分解，其高频部分小波系数d4，1、d4，2、d4，3、d4，4波形如图2所示。

图24 层分解高频系数曲线

选用本文提出的自适应分层阈值降噪改进算法对TPS分层后的信号进行处理，对TPS分解后的信号按式（4）所示进行重构，得到去噪后的信号曲线如图3所示。可看出，波形与原始的信号信息相吻合，波形平稳且有清晰的波峰和波谷，失真度较低。用处理后的换挡信号控制试验车的6速自动变速器，并检测大、中、小节气门下各挡位换挡时刻的冲击度，将检测结果与未进行处理的信号控制相比，各挡位换挡冲击度明显降低。

图3 TPS降噪重构信号曲线

5 结论

本文研究了机动车辆在行驶过程中换挡信号的降噪与重构问题。首先简述了离散小波阈值降噪的原理，之后基于最小带宽离散小波算法，提出了简化的、适用于工程实现的小波分解层数确定方法；然后利用初始阈值对各层小波系数进行分类，利用各层中各类系数均值差的模及均方差为依据，设计了各层阈值的自适应迭代确定算法，同时改进了阈值的量化函数，并将该改进算法应用于机车的挡位信号检测与降噪。仿真对比试验和应用测试结果表明，该算法具有较好的降噪效果，且可很大程度地缩短运算时间。该算法在滤除噪声的同时能较好体现信号细节信息，适合于对实时性和准确性要求较高的机车相关信号检测当中。

［1］宋军，刘渝，王旭东.一种改进的窄带信号降噪算法及其应用［J］.振动与冲击，2013，32（16）:59-62.

［2］王欣，赵达尊.图像噪声对相位变更波前传感的影响研究［J］.光学学报，2009，29（8）:2142-2148.

［3］褚东升，高守婉.带乘性噪声广义系统状态最优估计算法［J］.中国海洋大学学报，2008，38（5）:814-818.

［4］CARY S，CAJETAN M A，PHIL H，et al.An approach to vibration analysis using wavelets in an application of aircraft health monitoring［J］.Mechanical Systems and Signal Processing，2007（21）:1255-l 272.

［5］PICHUGIN K A，SOKOLOVA A G.Application of wave transformation for vibrational diagnostics of scoring in the cylinder-and-piston group of an internal combustion engine［J］.Journal of Machinery Manufacture and Reliability，2007，36（5）:487-492.

［6］张吉先，钟秋海，戴亚平.小波门限消噪法应用中分解层数及阈值的确定［J］.中国电机工程学报，2004，24（2）:118-122.

［7］蔡铁，朱杰.小波阈值降噪算法中最优分解层数的自适应选择［J］.控制与决策，2004，24（2）:118-122.

［8］王维，张英堂，任国全.小波阈值降噪算法中最优分解层数的自适应确定及仿真［J］.仪器仪表学报，2009，30（3）: 526-530.

［9］RAFIEE J，TSE P W，HARIFI A.A novel technique for selecting mother wavelet function using an intelligent fault diagnosis system［J］.Expert Systems with Applications，2009，36（3）:4862-4875.

［10］孙蕾，谷德峰，罗建书.基于迭代方法的软阈值估计小波去噪［J］.系统工程与电子技术，2009，31（1）:36-39.

［11］蒋克荣，唐向清，朱德泉.基于改进阈值小波算法的汽车轮速信号处理［J］.仪器仪表学报，2010，31（4）: 736-741.

［12］谭晓衡，鄢海燕，苏萌.基于自适应小波消噪的数字调制识别优化算法［J］.电子与信息学报，2011，33（2）: 466-469.

［13］BAKHTAZAD A，PLALAZOGLU A，ROMAGNOLI A J. Process data de-noising using wavelet transform［J］.Intelligent Data Analysis，1999（3）:267-286.

［14］IMATIAZ H，FATTAH S A.A wavelet-based dominant feature extraction algorithm for palm-print recognition［J］. Digital Signal Processing，2013，23（1）:244-258.

［15］PHAM V L，WONG K P.Anti-distortio n method for wavelet transform filter banks and non-stationary power system waveform harmonic analysis［J］.IEE Proc.Gener.Transm. Distrib.，2001，148（2）:117-122.

［16］王长龙，朱红运，徐超，等.自适应小波阈值在磁记忆信号降噪处理中的应用［J］.系统工程与电子技术，2012，34（8）:1555-1560.

Improved Discrete Wavelet Transform Algorithm with Applications to Shift Signal De-nosing of Motor Vehicles

GAO Xian-ping，CHENG Ying，WANG Xiang-xin
（Tianjin University of Technology and Education，Tianjin 300222，China）

Aiming at the strong electromagnetic and environment vibration noise which exist in the shift signals of motor vehicles，and considering the requirements of real-time and hardware implementation，this paper proposes the simplified method of determining the layer number of wavelet decomposition based on the minimum bandwidth discrete wavelet algorithm.Then，the initial threshold is used to classify the wavelet coefficients in each layer classification.Moreover，the each layer threshold adaptive iteration algorithm is designed in consideration of mean differences and square errors of coefficients in each layer，and the threshold quantization function is improved.Finally，simulation and application contrast testing results indicates that the algorithm has good noise reduction effect，and is suitable for related signal detection and noise reduction of motor vehicles.

shift signal，minimum bandwidth discrete wavelet，wavelet de-noising，adaptive threshold

TP274

A

1002-0640（2017）04-0149-05

2016-02-05

2016-03-14

国家自然科学基金（51408417）；天津职业技术师范大学科研项目（KJ15-10）；国家级大学生创新创业训练计划基金资助项目（201510066036）

高鲜萍（1982-），女，陕西榆林人，硕士，讲师。研究方向：汽车智能与安全控制技术。