基于战例数据的制胜要素选择方法

赵頔，王跃利，战晓苏

（1.军事科学院军事运筹分析研究所，北京100091；2.武警北京指挥学院，北京100012）

基于战例数据的制胜要素选择方法

赵頔1，2，王跃利1，战晓苏1

（1.军事科学院军事运筹分析研究所，北京100091；2.武警北京指挥学院，北京100012）

针对战争制胜机理定量研究需求，提出了一种基于混合评估的制胜要素选择算法。针对战例数据特点，该算法选择两种过滤方法分别从不同方面对要素全集进行评估排序而后加权得到综合排序结果；将结果作为遗传算法的初始种群，而后以分类精度作为个体适应度函数。选择几种典型的分类器综合比较，筛选出规模较小、性能较好的要素子集。测试结果表明，该算法不仅能有效地减少要素子集规模，还可以进一步提高制胜机理分析模型的准确率和效率。

制胜机理，要素选择，战例数据，过滤法，遗传算法，分类器

0 引言

制胜机理，就是战争诸要素发挥制胜作用的必然过程和方式，也可理解为打赢战争的内在规律和必然途径［1］。战争的胜负是由导致这一事物发生发展的诸多要素共同作用所决定的。比如战争主体、手段、时空条件、行动方法等，都是构成这一复杂事物的重要因素［2］。这些因素中，有的是主要的，有的是次要的，有的直接发挥作用，有的间接发挥作用，因此，研究制胜机理，首先要找出影响战争胜负的关键因素，即制胜要素，以此为基础研究各要素间的相互作用关系、动态发展规律，探寻制胜机理［3］。本文以战例数据库中的战例数据为基础，通过现代数据分析方法，进行制胜要素选择，研究结论可作为后续制胜机理研究的依据。

1 要素选择

1.1 要素选择方法

根据不同的评价准则，要素选择方法主要有两种类型:过滤方法（Filter）和封装方法（Wrapper）。

过滤方法基于评估准则选择要素子集。算法计算效率较高。过滤方法独立于后续使用的建模算法，优点是计算效率高，泛化性能也较好，适于大规模数据集；主要缺点是排名靠前的要素对于具体的建模可能并不是最优的选择；或者需要人为设定阈值，评估结果不客观，无法确保选择出一个规模较小的优化要素子集［4］。

包装方法将分类方法嵌入到要素选择中，直接用选择的要素来训练分类器，通过测试要素子集的分类性能集分类识别率来评价要素子集。它并不要求最优要素子集中的每个要素都是最优的。包装方法比过滤方法识别的准确率更高，效果更好，更能真实反应要素选择的效果，分类器的泛化性能也更优。包装方法的不足是评估子集时需要多次调用学习算法，学习慢，时间开销大。常用的分类器包括神经网络、支持向量机、K最近邻、决策树和朴素贝叶斯等，几种不同类型的分类器还可以集成使用，以提高分类器的泛化能力［5］。

1.2 子集搜索策略

要素选择的大多数方法都要牵涉到在要素空间搜索中最有可能作出类预测的要素子集。搜索方法主要有:全局搜索、顺序搜索和随机搜索。

全局搜索可以保证获得对于给定的评价准则是最优的要素子集，但开销过大。顺序搜索算法虽然能够取得不错的识别效果，但却容易陷入局部极小。随机搜索对问题依赖性小，搜索能力强，可以避免局部最优，并能保证所选要素子集的最优性［6］。总之，这3种方法中只有全局搜索能保证最优，但时间复杂度高，不适合高维情况，后两者以牺牲性能来换取简捷、高效，但不能保证性能最优［7］。

2 基于混合评估的要素选择算法

基于前面提到的要素搜索方法和要素评估标准的基础上，为了得到尽可能最优的要素子集，本文提出基于混合评估的要素选择算法（FSFW，Factor Selection based on Filter and Wrapper）。FSFW算法首先基于两种过滤方法对全部要素进行排序，然后根据综合排序结果作为初始化GA种群的依据，对于每一次产生的新个体训练多个分类器，以分类精度作为个体适应度函数。在上述操作的基础上，选择几种典型的分类器分别进行要素选择得出最优子集。最后，根据综合比较，筛选出数量较少、性能较好的要素子集。

2.1 两种过滤评估方法

本算法采用两种过滤方法进行要素选择，分别是:类可分法、Pearson相关系数。这两种方法根据不同的评价标准评估要素，并产生不同的要素排序。类可分法根据类间距离计算要素的分离度值，该方法计算简单但忽视了要素之间的相关性。Pearson相关系数法使用相关性作为评价标准，根据要素与类之间或要素与要素之间的相关性对要素进行评估。两种方法各取所长，优缺点互补［8-9］。

2.2 算法流程

本算法由两部分构成；第一步采用两种不同的过滤方法从不同的侧面对全部要素进行排序；第二步采用包装方法，此处使用的是随机搜索方法GA（遗传算法）根据排序作为其初始种群的选择依据。GA搜索首先根据排序给每个要素分配一个选择概率，排序越靠前的要素被分配的概率越大，相应的被选中的机会越大。因此，组成初始种群的大部分要素都是在第一步经过过滤后排序靠前的要素。初始种群中个体的适应度函数由多个分类器的分类精度确定，在经过选择、交叉、变异操作后生成新的个体，个体的每一位对应一个要素，经过多次变异后输出适应度最高的个体。该算法的流程如图1所示。

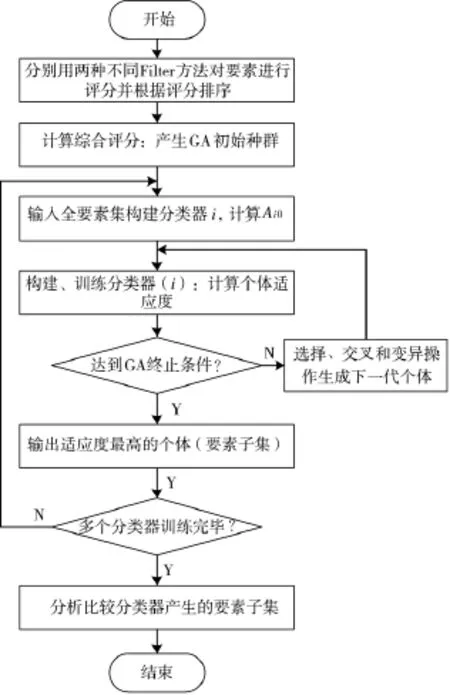
图1 FSFW算法流程

2.3 算法实现

首先采用过滤方法进行评分并进行排序，然后对要素进行综合排序。根据要素的综合排序生成遗传算法的初始种群，最后经过GA操作生成下一代个体，并选用人工神经网络等分类器，构建、训练分类器，根据分类精度输出适应度最高的个体。具体实现如下:

3 实验及结果分析

3.1 战例数据集及预处理

3.1.1 战例数据集

本文采用的战例数据集是美国的概念分析机构CAA和历史评估与研究小组HERO建立的战例数据库CDB90G，该战例库中包含660个战例，每个战例包含146个属性。每个战例的数据是根据历史上空地联合作战的实际数据生成的，尽管该数据集中数据存在空项以及部分数据不是很精确等问题，不过，CDB90G是目前公认的最为有效和权威的数据库，具体的数据集要素定义如表1所示。

表1 战例数据集描述

3.1.2 数据预处理

受目前军事历史研究现状和战例数据的获取途径等方面的制约，构建模型时完全脱离相关领域专家的经验是很难获得具备良好性能模型的。因此，在建模前对战例数据的预处理主要包括以下两个层面:

①军事层面

每个战例都由146个要素进行描述，通过表1可以看出，每项要素是基本要素，比如对于兵力数量就涉及到总兵力、初始兵力、战争过程中增援与替补兵力、伤亡兵力、最终剩余兵力等多项，若增援或替补兵力等于零（数据表中CODE=1时），则剩余兵力=初始兵力-伤亡兵力、总兵力=初始兵力；若增援或替补兵力不等于零（CODE=2或3），则总兵力=初始兵力+增援兵力。类似的情况还有攻守双方采取的战术类型，表中涉及到的战术要素有6项，分别是主战术计划1-3，辅助战术计划1-3，辅助战术计划的制定受主战术计划影响，主辅战术计划1、2、3也互有影响。因此，虽然使用先进的数据分析技术对战例数据进行定量分析过程中也可能分析出要素之间的冗余及关联关系，但是由于战争系统的复杂性与特殊性，在数据预处理阶段抛开要素的具体军事意义仅就数据本身进行处理，显然是欠妥当的。

②数据分析层面

在进行完军事层面的预处理后，再观察数据本身。由于战例数据采集困难，数据集中的数据存在空项以及某些数值型要素数值变化范围大等问题，因此，在进行建模前进行数据层面的数据预处理也必不可少。对数据的预处理方法多种多样，并且也相对成熟，比如对于缺失数据可以采用删除法或插补法等进行处理，对于数值型数据则采用规范化方法进行规范而后再视情况进行离散化处理，对于名词性要素则根据不同要素特点进行赋值。按照上述方法进行完预处理后战例数据集的数据均变为适合分析的规范化的数值要素。

3.2 FSFW算法与其他要素选择算法的比较

为了验证FSFW算法对于战例数据集的适用性，对比测试了该算法与其他要素选择算法的性能。测试分别使用FSFW算法、决策树算法、粗糙集算法和Ludermir算法筛选制胜要素，用神经网络作为分类器评估相应的要素子集。

神经网络参数设置为:学习率0.3，迭代次数100次，均方误差为0.000 1，隐层节点数目15个。表2是FSFW算法与其他要素选择算法的比较结果。对比可知，FSFW算法在要素子集规模选择上不大于其他算法，并且该要素子集在一定程度上提高了分类精度，即两方面均获得不错的效果。

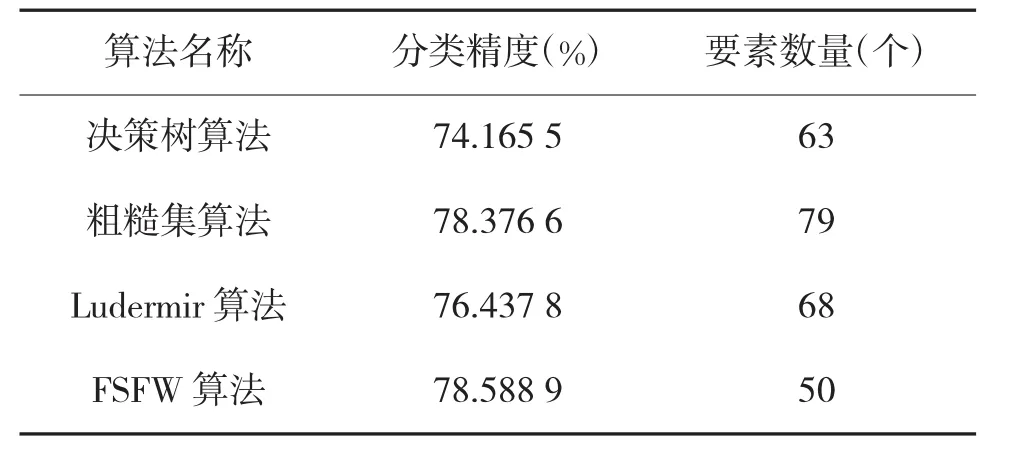
表2 FSFW算法与其他要素选择算法的比较

FSFW算法之所以优于其他3种要素选择算法，原因是FSFW算法在使用filter方法对要素进行评估时，没有设置阈值，将整个要素空间作为GA算法初始化种群的依据，评估了所有可能的要素子集，在进行个体适应度计算时，综合多个分类器的分类精度作为评价标准，最终筛选出最优要素子集。而其他要素选择算法侧重评估要素本身，没有过多考虑要素间以及要素与类间相关关系，没有基于具体分类评估要素子集。

3.3 FSFW算法对分类器分类性能的影响

为了评估FSFW算法对分类器分类性能的影响，在GA搜索阶段分别使用C4.5、BPNN、BaysNet、Logistic、SVM分类器的分类精度作为个体适应度。这5个分类器是军事领域的主流分类器，每个都有鲜明的代表性，能较充分地反映主流算法的性能。

表3 不同分类器的实验结果

GA算法参数设置:种群规模30，迭代次数30，交叉率0.6，变异率0.1。通过实验，得到对应分类器的最高分类精度以及对应的要素个数，结果如表3所示。可以看出，子集规模最小的是采用神经网络作为分类器，分类精度最高的是采用贝叶斯网络作为分类器，但是神经网络分类器的分类精度仅比贝叶斯低0.36%，而子集规模却相差10个，因此，最终实验结果为使用神经网络分类器的分类性能。另外，从表3还可以看出，作为GA算法个体适应度函数，虽然使用不同分类器的分类精度作为评估标准，FSFW算法对于战例数据集都能减少要素数量40%～60%，并且要素数量减少后对于各分类器的分类性能大多有所提高，最差的结果也提高了3.7%的分类精度。这表明，对于战例数据集来说该算法是一种有效的要素选择算法，能够减少要素数量的同时而不降低分类器的分类性能。

3.4 实验结果

GA算法参数设置:种群规模30，迭代次数30，交叉率0.6，变异率0.1。运用FSFW算法筛选制胜要素如表4所示。可以看出，相对于原始数据集的146个要素，FSFW算法筛选出的要素子集规模为50个，要素数量减少了65.75%，分类精度为78.59%，对应的分类器为神经网络分类器，对于战争这样一个复杂巨系统，能够达到75%以上的分类精度，已经是比较理想的结果。这些制胜要素能够帮助军事专家在定量分析制胜机理，构建制胜模型时有效去除战例数据集中与战争制胜相关性不大或冗余的要素，同时也降低了后续收集数据的难度，尤其是当样本量有限的情况下，这样有助于专家集中注意战例的关键要素，以获得效率更高的分析过程。不过，随着战例数据的不断采集，战争形态的不断变化，影响战争制胜的要素也在不断变化，因此，本实验结果仅对本文所使用的战例数据集有效。

表4 制胜要素

4 结论

本文结合战例数据的特点，在过滤法评价单一要素的基础上，搜索对应的整个要素空间。由于过滤方法对分类的性能考虑较少，因此，选择分类性能作为划分选择要素子空间的客观依据。并且因为战例数据的多模式，目前为止还没有一种能够满足战例数据特性的且功能显著的分类器。为此我们将目前在军事研究尤其是在战例数据研究中常见的分类器挑选出来，综合对比考虑，最后选择几种进行集成，以期获得性能最佳的分类器，同时，还将要素间的相关性和冗余性纳入考量范围，以减少要素间存在的重复，提高后续研究的效率。

［1］任海泉.深入研究现代作战制胜机理不断创新作战指导［J］.军事学术，2014（1）:6-10.

［2］张世平，陈荣弟.信息化战争制胜机理问题研究［J］.军事学术，2014（5）:5-16.

［3］王永华.关于作战数据几个问题的认识［J］.中国军事科学，2014（1）:96-103.

［4］PENG Y，WU A，JIANG J.A novel feature selection approach for biomedical data classification［J］.Journal of Biomedical Informatics，2010，43（1）:15-23.

［5］ENZHE Y U，SUNGZOON C H O.Ensemble based on GA wrapper feature selection［J］.Computer&Industrial Engineering，2006，51（1）:111-116.

［6］KUDO M，JACK S.Comparison of algorithms that select feature for pattern classifiers［J］.Pattern Recognition，2000，3（1）:25-41.

［7］QIAN W B，SHU W H.An incremental algorithm to feature selection in decision systems with the variation of feature set［J］.Chinese Journal of Electronics，2015（1）:225-231.

［8］张岐龙.基于特征空间中类别可分性判据的特征选择［J］.火力与指挥控制，2010，35（6）:79-84.

［9］高鹏毅.一种使用多Filter初始化GA种群的混合特征选择模型［J］.小型微型计算机系统，2012，33（11）: 2379-2384.

Research on Method of Winning Factors Selection Based on Data of Battle Cases

ZHAO Di1，2，WANG Yue-li1，ZHAN Xiao-su1
（1.Academy of Military Science，Operations Research Institute，Beijing 100091，China；2.Beijing Command College of Armed Police Force，Beijing 100012，China）

For the Demand of factor selection in quantitative study of winning mechanism，and considering the inadequaces of traditional methods，a new factor selection model based on filterwrapper is proposed to select the decisive factors in war.The model combines two filters to pre-rank all the variables in the battle cases dataset from different aspects，and then produce an initial GA population based on it.In the wrapper，Genetic Algorithm is selected to search the factor subsets.In GA，individual fitness degree is evaluated by classification accuracy of multi-classifier，which can help find the subsets with both of smaller size and better performance.Tests demonstrate that the FSFW model not only can reduce dimensionality of factor subset，but also can improve the accuracy and efficiency of winning models.

winning mechanism，factor selection，data of battle cases，filter，GA，classifier

E911

A

1002-0640（2017）04-0018-05

2016-03-05

2016-04-23

全军军事类研究生基金资助项目（2014JY637）

赵頔（1982-），女，辽宁沈阳人，博士生，讲师。研究方向：数据工程。