双经纬仪异面交会目标点的空间位置估计*

霍李，王媛

（中国白城兵器试验中心，吉林白城137001）

双经纬仪异面交会目标点的空间位置估计*

霍李，王媛

（中国白城兵器试验中心，吉林白城137001）

针对双经纬仪异面交会中目标点并不一定正好在公垂线上的问题，提出了在公垂线附近的空间区域上估计目标点位置的方法。该空间区域为以公垂线为对角线，各边分别平行于双经纬仪测量坐标系三轴的长方体空间区域。在目标点位置估计时考虑到经纬仪高低角与水平角测角精度的不同，以及目标点与经纬仪之间距离对空间点坐标精度的影响。采用蒙特卡洛方法模拟结果表明:新方法的目标点空间位置估计精度不亚于传统公垂线法，在特定情况下甚至能提高5%以上。模拟结果验证了新方法的可行性和有效性。

工程测量技术，双经纬仪，异面交会，权系数，位置估计，蒙特卡洛方法

0 引言

电子经纬仪作为一种高精度、易操作的通用仪器在现场检测中已广泛使用，其中双经纬仪交会测量法已在靶场火炮试验的多个检测项目上得到应用，如调炮精度［1-3］、炮身偏移量［4］和复瞄精度［5］等。通常都是通过优化双经纬仪布站［5-7］来保证该方法的检测精度。文献［8］在优化布站的基础上，通过增加身管上标记点的数量构成大量冗余测量数据，采用最小二乘算法进行空间直线拟合得到身管指向，测量精度有明显提高。文献［9］将动态目标跟踪测量领域中的“异面交会”思想引入火炮检测领域，通过数据处理就实现了身管指向测量精度的改善。但是，目前在经纬仪异面交会的数据处理时往往局限在公垂线上估计目标点的位置［9-12］，而实际上，目标点的位置并不一定正好在公垂线上。

本文在公垂线附近的空间区域上估计目标点的位置，并且在目标点位置估计时充分考虑到经纬仪高低角与水平角测角精度的不同，以及目标点与经纬仪之间距离对空间点坐标测量精度的影响。

1 双经纬仪交会测量

1.1 共面交会测量

双经纬仪共面交会测量原理［1］如图1所示，2台电子经纬仪中心T1和T2间的距离为b，则有T1（0，0，0）和T2（b，0，0）。瞄准同一目标点P，观测得到一组水平角和俯仰角（α1，β1，α2，β2），则点P（x，y，z）的空间坐标与观测角有式（1）的关系。

图1 共面交会测量

1.2 异面交会公垂线估计法

在实际检测中，2台经纬仪的视轴往往并不相交，为异面关系。目前的方法［9-12］是在2条异面直线的公垂线上估计目标点P的坐标，为便于叙述称之为“公垂线估计法”，如图2所示。

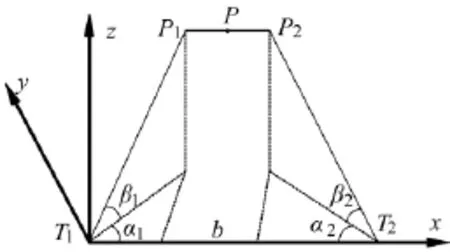
图2 异面交会公垂线估计法

在图2中，设经纬仪视轴所在的2条异面直线的公垂点分别为点P1和点P2，由于点T1和点T2的坐标已知，因此，可列出2条视轴T1P1和T2P2的点向式方程，分别见式（2）和式（3）。

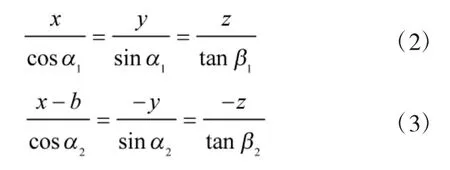
根据异面直线和公垂线的垂直关系，由式（2）和式（3）可得异面直线2个公垂点的坐标为。其中，l1、l2为方程参数，其表达式为:

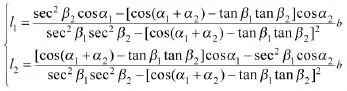
在估计目标点P的坐标时，设置点P1的权系数为ρ，则点P2的权系数为1-ρ。按式（4）估计出目标点P（x，y，z）在公垂线上的位置。

在权系数ρ的选取上，通常采用的是“公垂线中点法”（本文简称“中点法”，即取ρ=0.5），该方法简单、适用范围广，但是没有考虑到各经纬仪测角精度以及各经纬仪至目标点距离的不同，在对精度要求高的场合不适用。

文献［10-11］考虑到各经纬仪测角精度的不同，权系数ρ按式（5）计算。

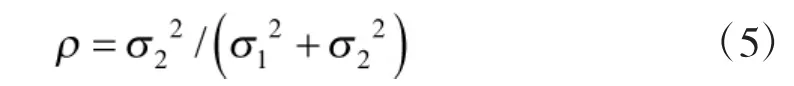
式中，σ1、σ2分别为经纬仪的测角精度。

文献［9，12］综合考虑到经纬仪的测角精度和经纬仪到目标点的距离这2个因素对目标空间点坐标精度的影响，权系数ρ分别按式（6）［9］和式（7）［12］计算。

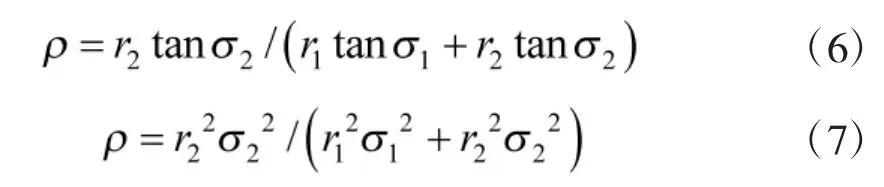
式（6）和式（7）中，r1、r2分别为经纬仪T1、T2到公垂点P1、P2的距离。

上述方法都是限定在公垂线上估计目标点的坐标。并且都没有考虑到，即使是同一台经纬仪，其水平角和俯仰角的测角精度也可能不相同的情况。

2 空间区域内的目标点位置估计

实际上，目标点的位置并不一定正好在公垂线上，更有可能处于公垂线附近的空间区域内。由于2个公垂点的坐标可以解算，因此，本文设定的目标估计点所在的空间区域为:以公垂线为对角线的长方体，各边分别平行于测量坐标系的3条轴线，如图3所示。

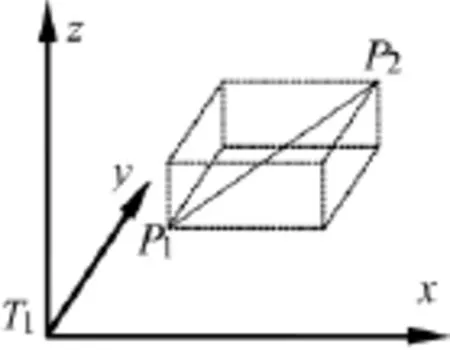
图3 目标点的估计空间区域

以经纬仪T1观测目标点P为例，设经纬仪理想视轴T1P在水平面T1-xy上的投影为线T1P'，其中目标点P在水平面T1-xy上的投影为点P'；经纬仪实际视轴在水平面T1-xy上的投影为线T1P1'。以点P'为垂点的垂线与T1P1'相交于点P1'，则线段P'P1'在x轴和y轴上的投影为σx1和σy1，如图4（a）所示。在经纬仪理想视轴T1P所在的垂面上，直线T1P绕点T1旋转σβ1得到直线T1P1''，点P1''为以点P为垂点的垂线与T1P1''的交点，则线段PP1''在z轴上的投影为σz1，如图4（b）所示。

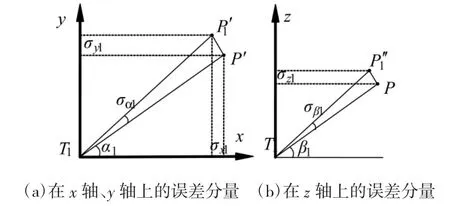
图4 空间误差在3轴上的分量示意图

空间误差在测量坐标系3个轴上的分量按式（8）计算。

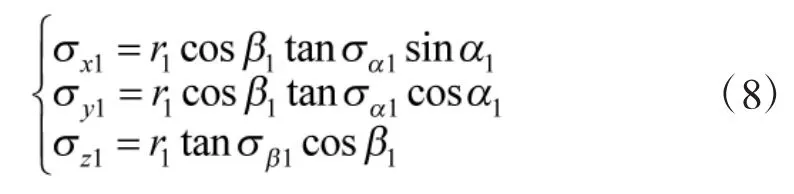
式中，σα1、σβ1分别为经纬仪T1水平角和俯仰角的测角精度。

同理计算出经纬仪T2瞄准目标点P的空间误差分量σx2、σy2、σz2。

经纬仪T1瞄准目标点P在测量坐标系3个轴上的权重ρx、ρy、ρz按式（9）计算。

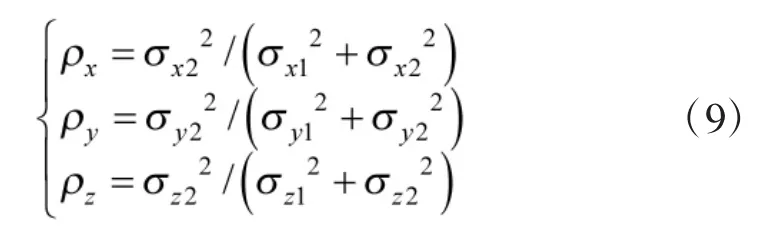
按式（10）估计出目标点P（x，y，z）在公垂线附近空间区域内的位置。

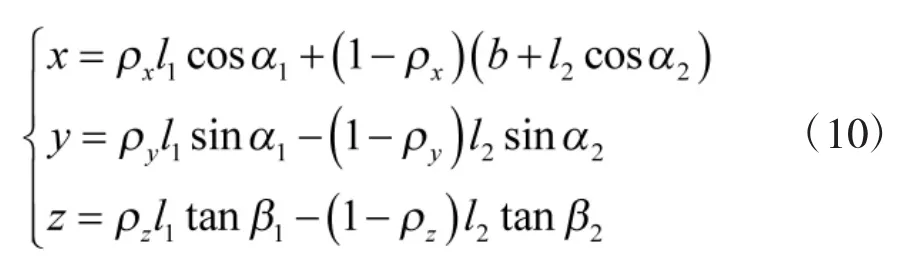
3 模拟分析

3.1 基于Monte Carlo方法的测量精度评定步骤

步骤1构建1个空间点的坐标（x0，y0，z0），通过式（1）计算出对应的经纬仪观测角理论值（α1'，α2'，β1'，β2'）。

步骤2选取合适的经纬仪测角精度σ仿真出测量过程中经纬仪观测角的1组伪随机数（εα1，εα2，εβ1，εβ2）。

步骤3将经纬仪观测角理论值加上仿真出的经纬仪观测角的伪随机数，得到经纬仪测量过程的“伪观测角”（α1，α2，β1，β2）T=（α1'，α2'，β1'，β2'）T+（εα1，εα2，εβ1，εβ2）T。

步骤4将经纬仪的“伪观测角”分别代入式（4）或式（10），按不同方法选取权系数ρ解算出测量点坐标各1组模拟样本。

步骤5重复步骤2～步骤4的过程m次，计算得到不同方法解算的测量点坐标各m组模拟样本。对样本进行统计，分别得到三维空间坐标的测量均方差δx、δy和δz，如式（11）、式（12）和式（13）所示。并按式（14）计算测量点坐标的测量均方差δP。

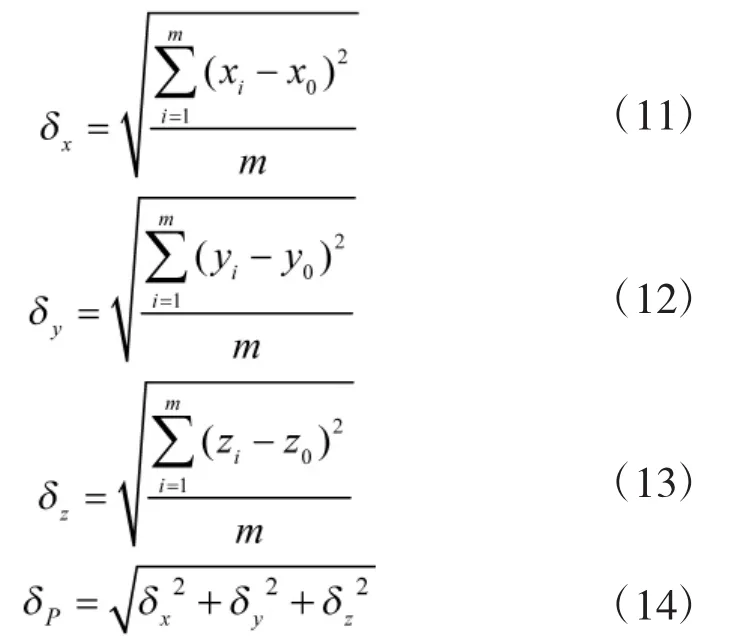
步骤6比较不同的权系数ρ解算的测量点坐标的测量精度。

3.2 Monte Carlo模拟分析

取2台经纬仪间的距离b=10 000 mm。在经纬仪测量坐标系中的选取2个点，其中，点A（5 000，6 000，300）距2台经纬仪的距离相同，点B（15 000，6 000，300）到2台经纬仪的距离差异明显，单位为:mm。

将点A和点B的坐标值分别代入式（1）计算出目标点A和B对应的经纬仪理论观测角，如下页表1所示。

表1 标记点的经纬仪观测角理论值

3.2.1 经纬仪的水平角和俯仰角的测角精度相同

分别取经纬仪测角精度σ为2''和5''，随机抽样106次。分别用在公垂线上估计目标点的“中点法”、文献［9-12］以及本文方法进行解算，结果如表2所示。

表2 不区分经纬仪水平角和俯仰角精度的目标位置估计均方差

表2的结果表明:在经纬仪测角精度相同时，对不受距离因素影响的点A的估计结果各方法结果基本相同；对受距离因素影响的点B的计算结果明显不同，其中本文方法与公垂线法中表现最佳并且结果相当；在经纬仪测角精度不同时，除了“中点法”的估计精度相对较差外，其他3种方法的结果相近。

因此，在不区分经纬仪水平角和俯仰角精度时，本文目标点位置估计精度始终不低于在公垂线上估计目标点的方法。

3.2.2 经纬仪的水平角和俯仰角的测角精度不同

由于文献［9-12］的方法没有考虑到经纬仪的水平角和俯仰角的测角精度可能不同的情况，因此，只对“中点法”和本文方法进行比较，随机抽样106次，结果如表3所示。

表3 区分经纬仪水平角和俯仰角精度的测量均方差

表3的结果表明，当高低角与水平角测角误差不同时，本文方法的空间点位置精度始终不低于公垂线中点法，在特定情况下甚至能提高5%以上。

4 结论

本文在公垂线附近的空间区域上估计目标点位置，不仅考虑了经纬仪测角精度和目标点到经纬仪的距离变化对空间点坐标精度的影响，而且区分了经纬仪水平角和俯仰角测角精度不同的情况。模拟结果表明，本文方法的点位置估计精度最优。为进一步提高双经纬仪空间点坐标的检测精度提供了新思路。

［1］陶化成，张卫民，黄小平，等.压制兵器身管指向测试系统［J］.测控技术，2001，20（8）:20-22.

［2］罗鸿飞，张英堂，任国全，等.基于空间坐标解算的火炮调炮精度检测方法研究［J］.火炮发射与控制学报，2007，28（3）:50-52.

［3］李平，王英.基于数字式经纬仪检测的调炮精度测量装置［J］.火力与指挥控制，2010，35（Z1）:96-98.

［4］傅建平，李国章，石志恿.火炮瞄准线偏移量检查新方法及其精度分析［J］.火炮发射与控制学报，2002，23（2）: 39-42.

［5］董起顺，姜涛，苏成志.火炮复瞄精度测试中经纬仪的最佳布站研究［J］.兵工学报，2007，28（5）:513-515.

［6］张光，任国全，张英堂，等.调炮精度检测中双经纬仪优化布站方法［J］.火力与指挥控制,2011，36（9）:176-179.

［7］孙泽林，王昭，翟唤春，等.双经纬仪交会测量火炮调炮精度的误差分析与抑制［J］.光学精密工程，2011，19（10）: 2434-2441.

［8］王媛，霍李，宫新宇，等.基于多点空间直线拟合的调炮精度检测方法［J］.火力与指挥控制，2015，40（3）:130-133.

［9］王媛，霍李，赫赤，等.考虑异面交会因素的调炮精度数据处理方法［J］.火炮发射与控制学报，2015，36（2）:77-81.

［10］侯宏录，李宏.光电经纬仪测量飞行器三维坐标方法及误差分析［J］.光电工程，2002，29（3）:4-8.

［11］吴能伟，陈涛.异面交会法在光电经纬仪中的应用［J］.仪器仪表学报，2006，27（Z2）:1233-1235.

［12］杨增学.常规兵器试验交会测量方法及应用［M］.西安:西安交通大学出版社，2010:79-80.

Target Point Position Estimation for Double-theodolite Non-uniplanar Intersection

HUO Li，WANG Yuan
（Baicheng Ordnance Test Center of China，Baicheng 137001，China）

Aimed at the problem that the target point not just in the common vertical line for double-theodolite non-uniplanar intersection，a method of estimating the target point position nearby spatial region of the common perpendicular is presented.The spatial region is the cuboid spatial region that taking the common perpendicular as diagonal，and each side separately parallels with doubletheodolite measurement coordinate system triaxiality.When estimated the target point position，in consideration of the difference of angular accuracy that theodolite azimuth angle and pitching angular，and in view of the distance between target point and theodolite influence on space point coordinates precision，the simulation result of adopting the Monte Carlo method shows that the spatial point position precision of the new method is not inferior to the traditional methods that estimate the object points position on the common perpendicular，even improved by above 5%in a specific state.The results show that the new method is feasible and available.

engineering survey technology，double-theodolite，non-uniplanar intersection，weight coefficient，position estimation，Monte Carlo method

TJ06

A

1002-0640（2017）04-0138-04

2016-02-24

2016-03-19

国家军用标准修订项目（14ZS021）；军队试验技术研究基金资助项目（12-sy14）

霍李（1979-），男，重庆人，硕士，工程师。研究方向：火炮静态检测技术。