不同干扰对QSPK解调性能的影响分析*

秦伟，王可人，金虎，钱锋

（电子工程学院，合肥230037）

不同干扰对QSPK解调性能的影响分析*

秦伟，王可人，金虎，钱锋

（电子工程学院，合肥230037）

随着数字卫星通信的快速发展，QPSK作为数字卫星通信系统中一种重要的调制方式，其解调性能也受到越来越多的关注。主要分析QPSK信号在已调干扰信号下的解调性能，并推导出使得QPSK调制信号解调性能最差的干扰信号的统计分布，而且此时统计分布符合QPSK调制方式干扰信号的特征。最后通过实验仿真分析得出信噪比未超过一定值时QPSK调制信号在QPSK调制干扰信号下解调性能最差，并与不同已调制干扰和AWGN干扰下的解调性能作比较。

正交相移键控，干扰，解调，调制

0 引言

19世纪80年代中期以后，正交相移键控技术（Quadrature Phase Shift Keying，QPSK）以其频谱利用率高、高误码率性能和抗干扰性能强，而被广泛应用于数字无线通信、数字移动通信和数字卫星通信中［1-3］。例如，在考虑频带受限以及通信容量需求增加的时候，QPSK是传统卫星通信系统中最佳调制技术［4］。现在复杂的电磁环境中存在不同调制方式的干扰信号（有源干扰或是无源干扰），这对QPSK解调系统会造成影响并使通信系统性能恶化［3］。因此，研究QPSK信号在采用不同调制方式的干扰信号下的解调性能十分重要，可以为抗干扰的策略提供参考，同时也可以为数字卫星通信系统和移动通信系统提供理论依据和设计参考。

目前的研究，考虑针对QPSK干扰的调制方式选择对解调性能的影响分析比较少。文献［4-5］分析了相位噪声对Coherent-QPSK以及DPSK解调系统的影响，并推导出在相位噪声影响下的理论误码率计算公式。文献［6］建立了考虑单音干扰的QPSK模型，从理论角度分析了单音干扰的不同参数对QPSK解调性能产生影响的原理。文献［7］建立相位噪声的系统模型，并指出它不同于热噪声对QPSK系统的影响，是一个非加性过程，而且它是典型的窄带干扰。与上述文献提到的不同，本文主要分析在干扰对齐的前提下，干扰调制方式的选择对QPSK解调性能的影响，并与已有的干扰样式作比较。

本文通过建立分析模型分析在相干条件下和非相干条件下使得QPSK解调性能最差的干扰信号统计分布，并根据统计分布指出它的调制方式。最后通过实验仿真验证结论，并与采用不同调制方式的干扰和AWGN干扰下的解调性能作比较。

1 分析模型

假设传送信息的通信信号调制方式已知，等效低通的发射信号表达式为:

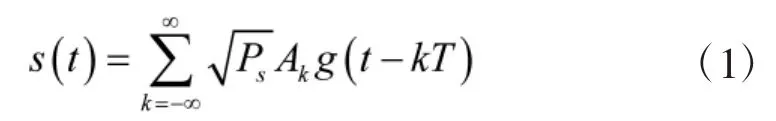
其中，Ps是接收通信信号的平均功率；g（t）表示脉冲形状；T表示码元宽度；Ak表示符合某一调制方式的已调制符号，Ak服从分布且取值为复数，并假设其在星座图中所有星座点均匀取值。为了不失一般性，假设g（t）的能量和已调符号Ak的能量E（|Ak|2）都归一化为1。

干扰信号的等效低通表达式为:

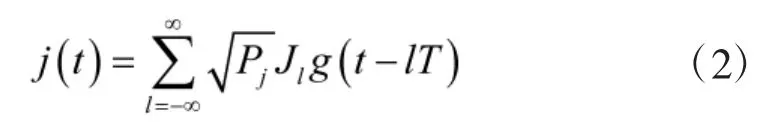
其中，Pj表示接收机处干扰信号的平均功率；g（t）表示脉冲形状；T表示码元宽度；Jl表示符合某一调制方式的已调制符号，分布为假设E（|Jl|）2≤1。

假设信道背景噪声为AWGN噪声，接收机相关接收。那么接收到的信号在通过匹配滤波器以后，然后在一个符号间隔内抽样值为:

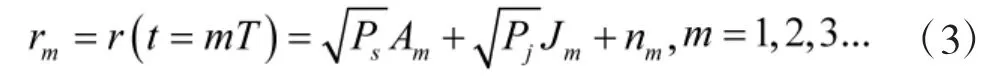
其中，nm是零均值的AWGN噪声，方差为σ2。已调制符号Am、干扰信号Jm和噪声nm三者之间相互统计独立。

用最大似然检测方法，接收机输出端的误码率可以表示如下:

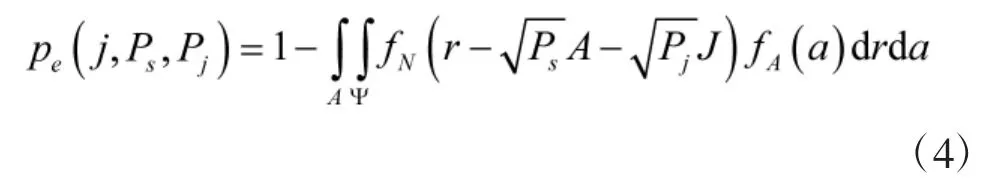
其中，r表示接收信号；j表示干扰信号；Ψ表示信号A的最大似然判决区域。例如，如果信号电平为±L，当A=-L时，Ψ＜0；当A=L时，Ψ＞0。

在给定Ps和Pj的基础上，使得解调性能最差（也就是误码率最大）的优化问题可以表示如下:

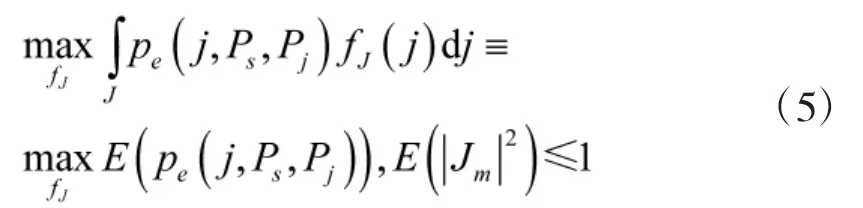
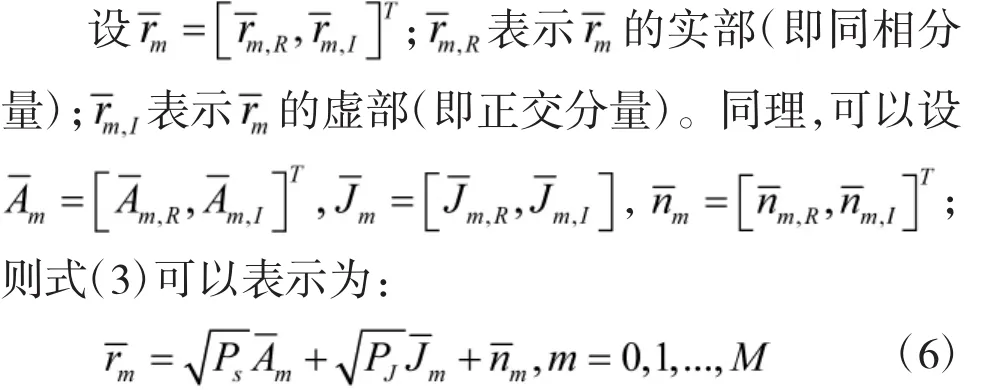
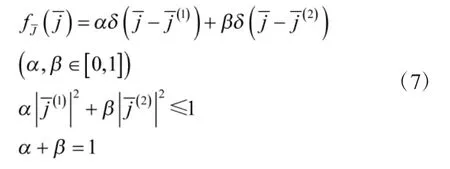
其中，α、β分别表示发送j¯（1）和j¯（2）的概率。因此，寻找使得QPSK解调性能最差的干扰信号统计分布的问题现在变成了寻找α、β、j¯（1）和j¯（2）的问题。

1.1 QPSK信号在相干条件下的解调性能分析

假设干扰信号与通信信号相干且时间同步（理想条件），并且假设接收机没有关于干扰机的先验知识，则接收机仍然按照无干扰时的判决区间进行数据检测。此时QPSK信号可以看作两路相互独立的正交信号（同相分量和正交分量）［10］。则QPSK信号任意一维的差错概率可以表示为关于干扰信号j的函数，如下所示:

证明:

证毕

当干扰信号为AWGN噪声时，j服从高斯分布，则误码率为:

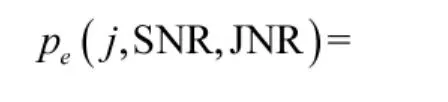
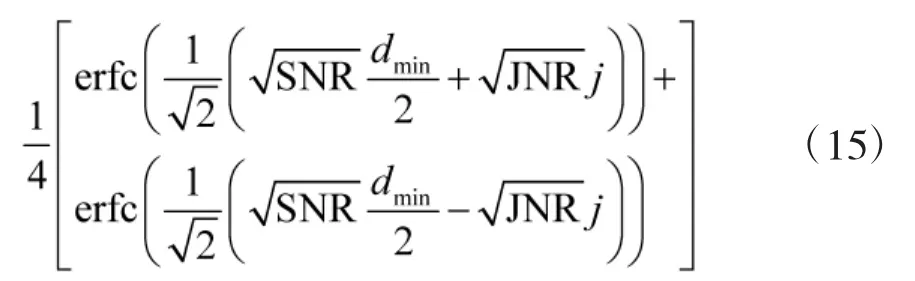
分别把式（14）和式（15）对SNR求导得到它们的比例常数:

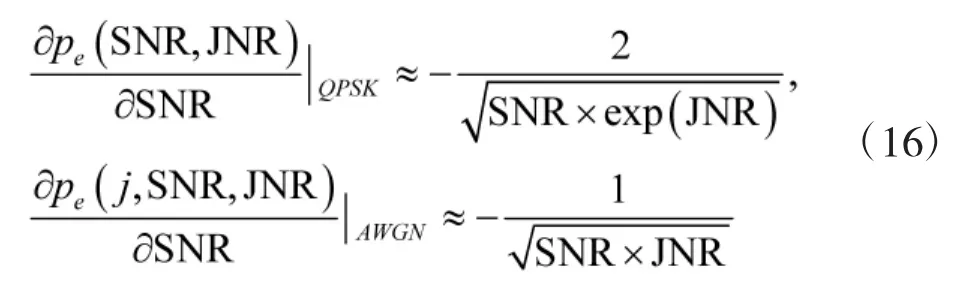
1.2 QPSK信号在非相干条件下的解调性能分析

假设干扰信号与通信信号之间存在随机的相位偏移，那么接收信号式（6）可以表达为:

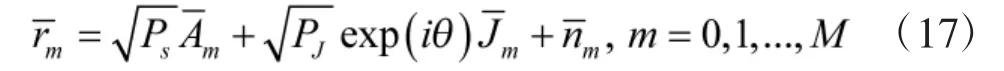
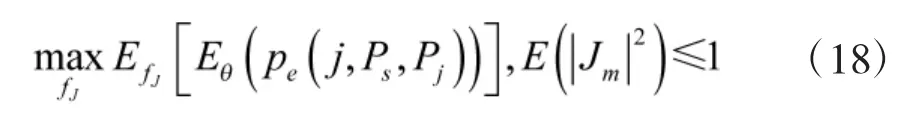
在非相干条件下，QPSK信号仍然可以看作两路相互独立的正交信号（同相分量和正交分量）。此时QPSK信号任意一维的差错概率可以表示为:

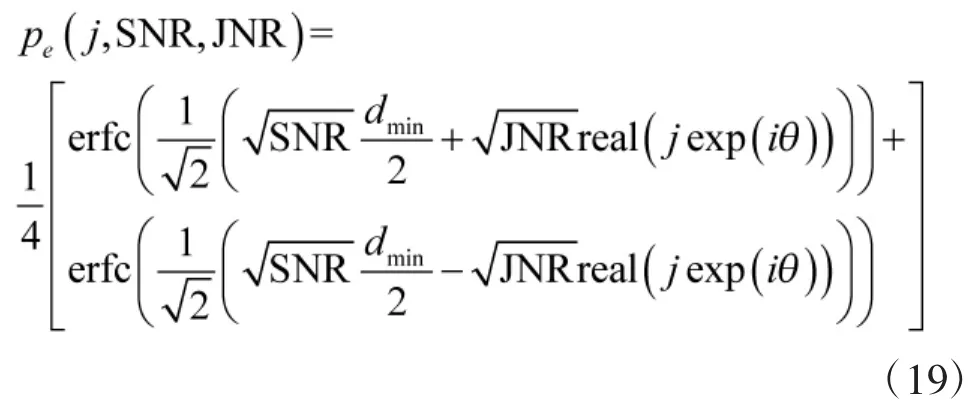
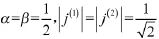
2 仿真实验及分析

仿真实验是基于干扰对齐的基础上进行，与编码方式以及波特率的选择无关。

实验1:仿真分析理想条件下QPSK信号在QPSK、16QAM、2FSK、MSK和AWGN信号干扰下的解调性能，仿真条件为:JNR=10 dB；SNR为5 dB～30 dB；背景噪声为AWGN噪声。仿真结果如图1所示。

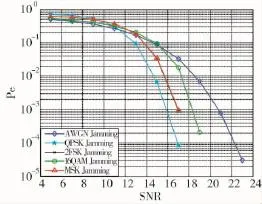
图1 理想条件下QPSK在不同干扰下的解调性能

从图1中可以看出，在SNR未超过11.5 dB时（此时SJR为1.5 dB），QPSK信号在采用QPSK调制的干扰下的解调性能比在AWGN干扰下的解调性能差；在SNR未超过11 dB时（此时SJR为1 dB），QPSK信号在采用QPSK调制方式的干扰下的解调性能比在采用16QAM调制方式的干扰下的解调性能差；在SNR未超过9.6 dB时（此时SJR为-0.4 dB），QPSK信号在采用QPSK调制方式的干扰下的解调性能比在采用2FSK和MSK调制方式的干扰下的解调性能差；从而验证了上述的结论。

实验2:仿真分析非相干条件下QPSK信号在QPSK、16QAM和AWGN信号干扰下的解调性能，仿真条件为:JNR=10 dB；SNR为5 dB～30 dB；相位偏移π/8；背景噪声为AWGN噪声。仿真结果如图2所示。

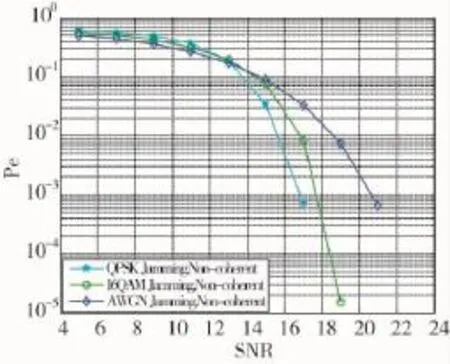
图2 非相干条件下QPSK在不同干扰下的解调性能

从图2中可以看出，在非相干条件下，SNR未超过13.15 dB时（此时SJR为3.15 dB），QPSK信号在采用QPSK调制方式的干扰下的解调性能比在AWGN干扰下的解调性能差；在SNR未超过12.37dB时（此时SJR为2.37 dB），QPSK信号在采用QPSK调制方式的干扰下的解调性能比在采用16QAM调制方式干扰的解调性能更差；从而验证了上述理论分析得到的结论。

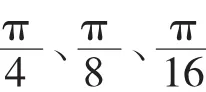
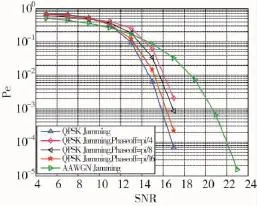
图3 QPSK在不同相偏干扰下的解调性能

从图3中可以看出，即使存在相位偏移，在SNR未超过一定值时，在采用QPSK调制方式的干扰信号下的QPSK解调性能仍然比在AWGN干扰下的解调性能差。从而验证了上述的理论分析。

3 结论

本文在理想条件下和非相干条件下分析了QPSK调制信号在采用不同调制方式干扰下的解调性能并得到结论:在信噪比远小于干噪比时，使得QPSK信号的解调性能最差，干扰信号所采用的调制方式是QPSK。通过实验仿真分析了QPSK信号在采用不同调制方式干扰下的解调性能，并验证了所得到的结论。本文研究对工程实践具有一定的指导意义。

［1］杨小牛，楼才义，徐建良.软件无线电原理应用［M］.北京:电子工业出版社，2001.

［2］TRIKHA M，SHARMA N，SINGHAL M.BER performance comparison between QPSK and 4-QA modulation schemes［J］.MIT International Journal of Electrical and Instrumentation Engineering，2013，3（2）:62-66.

［3］CHOUHAN A K，VATS A.Comparative analysis of inter satellite links using free space optical communication with OOK and QPSK modulation techniques in turbo codes［J］.IJITR，2015，3（4）:2248-2252.

［4］洪磊，杨育红，张瑞.QPSK最佳干扰研究与仿真［J］.通信技术，2009，42（2）:8-11.

［5］POISEL R A.Introduction to communication electronic warfare systems［M］.London:Artech House，Inc.2008.

［6］HAMAGUCHI K，SHOJI Y，OGAWA H.BER performance of coherent-QPSK transmissi-ons affected by phase noise from frequency converters［C］//Vehicular Technology Conference，2001.VTC 2001 Fall.IEEE VTS 54th.IEEE，2001，4:2281-2284.

［7］CORVAJA R，PUPOLIN S.Effects of phase noise spectral shape on the performance of DPSK systems for wireless applications［J］.Europe-an transactions on telecommunications，2002，13（3）:203-210.

［8］杨豪，颜青，刘会来.单音干扰对QPSK解调性能影响分析［J］.无线电工程，2014（4）:54-57.

［9］TAGGART D，KUMAR R.Impact of phase noise on the performance of the QPSK modulated signal［C］//Aerospace Conference，2011 IEEE.IEEE，2011:1-10.

［10］GOKEN C，GEZICI S，ARIKAN O.Optimal stochastic signaling for power-constrained binary communications systems［J］.Wireless Communications，IEEE Transactions on，2010，9（12）:3650-3661.

［11］DULEK B，GEZICI S.Detector randomization and stochastic signaling for minimum probability of error receivers［J］. Communications，IEEETransactionson，2012，60（4）: 923-928.

［12］PROAKIS J G，SALEHI M.Digital communica-tions［M］. NewYork:McGraw-Hill，2008.

［13］COVER T M，THOMAS J A.Elements of infor-mation theory［M］.New Jersey:John Wiley&Sons，2012.

Analysis on Different Jamming Effects on QPSK Demodulation Performance

QIN Wei，WANG Ke-ren，JIN Hu，QIAN Feng
（Electronic Engineering Institute，Hefei 230037，China）

With the rapid development of digital satellite communication，QPSK become an important modulation of digital satellite communication system，and its demodulated performance has been given more and more public concern.The demodulated performance of QPSK signal is mainly analyzed under the digital modulated jamming，and the statistical distribution of jamming signal make demodulated performance worst，and the statistical distribution also accords with the characteristics of QPSK modulated signal.Numerical results are presented in order to validate the theoretical inferences presented and compare it with various modulated jamming and AWGN jamming.

QPSK，jamming，demodulation，modulation

TN91

A

1002-0640（2017）04-0128-05

2016-03-04

2016-04-29

国家自然科学基金资助项目（61171170）

秦伟（1995-）男，安徽宿州人，硕士生。研究方向：数字通信。