基于熵最小化的LFM信号调频率估计算法

袁园，蔡啸，郭蓓蓓

（中国洛阳电子装备试验中心，河南洛阳471003）

基于熵最小化的LFM信号调频率估计算法

袁园，蔡啸，郭蓓蓓

（中国洛阳电子装备试验中心，河南洛阳471003）

利用LFM信号频谱的熵随着调频率减小而降低的性质，提出了一种基于频谱熵最小化的LFM信号调频率的估计SEM方法。建立参数待估的相位补偿因子，通过搜索得到使得补偿后信号频谱熵全局最小的调频率估值。在搜索过程中，采用两级搜索策略，并引入牛顿迭代算法，有效降低了算法复杂度。理论推导和仿真结果证明，该算法为有偏算法，估计偏差量与初始频率相关，理论估计方差比较CR下界低12dB。对雷达实测回波信号进行验证，与离散多项式变换算法相比发现，提出算法估计的鲁棒性更好，并具有较高的测速精度，具有一定的应用价值。

LFM信号，最小熵，有偏估计，Cramer-Rao下界

0 引言

线性调频（Linear Frequency Modulation，LFM）信号以其良好的时域压缩特性和大的发射能量等诸多优点，在雷达、声呐、生物医学及通信工程等领域得到了广泛应用。LFM信号参数估计问题，特别是调频率的估计问题一直是信号处理领域研究的热点问题。

LFM信号的调频率估计方法中，最大似然方法（Maximum Likelihood Estimator，MLE）［1］较早提出，MLE是一种渐进无偏的估计方法，在较高信噪比条件下，其估计性能可以达到Cramer-Rao（CR）下界，但在估计过程中，需要进行二维（频率-调频率维）搜索，运算量较大。目前，学者们提出了很多LFM信号调频率估计方法。文献［2］中提出了离散多项式变换（Discrete Polynomial Phase Transform，DPT）法，DPT算法是MLE的改进算法，并且DPT算法估计LFM信号调频率仅需一次向量复乘、一次FFT和一次频谱最大值的搜索，计算复杂度较MLE大大降低。Gabor展开［3］和短时傅里叶变换（Short Time Fourier Transform，STFT）均基于Fourier变换的时频分析方法，通过分析LFM信号在时频平面的分布特性估计调频率，此类采用时域加窗的方式提高时间分辨率，但会降低频域分辨率。Wigner-Ville变换［4-5］是二阶的时频处理方法，在能量聚集方面，Wigner-Ville变换性能最优，但在多分量信号的条件下，会产生严重的交叉项干扰问题。经验模式分解（Empirical Mode Decomposition，EMD）［6］方法能够在多分量信号中有效地提取不同分量的信号，提高信号信噪比，但由于算法的特殊性，对于采样率、估计性能等方面没有明确的理论分析和指导准则。目前，大多数调频率估计方法都是基于信号的时域特性或者时频特性开展的。

与传统方法不同，本文以LFM信号频谱熵的特性为研究对象，提出了一种基于最小熵准则的调频率估计算法。

1 SEM算法基本原理

本节将着重介绍SEM算法估计信号调频率的基本原理。

线性调频信号为

其中，b0为信号幅度，θ0为初相位，f0为信号频率，为时间宽度，α0为信号调频率，不失一般性，令α0＞0，θ0=0，对信号做傅里叶变换，得

式中

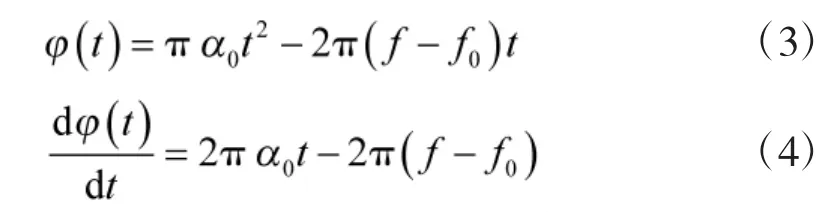
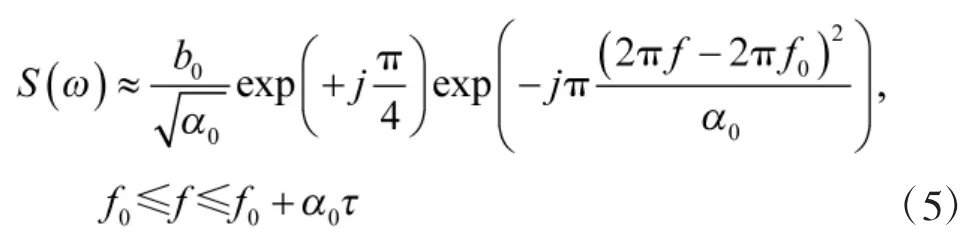
在信号处理中，熵可以用来描述序列分布的平缓程度，序列的熵越大，说明分布越平缓，反之则越尖锐。对于离散LFM信号

式中，Ts为采样时间间隔，N为信号采样点数，其离散傅里叶变换结果为S（k），S（k）的熵的定义为［7］

图1表示信号调频率和频谱熵的关系曲线，由图中可以看出的调频率越趋近于0，熵越小，当处于零域时，信号频谱的熵达到最小。这说明，频谱熵的大小对于调频率的大小具有明显的指示作用，因此，可以根据信号频谱熵的变化趋势来估计调频率。

图1 调频率与信号频谱的熵的关系曲线

2 SEM算法流程

2.1 建立相位补偿因子

根据信号调频率与频谱熵的关系，利用熵最小化的方法对信号的调频率进行估计。在估计过程中，首先建立相位补偿因子

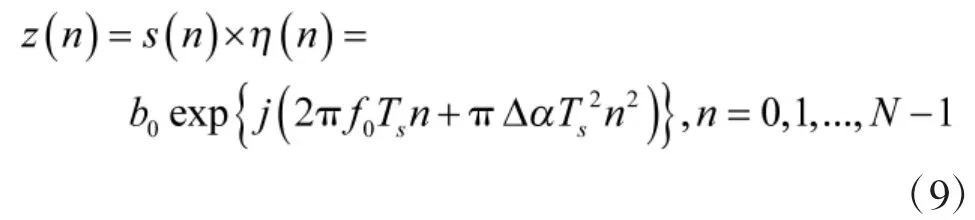
2.2 的估值搜索

为了得到全局最小熵，本文采用一维搜索的方

为了平衡估计精度和计算复杂度，本文采用两级搜索的策略:

其中，

仿真分析表明，选取合适的搜索步长λ，式（10）～式（12）描述的迭代搜索可以在少于5次的迭代之后使得熵达到全局最优。由于牛顿迭代算法对于初值比较敏感，而初值的选择与扫描点数M或者步长λ直接相关，合理地选择扫描间隔和扫描范围，可以充分发挥牛顿迭代算法收敛的有效性。

本文提出的SEM算法所需的计算量为频谱熵的扫描搜索和迭代搜索，其中，第1步中的扫描搜索，假设扫描点数为M，信号长度为N，相应的计算复杂度为O（MN log2N），第2步中每次迭代搜索需要2次FFT和2N次复乘，计算复杂度为O（2N log2N），假设迭代次数为K，则迭代搜索的计算复杂度为O（2KN log2N），一般有K＜＜M，因此，EM算法的计算复杂度为O（MN log2N），相比于一般的时频分析方法（复杂度一般为O（N3）），本文算法的复杂度较小。

为了进一步了解SEM算法的估计性能，下一节将从估计的统计特性出发，推导该算法估计的理论均值和理论方差。

3 SEM算法统计特性分析

本节讨论SEM估计方法在高斯白噪声条件下的估计性能，即SEM估计的理论均值和理论方差。为了给出严格准确的推导过程，采用一阶扰动法进行分析。

在理想非噪声条件下，式（9）的离散傅里叶变换为Z（k），其频谱熵对求偏导，有

由式（18）可知，在搜索过程中，熵存在多个极小点，如图2所示，并且频谱熵极小点具有周期性，且极小点附近的频谱熵函数具有凸函数特性，设置合理的搜索间隔，EM算法的粗扫描搜索得到的初值就会落入具有凸函数特性的最小熵对应的波谷中，再利用牛顿迭代算法就可以较快地收敛到全局最小熵点。

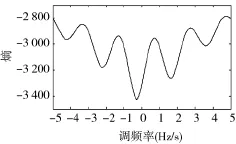
图2 熵的多极小值点示意图

特别地，对应全局最小熵的调频率估计为

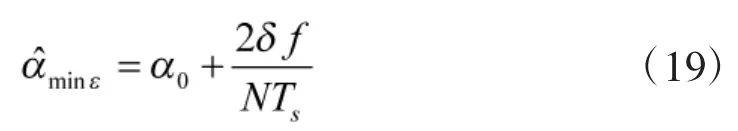
式（19）说明，EM算法对于调频率的估计是有偏估计，这一偏差与δω0直接相关。下面为了简化EM算法估计的理论方差推导的复杂度，不失一般性，设ω0=0，此时，在噪声条件下，线性调频信号的表达式为

其中，w（n）为复高斯白噪声均值为0，方差为σ02，定义信噪比（Signal-to-Noise Ratio，SNR）为

将信号r（n）与相位补偿因子相乘得到

其中

s*（n）为s（n）的共轭。

根据一阶扰动法，定义频谱熵的误差函数为

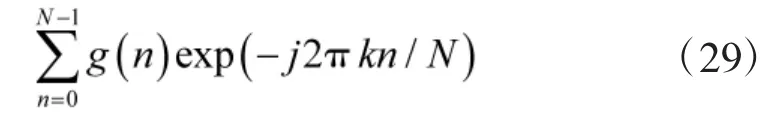
其次，对于式（27）的分母有

此时，根据误差的统计特性，估计的均值误差和均方根误差的理论表示为:

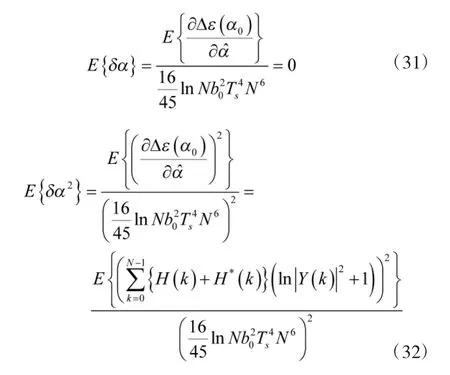
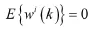
将CR下界对本文估计方法的均方误差进行归一化，可得归一化系数为

说明SEM估计方法的理论方差要小于CR下界，在估计性能上更稳定，鲁棒性更好。综上，SEM算法的调频率估计为有偏估计，估计误差δα的统计特性为:

4 仿真结果

为了说明上节关于SEM算法有偏性以及估计方差的理论结果的正确性以及算法对于实际应用的有效性，本节将SEM算法分别应用到仿真环境和实测场景条件下加以验证。仿真条件设置如下:采样频率fs=300 Hz，信号时间宽度为1 s，初始频率分别为10 Hz、10.05 Hz、10.1 Hz和10.2 Hz（δf分别为0 Hz、0.05 Hz、0.1 Hz和0.2 Hz），调频率为100 Hz/s。本文将提出的方法与调频率估计方法中经典的DPT算法进行比较。DPT是无偏估计算法，其均方根误差在大信噪比条件下逼近CR下界，其均方根误差的归一化系数为［2］

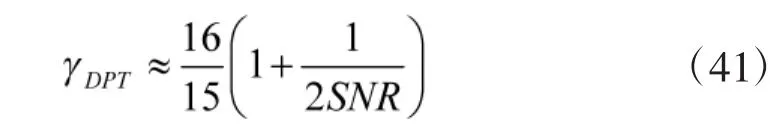
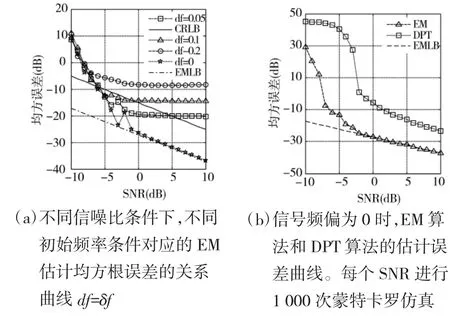
图3 误差曲线图

图3（a）表示4种δf条件下，SEM算法的估计均方误差曲线。由图中可以看出，在信噪比较高时，δf的不同直接影响EM算法的估计性能，频偏越小，EM算法的均方误差就越低，当频偏为0时，EM算法的估计误差满足理论方差式（36），说明了上节理论推导的有效性。图3（b）表示在不同信噪比下，两种方法对信号初始频率为10 Hz，δf=0的调频率估计的均方根误差曲线。可以看到，当信噪比提升至-2 dB时，本文的EM算法估计的均方根误差就达到了理论值，并且对于理论下界有着很好的逼近程度。并且，EM算法的估计均方误差要比DPT算法的估计误差低12 dB，也与之前的理论推导相符。

为了进一步验证方法的有效性，将本文方法运用到某C波段脉冲雷达观测高动态目标主动段的场景中。高动态目标的雷达回波信号可以建模为LFM信号。将DPT算法和本文提出的EM算法应用到脉冲雷达回波信号的径向加速度估计中。图4表示了两种算法估计目标径向加速度的误差曲线，经过统计，EM算法的估计均方根误差为0.21 m/s2，DPT算法的均方根误差为2.41 m/s2。从图中可以看到，在部分段落，两种算法都能够实现较好精度的径向加速度估计结果。但由于实际环境空间可能存在复杂噪声、杂波或者其他干扰目标，回波信号情况复杂，此时DPT算法估计的径向加速度估值误差会因复杂成分的引入而发生明显的跳变，而EM估计算法仍可以在整个测量段落保持在稳定的估计精度，说明本文提出的EM算法估计的鲁棒性和稳定性。

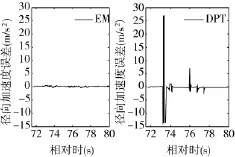
图4 两种算法的径向加速度估计误差曲线，计算段落为目标飞行相对时72 s～80 s，其中左侧图代表EM算法的估计误差，右侧图代表DPT算法的估计误差

5 结论

根据频谱熵可以有效地评价频谱的展宽程度，本文提出了一种基于最小熵准则的LFM信号调频率的参数估计方法。算法建立相位补偿因子对信号进行相位补偿滤波，通过搜索的方法得到使得滤波后信号频谱熵最小的调频率估计。在算法实现上，将牛顿迭代算法引入最小熵的搜索过程，在不降低估计精度的前提下，改善了算法的计算复杂度，简化了计算过程。本文还给出了完善的估计误差的论文分析，并发现SEM算法为有偏估计，偏差量与频域分辨率的分数部分为正比例反比例关系，而理论估计方差较CR下界低约12 dB，仿真结果证明了理论推导的正确性。利用实测数据对本文提出的EM算法进行验证，与DPT算法比较发现，SEM算法的估计性能更稳定，对于雷达实际接收回波估计的鲁棒性更好，后续将继续研究SEM算法估计偏差的修正方法，提高算法估计的准度。

［1］KELLY E J，REED I S，ROOT W L.The detection of radar echoes in noise［J］.Journal of the Society of Industrial Applied Mathematics，1960，8（2）:309-341.

［2］SHIMON P，BENJAMIN F.The discrete-polynomial-phase transform［J］.IEEE Trans.On Signal Processing，1995，43（8）:1901-1914.

［3］GABOR D.Theory of communication［J］.Proc.IEE，1946，93（3）:429-457.

［4］MARTIN W，PATRICK F.Wigner-ville spectral analysis of non-stationary processes［J］.IEEE Transactions on Acoustics Speech and Signal Processing，1985，33（6）:1461-1470.

［5］WANG Y，JIANG Y C.New time-frequency distribution based on the polynomial Wigner-ville distribution and L class of Wigner-ville distribution［J］.Signal Processing， 2010，4（2）:130-136.

［6］HUANG N E.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London.Series A:Mathematical，Physical and Engineering Sciences，1998，454（1971）:903-995.

［7］ZHANG L，SHENG J L，DUAN J.Translational motion compensation for ISAR imaging under low SNR by minimum entropy［J］.EURASIP Journal on Advances in Signal Processing，2013，8（1）:1-19.

Estimation Method of LFM Signal Chirp Rate Based on Entropy Minimization

YUAN Yuan，CAI Xiao，GUO Bei-bei
（Luoyang Electronic Equipment Testing Center，Luoyang 471003，China）

Based on the fact that the spectrum entropy decreases with the chirp rate being smaller，this paper proposes a spectrum entropy minimization（SEM）based chirp rate estimation method.A phase filter is established and the chirp rate estimation is accomplished via minimization of the spectrum entropy.In this process，a two-step search strategy is utilized.In step one，a large searching step is chosen to achieve the coarse estimation of the parameter and then Newton iterative search algorithm is used in step two to estimation the chirp rate accurately.Theoretical derivation shows that the proposed algorithm is biased，which is related to the fractional part of the initial frequency and the variance is about 12dB lower than Cramer-Rao lower bound.Simulation result proves the correctness of the derivation and the comparison with classic discrete polynomial phase transform is made.

LFM signal，minimum entropy，biased estimation，cramer-rao lower bound

TN911.7

A

1002-0640（2017）04-0091-05

2016-03-25

2016-04-10

军队预研基金资助项目（51333030103）

袁园（1990-），女，河南洛阳人，助理工程师。研究方向：通信对抗。