基于高阶滑模微分器的增广比例导引律*

杨丹丹，方洋旺，彭维仕，杨鹏飞

（1.空军工程大学航空航天工程学院，西安710038；2.武警工程大学装备工程学院，西安710086）

基于高阶滑模微分器的增广比例导引律*

杨丹丹1，方洋旺1，彭维仕2，杨鹏飞1

（1.空军工程大学航空航天工程学院，西安710038；2.武警工程大学装备工程学院，西安710086）

导引律的设计在导弹制导与控制中具有重要作用，为了解决增广比例导引中导弹-目标视线角速度和视线角加速度不易获得的问题，设计了一种基于高阶滑模微分器的增广比例导引律。首先，根据高阶滑模微分器的数学模型建立视线角速度和视线角加速度的估计模型；其次，根据视线角速度和视线角加速度的估计值，利用一种光滑无抖阵滑模微分器构造增广比例导引律。最后，通过仿真验证表明，具有滑模微分器结构的增广比例导引律导引性能良好。

增广比例导引，高阶滑模微分器，视线角速度，视线角加速度

0 引言

工程应用中，比例导引（Proportion Navigation，PN）是一种结构简单、易于实现的导引方法。在战术导弹寻的末制导飞行段，常采用比例导引方法。但在目标大机动的情况下，比例导引方法的导引性能急剧下降。因此，最优导引规律被用于解决目标大机动情况下的精确制导问题［1-2］。但是其控制规律复杂，不易于工程实现。因此，改进比例导引方法仍然是一种切实可行的导引途径。

文献［3］研究了视线角速率延迟情况下比例导引律的收敛性分析，运用李亚普诺夫函数分析延迟微分方程的收敛性并得到视线角速率的变化关系。文献［4］根据连续时间非线性预测控制方法提出了一种新的比例导引律，通过时延控制方法估计目标加速度信息。文献［5］结合滑模控制理论和比例导引律提出了一种新的鲁棒比例导引律，研究结果表明鲁棒比例导引律不仅具有很好的鲁棒性，而且在实际应用中简单易实现。文献［6］在非线性系统滑模变结构控制理论的基础上，提出一种新型滑模变结构导引律；该导引律将目标机动视为干扰，仅利用目标加速度界限的信息，在拦截过程中不需要精确的测量目标加速度，因此，该导引律对目标机动具有较强的鲁棒性。文献［8］基于扩展比例导引律提出了一种改进的方法，解决了在导弹攻击机动目标时系统状态的观测问题。

对于被动式的制导系统，一般只能提供视线角速度信号。因此，如何构造扩展比例导引律从而简单有效地从视线角速度信号中提取角加速度信号成为非常有意义的问题。文献［7，9］研究较多的是基于卡尔曼滤波估计方法，但该算法复杂、计算量大。文献［10］在分析目标运动特点的基础上，提出了一种新的基于跟踪-微分器的机动目标估计模型。该估计模型与卡尔曼滤波算法相结合，能够在动态过程完全未知的情况下估计出目标运动参数，且估计模型简单，物理意义明确，能够适应于目标的各种机动行为模式。

为解决从噪声信号中提取微分信号的问题，性能更优的微分器得到了较大发展，其中最具代表性的是Levant［10］提出的高阶滑模微分器和韩京清等［12-16］提出的非线性跟踪微分器。文献［17］根据二阶连续系统的最速控制给出了相应的高阶滑模微分器。文献［19］通过分析设计参数的选取和系统整体结构，对高阶滑模微分器进行了分析与改进，提出了高阶滑模微分器减小估计误差且更适用于工程应用的设计方法。

在文献［17，19］的基础上，本文基于高阶滑模微分器算法，构建弹目视线角速度和角加速度的估计模型；根据估计模型以期得到视线角速度和角加速度估计值，从而构造增广比例导引律。

1 增广比例导引律

假定导弹和目标均为平面内质点，忽略其动力学延迟，且导弹和目标匀速飞行［20］。导弹与目标相对运动关系如图1所示。

其中，VM和VT分别为导弹和目标的速度，R为导弹与目标之间的距离，q为视线角，σM和σT分别为导弹的弹道角和目标的航向角，ηM和ηT分别为导弹和目标的前置角，eR和eq分别为视线方向和视线法向的单位向量，eaM为垂直于导弹速度方向的单位向量，a为导弹和目标的相对加速度。

图1 导弹-目标相对运动关系图

文献［21］指出，在目标作大机动情况下，利用比例导引方法，导弹的导引性能下降。因此，引入视线角加速度构成增广比例导引律:

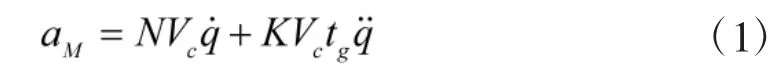
式中，N为导航比，K为视线角加速度补偿系数，Vc为导弹接近目标的速率，tg为剩余时间估计。

由式（1）知，增广比例导引律需要获得视线角速度q˙和角加速度q··。在导弹攻击目标的过程中，视线角q容易获得，视线角速度q˙和角加速度q··不易得到。因此，本文通过高阶滑模微分器来估计视线角速度q˙和角加速度q··。

2 视线角速度和角加速度模型

在文献［18］中，Levant提出了一种可精确估计任意信号微分值的高阶滑模微分器:

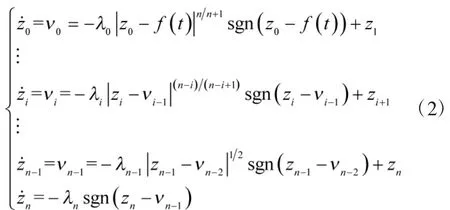
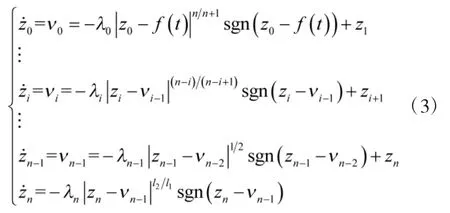
其中，f0（t）为待微分初始信号，f（t）为噪声干扰；υi为f0（t）的第i+1阶微分估计值；zi为式（3）的内部状态；l1，l2为终端吸引子设计参数，且满足l2＞0，l1＞0，l2＜l1。

类似于普通终端滑模作用原理［22］，在式（3）中，函数既能使有限时间收敛到0，又随着趋向于0的同时，也趋向于0，因而不论zn为何值均是连续的，即zn是光滑的，进而高阶滑模微分器的所有输出均是光滑的。

令式（3）的跟踪误差为:

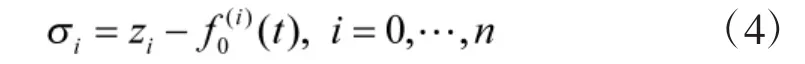
将式（4）代入式（3）可得:

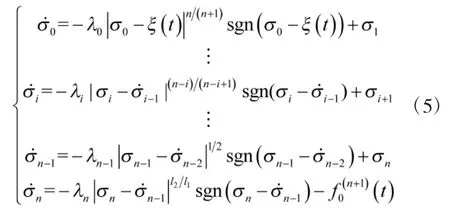
为了便于计算，令ξ（t）→0，则f（t）=q，当n=1时，得到视线角速度和角加速度的模型:

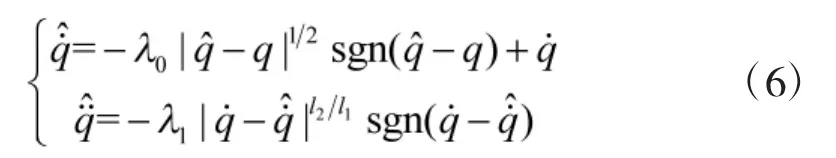
由式（5）可得估计误差为

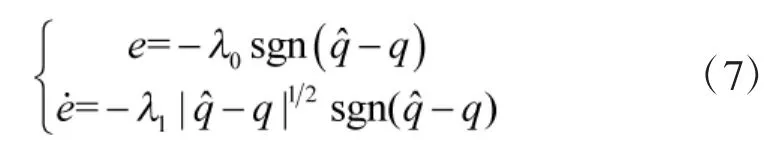
因此，在已知视线角q的情况下，可以利用式（6）、式（7）得到视线角速度估计值和视线角加速度估计值。

3 利用高阶滑模微分器构造APN

根据文献［22］，滑模微分器设计基本思想:通过附加微分方程使x（t）对（ft）进行高精度追踪，控制量u（t）用来估计。滑模微分器模型如图2，图3所示，其中f（t）为输入信号，输出u（t）为f（t）的微分信号，图3为滑模微分器算法实现图。

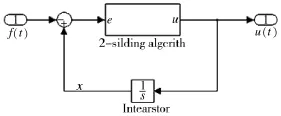
图2 滑模微分器simulink仿真模型

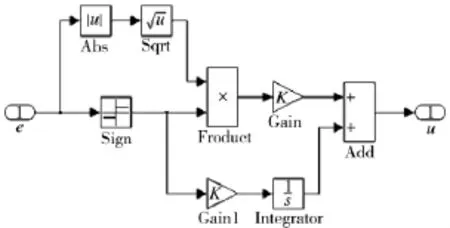
图3 滑模微分器算法实现图

当滑模微分器的输入为导弹-目视视线角q时，输出为视线角速度，当误差时，微分器可以精确观测估计视线角q。如图4所示。

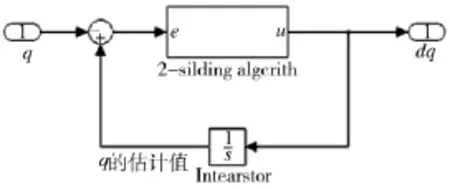
图4 角速度估计模型

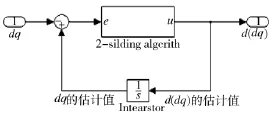
图5 角加速度估计模型

下页图6为本文设计的基于二阶滑模微分器的APN的结构图。

4 仿真算例

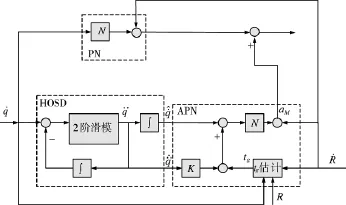
图6 基于二阶滑模微分器的APN的设计

根据式（3）搭建滑模微分器的Simulink模块如图7所示。令输入信号为sine，对该信号的估计分别如图8和图9所示。滑模微分器设计参数=500，=3 000=6 000，l1=7，l2=5。对比图8、图9和图10可以看出，改进后的滑模微分器能够很好地消除抖振，且能精确估计输入信号。

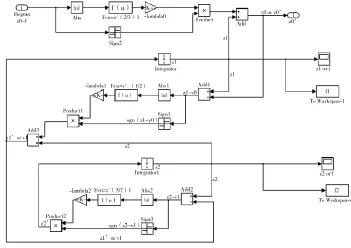
图7 滑模微分器的Simulink模块图

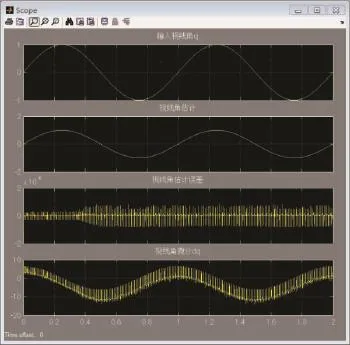
图8 一阶未改进滑模滑模微分器对sine的估计

仿真初始条件为:R0=7 km，q0=60°，σT0=0°，VT=200 m/s，VM=450 m/s，σM0=30°，目标作正旋机动。导引律参数选取如下:导航常数N=5，视线角加速度补偿系数K=1，为说明PN和APN的性能，对HOSD构造的APN进行仿真，仿真结果如图11～图13所示。

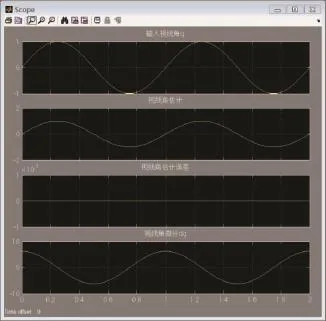
图9 二阶改进滑模微分器对sine的估计

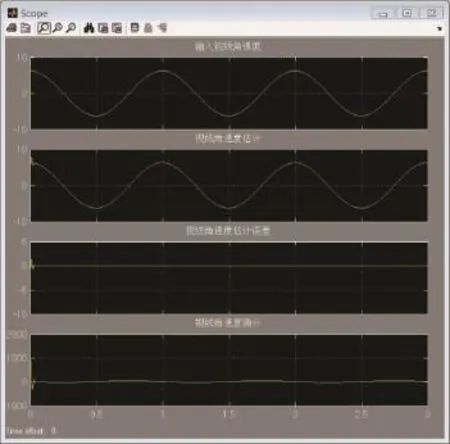
图10 二阶改进滑模微分器对sine微分的估计

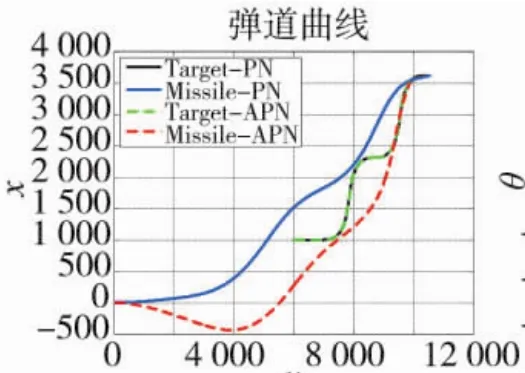
图11 弹道曲线图

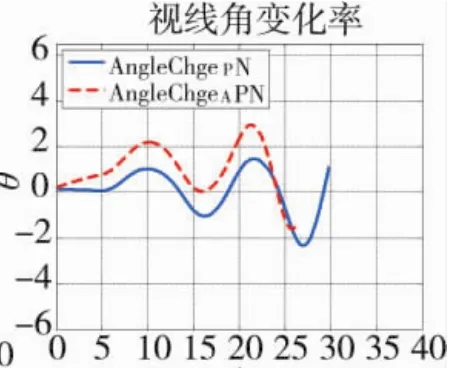
图12 视线角速率的时间历程

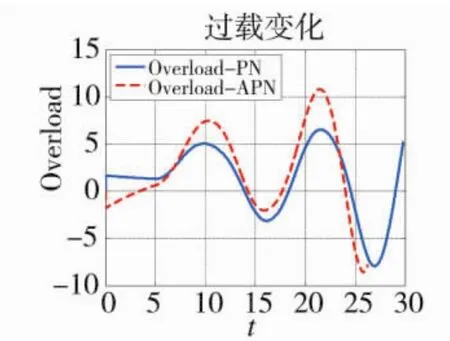
图13 过载的时间历程

分析仿真结果可得:相对于PN，APN的需用过载减小且其飞行轨迹更为平直，引入视线角加速度能够提高导引精度；APN的视线角速度的平稳性优于PN，同时由于APN的导引指令中含有目标加速度成分，APN的过载变化优于PN。对于机动目标而言，APN的命中时间明显减小且导弹具有较好的机动性能，说明引入视线角加速度的APN增强了导弹对目标的反应灵敏度。

5 结论

本文设计了一种利用高阶滑模微分器求解增广比例导引律的方法，利用高阶滑模微分器估计弹目视线角速度和角加速度，根据视线角速度和角加速度的估计值构造了增广比例导引律。仿真结果表明，由高阶滑模微分器估计得到的视线角速度和角加速度用于增广比例导引律中，有利于提高导弹对机动目标的导引性能。

［1］GEORGE M S.导弹制导与控制系统［M］.张天光，译.北京:国防工业出版社，2010.

［2］方洋旺.随机系统最优控制［M］.北京:清华大学出版社，2005:268-278.

［3］DHANANJAY N，KAI-YEW L，JIAN X X.Analysis of proportional navigation with delayed line-of-sight rate［J］.IEEE Transactions on Control Systems Technology，2013，21（1）: 247-253.

［4］TALOLE S E，GHOSH A，PHADKE S B.Proportional navigation guidance using predictive and time delay control［J］. Control Engineering Practice，2006（14）:1445-1453.

［5］SEYYED S M，GHASEM A，SOHRAB K，et al.A novel robust proportional navigation guidance law design for missile considering autopilot dynamic［J］.Transactions of the Institute of Measurement and Control，2013，35（5）:703-710.

［6］李士勇，章钱.一种新型滑模变结构导引律的研究［J］.计算机测量与控制，2009，17（8）:1541-1543.

［7］FENG D L，YANG S C，YAO Y Z，et al.Research on improved extended proportional navigation guidance［J］.Applied Mechanics and Materials Vols，2013（347-350）:980-984.

［8］CHWA D K，CHOI J Y，ANAVATTI S G.Observer—based adaptive guidance law considering target uncertainties and control loop dynamics［J］.IEEE Transactions on Control Systems Technology，2006，14（1）:112-123.

［9］SADEGHI H，POSHTAN J，MONTAZERI A.A modified proportional guidance law for homing missiles by using of nonlinear filters［C］//5th International Symposium on Mechatronics and Its Applications，2008:1-6.

［10］彭建亮，孙秀霞，董文翰，等.利用跟踪-微分器构造机动目标估计模型［J］.飞行力学，2010，28（3）:59-63.

［11］ARIE L.High-order sliding modes differentiation and output—feedback control［J］.International Journal of Control，2003，76（9／10）:924-941.

［12］ARIE L，LEONID M F.Accuracy of homogeneous sliding modes in the presence of fast actuators［J］.IEEE Trans on Automatic Control，2010，55（3）:810-814.

［13］ARIE L.Principles of 2-sliding mode design［J］.Automatica，2007，43（4）:576-586.

［14］ARIE L.Finite differences in homogeneous discontinuous control［J］.IEEE Trans on Automatic Control，2007，52（7）: 1208-1217.

［15］HUANG Y，XUE W.Active disturbance rejection control: methodology and theoretical analysis［J］.Isa Transactions，2014，53（4）:963-976.

［16］DONG X M，ZHANG P.Design and phase plane analysis of an arctangent-based tracking differentiator［J］.Control Theory&Applications，2010，27（4）:533-537.

［17］史永丽，侯朝桢.改进的非线性跟踪微分器设计［J］.控制与决策，2008，23（6）:647-650.

［18］ARIE L.Robust exact differentiation via sliding mode technique［J］.Automatica，1998，34（3）:379-384.

［19］蒲明，吴庆宪，姜长生，等.高阶滑模微分器的分析与改进［J］.控制与决策，2011，26（8）:1136-114.

［20］PAUL Z.Tactical and strategic missile guidance sixth edition［M］.America:American Institute of Aeronautics and Astronautics，Inc.2012:14-18.

［21］彭建亮，孙秀霞，董文瀚，等.利用跟踪一微分器构造增广比例导引律［J］.应用科学报，2009，27（4）:435-440.

［22］LEVANT A.High-order sliding modes differentiation and output-feedback control［J］.International Journal of Control，2003，76（9，10）:924-941.

Augmented Proportion Navigation Law Based on High Order Sliding Differentiator

YANG Dan-dan1，FANG Yang-wang1，PENG Wei-shi2，YANG Peng-fei1
（1.School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi’an 710038，China；2.School of Equipment Engineering，Armed Police Force Engineering University，Xi’an 710086，China）

The design of guidance law plays an important role important role in the missile guidance and control，a new approach of constructing augmented proportion navigation（APN），based on high order sliding differentiator（HOSD），is designed to solve the problem that it is difficult to obtain the light of sight angle velocity and acceleration.First，estimation model of Light of sight angle velocity and acceleration are established in terms of mathematical model of high order sliding differentiator. Second，augmented proportion navigation（APN）using a terse fast HOSD without chattering is constructed according to the estimation value.Finally，simulation results show that APN with HOSD has good guidance performance.

augmented proportion navigation，high order sliding differentiator，light of sight angle velocity，light of sight angle acceleration

TP273

A

1002-0640（2017）04-0058-05

2016-02-14

2016-04-28

国家安全重大基础研究基金资助项目（613271030202；15613271030202）

杨丹丹（1990-），女，陕西铜川人，硕士研究生。研究方向：网络控制。