基于CNN的高光谱影像空谱分类方法

孙 笛，车昇昆，段渭超，蒋庆仙

1.西安测绘研究所，陕西 西安，710054;

2.地理信息工程国家重点实验室，陕西 西安，710054;

3.68029部队，甘肃 兰州，730020

1 引 言

随着高光谱遥感技术的不断发展，人们可以获得越来越多、越来越可靠的高光谱影像数据，从而对高光谱影像数据所蕴含的丰富信息进行充分的挖掘利用也就更加紧迫。高光谱影像地物分类则是开展各类应用的重要环节之一，因此，高光谱影像地物分类识别得到了广泛的研究，但高光谱影像分类仍面临高维和小样本的挑战。

国内外专家学者为解决高光谱遥感影像分类问题，引入了最近邻[1]、支持向量机[2](support vectormachine，SVM)、稀疏表达[3]等分类器。 但在不进行特征提取的情况下，传统分类器很难在高光谱影像分类中取得理想结果。深度学习能够提取更加抽象的特征，进而获得更高的分类精度，近年来已经被成功用于目标识别、图像理解、机器翻译等不同领域。深度学习为高光谱影像分类识别提供了一种新的思路和途径，堆栈式自编码器[4]作为一种简单有效的深度学习方法，最早被用于高光谱影像分类。近年来，卷积神经网络也被引入到高光谱影像分类中，文献[5]设计了一种1D-CNN模型，利用光谱特征对高光谱影像进行分类，取得了优于SVM的分类结果。高光谱影像能够提供丰富的光谱和空间信息，近年来研究表明充分利用空间信息进行高光谱影像分类能够有效提高分类精度，而1D-CNN模型仅仅利用光谱信息进行分类，没有充分利用高光谱影像提供的空间信息。文献[6]利用2D-CNN模型，提取高光谱影像空间特征，并与光谱特征进行结合取得了较好的分类效果。但该方法需要事先对高光谱影像进行降维处理，且光谱和空间特征是分别提取。目前深度学习方法已经被广泛用于高光谱影像分类，且在标注样本足够的情况下能够取得优于传统分类器(如SVM)的分类精度，但基于深度学习的高光谱影像分类仍然面临小样本分类的挑战。

高光谱的不同波段影像是高度相关的，且可以被看作不同的特征映射。本文设计了一种改进的CNN模型用于高光谱影像分类，该模型直接将高光谱数据立方体作为CNN的输入，不需要事先降维度处理，能够充分从数据中挖掘光谱和空间特征，因此，即使在标注样本数量有限的情况下，也能够取得较传统方法更好的分类效果。

2 基于CNN的高光谱影像分类

CNN是一种由若干交替的卷积层和池化层组成的深度神经网络模型，已经被广泛应用于图像分类识别领域。CNN具有很高的非线性拟合能力，可以保留输入的邻域关系和空间局部性。因此，CNN非常适合对高维和非线性的高光谱数据立方体进行分析。本文设计的CNN结构如图1所示，其中包括1层卷积层、1层池化层和3层全连接层。

图1 CNN结构图

通常来说，神经网络层数越多，对非线性函数的拟合能力越强。但层数越多，需要优化的参数就越多，需要标注的训练数据也就越多。然而，高光谱影像分类标准样本费时费力，且CNN卷积层的层数受输入高光谱数据立方体对应空间大小的限制。本文输入高光谱数据立方体大小为9×9×B，其中9×9为以输入样本为中心的邻域区域的大小，B为高光谱影像波段数。综合考虑以上因素，本文采用1层卷积层来提取高光谱影像的空谱特征;采用1层池化层来减少参数数量;并采用3层全连接层来保证CNN网络的非线性拟合能力。

2.1 卷积层

CNN的权值共享和稀疏连接网络结构使之更类似于生物神经网络，降低了网络模型的复杂度，减少了权值的数量。卷积层可以定义为：

其中，*表示卷积操作;h表示输入的特征映射，也就是高光谱数据立方体;W1和b1分别表示卷积核和偏置;h1表示输出的特征映射;g(·)表示激活函数。CNN网络结构中通常会使用多个卷积核，以保证特征提取的多样性，但考虑到高光谱影像标注样本较少，且高光谱不同波段间具有高度的相关性，因此，本文设置卷积层输出特征映射数为B1(B1＜B)以减少网络参数。

2.2 池化层

池化层的输入为上一个卷积层输出的特征映射，主要作用是提供了很强的鲁棒性，并减少了参数的数量，防止了过拟合现象的发生。池化层可以定义为：

其中，h1为卷积层输出的特征映射;h2为经过池化操作的特征映射;down(·)为下采样函数，g(·)为激活函数。

2.3 全连接层

经过池化操作的特征映射需要展平，与全连接层相连，3层全连接层可以定义为：

其中，hl为全连接层输入;hl+1为输出;Wl和bl分别为权重和偏置;g(·)为激活函数。全连接层主要用于提取更加抽象的特征，以提高分类精度。

2.4 分类流程

基于CNN的高光谱分类流程主要包含采用训练数据对CNN网络进行训练，当网络充分训练后，将测试样本输入到网络，得到预测的类别标签，并与已知类别标签进行比较，得到总体分类精度。本文CNN网络的训练与传统神经网络的训练相似，包含前向传播和反向传播两个过程。前向传播就是输入数据经过网络得到输出，根据输出和已知标签计算损失函数。反向传播就是根据损失函数更新相应参数，以使损失函数最小。本文采用分批随机梯度下降法对CNN网络进行训练。

3 实 验

为验证本文算法的有效性，选取了Pavia大学和Pavia中心两组高光谱影像数据进行实验。实验软件环境为Ubuntu16.04，实验硬件环境为：内存 32G、显卡为 GTX970M、处理器为 i7-5700HQ。 CNN、1D-CNN、PCA(principle component analysis)+CNN采用Tensorflow开源库实现，SVM采用Scikit-learn开源库实现。

3.1 实验数据

Pavia大学高光谱影像数据，是由ROSIS(reflective optics system imaging spectrometer)传感器在2003年获取的，该影像的成像区域为意大利Pavia大学及其周围市区。原始的ROSIS数据包含115个波段，在试验中，去除受噪声影响严重的波段，使用剩余的103个波段的数据。数据具有610行、340列，空间分辨率为1.3m，影像范围内具有9个类别的42776个样本像元，对应训练样本个数和测试样本个数见表1。

表1 Pavia大学数据训练和测试样本

Pavia中心高光谱影像数据，是由ROSIS传感器在2003年获取的，该影像的成像区域为意大利Pavia市中心区域。原始的ROSIS数据包含115个波段，在试验中，去除受噪声影响严重的波段，选取了102个波段的数据。该数据原始影像大小为1096×1096，去除381列空白数据，因此，影像大小为1096×715，空间分辨率为1.3m，影像范围内具有9个类别的148152个样本像元，对应训练样本个数和测试样本个数见表2。

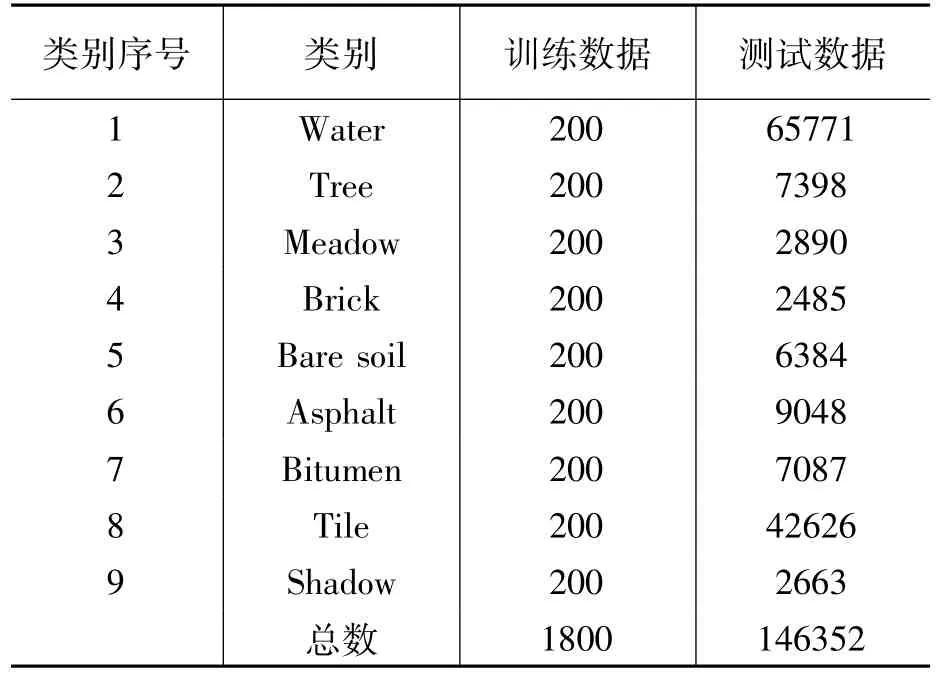
表2 Pavia中心数据训练和测试样本

3.2 网络参数设置

本文CNN用于对Pavia大学和Pavia中心高光谱数据进行分类的网络结构见表3。

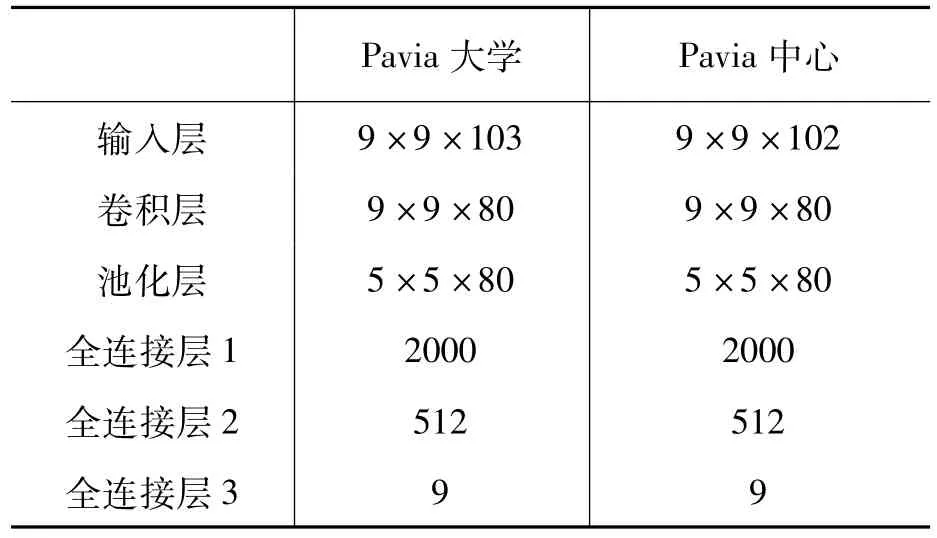
表3 网络结构

本文采用分批随机梯度下降算法对CNN网络进行优化，其中批尺寸为50，即每批输入50个样本进行训练。训练时期数为200(一个训练时期为所有训练样本完成一个正向传播和一个反向传播)。卷积核大小均为3×3×3，因此，卷积层需要对原始输入进行补边处理，补边大小为1(即9×9大小的输入，补边为11×11)，卷积核个数为80，卷积层的步长为1。激活函数采用ReLu(rectified linear units)，该激活函数能够有效抑制梯度消失。池化层采用最大池化，学习率根据经验设置为0.001，其中权重和偏置参数初始化从-0.001到0.001区间均匀随机取值。

3.3 分类结果分析

将本文算法分别与SVM、1D-CNN和PCA+CNN等现有算法进行对比。其中Pavia大学数据和Pavia中心数据对应的各个地物类别分类精度和总体分类精度分别见表4和表5。Spec-SVM为直接采用光谱特征作为SVM输入的分类结果。根据表4和表5的实验结果可知，1D-CNN仅仅利用光谱特征进行分类，分类精度略低于SVM;PCA+CNN能够利用空间信息，分类精度优于SVM和1D-CNN，但该方法需要使用PCA对高光谱影像进行降维处理，且空间信息和光谱信息是分别提取的，因此，不能有效利用高光谱影像提供的空谱信息;而本文CNN网络不需要进行降维处理，直接以高光谱数据立方体作为网络输入，能够更加有效地利用高光谱影像的空谱信息，因此，其分类精度优于SVM、1D-CNN和PCA+CNN。

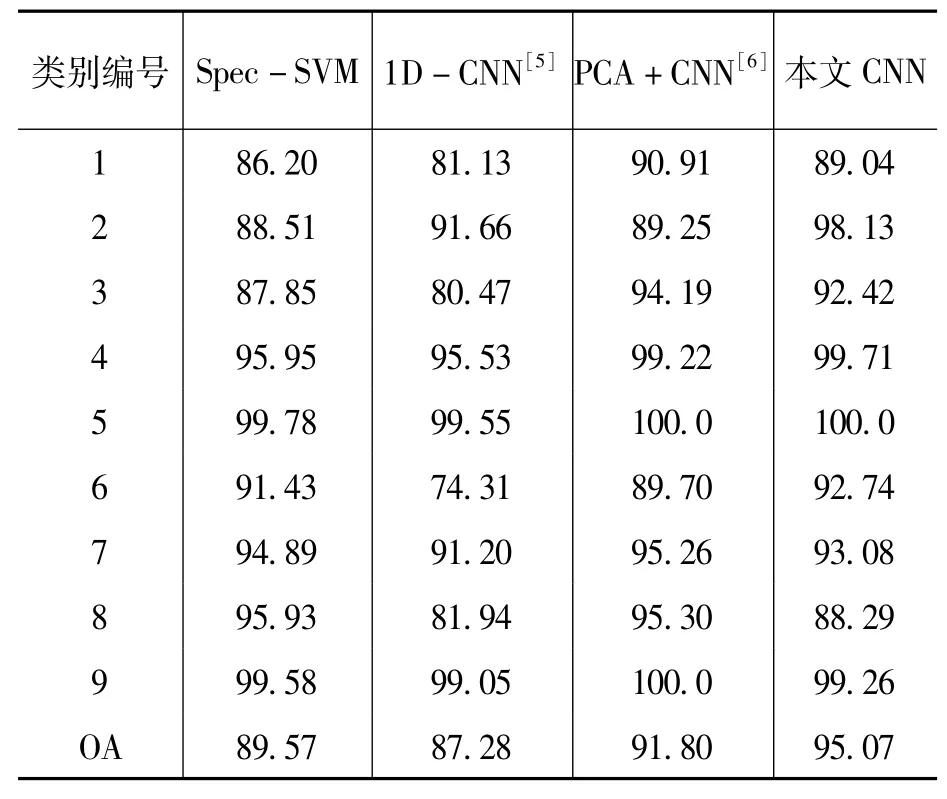
表4 Pavia大学数据分类精度

表5 Pavia中心数据分类精度

Pavia大学数据和Pavia中心数据各方法分类图如图2和图3所示。其中，图2(a)和图3(a)为已知分类图。由图可知使用本文CNN获得的分类图噪声比 SVM、1D-CNN和 PCA+CNN更少。

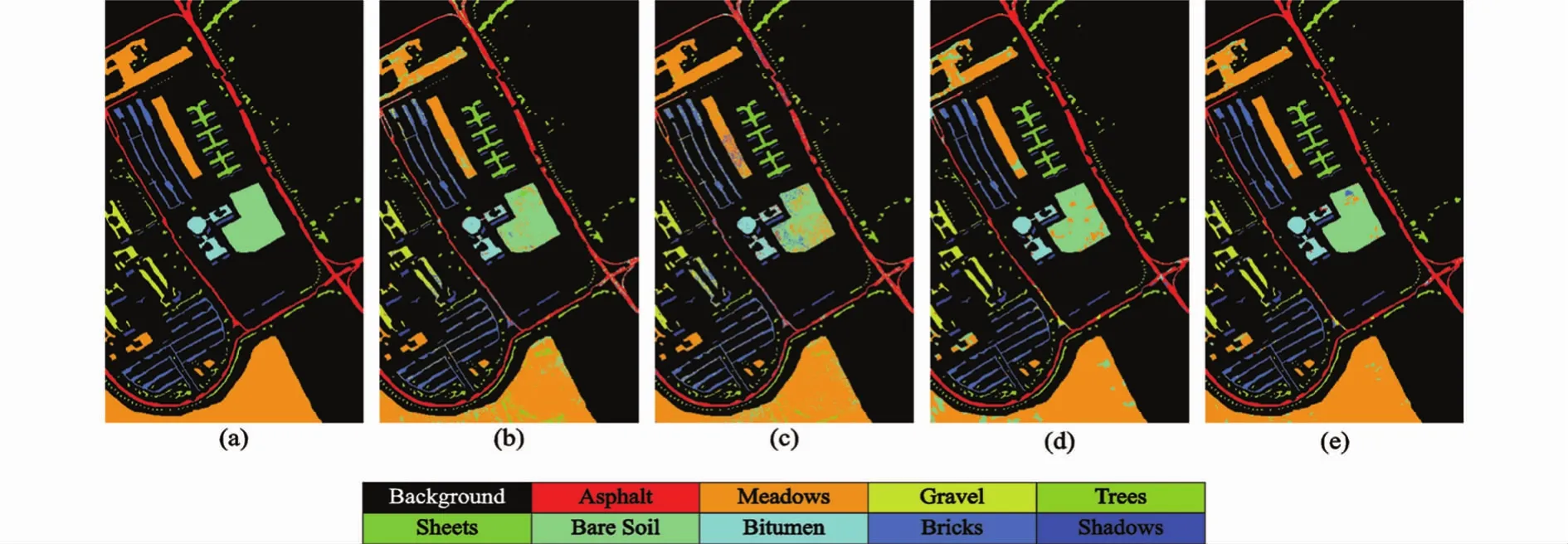
图2 (a)已知分类图

表6给出了各方法的训练和测试计算时间。其中，Spec-SVM核函数和惩罚系数参数采用交叉验证的方法需要选取，训练时需要大量时间寻找最优参数。CNN算法采用GPU并行计算，而SVM仅仅使用CPU进行计算，因此基于SVM的方法测试时间相比于基于CNN的方法要慢。1D-CNN需要较多的训练时间才能收敛，因此，训练时间最长，但由于参数最少，使得测试时间最短。而PCA+CNN由于使用PCA进行降维处理，参数要明显少于本文CNN网络，因此，训练和测试时间相对于本文CNN均较快。本文方法训练和测试耗时适中，但有效提高了分类精度。

图3 (a)已知分类图

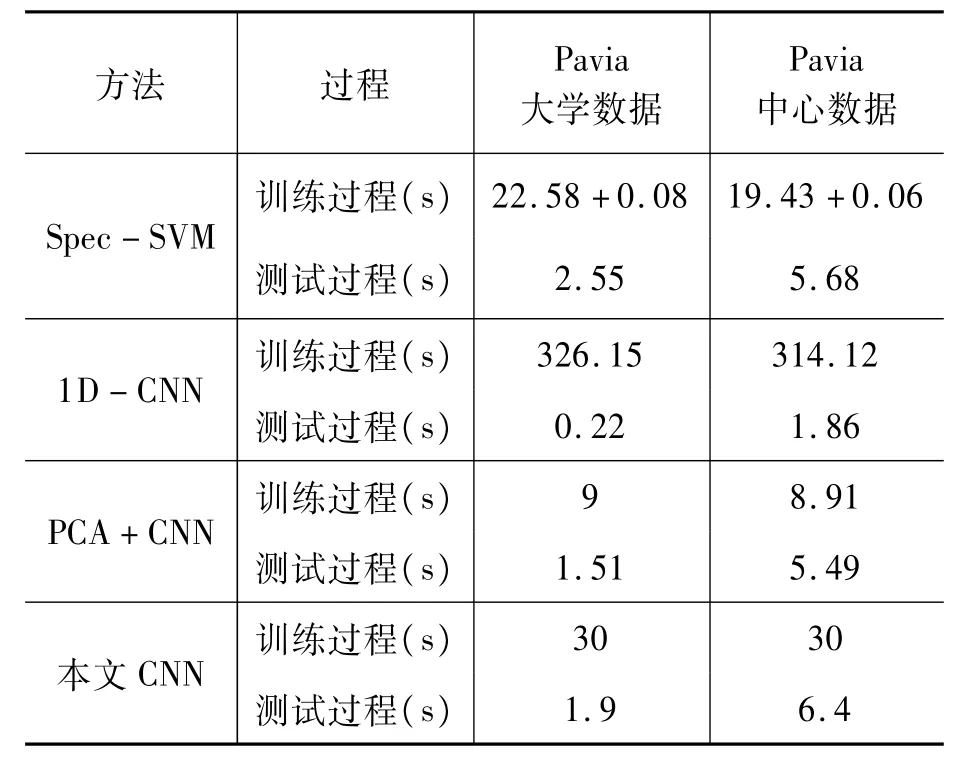
表6 训练和测试计算时间统计

4 结 语

深度学习能够在中大规模数据上取得较好分类效果，而高光谱分类标注样本有限，通常属于小样本分类，因此，深度学习方法用于高光谱影像分类仍面临小样本的挑战。本文设计了一种CNN网络用于高光谱影像分类的方法，该方法不需要降维等预处理，直接以高光谱数据立方体为输入，能够更好地利用高光谱影像提供的丰富的空谱信息，且使用较少的训练样本(每类200个训练，剩余测试)能够取得较 SVM、1D-CNN和 PCA+CNN更好的分类效果。

[1]黄鸿，郑新磊.加权空-谱与最近邻分类器相结合的高光谱图像分类[J].光学精密工程，2016，24(4)：873-881.

[2]Camps-Valls G，Bruzzone L.Kernel-Based Methods for Hyperspectral Image Classification[J].IEEE Transactions on Geoscience&Remote Sensing，2005，43(6)：1351-1362.

[3]唐中奇，付光远，陈进等.基于多尺度分割的高光谱图像稀疏表示与分类[J].光学精密工程，2015，23(9)：2708-2714.

[4]CHEN Y S，LIN Z H，ZHAO X，et al.Deep Learningbased Classification of Hyperspectral Data[J].IEEE Journal of Selected Topics in Applied Earth Observations&Remote Sensing，2014，7(6)：2094-2107.

[5]Hu W，Huang Y，Wei L，et al.Deep Convolutional Neural Networks for Hyperspectral Image Classification[J].Journal of Sensors，2015，2015(2)：1-12.

[6]Yue J，ZhaoW，Mao S，et al.Spectral-spatial Classification of Hyperspectral Images Using Deep Convolutional Neural Networks[J].Remote Sensing Letters，2015，6(6)：468-477.