利用DBN与LBP的多光谱遥感图像分类

刘松林，李新涛，巩丹超，郭 丽

1.西安测绘研究所，陕西 西安，710054;

2.地理信息工程国家重点实验室，陕西 西安，710054;

3.测绘信息技术总站，陕西 西安，710054

1 引 言

遥感图像分类是对图像中每个像素划分类别的过程，它在地理信息数据库更新、城市规划、灾情检测等方面具有重要的研究意义[1]。随着遥感技术的不断进步，可以获得的遥感图像种类越来越多，地物的光谱和纹理等特征也越来越丰富。图像中大量细节的出现和地物光谱特征的复杂化，导致了传统统计分类方法的准确率降低。

基于此，研究者将机器学习算法如神经网络(neural network，NN)、支持向量机(support vector machine，SVM)等[2]应用于图像分类，并且在分类过程中加入光谱或纹理等特征。然而SVM和NN均为浅层学习算法，难以有效地表达复杂函数[2]，所以随着训练集数量和多样性的增加，浅层模型逐渐无法适应。而由多层非线性映射层组成的深度学习网络拥有强大的函数表达能力，在图像和场景分类等应用中具有很好的效果[3-8]。

深度学习可以看作是神经网络的发展，它模拟大脑的学习过程，通过对输入数据从低层到高层渐进地进行特征提取，最终形成适合分类处理的特征。2006年，Hinton等采用深度网络模型实现了数据的降维和分类[3]，并指出深层的网络结构可以学习到数据更为本质的特征，分类性能更强。当前，主要的深度学习网络有深度置信网络(deep belief network，DBN)和卷积神经网络(convolutional neural network，CNN)等。文献[4]将SAR图像相关矩阵的对角线元素作为DBN的输入，进行SAR图像分类，取得了优于SVM的分类效果。文献[5]首先提取图像的空间和光谱特征，并将其首尾相接形成空谱联合特征，然后采用DBN对该联合特征进行协同解译，获得了很好的解译效果，尤其是对于道路和楼房两类地物有明显的改善。文献[6]综合利用图像的光谱和纹理特征，有效提高了基于DBN的高分辨率遥感图像的分类精度。针对由于数据量小而导致的遥感图像场景分类精度不足的问题，文献[7]融合轮廓波变换和CNN，设计了一种基于多尺度CNN的分类方法，提高了遥感图像场景分类结果。文献[8]首先使用PCA Saliency检测图像中的显著性区域，然后利用CNN和SVM实现了高分辨率遥感图像的场景分类。

受上述文献启发，本文通过在图像中提取局部二值模式(local binary pattern，LBP)纹理特征[9，10]，设计了一种利用深度置信网络(DBN)的多光谱遥感图像分类方法。

2 DBN模型

深度置信网络由一层或多层无监督的受限波尔兹曼机(restricted Boltzmann machine，RBM)和一层有监督的反向传播(back propagation，BP)神经网络组成，其结构如图1所示。DBN的训练过程包括“预训练”和“微调”两个过程。“预训练”通过无标签样本来进行，是一种无监督方式，采用贪婪算法逐层进行优化，每层RBM的参数单独进行调整，前一层RBM训练完成后，将其输出作为下一层RBM的输入。预训练完毕后，采用有监督学习方式对最后一层的BP网络进行训练，并将网络预测输出与实际真值标签的误差逐层反向传播，对整个DBN网络的权值进行“微调”。这时可以将DBN看作是一个普通的神经网络，但与传统神经网络不同的是各层的权重是通过预训练得到，而并非随机初始化。这使得DBN能够克服传统神经网络因权值参数随机初始化而引起的局部最优解和训练时间过长的缺点[6]。

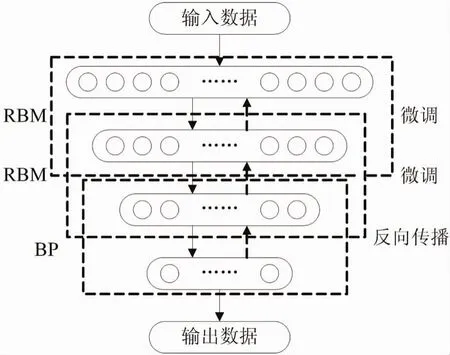
图1 DBN结构示意图

RBM本质上是一种描述对象概率分布的生成式随机神经网络模型，可以用来学习输入数据的一个概率分布。如图2所示，它包含m个可见层节点vi和n个隐藏层节点hj，其中W表示两层之间的连接权值。可见节点一般对应于观测数据，隐含节点可视为特征提取器。可见层节点与隐含层节点之间为全连接，而各层内节点之间没有连接。

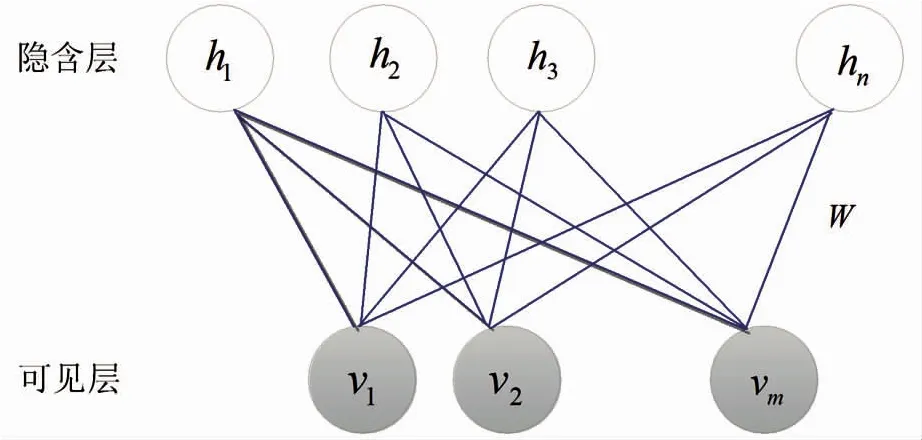
图2 RBM结构示意图

对于一组(v，h)，RBM的能量定义为：

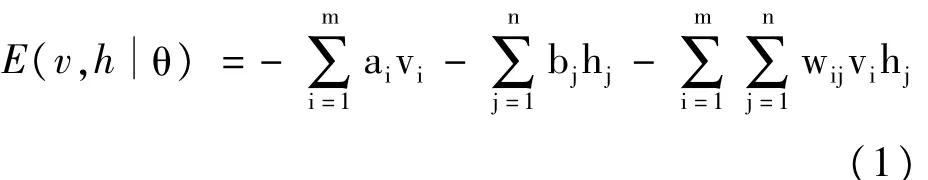
其中，Z(θ)为归一化项。在实际应用中，我们关注的是关于观测值的分布，即似然函数p(vθ)，它是联合概率的边缘分布。

由于RBM的各层内节点之间没有连接，当可见层节点的状态确定时，隐含层各节点的激活状态是彼此独立的[4]。以第j个隐含层节点为例，其激活概率如下式所示：

其中，σ(x)为sigmoid函数。同理，当隐含层节点的状态确定时，可见层节点i的激活概率为：

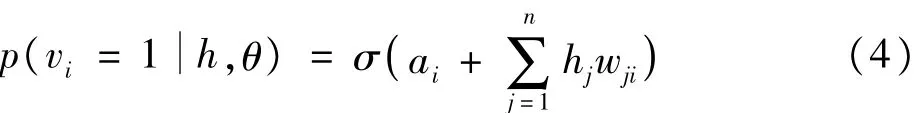
RBM采用迭代的方式进行训练，目的在于学习出参数θ，以拟合给定的数据。通过在训练数据集上求取对数似然函数的极大值可以得到参数θ，即：

其中，T为训练集中的样本数量。

根据对比散度(contrastive divergence，CD)算法的思想[11]，各参数的更新规则为：

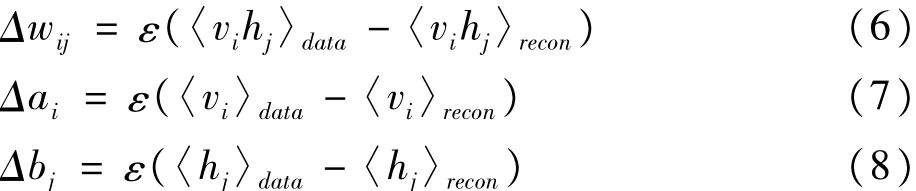
其中，ε为预训练过程的学习率;〈·〉data为训练数据集所定义的分布之上的数学期望;〈·〉recon为重构后的模型所定义的分布上的期望。

3 局部二值模式

3.1 LBP

纹理是指图像灰度局部不规则、宏观有规律的特性，其在空间上存在缓慢或者周期性的变化。局部二值模式(LBP)是一种典型的局部纹理特征描述符，它的计算效率比较高，且具有旋转和灰度不变性[12]，已经被广泛应用于地物分类和语义分割等遥感图像处理领域。

原始LBP算子是在3×3邻域内计算的，以邻域中心像素值作为基准，将邻域内8个像素值与阈值进行对比，大于基准标记为1，小于基准则标记为0，从而形成8位二进制数。将该二进制数转化成十进制，即为中心点位置的LBP特征值。特征值计算公式如下：

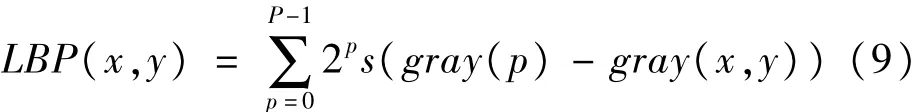
其中，gray(x，y)为中心像素灰度值;p为邻域像素序号;P为邻域点总数;s(·)为符号函数。

仅使用3×3邻域内像素进行对比，无法获得更大尺度上图像的特征信息。文献[9]对原始LBP算子进行了改进，提出了圆形邻域内的LBP特征计算方法，如图3所示。设置不同的半径R，则能够获得不同尺度上的LBP特征值。尽管在大尺度上能够得到更多的信息，但采样点的增加使得二进制数的长度相应增加，当采样点为16时，维数达到216位，实用性不强。

图3 LBP圆形模式示意图

LBP算子的邻域选择、采样点数量和特征值计算起始位置都影响着特征向量值。为了避免特征值的不稳定，文献[10]提出选择多种模式中数值最小的作为当前特征值，这种选择模式称为LBP旋转不变模式，其原理如图4所示，本文采用的旋转不变模式。

图4 LBP旋转不变模式示意图

3.2 算法具体步骤

本文算法的处理流程如图5所示。多光谱图像包括红(R)、绿(G)、蓝(B)和近红外(Nir)4个波段数据，对于一幅图像上每一个待分类的像素，假设用来计算纹理特征的邻域窗口大小取为win×win，同时假定利用该邻域提取的LBP特征维数为d。于是可以将在4个波段数据中提取的LBP特征组合为一个一维向量，维度为d×4。最后将组合后的LBP特征进行归一化，就可以输入DBN模型进行模型训练和像素分类。

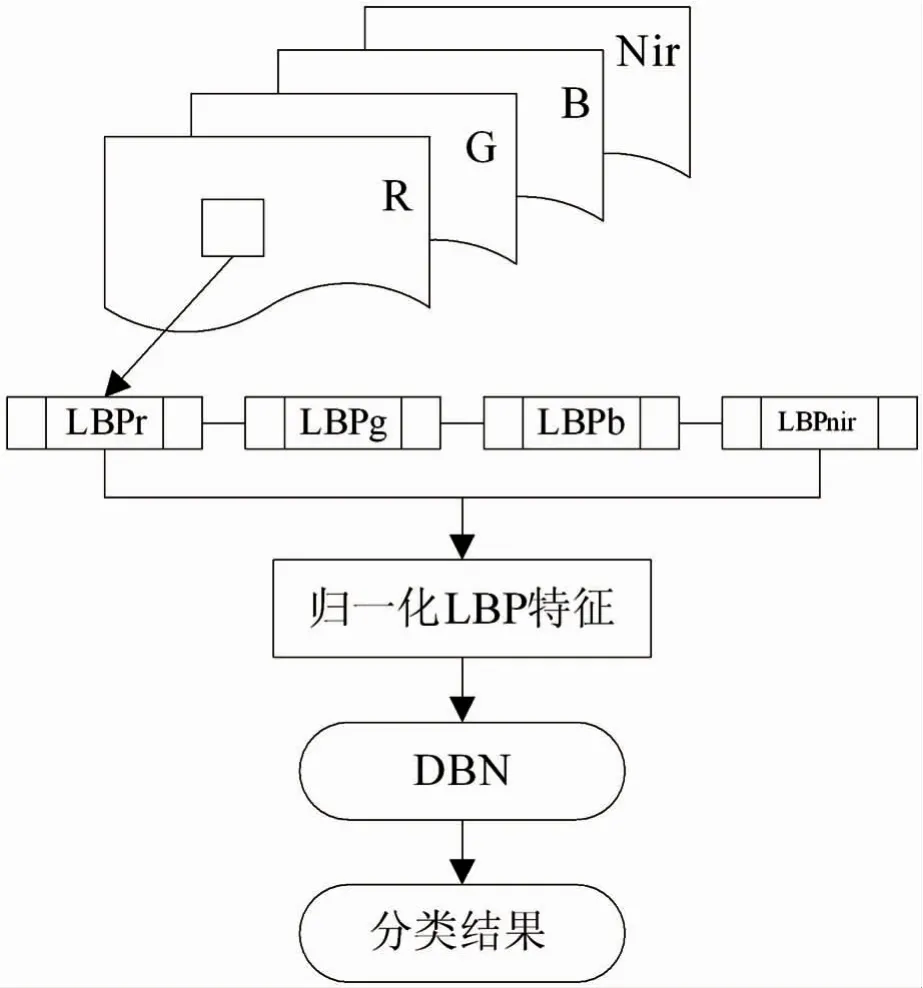
图5 基于DBN的分类方法流程图

在使用样本数据训练时，将训练数据的归一化LBP特征向量输入到第1层RBM的可见层，接下来，数据流被依次映射到各个隐含层中，这是一种逐层训练的方法。此外，DBN常采用批训练(batch 1earning)的处理方式，即每次在训练集中随机采样一定数量的样本作为一个批次进行DBN训练，每个批次完成后更新权值。

训练完成后即可进行图像像素类别预测，此时，图像中每个像素点可以用同样的方法得到同样维度的LBP特征向量，然后再通过网络的前向传播计算即可得到预测的类别。

4 实验结果及分析

为了验证算法的有效性，本文使用天绘一号卫星多光谱图像数据进行了实验。实验是在Intel E5 2.4 GHz CPU，16GB RAM的工作站上采用Matlab R2015a编程实现的。

4.1 实验数据选取及评价策略

实验数据为截取的某区域天绘一号卫星多光谱图像，尺寸为416×384，包含红、绿、蓝和近红外四个波段，图像的空间分辨率为10m，如图6所示。该区域地物类型主要包括居民区、田地、水域和道路等，其中田地根据农作物覆盖不同细分为两类，因此，对于该实验数据，地物分类总数为五类。五类地物总共标记了24163个像素点，选取其中的20%作为训练集，剩余像素作为测试集，训练集像素总数占图像总像素数的3.03%。实验中，计算LBP特征的邻域窗口win=4，每个波段的LBP特征维数d=36，于是最终得到的归一化特征向量维数为36×4=144。

图6 某区域天绘一号卫星多光谱图像

在遥感图像分类精度评价中，常利用混淆矩阵(也称为误差矩阵)，它能够反映算法分类结果与真值的误差信息，是计算算法总体精度和Kappa系数等指标的基础[4]。假定M代表混淆矩阵，其元素mij表示属于类别j但被错分到类别i的像素总数，因此，该矩阵对角线的元素值越大，分类精度越高。总体精度(overall accuracy，OA)的计算方法是，使用正确分类的像素数总和除以总的像素数。Kappa系数主要反映了分类结果与真值之间的吻合程度，它通过矩阵M的所有元素计算得到，系数值越高，算法分类精度越高，具体计算公式如下：

其中，c表示地物分类总数;N表示测试样本总数;mi+和m+i分别表示矩阵M的第i行的总和及第i列的总和。

4.2 实验参数设置

DBN的基本参数设置如下：预训练阶段和微调阶段的学习率分别为0.1和2，最小batch大小分别为80和40，epochs分别为2000和3500，权重的初始值是来自于正态分布的随机数，偏置的初始值是0。接下来，本文首先通过实验方法确定隐含层节点数。DBN的输入、输出层节点数分别为144和5，隐含层节点数在{50，75，100，125，150，175，200，225，250，275，300}内取值，计算不同取值下对应的网络重构误差，如图7所示，当隐含层节点数取175时，重构误差最小，从而确定该参数值为175。RBM的层数同样可以采用实验确定，假定各隐含层节点数相同，令层数从1变化至4，通过计算测试集的分类错误率可以得到最优RBM层数为1。

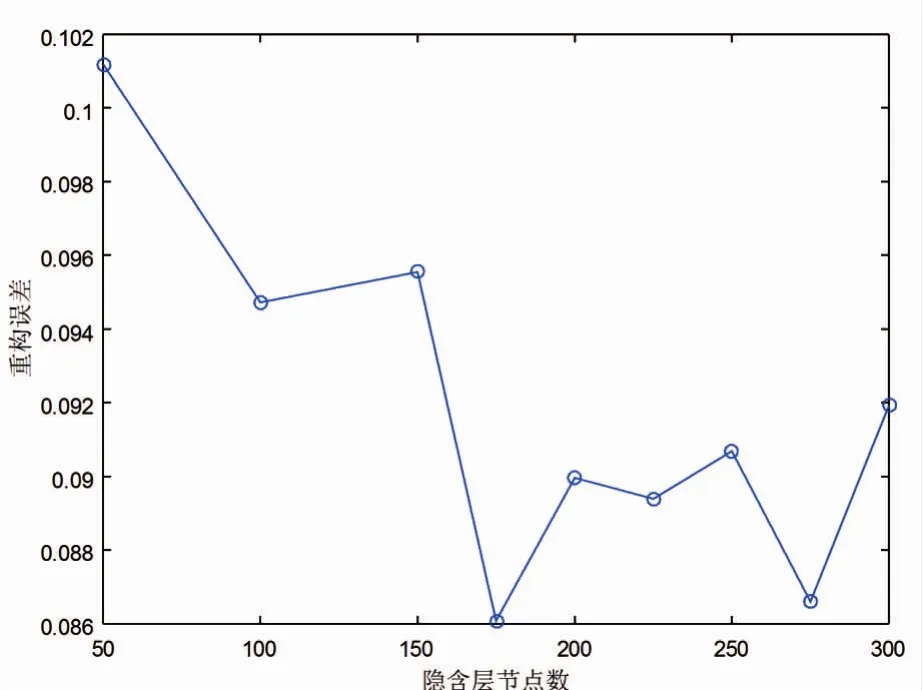
图7 不同隐含层节点数的重构误差

4.3 实验结果分析

实验一：将本文算法与SVM和NN两种方法进行对比实验，其中SVM和NN算法的最小batch大小、epochs等参数与本文算法保持一致，SVM的核函数采用径向基函数，NN采用传统的BP神经网络，它与DBN的区别在于没有RBM的预训练过程。

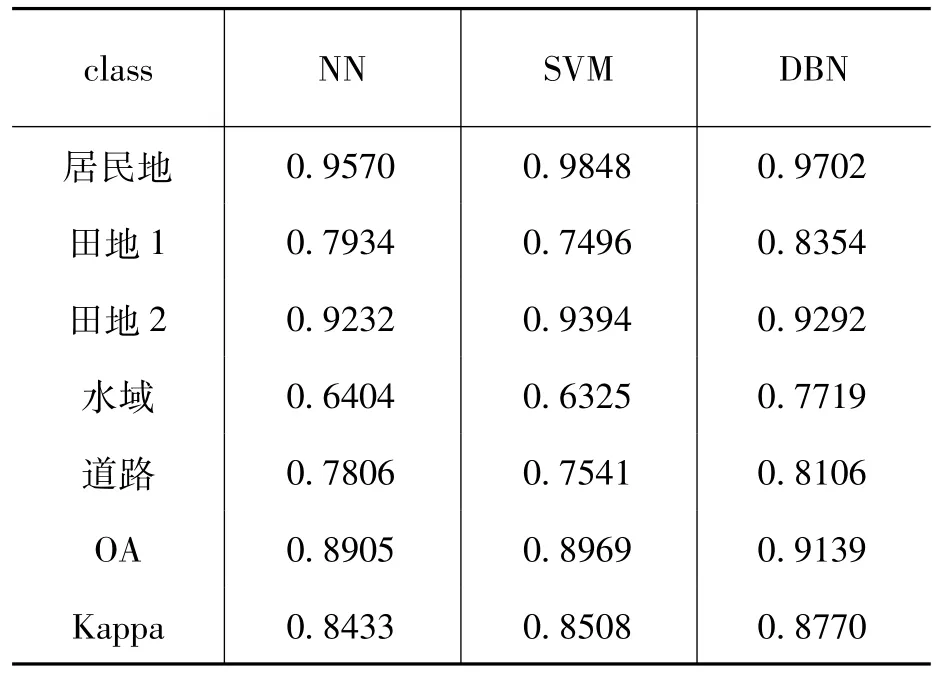
表1 不同算法分类结果比较

三种算法的定量实验结果见表1，分类结果如图8所示。从表1中可以看出，与NN方法相比，DBN在各地物类别及总体的分类精度上都有一定提升，原因在于DBN通过RBM的训练过程为NN提供了更为准确的初始权值，而在NN中，这些初始值均为随机数。因此，DBN充分利用了有监督学习(NN)和无监督学习(RBM)的优点，有效地挖掘出了多光谱图像的内在特征。与SVM方法相比，DBN方法在田地1、水域和道路几个类别上分类精度有较大幅度提高，虽然在田地2和居民地两个类别上分类精度略有下降，但DBN方法的OA和Kappa系数都优于SVM方法。

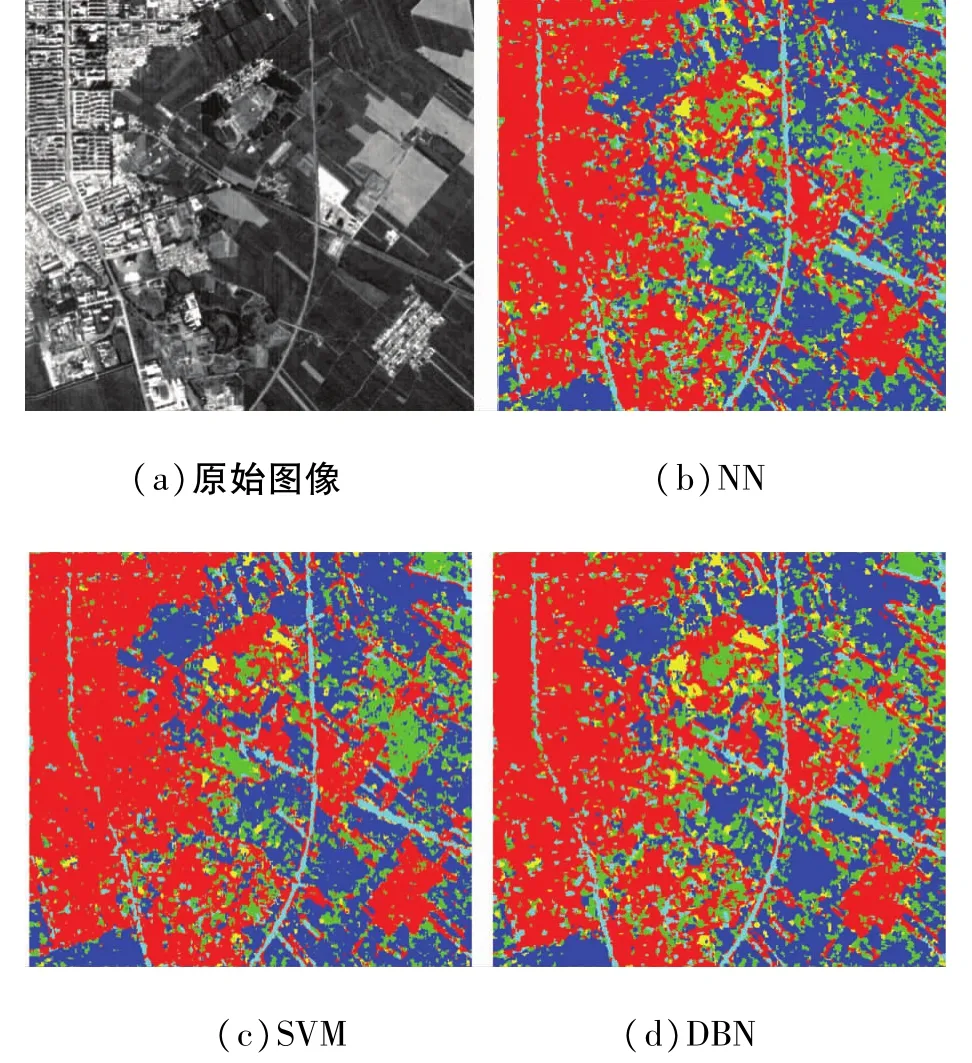
图8 分类结果示意图

下面进行实验二的测试。原始多光谱图像如图10(a)所示，尺寸为401×401，该区域地物类型主要包括居民区、田地1、田地2和道路。四类地物总共标记了32841个像素点，选取其中的20%作为训练集，剩余像素作为测试集，训练集像素总数占图像总像素数的4.08%。在该组实验中，DBN的基本参数设置如下：预训练阶段和微调阶段的学习率分别为0.1和2，最小batch大小均为6，epochs分别为2000和4000，RBM层数同样为1，权重的初始值是来自于正态分布的随机数，偏置的初始值是0。采用同样的方法确定隐含层节点数为150，此时重构误差为0.0183，如图9所示。实验结果在表2和图10(c)～(d)中给出。从表2中可以看出，本文算法在OA和Kappa系数上均优于NN和SVM算法。

图9 实验二不同隐含层节点数的重构误差

表2 实验二不同算法分类结果比较

5 结 论

本文以实现多光谱遥感图像典型地物分类为牵引，通过分析网络模型和图像纹理特征，提出了一种利用DBN与LBP特征的分类算法。首先，提取多光谱图像各波段的LBP纹理特征，并将其组合、归一化，形成DBN输入特征向量;然后，使用训练数据集对DBN网络进行训练;最后，利用训练好的DBN网络完成图像分类。实验表明，本文算法能够取得优于NN和SVM等传统算法的效果。同时也可以看出，DBN只是在NN的基础上增加了利用RBM的预训练过程，整体分类精度还有待于进一步提升。接下来，我们将对性能更加优异的卷积神经网络做进一步研究。

[1]史文中，朱长青，王昱.从遥感影像提取道路特征的方法综述与展望[J].测绘学报，2001，30(3)：257-262.

[2]周志华.机器学习[M].北京：清华大学出版社，2016.

[3]Hinton G，Osindero S，The Y.A Fast Learning Algorithm for Deep Belief Nets[J].Neural Computation，2006，18(7)：1527-1554.

[4]吕启，窦勇，牛新等.基于DBN模型的遥感图像分类[J].计算机研究与发展，2014，51(9)：1911-1918.

[5]李彤.多谱遥感影像特征提取及协同解译研究[D].哈尔滨：哈尔滨工业大学，2014.

[6]刘大伟，韩玲，韩晓勇.基于深度学习的高分辨率遥感影像分类研究[J].光学学报，2016，36(4)：0428001.

[7]许夙晖，慕晓冬，赵鹏等.利用多尺度特征与深度网络对遥感影像进行场景分类[J].测绘学报，2016，45(7)：834-840.

[8]何小飞，邹峥嵘，陶超等.联合显著性和多层卷积神经网络的高分影像场景分类[J].测绘学报，2016，45(9)：1073-1080.

[9]Ojala T，Pietikainen M，Harwood D.Performance Evaluation of Texture Measures with Classification Based on Kullback Discrimination of Distributions[C].International Conference on Pattern Recognition，IEEE，1994.

[10]Maenpaa T，Pietikainen M，Viertola J.Separating Color and Pattern Information for Color Texture Discrimination[C].16thInternational Conference on Pattern Recognition IEEE，2002.

[11]Hinton G.Training Products of Experts by Minimizing Contrastive Divergence[J].Neural Computation，2002，14(8)：1771-1800.

[12]曹云刚，王志盼，慎利等.像元与对象特征融合的高分辨率遥感影像道路中心线提取[J].测绘学报，2016，45(10)：1231-1240.