电动汽车用直驱永磁轮毂电机三维温度场分析
李昕涛,丁彬城,贾田雨,贡德鹏
(1.太原科技大学,太原 030024;2.南高齿集团,南京 210012)
0 引 言
轮毂电机直接驱动系统是由电动汽车的车轮内部安装轮毂电机驱动车轮进行同轴转动,省掉了传统汽车变速传动等一系列复杂装置,精简了汽车的机械结构,提高了电动汽车的动力管理能力以及电动汽车的传动效率[1]。一般在电动汽车的设计中,为了实现轮毂电机的高功率密度、高转矩密度,都会将轮毂电机的结构变得很紧凑,安装空间也变得很小。内部定子轮毂结构的外转子式电机,由于定子损耗所产生的热量很难通过热传导传递至轮毂电机的机壳并散发出去,进行空气冷却,导致轮毂电机的机壳内部温度升高。在汽车长时间运行之下,电机产生的损耗几乎都转化成了热能[2],引起电机各部分温度升高。温度过高时,会烧毁绕组绝缘,使永磁体高温退磁,因此电机温升的研究变得至关重要。
1 电机计算模型的确定
1.1 电机物理模型的建立
图1为轮毂电机的三维模型。

(a) 轮毂电机物理模型
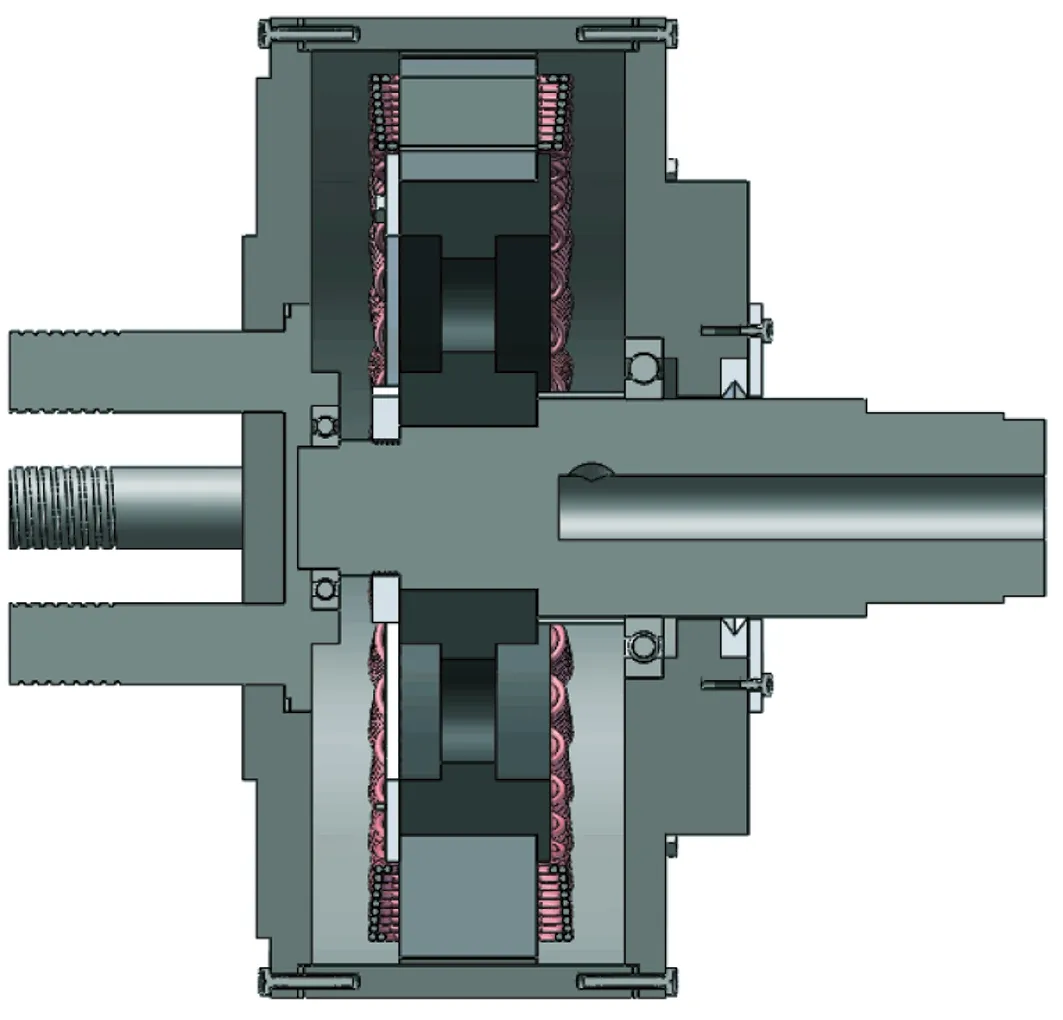
(b) 轮毂电机剖视图
电机的基本参数如表1所示。

表1 电机基本参数
1.2 轮毂电机温度场数学模型
电机中的损耗以导磁体的涡流损耗和杂散损耗、绕组线圈的损耗以及机械损耗为主,这些损耗主要存在电机的内部,由铁心和绕组为主,铁心和绕组上产生的热量一方面传导到物体表面和相邻介质,然后再经对流的方式散发到周围介质中去。根据前面的热力学理论基础,在直角坐标系下建立电机的二维热传导表达式,如下:
(1)
式中:λx,λy为电机各介质沿x,y方向上的导热系数;α为边界S2的散热系数;Te为边界S2周围介质的温度;T为电机的温度;c为比热容;q为热源;ρ为介质密度;S1为电机热流边界面;S2为电机热交换界面;λ为S1,S2边界面上的法向热传导系数;n为S1,S2边界面上的法向矢量;T1为边界S1上给定的温度。
对应的3个稳态[3]下的边界条件:
1)温度边界条件,知道物体在任意时刻的温度,如下:
T|S1=T0
(2)
式中:S1指的是物体的边界面;T0指的是在稳态求解的过程中所给定的温度。
2)热流边界条件,任何时刻边界面上已知物体的热流密度值,如下:
(3)
式中:q0指的是在S2面上的边界热流密度;λ指的是物体垂面的热传导率。
当物体面上没有发生热传导时,即此时成为绝热边界条件,此时q0=0。
3)热交换边界条件,已知边界面散热系数和附近流体温度[4],如下:
(4)
式中:Tf表示为周围物体的温度;α表示S3表面的散热系数。
α和Tf可以表示随空间或者时间的变化函数,也可以用常数来表达。
根据上式,本文在求解电机的过程中,对电机的求解区域做出等价假设[5]:
1)假设每根导线都是一样的,产生的涡流效应和铜损都是均匀分布的;
2)铁心内部与断面耗损都是均匀的,加工的槽型和尺寸大小都是一致的;
3)不考虑齿槽转矩和极弧系数对电机内部温度的影响。
针对以上假设,得出对应的边界条件如下:
a)轴向中间断面,槽中心断面为电机中的绝热面,应用于热流边界条件。
b)电机外表面、定子铁心外表面、定子端部绕组各表面为电机散热表面,应用于热交换边界条件。
2 电机温度场各物理量的确定
2.1 热载荷的确定
电机的温升主要有多损耗产生,其中机械摩擦损耗、绕组损耗和定子铁心铁耗为主要功耗,本文将这3个功耗转化成单位体积的生热率,作为电机的发热源进行求解。生热率公式:
(5)
式中:q为生热率;pw为电机相应部分损耗;V为电机对应部分体积。
本文设计中,电机定子铁心加载损耗120 W,绕组线圈加载铜耗337 W,机械损耗为75 W。将损耗代入式中,可到各部件的生热率,如表2所示。

表2 各部件的生热率表
2.2 温度场导热系数的确定
不同的物理化学材料有着其不同的导热系数,即便是同一材料在不同的温度、大气压强、环境湿度下的导热系数也会千差万别。在众多所影响的因素中,温度对材料的导热系数所产生的影响最大。针对轮毂电机中各个部件所采用不同的材料,本文分别来求导热系数。
1)绕组导热系数的确定
绕组节距在轮毂电机中取值选为1,绕线方式选择圆形散线的形式,这样的做法导致槽内排列不规律,进而导热系数的计算也比较麻烦,为了方便绕组导热系数的计算,可将端部进行简化,绕组的实际排布采用长度相等的直线来代替,并假设槽内的导线绝缘漆分布均匀,温差分布很小,且绝缘槽与铁心紧紧的结合在一起,这时的绕组可以当作一个大的导体和一个大的分布均匀绝缘体分布在周围,如图2所示。
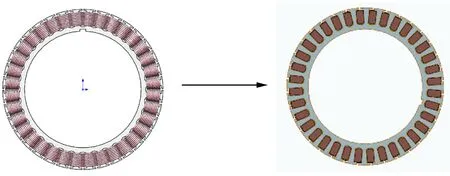
图2 等效绕组图
绕组绝缘材料的导热系数按下式可计算得到:
(6)
式中:λeq为绕组所等效的导热系数;λi为绕组中各导体的平均导热系数;δi为绕组中各导体的等效厚度。
2)内定子铁心的等效导热系数
定子铁心由多层硅钢片粘结而成,轴向导热可以看成多层平壁串联导热,导热公式:
(7)
式中:δFe为铁心厚度;λ1为硅钢片导热系数;δ0为绝缘介质的长度;λ0为绝缘介质的导热系数;KFe为铁心的叠压系数。
径向和周向的导热可以看成多层平壁并联导热,导热公式:
(8)
3)气隙等效系数
本文设计的轮毂电机为外转子电机,定转子之间通过气隙间隙来实现热交换,气隙中的空气流动方式为紊流,如果按照气隙间的对流交换则十分麻烦,部分文献采用电机定子与转子表面空气的散热系数来处理,这样存在很大的误差,并且测量气隙温度也很困难。
本文用静止流体的导热系数来等效成气隙间的空气热交换能力,将气隙中的对流换热等价为导热来分析。气隙中的空气流动可以分为层流和紊流,中间以雷诺数来区分,当转子的转速低于临界转速时,空气流动为层流,当转子的转速高于临界转速时,空气流动为紊流,气隙的等效导热系数可由以下经验公式得到:
(9)
式中:r0为定子外径;Ri为转子外径;ωφ1为转子圆周速度;δ为气隙长度;v为空气的运动粘度。
根据上述计算并结合其他研究者的实验和经验,得到电机各部件材料属性,如表3 所示。

表3 各部件散热系数表
2.3 散热系数的确定
1)机壳表面散热系数的确定
文中所设计的轮毂电机由于是直接安装在汽车轮毂的内部,所以电机的散热条件非常有限,电机上电运行的过程中,即可与电机周围的空气发生对流现象产生热传导。对流散热系数公式:
(10)
式中:α为轮毂电机表面散热系数;λ为电机周围空气导热系数;ΔTc为电机机壳内外温度差;v为流体流动粘度;L为电机轴向长度;g为重力加速度;β为气体膨胀温度系数。
2)电机内部表面散热系数的确定
电机内部各部件主要通过电机内部的空气流动来实现对流散热。对流散热计算公式[6]:
(11)
式中:δ0为部件发热表面在平静空气中的换热系数;k为气体吹动效率系数;v为电机内部气体流动速度;t为电机内部部件表面温度。
根据以上经验公式和本轮毂电机的结构,最终得到电机内部各表面的散热系数,如表4所示。

表4 各部件表面散热系数
3 轮毂电机三维温度场仿真
本文利用ANSYSWorkbench软件中的热模块,进行轮毂电机温度场的仿真,将3种损耗转化成对应部件的内部生热率,作为边界条件施加在所建模型上,设置环境温度为20℃与确定相应的散热系数后,进行模型求解。求得电机额定工作的温度分布如图3所示。
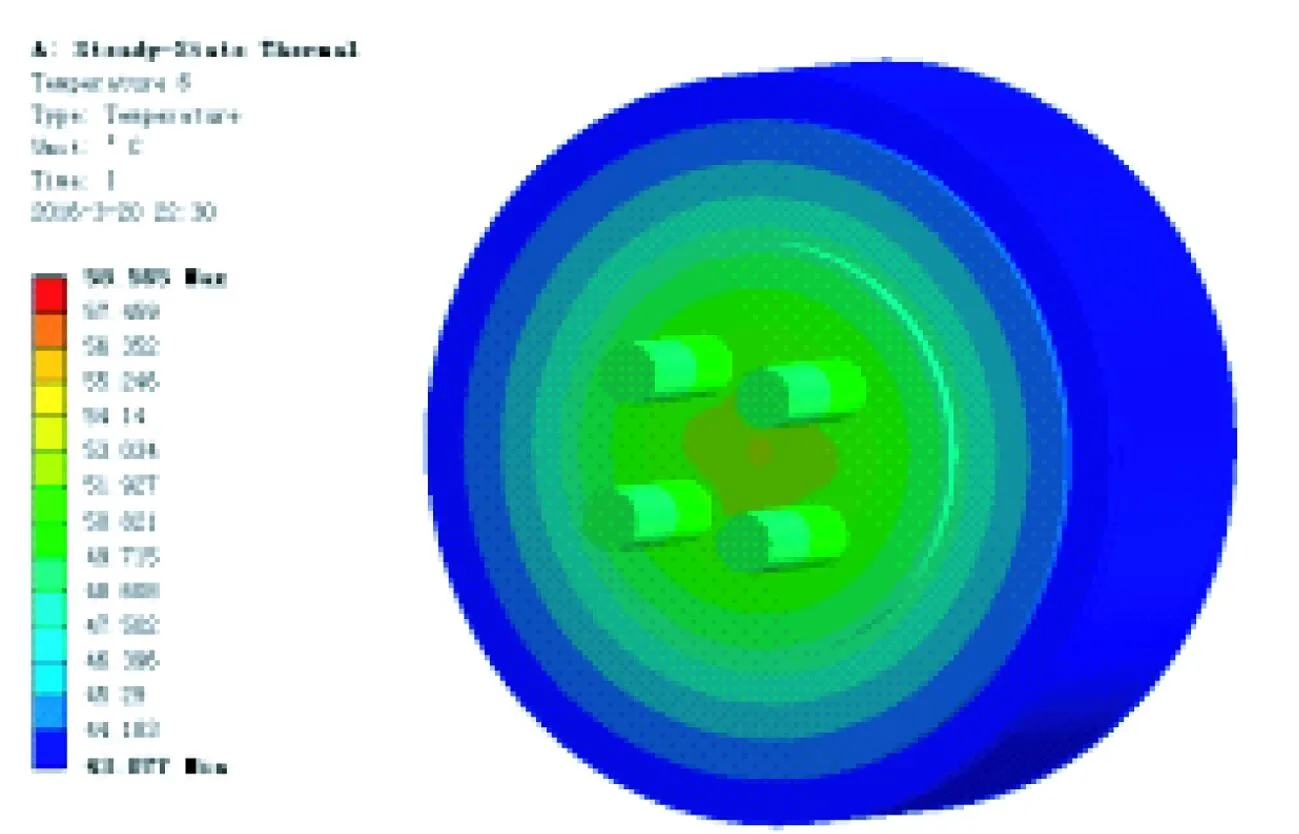


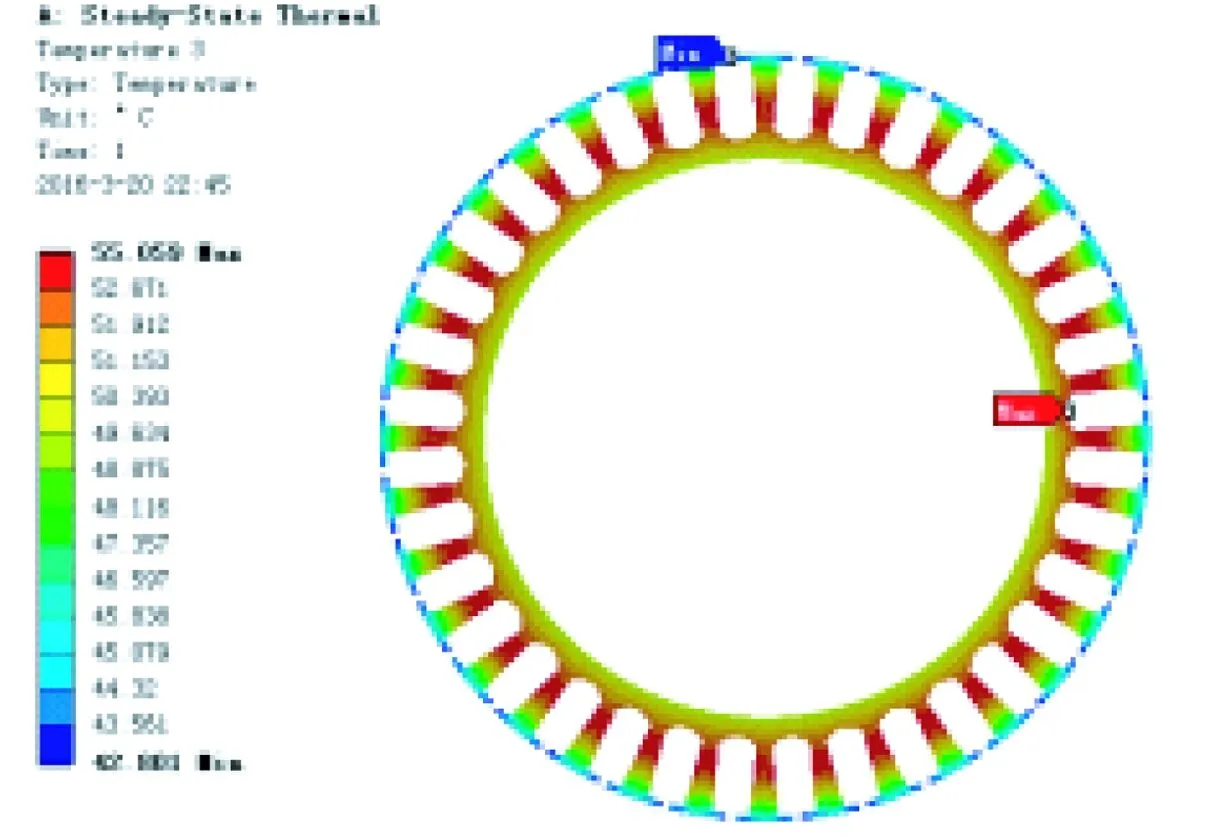
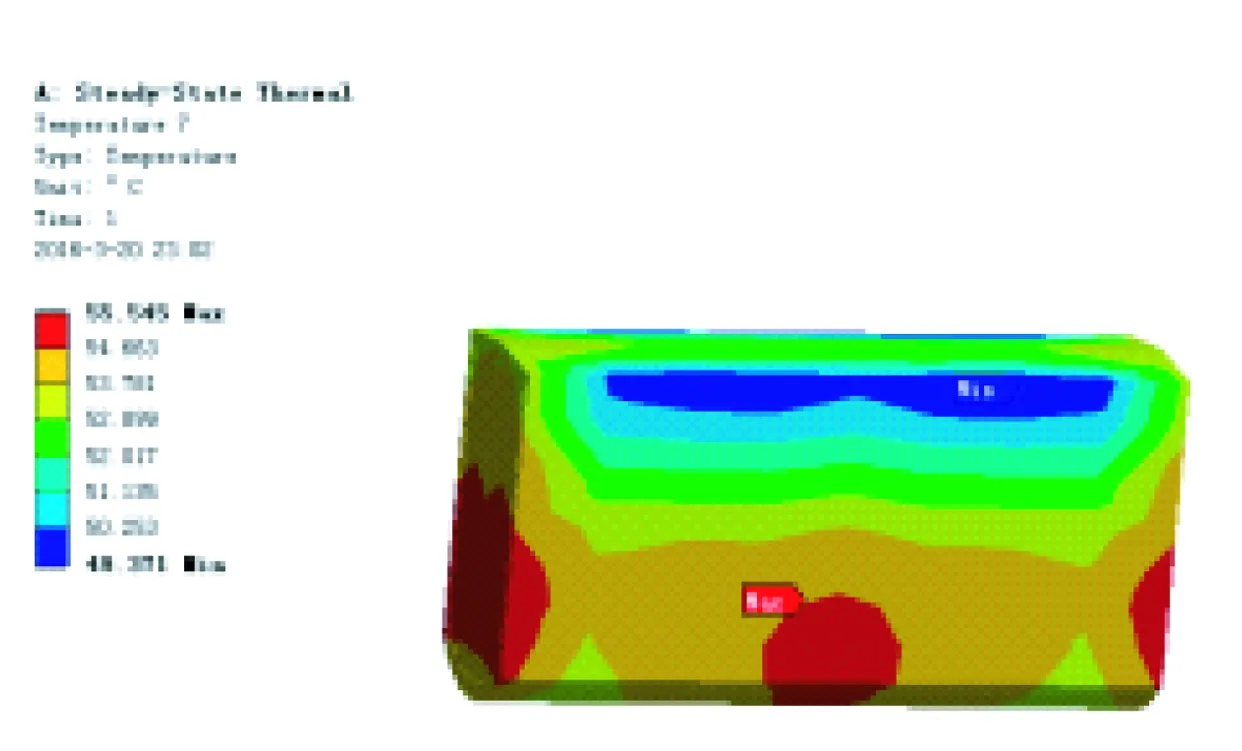

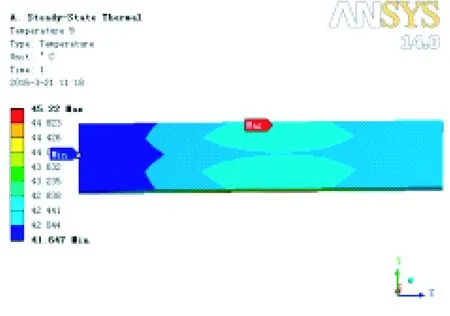
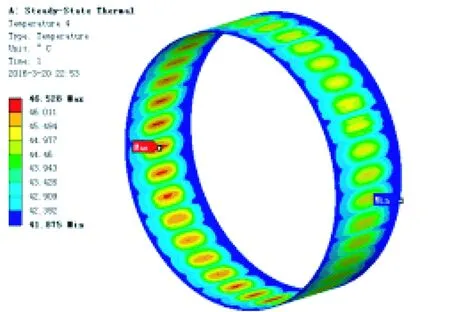
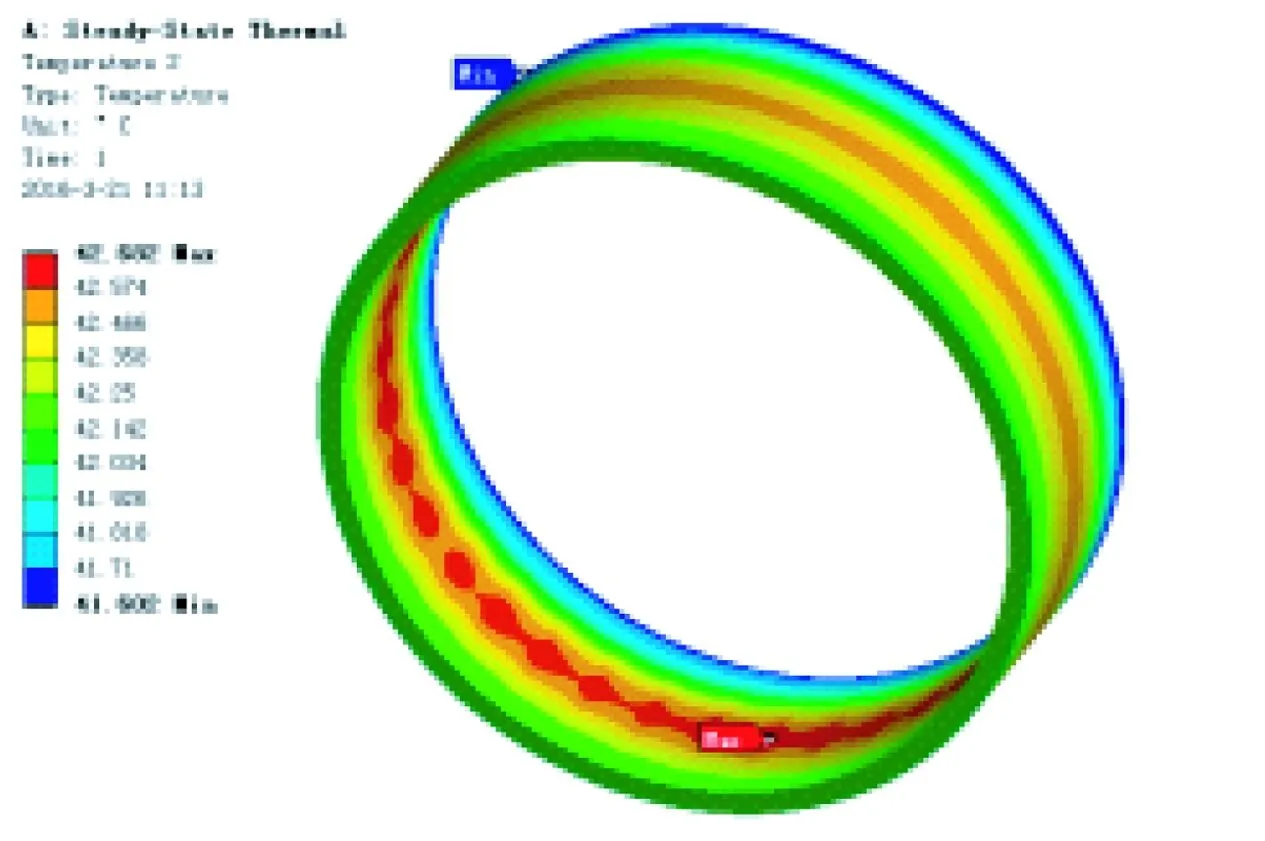
图3 Ansys温度分析图(截图)
从图3中可以看出,电机端盖的整体温度高于电机外转子外壳的温度,在端盖中心由于有轴承的机械摩擦损耗,其温度值要高于边缘温度,外转子外壳电机温度分布均匀,其温度值在43~44℃。
4 实验测试与对比
在轮毂电机性能仿真完成之后,通过对其进行实验,来检验仿真是否合理正确,如图4所示。实验用的轮毂电机,所采用的温度测量仪器为美国菲力尔红外热成像仪,它的检测范围为±250℃,可以检测到低至0.06℃的温差。可以对检测物体进行点检测,区域检测。

图4 轮毂电机
在实验室环境和光线温度都为20 ℃,相对湿度为50%的环境下,在1.5m的距离开始测量,电机尚未运行的温度如图5所示。

图5 电机在未起动时温度图(截图)
从图5中可以看到,电机在未起动时,机壳的表面平均温度为22℃,此时用来装配轮毂的4个螺栓,由于表面没有喷涂黑色油漆,表面热量散失较少,温度稍微高一些。电机温度较为均匀。
在电机运行5min之后,轮毂电机机壳中心温度开始升高,此时测得的电机温度图如图6所示。

图6 电机运行5 min之后的温度图(截图)
在电机运行10min之后,从图7可得,在轮毂电机前端盖上,轴承所在位置出现最高温度,其温度值为30.4℃,从中心到边缘温度依次降低,电机后端盖边缘处为整个电机温度最低。

图7 电机连续运行10 min时温度图(截图)
电机连续运行20min之后,最高温度上升到37.2℃。此时,在电机上划取两条测温线Li1和Li2,分别提取直线上温度,如图8所示。由图8可知,直线Li1上温度分布均匀,最大值出现在前端盖上,最小值出现在后端盖上;在直线Li2上,从端盖中心到端盖边缘,温度逐次降低,最高温度为35.79℃。

图8 电机连续运行20 min时温度分布图(截图)
在电机连续运行30min之后,电机达到稳态平衡,电机温度不在增加,如图9和图10所示,此时电机机壳最高温度为53.9℃。
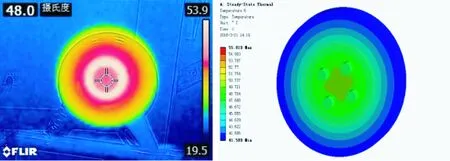
图9 电机连续运行30 min时温度图(截图)

图10 轮毂电机稳态仿真与实验对比图(截图)
从图9中可以看出,在轮毂电机轴承处的温度最高,这时的热量主要来自于轴承,整个白色的圆环状为轴承所在的位置。从图9还可以看出,最高温度出现在端盖中心位置,这时因为轴承摩擦生热,传导给轮毂法兰,法兰传导给端盖,表现出中心位置温度高,端盖边缘温度低的现象。电机端盖的最高温度出现在中心轴承处,从中心到边缘,温度逐渐降低,都呈阶梯状分布。对比图9和图10可以看到,电机转子表面温度分布均匀,仿真图和实测图电机温度分布趋势一致,验证了仿真的可靠性。
5 结 语
为解决电动汽车运行的实际需求,当轮毂电机温度过高时,严重影响了电机的稳定性的问题,本文利用ANSYS-Workbench建立3-D温度场有限元法轮毂电机模型。通过有限元计算和温升实验,并且搭建实验平台进行测试,通过温升实验的对比验证了ANSYS-Workbench建立3-D温度场有限元法轮毂电机模型的正确性。结果表明,电机温升在一个稳定可靠的范围之内,为今后继续研究轮毂电机在复杂的环境运行工况下的温度升高情况和温度场的分布奠定了基础,以及对电机的散热研究具有一定的指导价值。
[1] 褚文强,辜承林.国内外轮毂电机应用概况和发展趋势[J].微电机,2007,40(9):77-81.
[2] 葛宜舟.电动车用永磁无刷直流电机温度场分析与计算[D].合肥:中国科学技术大学,2008.
[3] 贺旭照,赵慧勇,乐嘉陵.考虑可压缩与热传导的壁面函数边界条件及其应用[J].空气动力学学报,2006,24(4):450-453.
[4] 俞清.电磁装置场路耦合法分析与温度场计算[D].沈阳:沈阳工业大学,2010.
[5] 陈薇薇.电动汽车用永磁同步电机设计及温度场分析[D].南京:南京航空航天大学,2013.
[6] 李西云.直流无刷轮毂电机损耗与内部温度场有限元分析[D].吉林:吉林大学,2013.

