根据三视图摆小正方体，结果只有一种吗

文︳王凯成

根据三视图摆小正方体，结果只有一种吗

文︳王凯成

解：根据从正面看及从左面看2

个不同方向看到的2个平面图形可

知，原来的立体图形只有一层。由从

上面看的图形“田”字知，一共有2×2=4（个）小正方体木块，摆成2行2列的方阵。只有一种摆法（如图3所示）。

例2一个由相同的小正方体木块组成的立体图形，无论正面看、左面看、上面看都是“田”字形状（如图4所示）。你能摆出这个立体图形吗？

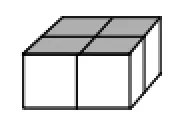
图3

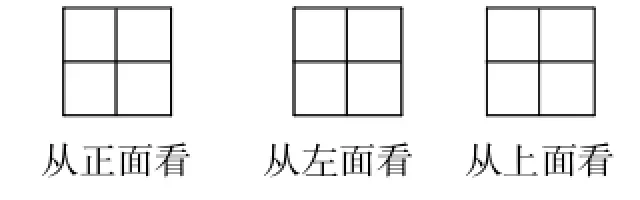
图4

解：根据从正面看及从左面看2个不同方向看到的2个平面图形可知，原来的立体图形是上下两层。由从上面看的图形“田”字知，下层有2× 2=4（个）小正方体木块，摆成2行2列方阵。上层至少有2个小正方体木块，最多有4个小正方体木块。

可以分三类情况摆放。

（1）在下层2行2列方阵的左对角线位置上面各摆1个小正方体木块构成上层。这时有4+2=6（个）小正方体木块（如图5所示）。

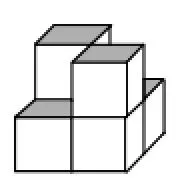
图5

（2）在下层2行2列方阵的左对角线位置上面各摆1个小正方体木块，再在右对角线的2个位置中的一个摆1个小正方体木块构成上层。这时有4+3=7（个）小正方体木块（如图6所示）。

图6

（3）上下2层，每层有4个小正方体木块，都摆成2行2列方阵。这时有4×2=8（个）小正方体木块（如图7所示）。

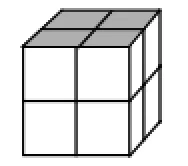
图7

例3由13个相同的小正方体木块构成一个立体图形，从3个不同方向看这个立体图形，得到3个平面图形（如图8所示），你能根据这3个平面图形摆出所观察到的立体图形吗？

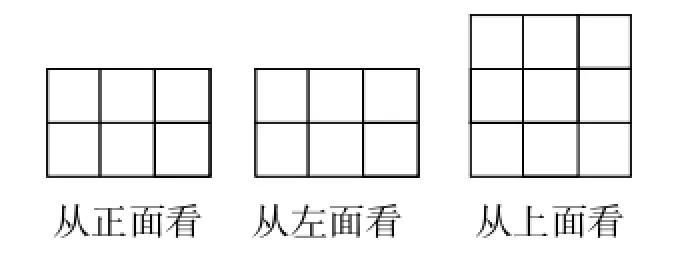
图8

解：根据从正面看及从左面看2个不同方向看到的2个平面图形可知，原来的立体图形是上下两层。由从上面看的图形“九宫格”知，下层有3×3=9（个）小正方体木块，摆成3行3列方阵。所以上层有13－9=4（个）小正方体木块。

可以分三类情况摆放。

（1）在下层3行3列方阵的左对角线位置上面各摆1个小正方体木块（如图9所示），剩下的4－3=1（个）小正方体木块可以在上层的9－3=6（个）位置上任意摆放。

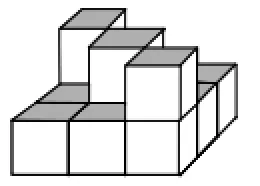
图9

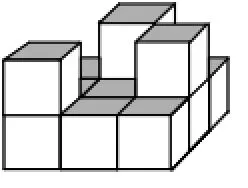
图10

（2）在下层3行3列方阵（从正面看）的第一行最左面位置、第二行最右面位置、第三行中间位置上面各摆1个小正方体木块（如图10所示），剩下的4－3=1（个）小正方体木块可以在上层的9－3=6（个）位置上任意摆放。

（3）在下层3行3列方阵的最左面一行和最前面一行，除交叉位置外，上面各摆1个小正方体木块构成上层，这时正好用完9+4=13（个）小正方体木块（如图11所示）。

图11

例4一个由相同的小正方体铁块焊接成的立体图形，无论从正面看、左面看、上面看都是“田”字形状（如图12所示）。你能想象出这个立体图形吗？

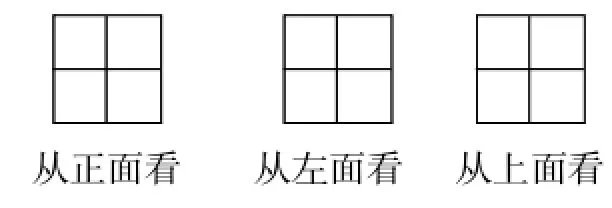
图12

解：根据从正面看及从左面看2个不同方向看到的2个平面图形可知，原来的立体图形是上下两层。由从上面看的图形“田”字知，原来的立体图形最少有2×2=4（个）小正方体铁块，最多有4×2=8（个）小正方体铁块。

（1）在下层2行2列方阵的左对角线位置上各摆1个小正方体铁块构成下层，下层有2个小正方体铁块。在上层2行2列方阵的右对角线位置上各摆1个小正方体铁块构成上层，上层也有2个小正方体铁块。这时用2+2=4（个）小正方体铁块焊接成立体图形。

（2）在（1）的基础上，可以增加1个或2个或3个或4个小正方体铁块焊接成立体图形。

从例1、例2、例3、例4的解析可见，不管小正方体的个数给定或不给定，根据3个不同方向看到的3个平面图形所确定的立体图形不一定只有一种，有时有一种，有时有多种，但一定是有限种。

观察物体（三）根据三视图想象构造立体图形，是培养学生空间想象能力的好素材。笔者建议把小结“根据三个方向观察到的形状摆小正方体，结果只有一种哦！”修改为“根据三个方向观察到的形状摆小正方体，能够锻炼你的想象能力哦！”

（作者单位：陕西省小学教师培训中心）

表内乘法口诀是人教版数学二年级下册的内容。为了帮助学生有效记忆表内乘法口诀，更快、更好地背诵表内乘法口诀，在教学过程中，教师应注重以下几个环节。

一、追本溯源，探寻规律

追寻乘法口诀的本源，理解记忆。在学习乘法口诀之前，学生先认识乘法，理解乘法的含义。在此基础上，理解乘法口诀的含义，可以帮助学生记忆乘法口诀。

从已有经验入手，方便记忆。根据教材安排，可利用学生熟悉的“5个5个地数”的经验，首先教5的乘法口诀。在理解的基础上，引导学生先记住5的乘法口诀的得数是5、10、15、20、25，再记忆5的乘法口诀，这样学生会记得快、记得牢。

引导发现规律，自主记忆。对于每组口诀，在引导记忆的阶段，都先让学生观察每组的得数，在发现每组相邻两句乘法口诀之间的关系后，还要引导学生寻找自己的发现。如对8的乘法口诀，孩子们发现：从8开始，分别是个位减2，十位加1，只有40加8得48除外。学生借助自己的发现记口诀，记得更快、更好。特别是9的乘法口诀，学生的方法就更多了。除了延伸8的乘法口诀的规律“个位逐个减1，十位逐个加1”外，学生还有如下发现：十位上的数加个位上的数的和都是9；几个9的得数就是几个10减几；几个9的得数的十位上的数比几少1，再根据十位上的数确定个位上的数是9减几。学生发现这些规律后，自由选择自己喜欢的方式记住9的乘法口诀就容易多了。

二、形式多样，整体背诵

脱离情境进行抽象记忆。对每组口诀，教材都安排了一定的情境帮助学生学习理解。在学习完表内乘法口诀后，可引导学生横着、竖着观察，找到每组相邻两句乘法口诀之间的联系：横排，每组相邻两句乘法口诀得数相差的数相同，即“几的口