一类常微分方程边值问题的格林函数的讨论

马 慧

(南京财经大学 应用数学学院，江苏 南京 210003)

一类常微分方程边值问题的格林函数的讨论

马 慧

(南京财经大学 应用数学学院，江苏 南京 210003)

为了研究方便，通常应用格林函数将微分方程转化为与其等价的积分方程。通过常数变易法研究了一类三阶常微分方程在一类边值条件下的格林函数求法，也给出了另一类边值条件下微分方程的格林函数表达式，最后给出了一些上述方程求解格林函数的实例。

格林函数； 边值问题； 三阶常微分方程

0 引言

Green函数[1]在求解常微分方程中是十分关键的，可以通过格林函数把微分方程转化为积分方程来求解平面动力问题等。在实际生活中，线性常微分方程的解通常可用Green函数的显式来表示；而相应的非线性常微分方程的边值问题[2]，则需要通过Green函数将其转化为积分方程来求解。

在求解Green函数时，通常要考虑2个方面，其一是常微分方程，其二是边值条件，因而求解方法不统一。葛渭高[3]研究了共振边值条件下的Green函数求法；孙经先[4]给出了Sturm-Liouville两点边值问题的Green函数表达式；Kafri等[5]则给出了推广的Sturm-Liouville两点边值问题的Green函数表达式；Zhao[6]研究了二阶常微分方程三点边值问题的Green函数；Nieto等[7]考虑了二阶周期边值问题的Green函数；Seifert[8]考察了二阶中立时滞边值问题的Green函数。上述都是传统经典的方法，但是遇到特殊微分方程及边值问题时，计算尤为复杂，因此本文给出了一类特殊三阶微分方程的Green函数求法，具体方程如下：

L(y)≡y'''(x)-k2y'(x)=0,x∈[α,β],k≠0

(1)

求解出该方程在一种边值条件下的Green函数(其中L为算子)，由此推广到其他边值条件下的Green函数。

本文首先给出Green函数的定义及其构造方法[9]，其次研究了一类三阶常微分方程(1)在多种边值条件下的Green函数，最后给出了求解三阶常微分方程(1)在不同边值条件下的Green函数的实例。

1 Green函数的定义及其构造

给定三阶常微分方程(1)及边值条件：

(2)

其中y(j)(α),y(j)(β)(j=1,2)的一次式Vk(k=1,2,3)是线性独立的。

定义[10]设ε为(α，β)中任意一点，则具有以下4条性质的函数G(x,ε)称为边值问题(1)、(2)的Green函数。

1)在[α，β]区间内，函数G(x,ε)，G'x(x,ε)在点x=ε处连续；

2)G(x,ε)关于x的二阶导数，以x=ε为第1类间断点，且其跃度为-1，即:

(3)

3)作为x的函数,G(x,ε)在[α，ε),(ε,β]是方程(1)的解L(G)=0；

4)作为x的函数，满足边值条件(2)Vk(G)=0(k=1,2,3)。

Green函数构造：

设y1(x),y2(x),y3(x)是方程(1)的线性无关解，由性质(3)知函数G(x,ε)在[α，ε),(ε,β]上可由上述y1(x),y2(x),y3(x)表出，即:

(4)

其中a1,a2,a3,b1,b2,b3都为ε的待定函数。

由性质(1)、(2)知函数G(x,ε)，G'x(x,ε)在点x=ε处连续，且G''x(x,ε)在点x=ε处的跃度为-1，即:

[b1y1(ε)+b2y2(ε)+b3y3(ε)]-[a1y1(ε)+a2y2(ε)+a3y3(ε)]=0,

[b1y'1(ε)+b2y'2(ε)+b3y'3(ε)]-[a1y'1(ε)+a2y'2(ε)+a3y'3(ε)]=0,

[b1y''1(ε)+b2y''2(ε)+b3y''3(ε)]-

[a1y''1(ε)+a2y''2(ε)+a3y''3(ε)]=-1。

设ck=bk-ak,k=1,2,3

(5)

于是得到关于ck(ε)的线性方程组：

(6)

方程组(6)的系数行列式为Wronski行列式W(y1(x),y2(x),y3(x))在点x=ε时的值，因为y1(x),y2(x),y3(x)线性无关，所以W(y1(ε)，y2(ε),y3(ε))≠0,故方程组(6)有唯一解ck(ε)(k=1,2,3)。

下面求ak(ε),bk(ε)(k=1,2,3)。

对于边值条件(2)中的Vk(y),设Vk(y)=Ak(y)+Bk(y),其中：

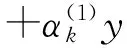
由式(4)得：

同理有：

Bk(G)=b1Bk(y1)+b2Bk(y2)+b3Bk(y3)。

再根据性质(4)可知Vk(y)=Ak(y)+

Bk(y)=0(k=1,2,3),即：a1Ak(y1)+a2Ak(y2)+a3Ak(y3)+b1Bk(y1)+b2Bk(y2)+b3Bk(y3)=0(k=1,2,3)。

又由式(5)知bk=ak+ck，则：

a1Ak(y1)+a2Ak(y2)+a3Ak(y3)+(a1+c1)Bk(y1)+(a2+c2)Bk(y2)+(a3+c3)Bk(y3)=0

(k=1,2,3)。

于是：

a1Vk(y1)+a2Vk(y2)+a3Vk(y3)=c1Vk(y1)+c2Vk(y2)+c3Vk(y3),k=1,2,3

(7)

方程组(7)为关于a1,a2,a3的线性方程，由Vk(k=1,2,3)线性无关知方程组的系数行列式为：

因此方程(7)的解a1,a2,a3存在且唯一。由bk=ak+ck知bk(ε)(k=1,2,3)也存在且唯一。将ak(ε),bk(ε)(k=1,2,3)代入式(4)就得到了G(x,ε)，因此可得到下面的引理。

引理1 如果边值问题(1)、(2)只有零解y(x)=0，则算子L有且只有一个Green函数。

2 一类边值问题下的Green函数证明

首先设方程(1)边值条件为：

y(α)=2y(β),y'(α)=y'(β),y''(α)=

y''(β)

(8)

有以下结论。

定理1 三阶边值问题(1)、(8)的Green函数为：

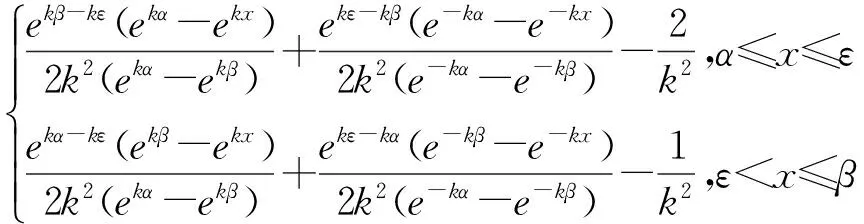
(9)

证明 已知方程组(1)的基本解组为1，ekx,e-kx,则通解为y=A+Bekx+Ce-kx，其中A,B,C为任意常数。由边界条件(8)，可得到A,B,C满足下列等式：

从而得到A=B=C=0，故由引理1知Green函数存在且唯一。

因此可以根据基本解组1，ekx,e-kx,以及性质(3)设Green函数的形式如下：

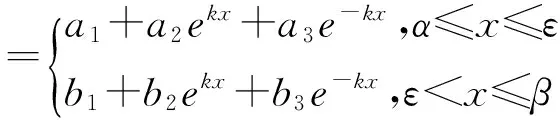
(10)

其中ak(ε),bk(ε)(k=1,2,3)都为ε的待定函数。

设ck=bk-ak(k=1,2,3),由方程(6)可得到关于ck(ε)的线性方程组：

解得：

(11)

由性质(4)可知Green函数应满足边值条件(4)，则对边值问题(3)、(4)应有：

G(α,ε)=2G(β,ε),G'x(α,ε)=G'x(β,ε),G''x(α,ε)=G''x(β,ε),即：

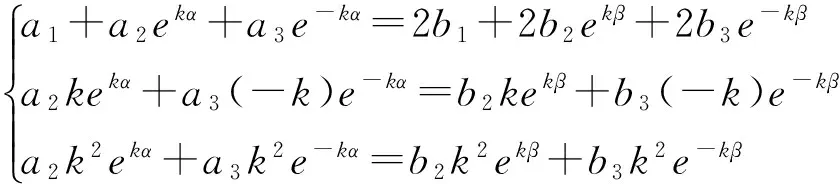
(12)

再由式(5)、(11)、(12)可得：

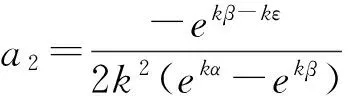
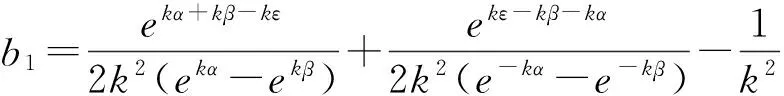
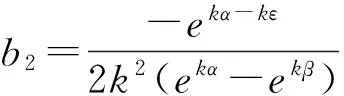
把所求的系数a1,a2,a3,b1,b2,b3代入式(5)即可到问题(3)、(4)的Green函数为：

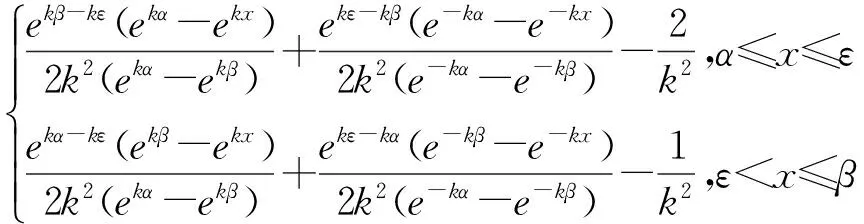
(13)

3 另一类边值问题下的Green函数

关于下面这一类边值条件下Green函数的证明过程与上述边值条件下Green函数的证明类似，因此直接给出所述问题的Green函数。定理2提出的思路可参考文献[11]。

k≠0,其Green函数为：

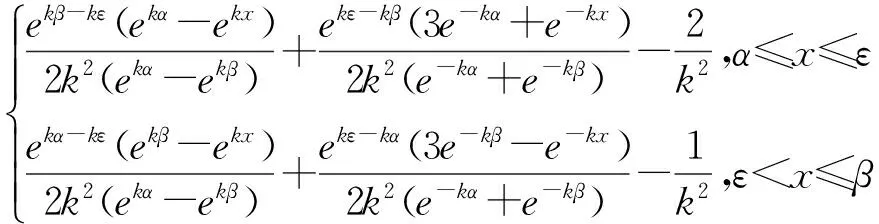
(14)

4 计算Green函数的实例

在实际求解Green函数时，可以使用定义，关于定义的求法与本文研究的三阶常微分方程类似，故不再举例说明；也可以直接使用公式，下面举例说明。

例1 求解三阶常微分方程y'''(x)-

y'(x)=0,x∈[0,1]，在边值条件y(0)=2y(1),y(0)'=y'(1),y''(0)=y''(1)下的Green函数。

解 本例中k=1,α=0,β=1，由式(13)可得Green函数为：

G(x,ε)=

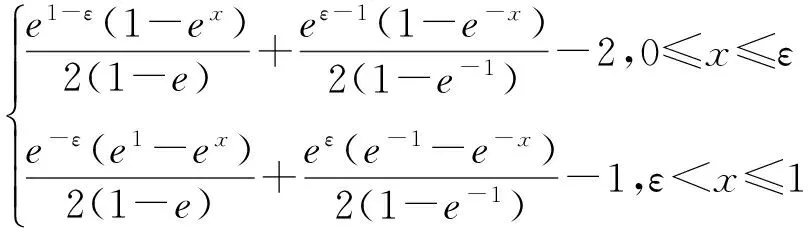
例2 求解三阶常微分方程y'''(x)-4y'(x)=0,x∈[0,1]，在边值条件y(0)=2y(1),2y'(0)=y''(1),y''(0)=2y'(1)下的Green函数。

解 本例中k=2,α=0,β=1，由式(14)可得Green函数为：

G(x,ε)=

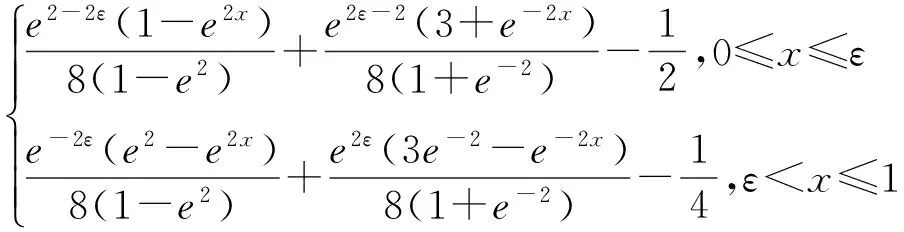
[1] Hartman P.Ordinary Differential Equations[M].New York:Addison Wiley,1964:251.

[2] 郭大钧,孙纪先，刘兆理.非线性常微分方程泛函方法[M].2版.济南：山东科学技术出版社,2005:35-44.

[3] 葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007:23-26.

[4] 孙经先.非线性泛函分析及其应用[M].北京:科学出版社,2008:17-20.

[5] Kafri HQ,Khuri SA.Bratu's problem:A novel approach using fixed-point iterations and Green's functions[J].Computer Physics Communications,2016,198:97-104.

[6] Zhao Z.Solutions and Green's functions for some linear second-order three-point boundary value problems[J].Computers and Mathematics with Applications,2008,56:104-113.

[7] Nieto JJ,Rodríguez-López R.Green's function for second-order periodic boundary value problems with piecewise constant arguments[J].Journal of Mathematical Analysis & Applications,2005,304(1):33-57.

[8] Seifert G.Second-order neutral delay-differential equations with piecewise constant time dependence[J].Journal of Mathematical Analysis & Applications,2003,281(1):1-9.

[9] 李莉.一类二阶常微分方程边值问题的格林函数的讨论[J].菏泽学院学报, 2013,35(2): 5-9.

[10] 沈以淡.积分方程[M].北京:清华大学出版社,2012:213.

[11] 赵增勤.一类常微分方程边值问题的格林函数求法[J].商丘师范学院学报,2009,25(3):1-6.

(责任编辑 吴鸿霞)

Discussion on Green Function for a Class of Boundary Value Problems of Ordinary Differential Equations

MaHui

(School of Applied Mathematics,Nanjing University of Finance & Economics,Nanjing Jiangsu 210003)

In order to study conveniently,the differential equation is transformed into its equivalent integral equation by using Green's function.The Green function for a third-order ordinary differential equation with a boundary condition was studied by the method of variation of constant.The expression of the Green function for other boundary condition was also given.Finally some examples of Green function were provided for boundary value problems of ordinary differential equations.

Green function;boundary value problem;third-order ordinary differential equation

2016-12-28

马慧，硕士生。

10.3969/j.issn.2095-4565.2017.02.011

O29

A

2095-4565(2017)02-0050-04