节点域尺寸对钢框架节点塑性损伤分布规律的影响

张 毅，包恩和

(桂林理工大学 广西岩土力学与工程重点实验室，广西 桂林 541004)

节点域尺寸对钢框架节点塑性损伤分布规律的影响

张 毅，包恩和

(桂林理工大学 广西岩土力学与工程重点实验室，广西 桂林 541004)

为了研究节点域尺寸对钢框架节点塑性损伤分布规律的影响，以钢框架结构中常见的“十字型”梁柱节点为研究对象，通过节点域受力的平衡准则，着重对柱类型(箱型、钢管)、柱轴压比、梁柱截面高度比、柱宽度与层高比及结构跨高比等基本参量进行了分析。分析结果表明：梁、柱及其节点域组成的钢框架节点的塑性铰位置按不考虑节点域尺寸来判断时可能会出现误差。随柱轴压比、梁柱截面高度比增加，节点域与柱的强度比增加；而随跨高比的增加，节点域与柱的强度比减小。箱型柱钢框架结构的柱轴压比小于等于0.4时，柱强度为节点域强度的1.0倍至2.5倍。实际工程柱梁尺寸范围内，钢管柱钢框架的节点域强度大于同截面的柱强度。

柱类型；柱轴压比；节点域；梁柱截面高度比

0 引言

根据中国现行抗震规范进行钢框架结构设计时，一般情况下，在钢框架结构的强度、变形计算中，不考虑节点域强度及剪切变形等的影响。为了明确钢框架结构中节点域的受力性能及其影响因素，合理完善钢框架结构的设计方法，国内外的学者进行了相关研究。文献[1]针对钢结构连接提出了一种改进的分析模型,在钢结构设计的三维分析过程中，考虑了节点的非线性响应，并据此建立了不同类型节点的标准化分析模型。文献[2-3]对箱型柱与梁异型节点进行了滞回性能试验，试验结果表明：节点域剪力-剪切变形滞回曲线稳定，节点域的抗震性能良好。并根据试验结果与理论分析，建立了箱型柱与梁异型节点的节点域抗剪承载力计算公式。文献[4]对钢管柱-H型梁节点进行了抗震性能试验，得到了节点域剪切变形耗能强的结论。文献[5]对不同规格H型钢构成的边钢框架梁、柱T型节点进行了低周反复试验，并对节点域的延性和耗能特性进行了评价。文献[6-7]构建了考虑节点域的平面钢框架柱、梁单元刚度矩阵，通过弹性方法对平面钢框架结构的内力及变形进行了分析和计算，发现考虑节点域后钢框架侧向刚度变小，同时钢框架变形量增大。文献[8-10]基于非线性分析平台，对不考虑节点域尺寸的多层钢结构静力损伤和动力损伤分布机理进行了研究。

上述研究成果有效地推动了钢结构工程在各领域的应用与发展。由于构件形式及其节点构造方式的多样化，还需进一步研究钢结构节点的受力性能，特别是有关节点域尺寸对箱型柱及钢管柱钢框架损伤分布规律影响的理论研究偏少。为此，本文以常见的梁、柱及节点域组成的十字型钢框架结构为分析对象，以柱类型(箱型、钢管)、柱轴压比、梁柱截面高度比、柱宽度与层高比及结构跨高比等为主要研究参量，基于节点域周围力平衡准则进行分析，分析了节点域尺寸对箱型柱及钢管柱钢框架节点损伤分布规律的影响。

1 研究模型

分析模型为整体形状规则的钢框架，局部钢框架内部由柱、梁和节点域组成，如图1a所示。局部钢框架柱截面上下层相同、梁截面左右跨相同，如图1b所示。分析模型的柱、梁及节点域均为刚接，支座均为铰接，外荷载为水平荷载V和柱轴压力N，如图1c所示。柱截面形式有箱型及钢管，梁均为H型钢。图1中：hc和hb分别为柱和梁的截面高度，mm；H为层高，m；L为跨度，m；层高H与跨度L相等；V为水平荷载，kN；N为柱轴压力，kN。

(a) 局部钢框架选取(b) 局部钢框架样式(c) 局部钢框架计算简图

图1 局部钢框架分析模型及计算简图

2 模型分析

2.1 模型受力分析

在水平荷载V和柱轴压力N作用下，分析模型的柱端受力、梁端受力和节点域的受力分布，如图2a所示。柱、梁端及交点O(柱、梁轴线交点)处的弯矩分布如图2b所示。

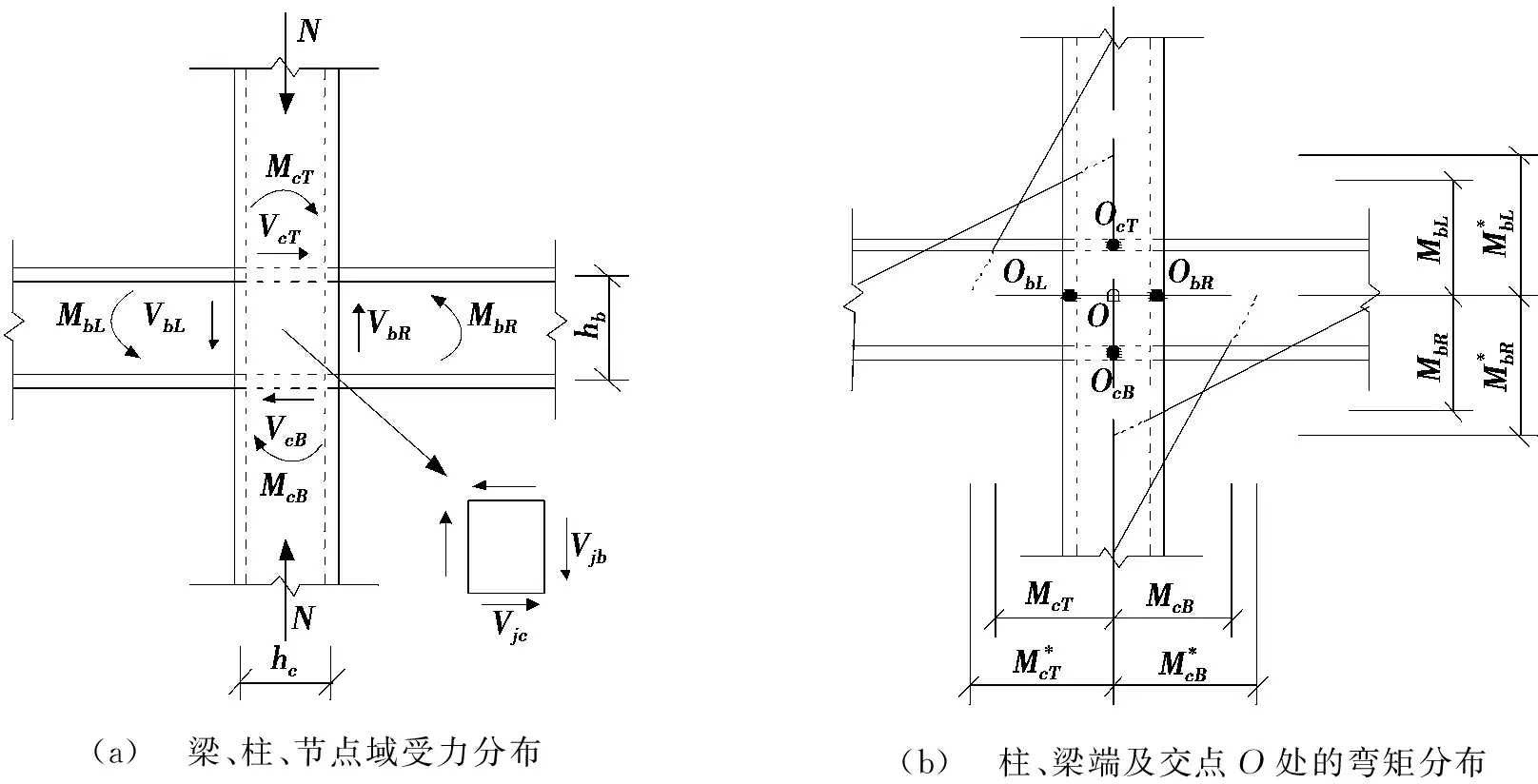
(a) 梁、柱、节点域受力分布(b) 柱、梁端及交点O处的弯矩分布

图2 模型受力分析示意图

如图2a所示，分析模型梁、柱截面高度为hb、hc，节点域截面和柱截面相同。基于节点域周围力平衡准则，节点域弯矩Mj的计算公式为：

Mj=Vjbhc=Vjchb；

(1)

(2)

(3)

其中： VcT=VcB=V；VbL=VbR=V(H-hb)/(L-hc)；MbL=MbR=0.5V(L-hc)；McT=McB=0.5V(H-hb)。

由节点域柱梁轴线交点O处建立的弯矩公式为：

(4)

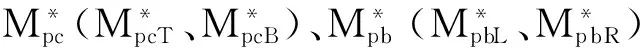
(5)

(6)

(7)

2.2 柱、梁及节点域的交点O处强度比

分析模型的柱、梁及节点域在柱梁轴线交点O处强度比，定义公式如下。

强柱系数：

(8)

节点域与柱强度比：

(9)

节点域与梁强度比：

(10)

2.3 节点域尺寸对结构塑性铰形成位置的影响

在分析模型的柱、梁轴线交点O处，将柱、梁及节点域的全截面塑性弯矩(式(5))代入式(6)中，VbL、VbR、VcT、VcB计算公式如下：

VbL=VbR=2Mpb/(L-hc)；

(11)

VcT=VcB=2Mpc/(L-hb)。

(12)

式(7)中，剪力是对应节点域的交点O处弯矩为全截面塑性弯矩时的剪力，因此，柱、梁剪力计算公式为：

(13)

(14)

将式(11)～式(14)代入式(5)～式(7)中，整理后得如下公式：

(15)

(16)

(17)

整理式(8)～式(10)和式(15)～式(17)，可得如下公式：

(18)

(19)

(20)

其中：Rpcb、Rpjc及Rpjb分别为不考虑节点域尺寸时，分析模型强柱系数、节点域与柱强度比及节点域与梁强度比，Rpcb=Mpc/Mpb，Rpjc=Mpj/2Mpc，Rpjb=Mpj/2Mpb。

以柱宽与跨度比(hc/L)、梁高与层高比(hb/H)为参数，考虑节点域尺寸和不考虑节点域尺寸的强度比，结果见图3。

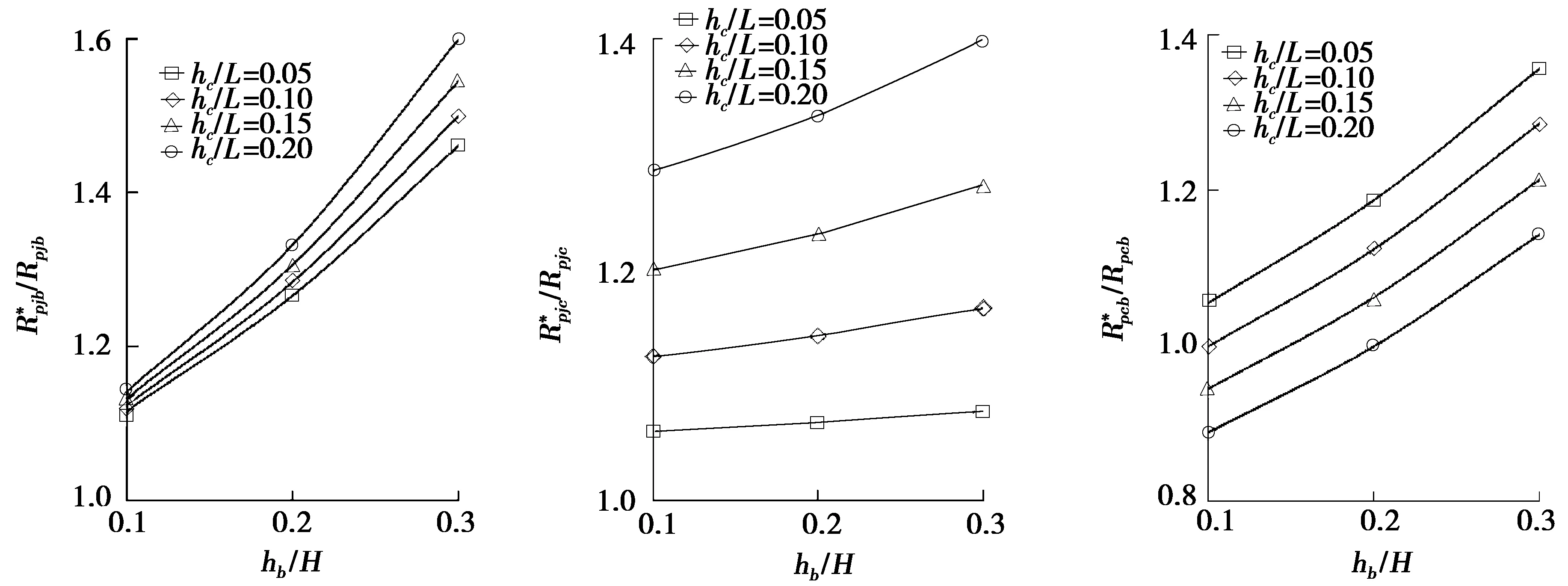
与hb/H的关系与hb/H的关系与hb/H的关系

基于以上分析，不考虑节点域尺寸的模型构件强度比和考虑节点域尺寸的模型构件强度比不一致。一般情况下，柱、梁及节点域组成的局部钢框架连接处破坏机制，按不考虑节点域尺寸来判断塑性铰的位置时，可能会出现误差。

2.4 节点域与柱强度比对结构塑性损伤机理的影响

根据文献[11-12]，柱截面形式为箱型和钢管的情况下，节点域全截面塑性弯矩Mpj的计算公式为：

(21)

考虑柱轴压比μ的箱型截面的塑性截面抵抗矩Wpc的计算公式为：

(22)

考虑柱轴压比μ的钢管截面的塑性截面抵抗矩Wpc的计算公式为：

(23)

其中：d为钢管的直径。

整理式(19)和式(21)～ 式(23)，可得节点域和柱强度比公式。

箱型截面：

(24)

钢管截面：

(25)

图4和图5分别为箱型柱、钢管柱十字型局部钢框架模型的节点域与柱强度比-轴压比关系，其中，节点域宽度与层高比(hc/H)分别为0.1、0.2。

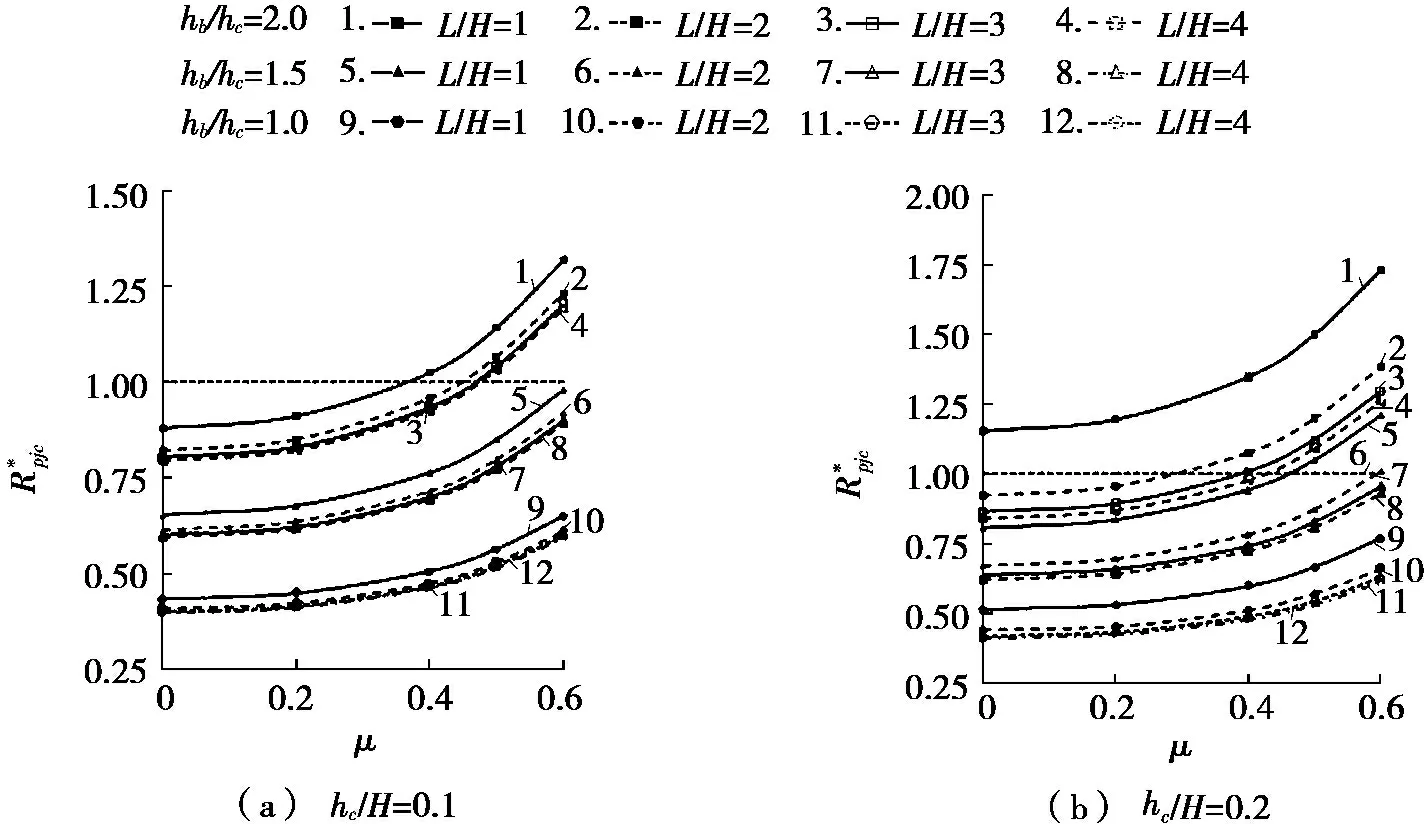
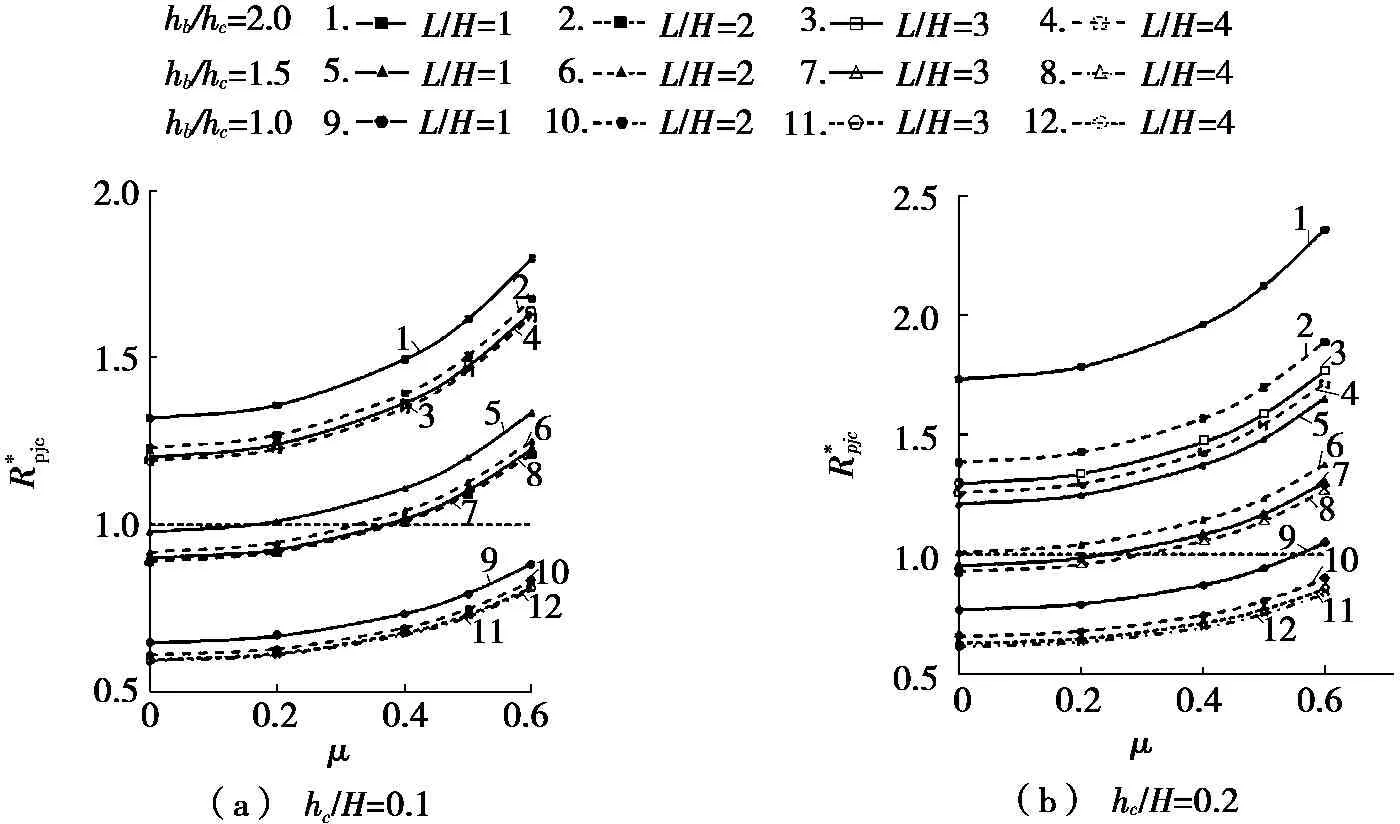
图4 节点域与柱的强度比-轴压比关系(箱型柱)

图5 节点域与柱的强度比-轴压比关系(钢管柱十字型)

由图4和图5可知：随着轴压比、梁柱截面高度比的增加，节点域与柱的强度比增加；而随着跨高比的增加，节点域与柱的强度比减小。柱宽与层高比值由0.1增加到0.2时，节点域与柱的强度比有增大的趋势。

箱型柱模型的柱宽与层高比为0.1时的节点域与柱强度比随轴压比的变化如图4a所示。由图4a可知：当梁柱截面高度比为2.0且轴压比大于0.4时，节点域与柱的强度比都大于1，最大值为1.40，柱先于节点域屈服；其他状况时，节点域先于柱屈服。箱型柱模型的柱宽与层高比为0.2时的情况如图4b所示，当梁柱截面高度比为2.0、跨高比为1，或梁柱截面高度比为2.0、跨高比为2至4、轴压比大于等于0.4，或梁柱截面高度比为1.5、跨高比为1、轴压比大于等于0.4时，节点域与柱的强度比均大于1，柱先于节点域屈服；其他状况时，节点域先于柱屈服。由此可知，箱型柱模型的轴压比小于等于0.4时，节点域先于柱屈服，节点域与柱的强度比为0.4～1.0，柱强度为节点域强度的1.0～2.5倍。

钢管柱模型的柱宽与层高比为0.1时的节点域与柱强度比随轴压比的变化如图5a所示，当梁柱截面高度比分别为1.5和2.0，且轴压比大于等于0.4时，节点域与柱的强度比均大于1，最大值为1.8，柱先于节点域屈服；其他状况时，节点域先于柱屈服。钢管柱模型的柱宽与层高比为0.2时的情况如图5b所示，梁柱截面高度比为1.0时，节点域与柱的强度比小于1，节点域先于柱屈服；其他状况时，柱先于节点域屈服。由此可知，在实际工程梁柱尺寸范围内，钢管柱钢框架的节点域强度大于柱强度。

3 结论

(1)柱、梁及节点域组成的钢框架节点的塑性铰位置，按不考虑节点域尺寸来判断时可能会出现误差。

(2)随轴压比、梁柱截面高度比增加，节点域与柱强度比增加；而随跨高比增加，节点域与柱强度比减小。

(3)箱型柱分析模型的轴压比小于等于0.4时，基本上节点域领先柱屈服，节点域与柱强度比值为0.4～1.0，柱强度为节点域强度的1.0～2.5倍。

(4)钢管柱分析模型，梁柱截面高度比为1.0时，节点域与柱强度比值小于1，节点域先于柱屈服，其他情况下，柱先于节点域屈服。

[1]HSIEHSH,DEIERLEINGG.Nonlinearanalysisofthree-dimensionalsteelframeswithsemi-rigidconnections[J].Computersandstructures,1991,41(5):995-1009.

[2] 薛建阳,刘祖强,彭修宁,等.大型火电主厂房钢结构异型节点抗震性能试验研究[J].建筑结构学报,2011,32(7):133-140.

[3] 薛建阳,胡宗波,彭修宁,等.钢结构箱形柱与梁异型节点抗剪承载力分析[J].土木工程学报,2011(8):9-15.

[4] 王伟,王明兴,陈以一,等.钢管柱-H形梁内加劲铸钢模块节点抗震性能试验研究[J].建筑结构学报,2015,36(3):71-79.

[5] 李许峰,王新武.边钢框架节点抗震性能试验[J].河南科技大学学报(自然科学版),2016,36(6):55-60.

[6] 贾连光,白宏涛,史永斌,等.建立考虑节点域剪切变形的平面钢框架单元刚度矩阵[J].沈阳建筑大学学报(自然科学版),2007,23(1):11-15.

[7] 韩明岚,王燕,董建莉.梁翼缘削弱式钢框架考虑节点域剪切变形的力学性能研究[J].建筑钢结构进展,2013,15(1):22-28.

[8] 陈宜虎,赵艳林,包恩和,等.多层屈曲约束斜撑钢框架抗震性能研究[J].同济大学学报(自然科学版),2016,44(4):512-519.

[9] 包恩和,陈宜虎.多层屈曲约束支撑钢框架抗震性能研究[J].结构工程师,2013,29(6):98-105.

[10] 包恩和,黄美玲,曹邕生,等.多层规则钢框架连体结构动力响应机理研究[J].科学技术与工程,2015,15(33):79-84.

[11] 日本建築学会.鋼構造接合部設計指針[M].东京:日本建築学会,2006:206-207.

[12] 井上一朗.建築鋼構造の理論と設計[M].京都:京都大学学術出版会,2003:14-16.

国家自然科学基金项目(51409051，51368014);广西岩土力学与工程重点实验室基金项目(2015-B-04)

张毅(1978-),男,河北邯郸人,讲师,博士生,主要从事钢结构理论及应用等方面的研究;包恩和(1975-),男,通信作者,内蒙古乌兰察布人,副教授,博士，硕士生导师，主要从事钢结构理论及应用等方面的研究.

2016-11-15

1672-6871(2017)04-0060-06

10.15926/j.cnki.issn1672-6871.2017.04.013

TU392

A