一种面向检索的三维模型多特征最优融合方法
李 亮,白晓亮,卫青延
(1.中国空空导弹研究院,洛阳 471009;2.西北工业大学 现代设计与集成制造技术教育部重点实验室,西安 710072)
一种面向检索的三维模型多特征最优融合方法
李 亮1,白晓亮2,卫青延1
(1.中国空空导弹研究院,洛阳 471009;2.西北工业大学 现代设计与集成制造技术教育部重点实验室,西安 710072)
针对不同检索场景下三维模型的多特征融合问题,提出一种三维模型的多特征最优融合方法,该方法利用粒子群算法,采用监督学习模式在不同场景下依次完成最合适特征的挑选并计算最合理的权重,进而确定出针对指定检索场景的最优特征融合方案。实验结果显示,该方法能够充分迎合不同检索场景的特点,与现有同类方法相比,能更有效地发挥多特征融合在用于三维模型检索时的优势和效果。
三维模型检索;多特征融合;粒子群算法
0 引言
随着三维模型已成为产品研制过程越来越不可获取的基础信息载体,为了应对愈加复杂和不确定的市场需求环境,如何有效地检索并重用企业已有的三维模型资源,进而缩短新产品的研制周期,已成为研究热点之一[1,2]。在目前对三维模型检索技术的研究中,如何描述模型对象进而准确衡量不同模型的相似性是其中的核心问题[3]。迄今为止,虽然已有众多的三维模型特征提取方法被学者们提出,例如著名的光场算法[4]、球面调和算法[5]等,然而不同方法由于受观察和处理三维模型的角度等因素制约,所提取的模型特征实质上都只是对三维模型某一特定方面的内容描述,以致尚未有一种方法能够完全适用所有模型对象。将多种模型特征按一定规则融合被认为是一种能够有效解决上述问题的处理方式,其目的在于对这些特征优势互补,从而更加完备地描述三维模型的内容信息以提升检索精度[3]。
由于三维模型检索技术的实际应用场景存在多样化的特点,例如根据企业需求的不同,用户所面对的检索对象往往分布于不同的模型数据库(例如回转体类模型库、棱柱类模型库,或是由多类模型所组成的混合类模型库等),因此,在进行多特征融合时,必须充分考虑不同检索场景下目标模型的特点。针对不同场景,是否选取到最合适的模型特征,以及是否对这些特征在检索目标模型时所起作用进行了最合理的权重分配,是保障多特征的融合效果,进而充分提升检索效果的重要影响因素。然而,现有三维模型多特征融合方法的设计主要是通过经验、或者某些简单的指标来对候选特征搭配取舍,如均值法[6]、单值评价指标法[7]等。这些工作虽然能够改善仅使用单一模型特征检索时的效果局限,但由于所给出的多特征融合方案并不能保证最优,限制了检索效果的提升空间。基于此,本文利用粒子群算法设计了一种三维模型的多特征最优融合方法,通过监督学习及启发式求解的策略确定出最优的特征融合方案,以期充分迎合不同检索场景的特点并提升最终的检索效果。
1 方法实现
本文方法的整体思路如图1所示,首先在训练阶段,针对不同检索场景下的三维模型训练集,根据候选特征的种类选择相应的特征提取方法对集合中的模型进行处理,并计算这些模型关于这些候选特征的相似度矩阵;在此基础上,利用粒子群算法寻找最适合进行融合的候选特征类别(即最优特征组合),并计算这些特征的对应权重(即最优特征权重),从而组成最优的特征融合方案;在测试阶段,根据上述融合方案对测试模型进行多特征的融合,进而据此获得不同模型之间的相似性评价。
1.1 预处理操作
为了获取三维模型多特征的最优融合方案,首先需要根据不同种类的特征分别计算不同模型间的相似度。由于不同特征的方法来源差异,导致模型相似度的计算结果在取值范围上也大相径庭,为了保证最终的融合效果,还需对其进行归一化处理。对于给定的由n个三维模型组成的模型训练集T={Mi},i=1,2,…,n,设k=1,2,…,K为候选特征的类别标签,为对T中的模型采用特征k所获得的模型相似度矩阵;其中,表示两个三维模型Mi和Mj之间的相似度(在本文实验中以模型间的特征距离度量)。在此之后,采用最小-最大规范化方法[8],将T中成员逐一处理以统一归化至[0,1]区间。
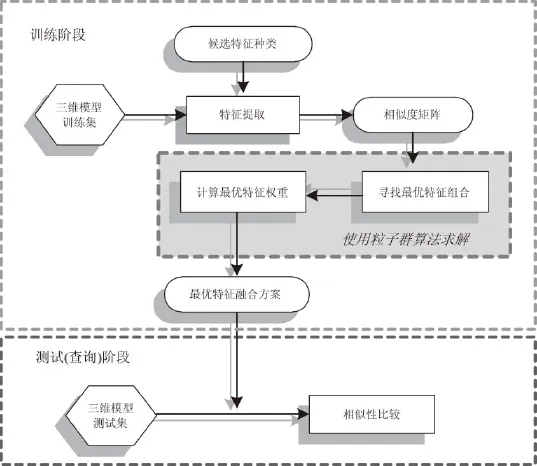
图1 方法整体思路
1.2 粒子群算法原理
粒子群算法源自对鸟群觅食行为的研究,是一种基于种群的模拟进化算法。与遗传算法、蚁群算法等其他进化算法相比,粒子群算法具有实施简单、调制参数较少等优点[9]。设集合为D维求解空间中一个由n个粒子(即可行解)所组成的种群,粒子群算法通过跟踪P中各粒子的位置和变化速度,以适应度值来评估当前粒子信息的优劣,并据此更新粒子自身的各体极值点PBesti以及整个种群的群体极值点GBest,进而指导各粒子不断调整自身速度和位置,逐步向着解空间中拥有全局最优适应度值的位置,即问题对象的最优解靠近。根据待处理对象的不同,粒子群算法又可进一步分为连续粒子群算法和离散粒子群算法。其中,前者主要针对解空间呈连续性的优化问题,通常按照如下规则[10]对粒子的速度和位置进行更新:
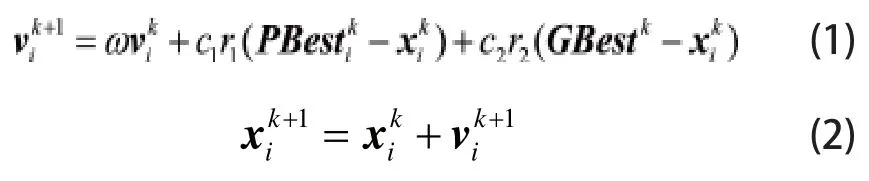
式中,k为算法当前的迭代次数;c1和c2为学习因子,分别用来控制粒子自身和整个种群对粒子运动的影响,通常取c1=c2=2;r1和r2为分布于[0,1]区间的随机数;ω为惯性权重,用来调节粒子速度的变化趋势。后者则用于求解0-1变量的离散优化问题,相应粒子速度和位置的更新规则可根据文献[11]设定为:
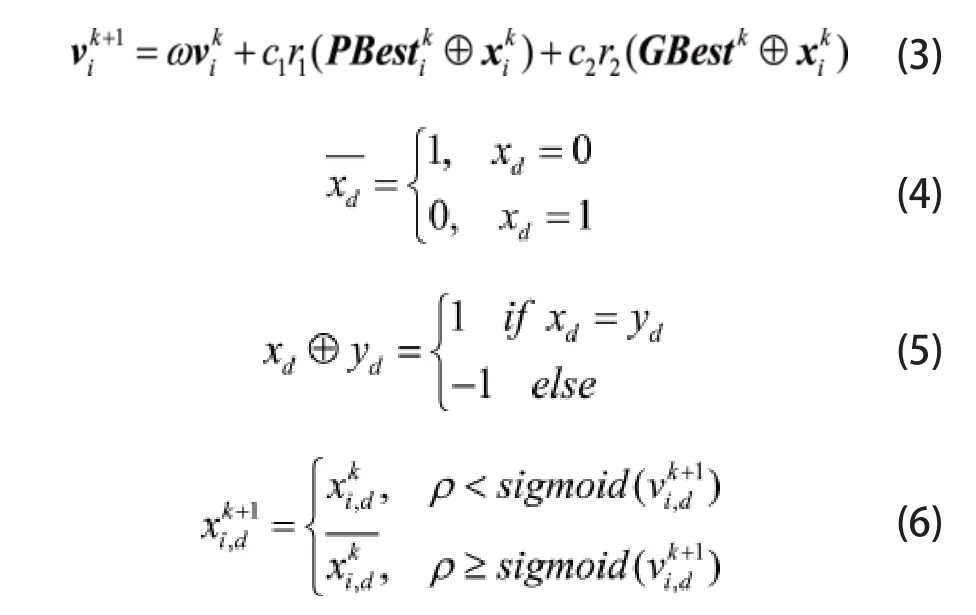
式中,xi,d和vi,d分别为粒子位置xi及速度vi在维度d上的分量;表示对xd的取反操作表示对同维度的两个粒子位置分量的比较操作;ρ为一个分布于0-1区间的随机数。
1.3 最优特征组合的寻找
对于如何从若干不同类别候选特征中选出最合适对象进行组合的问题,通过引入0-1变量ck(k=1,2,…,K)为候选特征的类别标签),并令:
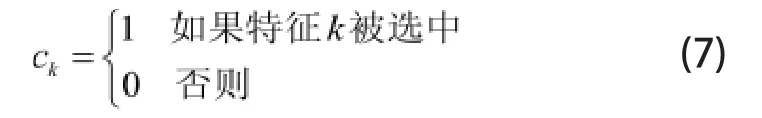
可将该问题的数学模型表示为:
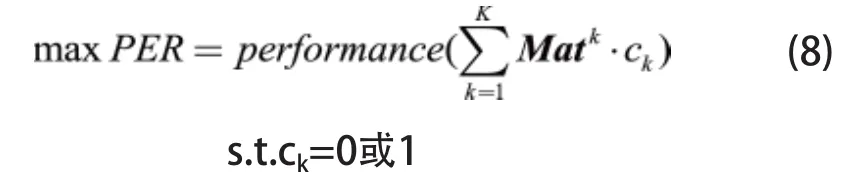
1)粒子编码方案
编码的目的是为了将粒子群算法中的粒子种群与实际问题建立联系。针对本小节的待解问题,假设存在K种三维模型候选特征,将每一套潜在的特征组合方案表示为一个粒子,则每个粒子Pi的编码为,其中xi,k的取值为0或1,用来描述各候选特征的入选情况。例如,当K=5,表示候选特征集合中的第1种和第5种候选特征入选参与组合。
2)适应度函数
本文以平均查准率[12]作为粒子适应度值的评价指标,以考察粒子对应的特征组合方案在检索中的使用效果,即:
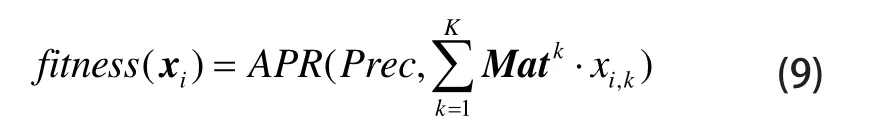
式中,APP(.)为平均查准率计算函数;Prec为训练集T中的模型预分类信息。
3)算法流程描述
寻找三维模型最优特征组合的算法流程如算法1所示,其中,以算法执行至最大迭代次数作为算法的终止条件。
算法1:三维模型最优特征组合的寻找
输入:候选特征的类别标签集合{k};模型训练集的相似度矩阵集合{Matk},集合成员与候选特征类别相对应。
输出:最优特征的类别标签集合{s}。
1)Begin;
2)初始化粒子群;
3)Do;
4)按照式(1)和式(2)分别计算粒子的位置和速度;
5)按照式(9)计算适应度,更新粒子个体极值和群体极值;
6)While未达到最大迭代次数;
7)Return{s};
8)End。
1.4 最优特征权重的计算
在获取三维模型的最优特征组合之后,对于如何为这一组合中的成员配置最优权重的问题,可将该问题的数学模型表示为:
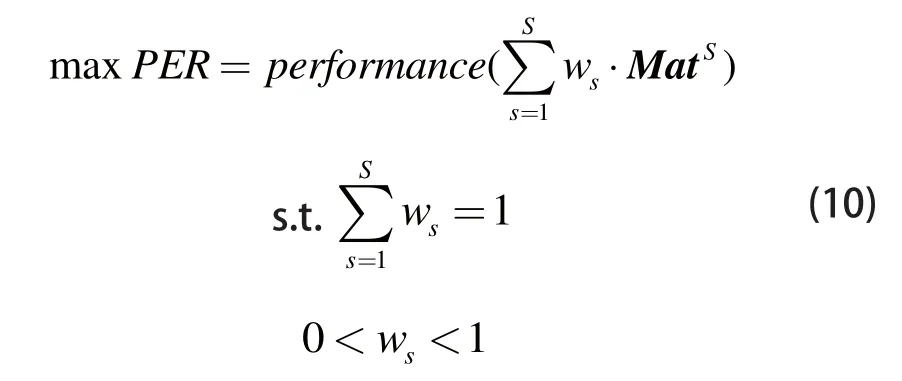
式中,performance(.)为检索结果的评价函数;s=1,2,…,S为最优特征的类别标签;ws为特征s的权重;为与特征s对应的模型训练集T的相似度矩阵。由上式可以看出,上述问题的实质是一个连续变量的约束极值问题,属于连续优化问题的范畴,因此采用连续粒子群算法进行求解。
1)粒子编码方案
针对此前获取的S种最优特征,将每一套潜在的权重配置方案表示为一个粒子,则每个粒子pi的编码为一个S维向量其中,向量成员xi,s的取值区间设为[0,1]。
2)适应度函数
结合本小节待求解问题的目标函数与约束条件,一般来讲,适应度函数可按如下方案设计:
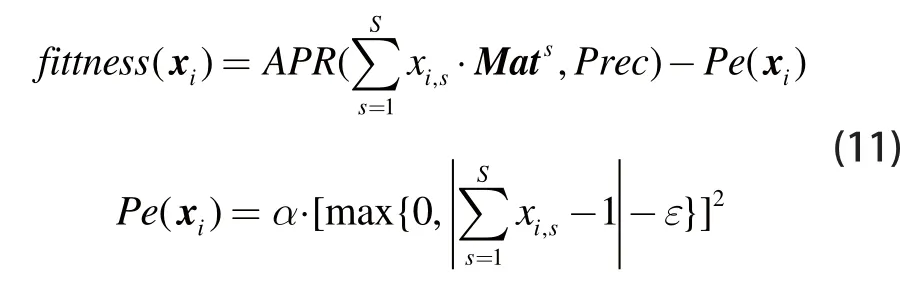
式中,APR(.)与Prec的定义与前一小节相同,此处不再赘述;Pe(.)为惩罚函数,用以限制粒子的取值以满足约束条件分别为惩罚因子和误差项。但是,该设计的主要缺点在于合适的惩罚因子和误差项通常很难找到,而不恰当的取值反而会阻碍粒子对可行解的搜索。
考虑到如果不使用惩罚函数,而只是待算法迭代结束时对输出向量ox乘以进行规整,也可使其向量成员满足约束条件但如此一来可能会引发粒子在解空间对重复解的搜索,比如对于[0.1 0.2 0.3]T和[0.2 0.4 0.6]T,显然这两者在实质上是同一个解。为了避免这一问题的出现,可以在算法的迭代过程中,通过对粒子pi的当前位置和种群中各粒子(包括pi)的历史位置进行规整,然后将规整后的当前位置与历史位置进行比较,进而实现对重复解的区分;基于此,本文在实验中采用了如下的适应度函数设计方案:
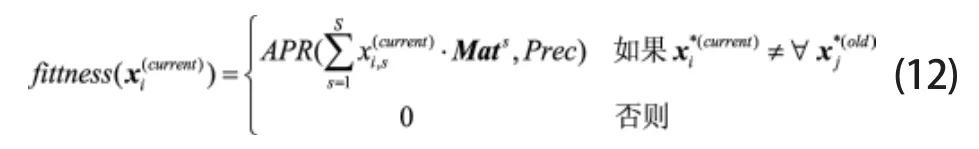
3)算法流程描述
寻找三维模型最优特征权重的算法流程如算法2所示,其中,以算法执行至最大迭代次数作为算法的终止条件。
算法2:三维模型最优特征权重的计算
输入:最优特征的类别标签集合{s};模型训练集的相似度矩阵集合{Mats},集合成员与最优特征类别相对应。
输出:最优特征权重集合{ws*}。
1)Begin;
2)初始化粒子群;
3)Do;
4)按照式(3)和式(6)分别计算粒子的位置和速度;
5)按照式(12)计算适应度,更新粒子个体极值和群体极值;
6)While未达到最大迭代次数;
7)Return {ws*};
8)End。
1.5 最优特征融合方案的使用
在查询阶段,对于给定的查询模型MQ和数据库中的候选模型MC,根据此前获取的最优特征融合方案选出相应的S种模型特征,并在此基础上按照加法规则[8]进行融合,则两个模型之间的相似度可表示为:
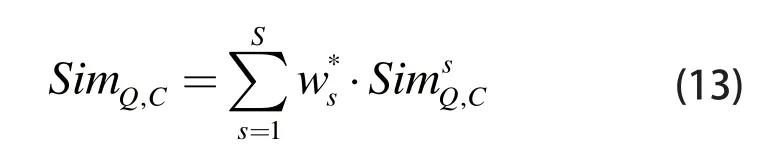
2 方法验证与讨论
为了验证所提出的多特征最优融合方法在三维模型检索中的可行性和有效性,在实验中基于4种特征提取方法,并通过参数调整获得8种不同的候选模型特征,分别是:1)基于复眼视觉算法[13]得到的SIFT特征(SSIFT);2)基于局部形状分布算法[14]得到的LSD-r0.2、LSD-r0.3、LSD-r0.5和LSD-r0.7特征(r表示算法中采样点的邻域半径);3)基于球面调和算法[5]得到的球面谐波特征(SPH);4)基于光场算法[4]得到傅立叶变换特征(FR)和Zernike矩特征(ZK)。实验模型取自美国普渡大学的Engineering Shape Benchmark(ESB)模型数据库[15]。
实验基于4个不同的检索场景展开,包括:1)棱柱类模型库——来自原数据库中的长方体-棱柱类模型;2)回转体类模型库——来自原数据库中的回转体类模型;3)自选类别模型库——来自原数据库中的齿轮、螺栓、连杆、摇杆、滑轮5个子类的模型;4)混合类模型库——来自原数据库中的模型全体。对于每一类模型资源,从中随机抽取一半模型作为训练集。

图2 部分实验模型展示
表1列出了针对各检索场景利用本文方法所得到的最优特征组合及其权重,其中“-”表示该单元格对应的候选特征未有入选。可以看出,检索场景的差异导致所适用的模型特征及其相应的权重都不尽相同,这一结果验证了在实施特征融合之前,需要首先对候选特征进行筛选,并针对性计算特征权重的必要性。值得注意的是,针对混合类三维模型的检索,8种候选特征都被选中融合,这是因为该类检索场景需要同时兼顾更多类别模型的特点,因此所需模型特征也相应增多。
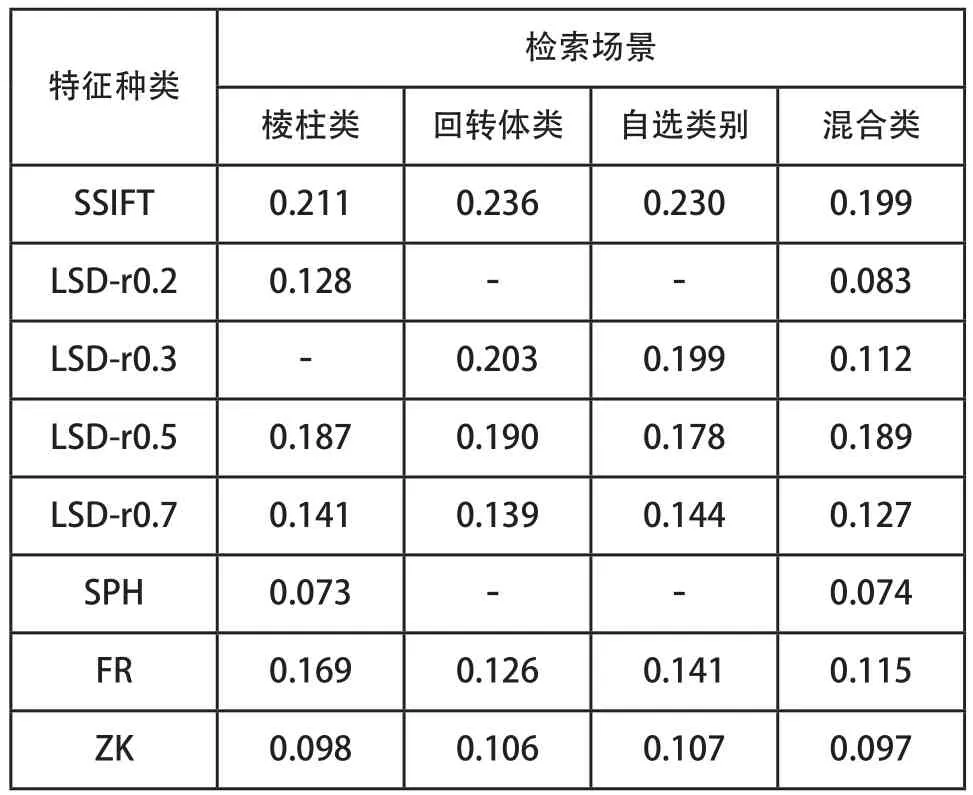
表1 针对不同检索场景的最优特征组合及权重
为了充分验证本文方法在三维模型检索中的有效性,使用信息检索领域普遍采用的查全率-查准率曲线(P-R Curve)[12]作为检索结果的评价指标,将其与另外两种多特征融合方法-基于均等权重的方法(AW)[6]和基于单值评价指标的方法(EIW)[7]进行比较。其中,AW方法对所有参与融合的模型特征都赋予相同的权重,可以看作是最大熵原理的一个应用。EIW方法借助First-tier、Second-tier等指标来设置不同特征的权重,其中使用First-tier的效果最好;相应的,本文在重复该方法时也采用了First-tier指标。需要说明的是,由于AW方法和EIW方法只针对特征权重的分配,并未涉及候选特征的筛选,因此为了确保对比的公正性,本文在重复这两种方法时都是以本文方法所选出的最优特征组合作为实验输入。
从图3中的实验结果可以看出,针对不同的检索场景,即使已给出了最适合融合的特征组合,AW方法和EIW方法仍无法在此基础上获得最好的检索结果;而由于无论是在对候选特征的筛选还是特征权重的分配上,本文方法都能做到更加合理的实施,从而与其他两种方法相比,本文方法在用于检索三维模型时的准确性表现更优。
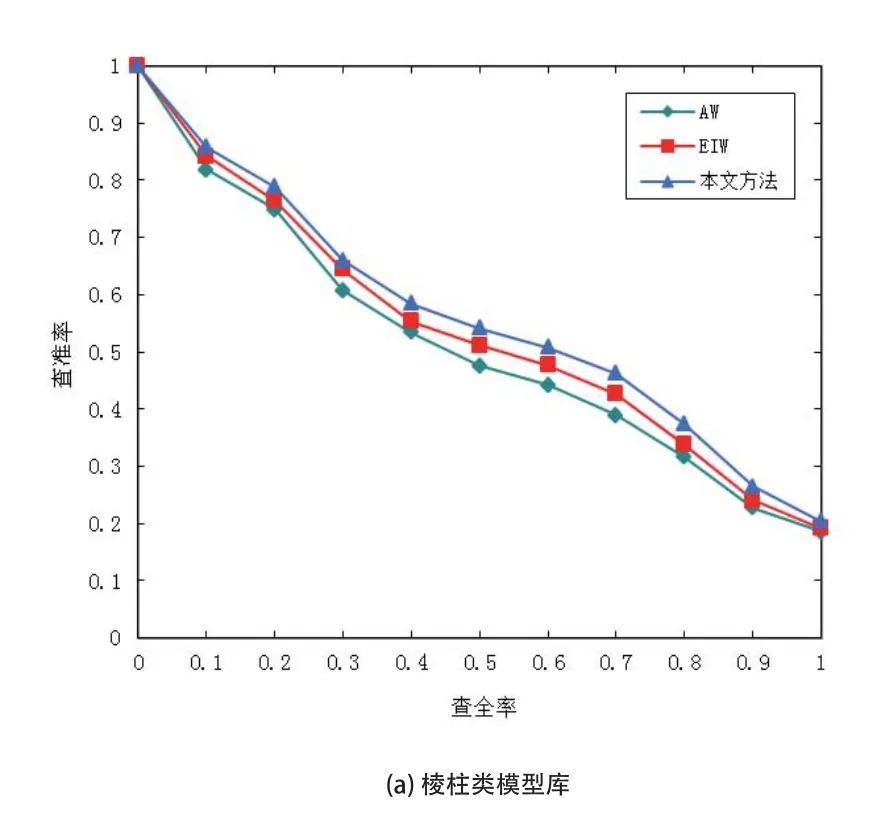
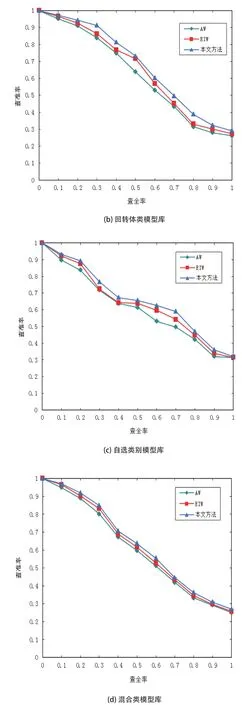
图3 三种方法针对不同检索场景的查准率-查全率表现
3 结束语
本文提出了一种三维模型的多特征最优融合方法,以提升在不同场景下对三维模型的检索效果。该方法采用监督学习的模式,利用粒子群算法从候选特征中依次完成最优特征组合的寻找和最优特征权重的计算,进而针对指定检索场景确定出最优的特征融合方案。实验结果表明,该方法能够充分迎合不同检索场景的特点,检索效果优于现有其他同类方法,能够更好地满足三维模型检索的应用需求。
[1] Johan W. H. Tangelder and Remco C. Veltkamp.A survey of content based 3D shape retrieval methods[J].Multimedia Tools and Applications,2008,39(3):441-471.
[2] Li B, Lu Y, Li C, et al. SHREC’14 Track Large Scale Comprehensive 3D Shape Retrieval[C].Eurographics Workshop on 3D Object Retrieval,Strasbourg, France,2014:131-140.
[3] Axenopoulos A, Daras P.3D Object Retrieval: Challenges and Research Directions[J].E-LETTER,2011,6(11):17-21.
[4] Chen D Y, Tian X P, Shen Y T, et al. On visual similarity based 3D model retrieval[J].Computer graphics forum,2003,22(3):223-232.
[5] Papadakis P, Pratikakis I,Perantonis S, et al. Efficient 3D shape matching and retrieval u sing a concrete radialized spherical projection representation[J].Pattern Recognition,2007,40(9): 2437-2452.
[6] Li B, Johan H. 3D model retrieval using hybrid features an d class information[J].Multimedia tools and applications.2013,62(3):821-846.
[7] 万丽莉,刘美琴.基于评价指标组合特征的三维模型检索方法[J].计算机辅助设计与图形学学报.2009,21(11):1563-1568.
[8] He M, Horng S, Fan P, et al. Performance evaluation of score level fusion in multimodal biometric systems[J].Pattern Recognition. 2010,43(5):1789-1850.
[9] Elbeltagi E, Hegazy T,Grierson D.Comparison among five evolutionary-based optimization algorithms[J].Advanc ed engineering informatics,2005,19(1):43-53.
[10] Blum C,Merkle D.Swarm intelligence: introduction and applications[M].Springer Berlin Heidelberg,2008:59-64.
[11] 许金友,李文立,王建军.离散粒子群算法的发散性分析及其改进研究[J].系统仿真学报,2009,21(15):4676-4681.
[12] Manning, Christopher D., Prabhakar Raghavan, and Hinrich Schütze. Introduction to information retrieval[M].Cambridge university press,2009:160-161.
[13] Li L, Zhang S, Bai X and Shao Li. Retrieving 3D models using compo u nd-eye visual representations[C].in Proceedings of 13th IEEE International Conference on Computer-Aided Design and Computer Graphics,2013:172-179.
[14] 李亮, 张树生,白晓亮,黄瑞.一种三维CAD模型自动语义标注算法[J].计算机集成制造系统,2013,19(7):1484-1489.
[15] Shapelab.ecn.purdue.edu[DB].
3D model retrieval using a multi-feature fusion method
LI liang1, BAI Xiao-liang2, WEI Qing-yan1
TP391
:A
1009-0134(2017)03-0005-06
2016-11-13
中国空空导弹院青年创新基金资助项目(CQKJJ00-2016-18);西北工业大学民口重大项目培育资助项目(3102015BJ(II)MYZ21);国家自然科学基金资助项目(51175434)
李亮(1983 -),男,山东济南人,工程师,博士,主要从事三维模型检索技术和智能制造技术研究。

