基于线性约束最小方差的脑磁源定位特性研究

陈志阳，黄丽亚，文 念，笪铖璐，吴劲松

(南京邮电大学 电子科学与工程学院，江苏 南京 210023)

基于线性约束最小方差的脑磁源定位特性研究

陈志阳，黄丽亚，文 念，笪铖璐，吴劲松

(南京邮电大学 电子科学与工程学院，江苏 南京 210023)

波束形成是一种广泛运用于脑磁信号的偶极子溯源方法，其定位结果的准确度是目前研究的一个关键点。基于电流偶极子模型，以相关系数和定位误差作为评价标准，研究了不同头模型、不同伪迹噪声对线性约束最小方差定位算法的影响。通过计算机软件，在脑内已知位置设定已知源信号，采用不同头模型进行前向问题计算并叠加不同噪声，对模拟的真实脑磁信号进行逆问题的求解，进行源定位与源信号重构。仿真结果表明，在叠加相同噪声的情况下，采用不同头模型在较低信噪比下对算法的影响有一定差异，而在信噪比高于-10分贝的条件下，则对算法几乎没有影响，能达到较好的定位效果。在采用相同头模型的情况下，叠加不同类型的噪声伪迹所产生的影响各不相同，其中高斯白噪声产生的影响最大，有色噪声次之，基线漂移产生的影响最小。

脑磁信号；源定位；头模型；线性约束最小方差；噪声

1 概 述

脑磁信号(Magnetoencephalography，MEG)是脑外记录的脑内神经电流发出的极其微弱的生物磁场信号。根据脑外磁场反演脑内神经活动源的分布情况，称为MEG源定位，即MEG反向问题，对临床神经科学和脑功能研究有着重要意义。为了实现MEG源定位，要设定源的分布及头模型的几何结构和媒质参数，求解出头皮电位，即MEG前向问题，它直接影响源定位的求解结果，其中头模型的选择至关重要。Lalancette等[1]将单球模型和局球模型进行比较时采用基于边界元方法(Boundary Element Method，BEM)的真实模型作为参照，但所比较头模型均为球形模型，使比较具有一定的局限性。李璟等[2]通过比较前向问题的解析解与数值解从而对模型进行分析和评价，不过对于复杂头模型，无法得到其解析解。Henson等[3]使用自由能近似贝叶斯模型的方法来比较各种头模型的构造结果。Mideksa等[4]分析了不同头模型和导联类型对定位γ波段振荡的影响，发现局部球模型比单壳模型的定位结果更加集中，但没有分析更加复杂的头模型。吴占雄等[5]讨论了各种非均质电导率对脑电正问题的影响，但是没有考虑噪声对源定位结果的影响。

当前常见的源定位方法包括动态统计参数映射(DSPM)、线性约束最小方差(LCMV)波束形成器(Beamforming)、混合模估计(MxNE)[6]和合成孔径磁场定位法(SAM)等[7]。上述算法中噪声是影响定位效果的重要因素，因为一般情况下，噪声的强度非常强，远远大于源定位。因此多数MEG定位算法都需要在高信噪比情况下才能得出较好的结论[8]，而且，为了简化计算，往往把噪声设定为高斯白噪声[9-11]。然而真实测得的MEG信号中大量的噪声伪迹成分，如眼电伪迹、肌电伪迹、心电伪迹等都不属于高斯白噪声，因此仅仅研究高斯白噪声的影响必然会产生较大的偏差。

基于含有多种噪声的脑磁研究已经受到较多关注，文献[12]用韧性时频分析方法实现对强脉冲噪声环境下的新生儿脑电时频分析，体现了良好的时频效果。对于脑磁伪迹的消除，研究者提出过回归方法[13]、伪迹减法[14]、小波变换[15]、主成分分析[16]和独立成分分析等[17]。然而不同噪声环境、不同头模型对源定位的影响在当前的文献中研究较少。

真实采集到的MEG信号中含有多种噪声，采用上述去噪方法，很难保证针对不同类型的噪声均有较好的去噪效果。文献[18]为了获得具有较高信噪比的信号，提出了一种使用计算机模生成的功能性磁共振成像(functionalMagneticResonanceImaging,fMRI)数据，对脑电信号进行融合处理的方法。

基于电流偶极子模型，重点研究多种头模型、多种噪声源对MEG源定位和源信号重构的影响。通过计算机软件，在脑内已知位置设定已知源信号，基于源模型、头模型和传输参数进行前向计算，并叠加多种常见伪迹噪声来模拟真实的MEG信号，采用LCMV波束形成算法进行源定位与源信号重构并进行仿真分析。

2 研究方法

2.1 前向问题

MEG前向问题需要构造合适的头模型和源模型来建立脑内信号源与脑外电磁场之间的联系。Brazier在1949年提出的电流偶极子模型作为脑内激励源被广泛应用[19]，后续仿真采用了电流偶极子模型作为源模型。对于模拟人脑的头模型，采用了4种具有代表性的模型：无限空间(infinite)模型、单球(single-sphere)模型、局部球(local-sphere)模型和单壳(single-shell)模型。

大脑通常被近似为无源、均匀且各向同性的介质，脑内生理活动规律可以用准静态的麦克斯韦方程(Maxwell’s Equations)来描述[20]，脑内电流源J由原电流(primary)JI和体积电流(passive)JV两部分组成，可表示为J=JI+JV。其中，原电流为细胞内电流，体积电流为电流经过大脑的其他部分。体积电流JV满足JV=σE，其中σ为电导率，E为电场(E=-V，V为电势)。由旋度的性质可知：

(1)

对于给定原电流JI，可唯一确定V，进而求出总电流J。

(1)无限模型。

设人脑的磁导率为常数μ0，在电流偶极子模型下，根据Biot-Savart定理，在无限均匀和各向同性的容积导体中，位于r处具有偶极矩Q的激励源，在r′处产生的磁感应强度可表示为[20]：

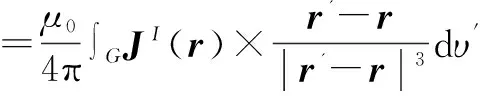
(2)

若L为MEG导联在位置r'处测得的方向为n的前向电场(leadfield)，则满足[21]：

n·B(r')=∫d3rJI(r)·L(r,r',n)

(3)

基于上述理论，Nolte[21]等将头部划分成白质、灰质、头骨和头皮等部分，结合高斯定律(Gaussianlaw)和散度旋度定理，可以得出在不同脑组织的分界面上满足：

σ-n·U-(r)-σ+n·U+(r)=

(σ--σ+)n·L∞(r)

(4)

其中,σ-(σ+)为分界面内(外)电导率;U-(U+)为对应的前向电场电位;r为两种脑组织分界面上的点。

(2)单球模型[21]。

球模型是最早也是最简单的模型，即把头看成各向同性、电导率均匀的介质球。假设Ω是有边界的球对称导体，S是单球表面，脑外电导率σ=0，脑内电导率σ=σ0。结合式(1)和式(2)，对位于r处且具有偶极矩Q的偶极子，在r'处产生的磁感应强度可表示为：

B(r')=B∞(r')+

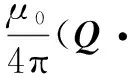
(5)

其中，B∞为无限均匀各向同性容积导体的磁感应强度。

n·B(r')=Q·L(r,r',n)=Q·L∞(r,r',n)-Q·U(r,r',n)

(6)

其中，L∞为在一个无限均匀各向同性容积导体中的前向电场。

(3)单壳模型[21]。

单壳模型属于真实头模型。对于特定的导联，单壳模型的前向电场可写为：

L(r)=Lsph(r)-u(r)

(7)

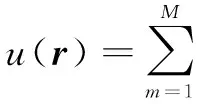
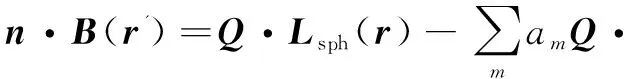
(8)

(4)局部球模型[22]。

局部球模型是单球模型的一个扩展，它是对每个MEG导联拟合一个球模型，在保留了球模型计算效率的同时还保证了近似于BEM模型的准确度，但这种方法存在的问题是MEG导联所在区域的面积难以准确界定的。文献[23]提出了解决思路：假定颅骨是完全绝缘的，则可以仅估算最里层的颅骨表面积分，从而降低计算复杂度。采用含有N个点的表面网格表示最里层的颅骨表面，则位于r处且方向为o的MEG导联，其最小二乘法拟合的问题可简化为最小化代价函数的问题：

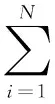
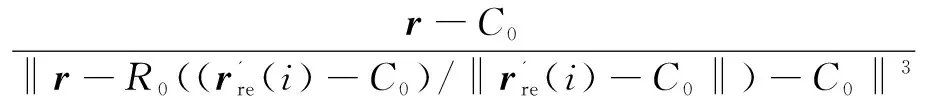
(9)

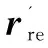
采用NelderandMead(1965)的单纯形法(thesimplexmethod)反复调整各参数，使上述代价函数最小化，对每个MEG导联重复上述步骤得到一组重叠球。

2.2 反向问题—LCMV定位

MEG反向问题具有不适定性(ill-posed)，用脑外采集到的MEG信号反演脑内激励源，存在无数个解，从而导致了反向问题的研究颇具难度，目前大部分算法都采用了不同假设来突破这一限制，比如需要事先假定已知激励源的数目[24]。研究采用的线性约束最小方差(LCMV)Beamforming方法可以避免上述假设[25]。它将脑外所记录信号看作是各活动神经元产生信号的线性叠加，则由多个导联采集到的、叠加了噪声的测量MEG信号x(t)可用以下模型表示：

x(t)=L(q)·s(t)+N(t)

(10)

其中，L(q)=[l(q1),l(q2),…,l(qr)]为不同位置qi(i=1,2,…,r)处的偶极子源与MEG导联形成的前向矩阵，在前向问题中计算得出；s(t)和N(t)则分别表示源和噪声。

若已知s(t)，则可通过等式x0(t)=L(q)·s(t)前向计算出x0(t)。波束形成方法实际上是寻求一个空间滤波权W(q0)，以便通过在q0位置的信号，阻止其他位置信号。滤波器的输出用y表示，则所测MEG经波束形成空间滤波器输出为：

y=WT(q0)x

(11)

则LCMV问题可简化为：在所有可行的空间滤波权中，选择一种使输出方差最小的W(q0)：

(12)

利用拉格朗日算子可得到W(q0)：

W(q0)=[LT(q0)C-1(x)L(q0)]-1LT(q0)C-1(x)

(13)

所求得的q0为估计源位置，将所求的W(q0)代入式(11)即可求得源的波形。

3 仿真实验

3.1 MEG模拟数据

实验采用151导联的CTF system MEG测量系统。模拟的电流偶极子源q的坐标为(0.8，3.2，3.4)，源空间是一个基于真实被试的MRI扫描图，整个脑被划分成了11 000个网格点。采用时间函数s(t)来模拟偶极子激励源，如图1(a)所示：

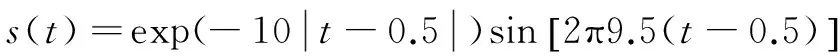
(14)

基于4种头模型，求解前向问题分别得到头皮电位。然后叠加6种噪声或伪迹，分别为：高斯白噪声(WhiteNoise，WN)、有色噪声(ColoredNoise，CN)、肌电运动伪迹(MuscleArtifacts，MA)、电极运动伪迹(ElectrodeMovements，EM)、基线漂移伪迹(BaselineWander，BW)、几种伪迹的混合伪迹(MX)。图1(b)显示了单壳(single-shell)模型下，叠加5dB的混合伪迹后的MEG导联波形图。

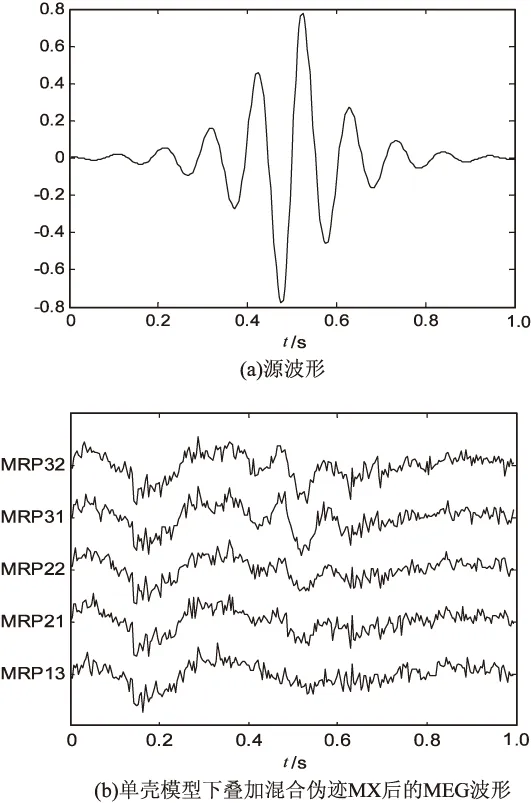
图1 模拟源设置

3.2 MEG溯源仿真

采用LCMV方法对叠加噪声后的MEG进行反向问题求解，可完成源定位和源信号重构。仿真将采用溯源得到的源位置坐标和源信号波形与实际信号源进行比较，采用定位误差(LB)和Pearson相关系数[26](CR)作为评估参数:

(15)

(16)

其中，(xq,yq,zq)表示已知源q的坐标位置；(xq0,yq0,zq0)表示重建源q0的坐标位置。LB越小则定位越准确；CR(s,y)中s表示源信号，y表示经空间滤波器重建的信号，CR越大表明两信号之间线性相关性越强，信号重构程度越好。

对图1(b)中单壳模型下叠加5dB的MX得到的模拟MEG，采用LCMV算法进行定位。在源能量成像分布图中，将能量最大处的位置确定为重建源所在位置，进而重建该处源的波形图，如图2所示。

图2 重建源的定位

图2中所示的重建源位置为(0.9，3.22，3.43)，与设定源位置(0.8，3.2，3.4)相比，定位误差为0.114cm；将重建波形与设定源波形进行相关计算，CR为99.73%。

对4种头模型得到的MEG分别叠加6种噪声信号，总共可产生24组MEG数据，分别对它们进行LCMV定位与源信号重构，采用评估参数分析得到的结果。

图3显示了不同噪声背景下相关系数CR与信噪比(SNR)的关系曲线，每幅图包含了4种头模型对CR的影响。

从图3中可看出，随着SNR的增加，CR总体呈上升趋势，当达到某一个SNR阈值时，相关系数大幅增加，可达80%以上。同一类噪声下尽管采用不同的头模型，得到的SNR阈值几近相同，其中白噪声下的SNR阈值为-15dB,机电伪迹下的SNR阈值为-40dB，也表明在高信噪比下，不同头模型对溯源结果影响不大。

图4则显示了定位误差(LB)与SNR的关系曲线。随着SNR的增加，LB总体呈下降趋势。在同一噪声下，当信噪比达到一定程度时，头模型对LB的影响可以忽略。但在不同的噪声环境下，达到LB阈值(设阈值为1cm)时的SNR也不相同。

在不同类型噪声背景下，当信噪比程度低于对应SNR阈值时，可以认为源信号重建不可靠。达到稳定时所对应的SNR值越大，说明噪声的影响越大，反之越小。

图5显示了达到评估参数阈值(CR=80%,LB=1cm)时不同噪声的SNR阈值，分别为-10dB(WN)、-15dB(CN)、-35dB(MA)、-50dB(EM)、-60dB(BW)、-40dB(MX)。可以看出，不同类型噪声对MEG反向问题求解有不同的影响，其中基线漂移伪迹的影响最小，高斯白噪声的影响最大，有色噪声的影响也不能忽略，而总体来说LCMV定位方法在信噪比高于-10dB的噪声背景下的定位效果较好。

进行另一组模拟电流偶极子源的参数设置，源信号为s(t)=sin2π10t，源位置q为(4.36，-3.78，-0.56)。对在单壳模型下叠加5dB的MX所得到的模拟MEG，采用LCMV算法进行定位。重建源位置为(4.36，-4.58，-0.61)，与设定的源位置(4.36，-3.78，-0.56)相比，定位误差为0.8cm；将重建波形与设定源波形进行相关计算，CR高达99.67%。

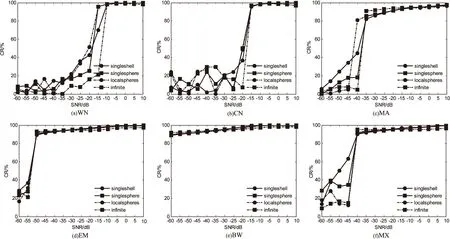
图3 不同噪声和头模型下CR与SNR的关系曲线

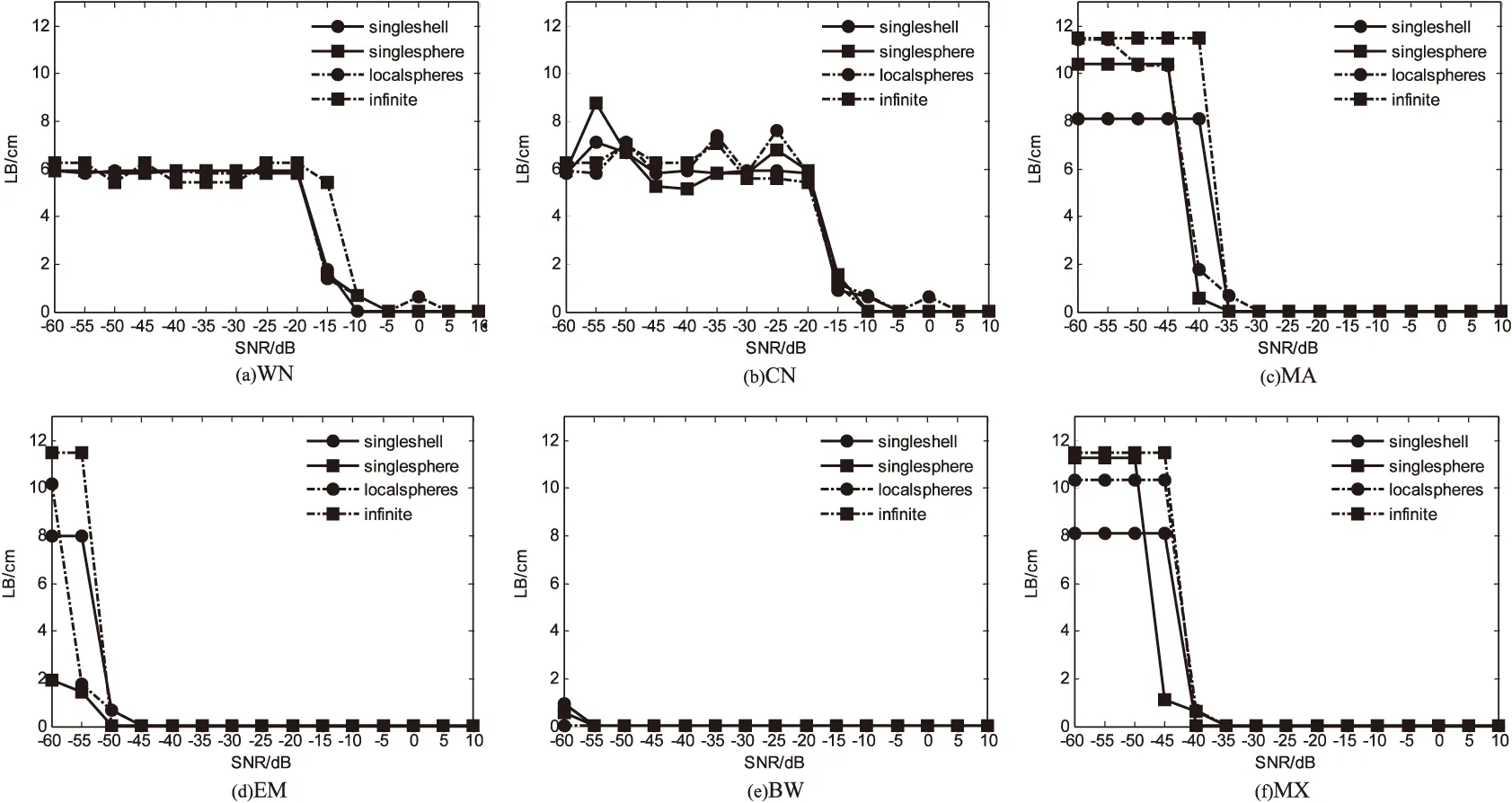
图4 不同噪声和头模型下LB与SNR的关系曲线

图5 不同类型噪声背景下定位结果 达到稳定时的SNR值

随后，在此模拟源设定下继续对4种头模型得到的MEG记录分别叠加6种噪声信号，对产生的24组MEG数据进行LCMV定位与重建，可以得到相似的结论。

4 结束语

基于电流偶极子模型，研究了多种头模型、多种噪声源对MEG源定位和源信号重构的影响。采用LCMV方法进行反向问题求解，以相关系数和定位误差作为评价标准，分析了MEG源定位与重建的效果。仿真结果表明，在叠加相同噪声的情况下，采用不同头模型在较低信噪比下对算法的影响有一定差异，而在信噪比高于-10dB的条件下，则对算法几乎没有影响，能达到较好的定位效果。在采用相同头模型的情况下，叠加不同类型的噪声伪迹所产生的影响各不相同，其中高斯白噪声产生的影响最大，有色噪声次之，基线漂移产生的影响最小。以上结论可为脑磁源定位提供参考，有效地提高源定位算法的准确性。

[1]LalancetteM,QuraanM,CheyneD.Evaluationofmultiple-sphereheadmodelsforMEGsourcelocalization[J].PhysicsinMedicineandBiology,2011,56(17):5621.

[2] 李 璟,李重视,张迎春,等.FEM与FDM在脑电正问题求解中的比较[J].浙江大学学报:工学版,2008,42(4):647-650.

[3]HensonRN,MattoutJ,PhillipsC,etal.SelectingforwardmodelsforMEGsource-reconstructionusingmodel-evidence[J].Neuroimage,2009,46(1):168-176.

[4]MideksaKG,HoogenboomN,HellriegelH,etal.Impactofheadmodelingandsensortypesinlocalizinghumangamma-bandoscillations[C]//36thannualinternationalconferenceonengineeringinmedicineandbiologysociety.[s.l.]:IEEE,2014:2217-2220.

[5] 吴占雄,李 璟,朱善安.脑白质电导率各向异性及非均质对头皮脑电分布的影响[J].传感技术学报,2010,23(11):1523-1527.

[6]EngemannD,StrohmeierD,LarsonE,etal.MindthenoisecovariancewhenlocalizingbrainsourceswithM/EEG[C]//Internationalworkshoponpatternrecognitioninneuro-imaging.[s.l.]:IEEE,2015:9-12.

[7] 赵铁柱,关 卉,郑 罡,等.合成孔径磁场模型在脑磁图场源定位中的应用[J].临床神经外科杂志,2014,11(1):73-75.

[8]MosherJC,LeahyRM.Sourcelocalizationusingrecursivelyappliedandprojected(RAP)MUSIC[J].IEEETransactionsonSignalProcessing,1999,47(2):332-340.

[9] 朱红毅,李 军,罗 斌.真实头模型中的多电流偶极子脑磁源定位[J].物理学报,2002,51(10):2393-2398.

[10]MohseniHR,KringelbachML,WoolrichMW,etal.Non-GaussianprobabilisticMEGsourcelocalisationbasedonkerneldensityestimation[J].NeuroImage,2014,87:444-464.

[11]EngemannDA,GramfortA.AutomatedmodelselectionincovarianceestimationandspatialwhiteningofMEGandEEGsignals[J].NeuroImage,2015,108:328-342.

[12]PatarinJ.HiddenFieldsEquations(HFE)andIsomorphismsofPolynomials(IP):twonewfamiliesofasymmetricalgorithms[M]//AdvancesinCryptology.Berlin:Springer,1996:33-48.

[13]KenemansJL,MolenaarPCM,VerbatenMN,etal.RemovaloftheocularartifactfromtheEEG:acomparisonoftimeandfrequencydomainmethodswithsimulatedandrealdata[J].Psychophysiology,1991,28(1):114-121.

[14]GirtonDG,KamiyaJ.Asimpleon-linetechniqueforremovingeyemovementartifactsfromtheEEG[J].Electroencephalography&ClinicalNeurophysiology,1973,34(2):212-216.

[15] 李海东,李 青.基于阈值法的小波去噪算法研究[J].计算机技术与发展,2009,19(7):56-58.

[16]BergP,SchergM.DipolemodellingofeyeactivityanditsapplicationtotheremovalofeyeartefactsfromtheEEGandMEG[J].ClinicalPhysics&PhysiologicalMeasurement,1991,12:49-54.

[17]BellAJ,SejnowskiTJ.Aninformation-maximizationapproachtoblindseparationandblinddeconvolution[J].NeuralComputation,1995,7(6):1129-1159.

[18] 张少白,王 勇,刘友谊.基于DIVA模型的脑电信号处理方法研究[J].计算机技术与发展,2016,26(8):152-155.

[19]BrazierMAB.Astudyoftheelectricalfieldsatthesurfaceofthehead[J].Electroenceph.Clin.Neurophysiol.,1949,2:38-52.

[20]SarvasJ.Basicmathematicalandelectromagneticconceptsofthebiomagneticinverseproblem[J].PhysicsinMedicineandBiology,1987,32(1):11-22.

[21]NolteG.Themagneticleadfieldtheoreminthequasi-staticapproximationanditsuseformagnetoencephalographyforwardcalculationinrealisticvolumeconductors[J].PhysicsinMedicineandBiology,2003,48(22):3637-3652.

[22]HuangMX,MosherJC,LeahyRM.Asensor-weightedoverlapping-sphereheadmodelandexhaustiveheadmodelcomparisonforMEG[J].PhysicsinMedicineandBiology,1999,44(2):423.

[23]HamalainenMS,SarvasJ.Realisticconductivitygeometrymodelofthehumanheadforinterpretationofneuromagneticdata[J].IEEETransactionsonBiomedicalEngineering,1989,36(2):165-171.

[24]SchergM.FromEEGsourcelocalizationtosourceimaging[J].ActaNeurologicaScandinavicaSupplementum,1994,89(S152):29-30.

[25]DmochowskiJ,BenestyJ,AffesS.Linearlyconstrainedminimumvariancesourcelocalizationandspectralestimation[J].IEEETransactionsonAudio,Speech,andLanguageProcessing,2008,16(8):1490-1502.

[26]ColeMW,PathakS,SchneiderW.Identifyingthebrain'smostgloballyconnectedregions[J].Neuroimage,2010,49(4):3132-3148.

Investigation on MEG Source Localization with Linear Constrained Minimum Variance

CHEN Zhi-yang，HUANG Li-ya，WEN Nian，DA Cheng-lu，WU Jin-song

(College of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

Beamforming is widely used in the dipole sourcing for magnetoencephalography (MEG) signals,and the accuracy of localization result is the key of the current research.Based on the current dipole source model,the influence of different head models and artifacts on the Linear Constrained Minimum Variance (LCMV) sourcing has been discussed,taking the correlation and the localization bias as the valuation criteria.The source signal has been simulated using computer software and the forward problem has been solved based on different head model,then the inverse problem is calculated to localize the sources and reconstruct the signals under different noise environments.The simulation suggests that under the same noise environment,the localization result has been affected by the head model while the signal to noise ratio is low,however the accuracy of localization result is more reliable and not related to the head model when the SNR is higher than -10dB.In the case of the same head model,the types of artifacts lead to different results,where Gaussian white noise has the greatest influence,colored noise is second,and baseline wander artifact has the least influence.

MEG;source localization;head model;LCMV;noise

2016-05-30

2016-09-08

时间：2017-03-07

国家自然科学基金资助项目(61271334)

陈志阳(1992-)，男，硕士生，研究方向为脑磁源定位和脑功能网络分析；黄丽亚，教授，硕士生导师，研究方向为脑电信号的分析和处理以及通信网络的QoS性能。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0922.060.html

TP391;TM152

A

1673-629X(2017)04-0170-06

10.3969/j.issn.1673-629X.2017.04.038