抛掷硬币方案研究

马 丽，窦家维，吴艳梅

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

抛掷硬币方案研究

马 丽，窦家维，吴艳梅

(陕西师范大学 数学与信息科学学院，陕西 西安 710119)

抛掷硬币是多方保密计算的一个重要模块，而且在现实生活中也有重要应用。网络中，抛掷硬币的双方往往不在同一个地点，但仍需要公平地决定一件事情，因而抛掷硬币的公平性是一个重要的研究方向。可见，无论是计算机及网络保密，还是日常生活，都需要研究和解决抛掷硬币的不公平问题。为此，在应用单向函数构建一个公平的抛掷硬币方案，并验证其有效性的基础上，采用二次剩余法和勒让德符号设计了一个不公平的抛掷硬币方案，正面朝上的概率为0.25，反面朝上则为0.75。在网络通信前提下,对两种方案的安全性和复杂性分别进行了对比分析研究。分析结果表明，所设计的两种抛掷硬币方案将单向函数与抛掷硬币协议有机结合，相关协议简单易行，具有较好的应用价值。

密码学；多方保密计算；硬币抛掷；离散对数假设

1 概 述

随着网络信息技术的发展，网络不仅给人们的日常生活带来许多便捷，同时也存在诸多隐患。有些网络用户可能出于经济目的、政治目的或者个人目的等，利用网络中的漏洞对其实施攻击，造成网络信誉下降、丧失机密等网络安全事故，严重地可能造成国家政治、社会、经济的混乱；因此，信息安全问题是当今社会急需解决的课题之一[1-5]。文中主要以抛掷硬币问题为主，设计一种简单、可行、有效的安全协议。

抛掷硬币方案是密码学中一个重要的研究方向。Blum在1982年利用调制解调器提出抛掷公平硬币问题[6]，利用位比特协议解决两个人抛掷硬币问题；Ben等在1990年提出了硬币抛掷问题[7]；佘堃在2003年提出了公平硬币抛掷协议[8]，随后许多学者对抛掷硬币方案进行了研究[9-13]。

在信息化时代，人们仍需要用抛硬币的方法公平地决定某件事，比如：足球比赛前，主裁判在场地中央抛掷硬币，决定哪一方先发球。但是如果在网络活动中，两个人需要通过抛硬币的方法决定一件事就困难了，因为他们处在世界的不同角落，不可能因为抛硬币走在一起。而如果其中一个人抛硬币，假设选择由Alice抛硬币，Bob担心两件事：一是Alice选择硬币可能是不均匀的，可能出现正面的情况多，或者出现反面的情况多；二是即使Alice选择的硬币是均匀的，但是Alice可能不报告抛掷的正确结果，而选择一个对自己有利的结果。在密码学中，甲乙抛掷硬币，结果揭示之前，双方都不想让对方知道自己的结果，这是多方保密计算的重要模型之一。历史上许多学者进行了抛硬币实验，并且推动了硬币实验在密码学和信息安全中的重要应用，但是仍然存在许多不足。生活中有这样的事情:两个人为一件小事争执不休，他们用抛掷硬币的方式解决，他们不能亲眼见证抛掷结果，只能相互告知。

文中利用单向函数设计了一个公平的抛掷硬币方案，使得正面向上的概率为0.25，反面向上的概率为0.75，并分析了两种方案的安全性。

2 预备知识

2.1 二次剩余

定义1：设n是正整数，若同余式x2≡a(modn),(a,n)=1有解，则a叫模n的二次剩余，否则a叫模的非二次剩余。

定义2：设p是素数，定义勒让德符号(Legender)如下[14]：

(1)

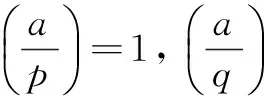
2.2 离散对数假设

αx≡βmodp

(2)

(3)

2.3 设计原则

在设计抛掷硬币协议的过程中需满足以下性质：

(1)Alice必须在Bob猜测之前抛掷硬币。

(2)在听到Bob的猜测后，Alice不能再抛掷硬币。

(3)Bob在猜测之前不能知道硬币是怎么落地的。

2.4 基于公开密钥密码术的抛币协议

协议设计原理：该协议可以与公开密钥系统又可与对称密码系统一起工作。其唯一要求就是满足交换律。一般对对称算法这个特性不满足，但对某些公开密钥算法是正确的。

协议1：基于公开密钥密码术的抛币协议[14]。

(1)Alice和Bob都产生一个公开密钥/私人密钥对。

(2)Alice产生两个消息，其一指示正面，另一个指示反面。这些消息中包含有某个唯一的随机串，以便以后能够验证其在协议中的真实性。Alice用她的公开密钥加密两个消息，并以随机的顺序把他们发给Bob：EA(M1),EA(M2)。

(3)Bob由于不能读懂其中任意一条消息，于是随机选择一条，用他的公开密钥加密并回送给Alice：EB(EA(M))(M为M1或M2)。

(4)Alice由于不能读懂送回给她的消息，就用她的私人密钥解密并发送给Bob：DA(EB(EA(M)=EB(M1)(M=M1)或EB(M2)(M=M2)。

(5)Bob用他的私人密钥解密消息，得到硬币的结果。将解密后的消息发给Alice：DB(EB(M1))=M1或DB(EB(M2))=M2。

(6)Alice得到抛硬币结果，并验证随机串的正确性。

(7)Alice和Bob出示他们的密钥对以便双方能验证对方没有欺骗。

安全性分析如下：

这个协议是自我实施的。任意一方都能即时检测对方的欺诈，不需要可信的第三方介入实际的协议和协议完成后的仲裁。如果试图欺诈，看看协议是如何工作的。

如果Alice想欺骗，强制为正面，她有三种可能的方法影响结果。首先，可以在步骤(2)中加密两个“正面”的消息。在步骤(7)Alice出示她的密钥时，Bob就可以发现这种欺骗。第二种方法，Alice在步骤(4)用一些其他的密钥解密消息，将产生一些乱七八糟的无用消息，Alice可在步骤(5)中发现。第三种方法，Alice可在步骤(6)中否认消息的有效性，当在步骤(7)中Alice不能证明消息无效，Bob就可以发现。当然，Alice可以在任何一步拒绝参与协议，那样，Alice欺骗Bob的企图就显而易见了。

如果Bob想欺骗并强制为“反面”，他的选择性不大。他可以在步骤(3)中不正确地加密一条消息，但Alice在步骤(6)查看最终的消息时就可以发现；他可以在步骤(5)中进行不适当的操作，但这会导致乱七八糟的无用信息，Alice可在步骤(6)中发现；他可以声称由于Alice那方的欺诈使他不能适当地完成步骤(5)的操作，但这种形式的欺诈能在步骤(7)中发现；最后，他可能在步骤(5)中给Alice一个“反面”的消息，而不管他解密获得的消息是什么，但Alice能在步骤(6)中立即检验消息的真实性。

3 问题与解决方案

3.1 基于离散对数的公平抛掷硬币协议

协议设计原理：Alice和Bob一致选择y≡axmodp作为协议中的单向函数，利用x的奇偶性，可以实现公平的抛掷硬币的方案。

协议2：Alice和Bob一致选择y≡axmodp作为协议中的单向函数。

(1)Alice选择一个非零的随机数x，并计算y≡axmodp。

(2)Alice将y发送给Bob。

(3)Bob猜测x是奇数还是偶数，并将猜测结果发送给Alice。

(4)如果Bob的猜测结果正确，则抛硬币的结果为正面；如果Bob的猜测结果错误，则抛硬币的结果为反面。Alice公布此次抛硬币的结果，并将x发送给Bob。

(5)Bob验证y≡axmodp。

安全性分析如下：

在抛掷硬币的过程中，只有Alice可能进行欺骗，因为在协议过程中，Bob只是猜测。

如果Alice在步骤(2)进行欺骗，发送y′(y′≠y)给Bob，Bob在步骤(5)计算y≡axmodp，可检验Alice是否进行欺骗。

如果Alice在步骤(4)进行欺骗，发送x′(x≠x′)给Bob，Bob在步骤(5)计算y≡axmodp，可检验Alice是否进行欺骗。

3.2 基于二次剩余的不公平抛掷硬币协议

协议设计原理：Alice和Bob利用二次剩余的原理，以及勒让德符号，实现了不公平的抛掷硬币方案。

协议3：Alice和Bob抛掷硬币，猜测值为a。

(1)Alice选择两个不同的大素数p,q，并计算n=pq，将n发送给Bob。

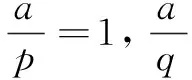
(3)Alice将步骤(2)的验证结果告诉Bob，并将p,q发送给Bob。

(4)Bob验证p,q是否为两个不同的大素数，且验证n=pq是否成立。

安全性分析如下：

在抛掷硬币的过程中，只有Alice可进行欺骗，因为Bob是一个验证者的身份。假设Alice进行欺骗。

Alice在步骤(1)进行欺骗，Bob在步骤(6)对n=pq进行验证，根据因子分解原理，可得到Alice是否进行欺骗。

Alice在步骤(3)进行欺骗，将错误结果和p,q发给Bob，Bob在步骤(6)对n=pq进行验证，根据因子分解原理，可得到Alice是否进行欺骗。

4 性能分析

协议1为基于公开密钥密码术的抛硬币协议，但只适合于某些公开密钥算法，如相同模数的RSA算法；协议2为基于单向函数的抛硬币协议，弥补了协议1的不足；协议3为基于二次剩余的抛硬币协议，突破了一般的公平抛硬币协议，使得正面的概率为0.25，反面的概率为0.75。现对这三种协议的计算复杂性和通信复杂性进行分析。

4.1 计算复杂性

在利用公钥密码系统构建的协议中，模指数运算的次数是决定协议效率的主要因素，因此协议的计算复杂性由模指数运算的次数衡量。如果一个协议中进行模指数运算的次数越多，其计算复杂性越高，所以把模指数运算作为对这三种协议进行计算复杂性分析的主要方面。协议2需要进行2次模运算，而协议1和协议3无需模指数运算，协议3实现了不公平的抛掷硬币。

4.2 通信复杂性

协议的通信复杂性是传递数据的次数或者传送数据的比特数。传递的次数越多，则协议的通信复杂性越高。协议1中，通过4次传递完成了数据的交互过程。协议2中，通过3次传递完成了数据的交互过程。协议3中，通过2次传递完成了数据的交互过程。很明显，协议3的计算复杂性较低。

5 结束语

文中提出了两种新的抛硬币协议，基于单向函数的方案和基于二次剩余的方案。协议2简单易行；协议3突破了传统的公平抛硬币协议，使得正面的概率为0.25，反面的概率为0.75。对协议2和协议3的安 全性和复杂性进行了分析，并与协议1进行了对比。

在满足抛硬币协议设计原则的基础上，如何设计出简单公平的抛硬币协议是今后主要研究的对象。

[1] Beimel A,Omri E, Orlov I.Protocols for multiparty coin toss with a dishones majority[J].Journal of Cryptology,2015,28(3):551-600.

[2] Moran T,Naor M,Segev G.An optimally fair coin toss[J].Journal of Cryptology,2016,29(3):491-513.

[3] Diaconis P,Holmes S,Montgomery R.Dynamical bias in the coin toss[J].SIAM Review,2007,49(2):211-235.

[4] Turner B J,Hecht F M.Improving on a coin toss to predict patient adherence to medications[J].Annals of Internal Medicine,2001,134(10):1004-1006.

[5] Cho A.Breakthrough lost in coin toss[J].Science,2014,346(6205):22-23.

[6] Blum M.Coin flipping by telephone:a protocol for solving impossible problems[C]//Proceedings of the 24th IEEE computer conference.[s.l.]:IEEE,1982:133-137.

[7] Benor M,Linial N.Collective coin flipping[J].Randomness and Computation,1990,5:91-115.

[8] 佘 堃,沈 仟,周明天.背包问题在硬币抛掷协议上的研究[J].电子科技大学学报,2003,32(4):417-419.

[9] Heath D,Kinderlehrer D,Kowalczyk M.Discrete and continuous ratchets:from coin toss to molecular motor[J].Discrete and Continuous Dynamical Systems Series B,2002,2(2):153-168.

[10] Wagner D.Technical perspective:fairness and the coin flip[J].Communications of the ACM,2016,59(4):75.

[11] Zarkhin V,Sarwal M M.The coin toss of B cells in rejection and tolerance:danger versus defense[C]//Seminars in immunology.[s.l.]:Academic Press,2012:86-91.

[12] Larue D V.System and method for playing a game based on a coin toss:U.S.,8648710[P].2014-02-11.

[13] Ibsen-Jensen R, Miltersen P B. Solving simple stochastic games with few coin toss positions[C]//Algorithms-ESA 2012.[s.l.]:[s.n.],2012:636-647.

[14] Schneier B.应用密码学[M].吴世忠，祝世雄， 张文政,等,译.北京:机械工业出版社,2014.

Investigation on Tossing Coin Scheme

MA Li,DOU Jia-wei,WU Yan-mei

(College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China)

A coin toss is an important module of secure multi-party computation,and also has important application in real life.In network，the two sides of the coin toss are often not in the same place,but it still needs to be a fair decision.The fair coin toss is an important investigation direction.So both computer and network security,or everyday life,unfair issues with the coin toss need to be investigated and solved.Therefore,an unfair coin toss scheme has been designed with two-residual method and Legendre symbol after a fair coin toss scheme is constructed with one-way function and its effectiveness is verified,in which the probability for upward of the positive surface coin tossing is 0.25 while that of the opposite surface is 0.75.In network communication comparison and analysis on security and complexity of these two schemes have been conducted respectively.Analysis results show that the designs of two coin toss schemes in network communication are integratively merged with the combination of one-way function and coin tossing protocol and that the relevant protocols are simple and easy for implementation and convenient to be applied with vast prospective for actual application.

cryptography;secure multi-party computation;coin toss;discrete logarithm assumption

2016-05-26

2016-09-13

时间：2017-03-07

国家自然科学基金资助项目(61272435)；包头市科技局项目(2014S2004-2-1-15)

马 丽(1983-)，女，硕士研究生，研究方向为密码学与信息安全；窦家维，副教授，硕士生导师，研究方向为密码学与信息安全。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0921.054.html

TP31

A

1673-629X(2017)04-0117-03

10.3969/j.issn.1673-629X.2017.04.026