基于碳纳米管的纳机电系统的可控稳定振动
李健文,刘念华
(1.南昌大学材料科学与工程学院, 江西 南昌 330031; 2.南昌工程学院理学院,江西 南昌 330099;3.南昌大学高等研究院,江西 南昌 330031)
基于碳纳米管的纳机电系统的可控稳定振动
李健文1, 2,刘念华3
(1.南昌大学材料科学与工程学院, 江西 南昌 330031; 2.南昌工程学院理学院,江西 南昌 330099;3.南昌大学高等研究院,江西 南昌 330031)
采用数值方法研究了基于双壁碳纳米管的纳机电系统在周期性简谐驱动力作用下实现稳定振动的条件。确定了获得持久稳定的振动的系统和控制力参数。计算和分析了双壁碳纳米管的操作特性。结果表明,通过选择合适的驱动振幅和频率,能够实现双壁碳纳米管的持久稳定振动。该方法对于进一步研究基于碳纳米管的纳机电系统的设计有重要的参考价值。
纳机电系统; 纳米振子; 驱动频率; 稳定振动; 碳纳米管
1 Introduction
Carbon nanotubes (CNTs) are seamless quasi-one-dimensional structures with exceptional mechanical properties, such as remarkably high strength couple with extreme flexibility and toughness[1-3]. CNTs have received growing attention due to their potential applications as the basis for mechanically based motion control[4]. Low-friction, low-wear multiwall CNT bearings, realized first by Cummings and Zettl[5], aroused considerable interest. When the core is partially pulled out of the outer tube and then released, the inner tube can easily slide or rotate due to the intertube van der Waals (vdW) interaction. Such devices were reported to have extremely low friction—at least two orders of magnitude smaller than the vdW force[6]. These results led to much research work in exploring its possibility in making nano-oscillators based on nanoelectromechanical systems (NEMS). Zheng et al. confirmed the frequency to be in the gigahertz range[7]. Kolmogorov and Crespi analyzed the tribological properties of multiwalled carbon nanotubes (MWCNTs) and predicted that incommensurate tubes would have very small shear strengths[8].
The interaction between the tubes is dominated by physical vdW force, which makes the MWCNT oscillators can be studied by molecular dynamics simulations[9]and numerical calculations[6,10]. It was found that although a relatively smooth and low-frictional oscillator can be achieved by choosing an appropriate radius difference between inner and outer nanotubes (~0.34nm), friction-induced energy dissipation is still inevitable, resulting in damping oscillation[11]. The simulation showed that the time of the oscillation is within few nanoseconds. The short lifetime greatly limits its practical application because it brings difficulties for the energy supplement and signal detection. Thus how to sustain the CNT oscillatory motion in a controllable way over long periods of time remains a challenging problem. Different strategies have been proposed to study the oscillatory motion, e.g., by applying external magnetic fields with a conducting movable wall[12]and electrical fields in the case where ions are located inside the movable wall[13], by accelerating encapsulated charged elements located inside the inner tube[14], by thermal expansion of encapsulated gases which is enclosed between the walls of the nanotube[15], and by periodically applied thermal gradients[16], although it has been recognized that there are serious technological challenges[17].
It is known that, for a harmonic oscillator, the natural frequency has nothing to do with the initial displacement. However, the natural frequency of anharmonic oscillator is strongly dependent on the initial displacement. In the present work, a numerical method to maintain and control the stable motion of double walled carbon nanotubes (DWCNTs) is proposed. Periodical harmonic driving force is applied to the nano-oscillator with equal and unequal lengths of the core and shell. We determine the controllable operating conditions for the stable oscillation by the parameters of the oscillators and the driving force, and investigate the relation of the stable oscillation with the amplitude and the initial phase of the periodical driving force. This is an attempt to model the motion characteristics of a sliding core/shell DWCNT-type oscillator driven under periodical harmonic forces. Our aim is to explore the feasibility of the proposed method for controlling the stable motion of the oscillation system.
The rest of the paper is organized as follows. The model and the numerical methods in Section 2 are described briefly. In Section 3, we give the calculated results and demonstrate the possibility of controlling the stable oscillation of DWCNT systems. Conclusion is drawn in section 4.
2 Model and Method
We consider the DWCNT (4,4)@(9,9) with different lengths (5.99nm and 11.97nm) for the outer tubes and same length (5.99nm) for the inner tube as shown in Figure 1. Both ends of the inner and outer tubes are opened. The intertube distance is ~3.4, which coincides that between adjacent sheets of graphite. Since covalent bonds are much stiffer than vdW interaction, the DWNT can be modeled as a system of two rigid tubes moving coaxially. At the beginning of simulation, t=0, the inner tube is pulled out to a certain distancex(0) along their common axis, while the outer tube is fixed. After being released, the inner tube oscillates back and forth along the axial direction.
The analysis of the controlled properties of a DWCNT oscillator is performed using empirical interatomic potentials. The vdW interaction between the inner and outer tube atoms was used by the Lennard-Jones (LJ) pair potential which has the formUij=4ε[(σ/rij)12-(σ/rij)6],wheretheenergyandlengthparametersaretakenasε=2.964meV,andσ=3.407Å[18].ThepotentialprofilealongtheaxialdisplacementbetweenthecentersofthewallshasbeencalculatedandplottedinFig.1,whichisagreementwiththeresultscalculatedbyServantieandGaspard[18].TheLJapproachhasbeensuccessfullyusedformolecular-dynamicssimulationsofcarbonstructurestakingintoconsiderationitsrelativesimplicityandsatisfactoryresults[19-20].ItisindicatedthattheLJpotentialisveryeffectiveincalculatingtheoscillatoryfrequencyanddescribingthecharacteristicbehaviorofvariousCNToscillatorsystems[21-22].
Theoscillatorunderconsiderationisadampingoscillator.Inordertosustainthestableoscillationoftheoscillators,wehavetosupplytheenergytotheoscillator.Weassumethatthedissipatedenergyiscompensatedbyanexternalappliedperiodicalharmonicforce.Atarelativelylowoscillationamplitude,thedynamicfrictionforceisproportionaltotheoscillatorvelocity.Thus,theoscillatordynamicscanbedescribedbytheone-dimensionalequationsofmotion
dx/dt=y
(1)
μ(dy/dt)=-∂U/∂x-γy+Fmsin(ωt+φ)
(2)
whereμisthemassofthemovablecore,xis the displacement of the core with respect to the fixed shell,yis the relative velocity,Uis the LJ potential,Fmis the amplitude of driving force applied to the core with angular frequencyωand initial phaseφ, andγis the friction coefficient. Our model will impose constant values 6.1 amu/ps for the friction coefficient at a relatively low oscillation energy[18]. We suppose the initial velocity is always equal to zero. The eigenfrequency Ω of the oscillator is defined as the frequency of free oscillation without damping. Due to the anharmonic potential, Ω is dependent on the initial displacementx(0).

Fig.1 Configuration of the gigahertz oscillator based on the (4,4) @ (9,9) DWCNT and potential profile along the axial displacement with (a) equal inner and outer tube lengths 5.99nm, and (b) unequal lengths of 11.97nm for the outer tube and 5.99nm for the inner tube
In order to obtain stable oscillation, the states of the oscillator and the driving force must return to the original states after one periodT. The angular frequencyωof the driving force, therefore, has to be equal to integral multiple of the oscillator angular frequency Ω,ω=nΩ. Although these frequencies are only a small subset of total possible frequencies, the conditions are absolutely necessary. Limiting the solutions to this subset is not artificial. Outside this subset, the oscillatory system can not always fully restore in one period. Nevertheless this limitation is not essential for a harmonic potential because the natural frequency Ω is not dependent on the initial displacement.
If the initial conditions are proper, the energy that the periodical driving force afford is equal to the dissipation of oscillation energy due to the frictional force in the periodT, that is
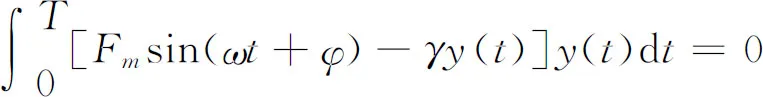
(3)
Thedisplacementattimetis dependent on many parameters, including the shape of the potential, the initial displacementx(0), the friction coefficient, and the frequency, amplitude and initial phase of the driving force, namelyx[t;Fm,ω,φ,γ,U(x),x(0)].Inordertosustainthestableoscillation,thedisplacementandthevelocitymustreturntotheinitialvaluesafteroneperiodT. This means
x[t=T;Fm,ω,φ,γ,U(x),x(0)]=x(0)
(4)
y[t=T;Fm,ω,φ,γ,U(x),x(0)]=y(0)
(5)
Itisverydifficulttodeterminetheconditionsconcerningmultipleparametersoperationforsustainedoscillator.Ifthefrequencyoftheharmonicdrivingforcesatisfiesω=nΩ, then the conditions of the stable oscillation are determined by the initial phase and the amplitude of the controlled force. Each equation of the combination gives a curve in theφ-Fmplane. The cross point of the two curves solves the combination of Eqs. (4) and (5). Here the Verlet velocity algorithm and steepest descent method were used to solve them.
3 Results and discussion
3.1 Unequal inner and outer tube lengths
In order to investigate the operating characteristics of the DWCNT oscillator controlled by the driving force, we firstly consider an oscillator of inner tube length 5.99nm and outer tube length 11.97nm. The frequency of free oscillation of the system depends on the initial extrusion of the inner tube for the anharmonic oscillator. For the initial displacementx(0)=5nm, it is found that the frequency of the oscillator in the case with the absence of the driving force and frictional force is Ω=0.1426. As demonstrated above, to sustain stable oscillation, the driving frequency must be equal to integral multiple of the oscillatory frequency once the inner tube is released from an initial displacement. For the driving frequencyω=3Ω andω=4Ω, the curves satisfying Eqs. (4) and (5) are shown in Fig.2. There are many solutions that satisfy Eq. (4) or (5), and one initial phaseφcorresponds to several amplitudesFm, same if vice versa. However, there is only several solutions within the range -2π~2π for the initial phaseφ. The cross points of the curves in theφ-Fmplane are (φ,Fm)=(-0.0227,0.0812)and(φ,Fm)=(0.3847,1.6540)forcase1andcase2,respectively.Asincreasingthedrivingfrequency,theamplitudeFmof the driving force needed to sustain the stable oscillation increases.
In theφ-Fmplane, we can measure the deviation that the displacement and velocity relative to the initial value after one time period with Δ=[x(T)-x(0)]2+[v(T)-v(0)]2.ThosepointsdropintotheregionofΔ<10-4,correspondingtotheshadedparts,canbetreatasstableoscillationapproximately.Sowecanconvenientlychoosedifferentinitialphasesandamplitudesofdrivingforcetosustainstableoscillation.

Fig.2 Sustainable oscillation amplitude and initial phase of unequal inner and outer tube lengths for (a) ω=3Ω and (b) ω=4Ω. The solid and dotted lines correspond to Eq. (4) and Eq. (5), respectively. A shaded part is shown in (a) to emphasize the possibility of obtaining more choices to sustain persistent oscillation
Theanalysishasbeenperformedwithreferencetothephasespace,examplesofwhichareshowninFig.3correspondingtocasesofFig.2.Weconsiderthatthetrajectoriesofinterestarethosethatformaclosedloopinoneoscillationcycle,asthesewillshowthedesirableaspectforanydrivenoscillatorsystem.ItisfoundthateverysolutionforthecombinationofEqs. (4)and(5)correspondstoaclosedloop.Thesimulationresultsindicatethatthephasediagramofeachoscillatorisnotastandardellipse,butasmoothloop.Consequentlytheoscillatorisanharmonicvibrationperiodically.Interestingly,theoscillationamplitudeisequalforthedrivingfrequencyω=3Ω and unequal for the driving frequencyω=4Ω. Furthermore, the phase trajectories are asymmetric. So the choice of the driving frequency has great influence on the behavior of the considered oscillator.
To understand the forces that contribute significantly to the oscillatory behavior, a typical result is shown in Fig.4 for case 1. It is indicated that the driving frequency is three times that of net force, velocity and displacement. Furthermore, we find similar results in the cases of both small and large initial displacements. As are explicitly plotted in Fig.3, the choice of the driving frequency has great influence on the behavior of the considered oscillator. Accordingly only if the driving frequency is equal to integral multiple of the oscillatory frequency and the initial phase and amplitude of the controlled force satisfy certain conditions which are determined by the combination of Eqs. (4) and (5), we can conveniently choose different initial displacements to sustain stable oscillation.

Fig.3 Resulting phase space trajectories corresponding to cases of Fig.2

Fig.4 (a) Driving force, (b) total force, (c) displacement, (d) velocity, and (e) total energy of the moving tube as a function of time for case 1. T and Tω are oscillation period and driving period, respectively
The driving force applied on the inner tube is periodical, the net force is not exactly zero after a driving periodTω, as shown in Fig.4. With regard to the same initial displacement and different driving forces, the displacement may be positive or negative and the oscillator may even move backward att=Tω. This state is the initial condition of next driving period, which has great effect on the following movement. Furthermore, probably the maximums of the positive and negative displacement also are unequal. Consequently the conditions to sustain the stable oscillation of DWCNT are very rigorous.
3.2 Equal inner and outer tube lengths
A similar analysis has been performed on a fixed shell and mobile core of equal lengths. We find that, for the initial displacementx(0)=-2nm of inner and outer shell lengthsL1=L2=5.99nm, the frequencies of the oscillator in the case with the absence of the driving force and frictional force is Ω=0.2493. Fig.5 depicts the solid lines and the dotted lines satisfying Eq. (4) and Eq. (5), respectively. The cross points of the curves in theφ-Fmplaneare(φ,Fm)=(2.9045,0.0292)and(φ,Fm)=(2.9891,4.1697)forcase3andcase4,respectively.

Fig.5 Sustainable oscillation amplitude and initial phase of equal inner and outer tube lengths for (a) ω=3Ω and (b)ω=4Ω

Fig.6 Resulting phase space trajectories corresponding to cases of Fig.5
ThecalculationresultsofthecontrolledstableoscillationsarepresentedinFig.6forequallengthDWCNToscillators.Comparingwiththecasesofunequallength,weobservedsimilarphenomena.Althoughtheoscillationbehaviorsaremorecomplicated,wecanrealizesustainedoscillationwithmanychoices.
4 Conclusion
In summary, we have performed numerical computations to understand the oscillatory characteristics and the stability of DWCNT-based oscillators driven by periodical harmonic force. We demonstrate that the use of proper driving force can be an effective approach to control and tune CNT-based oscillators. The parameters and characteristics corresponding to the controllable operating conditions for the stable oscillators are determined. If we choose the amplitude and the initial phase of the periodical harmonic driving force satisfying the conditions of the combination of Eqs. (4) and (5), we can realize stable oscillation of the DWCNT-type oscillator.
Reference
[1] S. Iijima, T. Ichihashi. Single-shell Carbon Nanotubes of 1-nm Diameter [J]. Nature (London), 1993, 363: 603~605.
[2] H. J. Shen. Transverse and Axial Stiffness of Carbon-tube Nanosprings [J]. J. Mater Sci. Eng, 2007, 25(6): 814~817.
[3] H. J. Shen, X. C. Mu. FE Analyses of Tensile “Y”-shaped, Bamboo-shaped and Straight Carbon Nanotubes [J]. J. Mater Sci. Eng., 2005, 23(3): 321~324.
[4] E. H. Cook, M. J. Buehler, Z. S. Spakovszky. Mechanism of Friction in Rotating Carbon Nanotube Bearings [J]. J. Mech. Phys. Solids, 2013, 61(2): 652~673.
[5] J. Cummings, A. Zettl. Low-friction Nanoscale Linear Bearing Realized from Multiwall Carbon Nanotubes [J]. Science, 2000, 289(5479): 602~604.
[6] J. L. Rivera, C. McCabe, P. T. Cummings. Oscillatory Behavior of Double-walled Nanotubes under Extension: a Simple Nanoscale Damped Sping [J]. Nano Lett., 2003, 3: 1001~1005.
[7] Q. Zheng, Q. Jiang. Multiwalled Carbon Nanotubes as Gigahertz Oscillators [J]. Phys. Rev. Lett., 2002, 88(4): 045503~045505.
[8] A. N. Kolmogorov, V. H. Crespi. Smoothest Bearings: Interlayer Sliding in Multiwalled Carbon Nanotubes [J]. Phys. Rev. Lett., 2000, 85(22): 4727~4730.
[9] M. V. D. Prasad, B. Bhattacharya. Molecular Dynamics Simulations of Carbon Nanotube-based Oscillators having Topological Defects [J]. Int. J. Nanosci., 2011, 10(1): 1~5.
[10] A. Neild, T. W. Ng, Q. Zheng. Controlled Driven Oscillations of Double-walled Carbon Nanotubes [J]. EPL, 2009, 87: 16002~16006.
[11] J. L. Rivera, C. McCabe, P. T. Cummings. The Oscillatory Damped Behaviour of Incommensurate Double-walled Carbon Nanotubes [J]. Nanotechnolog, 2005, 16: 186~198.
[12] S. B. Legoas, V. R. Coluci, S. F. Braga, P. Z. Coura, S. O. Dantas, D. S. Galvao. Gigahertz Nanomechanical Oscillators Based on Carbon Nanotubes [J]. Nanotechnology, 2004, 15: S184~S189.
[13] J. W. Kang, H. J. Hwang. Gigahertz actuator of Multiwall Carbon Nanotube Encapsulating Metallic Ions: Molecular Dynamics Simulations [J]. J. Appl. Phys., 2004, 96(7): 3900~3905.
[14] O. V. Ershova, Y. E. Lozovik, A. M. Popov, O. N. Bubel, E. F. Kislyakov, N. A. Poklonskii, I. V. Lebedeva. Control of the Motion of Nanoelectromechanical Systems Based on Carbon Nanotubes by Electric Fields [J]. J. Exp. Theor. Phys., 2008, 107(4): 653~661.
[15] J. W. Kang, K. O. Song, O. K. Kwon, H. J. Hwang. Carbon Nanotube Oscillator Operated by Thermal Expansion of Encapsulated Gases [J]. Nanotechnology, 2005, 16: 2670~2676.
[16] V. R. Coluci, V. S. Timóteo, D. S. Galvão. Thermophoretically driven carbon Nanotube Oscillators [J]. Appl. Phys. Lett., 2009, 95: 253103~253105.
[17] L. Forró. Beyond Gedanken Experiments [J]. Science, 2000, 289(5479): 560~561.
[18] J. Servantie, P. Gaspard. Translational Dynamics and Friction in Double-walled Carbon Nanotubes [J]. Phys. Rev. B, 2006, 73: 125428~125440.
[19] J. P. Lu, W. Yang. Shape of Large Single- and Multiple-shell Fullerenes [J]. Phys. Rev. B., 1994, 49: 11421~11424.
[20] C. H. Sun, G. Q. Lu, M. H. Cheng. Single-particle distribution functions in Nanoscale particles at finite temperature: some rigorous results [J]. Phys. Rev. B, 2006, 73(19): 195414~195418.
[21] C. C. Ma, Y. Zhao, C. Y. Yam, G. Chen, Q. Jiang. A Tribological study of Double-walled and Triple-walled Carbon Nanotube Oscillators [J]. Nanotechnology, 2005, 16: 1253~1264.
[22] T. A. Hilder, J. M. Hill. Oscillating Carbon Nanotori along Carbon Nanotubes [J]. Phys. Rev. B, 2007, 75: 125415~125422.
LIU Nianhuan, E-mail: nhliu@ncu.edu.cn.
Controlled Stable Oscillations of Carbon Nanotube-based NEMS
LI Jianwen1,2, LIU Nianhua3
(1.School of Materials Science and Engineering, Nanchang University, Nanchang 330031, China;2.School of Science, Nanchang Institute of Technology, Nanchang 330099, China; 3.Institute for Advanced Study, Nanchang University, Nanchang 330031, China)
A numerical method was used to investigate the conditions to sustain the stable motion of nanoelectromechanical systems (NEMS) based on carbon nanotubes under periodical harmonic driving force. We determined the parameters of the system and control force which allow obtaining the sustained stable oscillation at a constant frequency. The operating characteristics of the double-walled carbon nanotube oscillators were calculated and analyzed. It is shown that the sustained stable motion of the oscillators can be realized by properly choosing the amplitude and the initial phase of the periodical harmonic driving force. The method reported here is believed to have important implications in carbon nanotube-based NEMS design.
NEMS; nano-oscillator; driving frequency; stable oscillation; carbon nanotube
TB34 Document code:A
1673-2812(2017)02-0203-06
Foundation item:Supported by the National Basic Research Program of China (973 Program) (2013CB934200), the Key Program of the National Natural Science Foundation of China (10832005) and the National Natural Science Foundation of China (11264030)
10.14136/j.cnki.issn 1673-2812.2017.02.007
Received date:2015-10-20;Modified date:2016-04-11
Biography:LI Jianwen, male, Ph.D. candidate, research direction: nanosurface science and engineering. E-mail: ljw624@126.com.

