数学课堂“尾声”的有效设计

范炳南

课堂尾声，指的是数学课堂的后十分钟，这是对当堂学习知识有针对性的消化、巩固，对于数学课堂学习中存在问题的反馈时间。合理设计这块内容，不仅有利于学生知识输入，还有利于学生知识输出，促进学生对自身所学知识进行分析归纳，查漏补缺，提高自身知识的综合运用能力，增强学习实效性，使学生学习能力的培养得到有效落实。

基于此，笔者一直关注着基于“问题反馈”的数学课堂后十分钟检测设计与操作的研究，尝试着突破过去的学习模式，融入新理念，凸显过程与方法，结合所任教班级的现状，开展数学课堂中后十分钟检测，从中把握学生的认知结构，预测学生将会碰到的思维障碍及形成障碍的原因，调控、掌握事先预测到的学生可能会出现的问题，进一步优化数学课堂教学，从中找出有规律的操作程序，然后再把这种操作程序用课堂教学进行验证。

一、研究的必要性

自新课改以来，教师的角色变了，教与学的方式变了，数学日常教研活动所关注的重点也发生了改变。关注重心从教师的“教”为中心转移到学生的“学”为任务，课堂教学从学生全面发展的需要出发，尊重学生的人格和个性发展，注重学生发展性目标的形成。但在日常数学教学中，从重视练习到强化练习，由多练到“海”练，其集中表现：一是课内教师拼命地讲，课外学生拼命地练；二是只追求练习数量而不讲求质量和效果。很多时候感觉到一节数学课下来，教师对学生学习的达成情况不明，对学生存在的问题不能及时了解，不能及时有效地对学习进行补救与调控，最终导致学生练得可怜，教师批得辛苦，而实际效果却不尽如人意。

二、实践策略

课堂后十分钟的检测设计和操作要把握适切性、简约性、诱导性原则，使学生原认知结构中有关内容同所要学习内容产生链接，将结构性的数学知识与学生的生活实际有机整合，引发学生思考、促进学生发展。数学课的课型分为新课、练习课和复习课，根据三种课型归纳出可操作的课堂检测有两种类型：巩固型检测和发展型检测。

1.巩固型检测的设计与操作。

巩固型检测是新课教学中巩固新知的重要途径和方法之一，是教师获得反馈信息的桥梁，是师生交流信息的窗口。

（1）矫正型小检测。

矫正型检测就是依据这样的理念，以学生的普遍错误为素材，以纠正错误、强化方法、形成技巧为目的，通过题组比较、方法指导等手段帮助学生分辨相似问题的异同，使他们能正确地掌握解题的方法与技巧的小测验。

案例1：在《平行四边形面积计算》学习中的检测设计：

出示课件：屏幕上是一个平行四边形，你有什么办法来求出它的面积。（学生在作业纸上独立完成）教师巡视，请两位同学到黑板上板演。

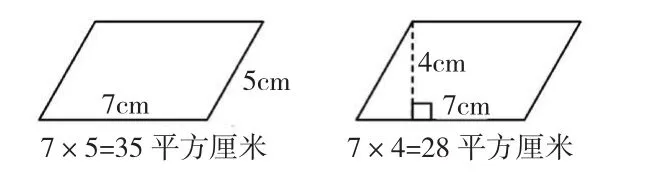
师：谁来说说看，你们支持哪种做法，为什么？

生1：我觉得第一种对。因为平行四边形有易变性，我们把平行四边形拉成一个长方形，平行四边形的底就是长方形的长，平行四边形的邻边就是长方形的宽。因为长方形的面积=长×宽，所以平行四边形的面积=底×邻边。

生2：老师，我觉得第二种对，如果把平行四边形拉成一个长方形以后，面积变了，面积不相等，平行四边形的面积就不等于底×邻边。

师：其他同学，你认为把一个平行四边形拉成一个长方形以后，面积有没有发生变化？

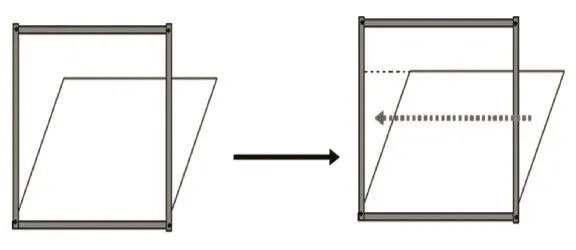
生3：面积发生了变化，如果把平行四边形露在外面的那个三角形剪下来（如上图），拼到里面，原来平行四边形的面积就等于下面这个小长方形的面积，而上面这个小长方形就是多出来的面积，所以，我认为，把平行四边形拉成长方形以后，面积变大了。

矫正型检测的过程其实是学生思维斟酌过程，更是一个学生自主学习、自主发展的过程。学生自己通过反思、判定去发现问题、解决问题，充分体现了学生的主体意识；同时这种小检测能有的放矢地帮助学生改正错误，它量少质高，符合学生在课堂中实际的学习需求；同时又能在最大限度内减轻学生课业负担，优化课堂效益。

（2）强化型小检测。

强化型小检测是指在数学新课中，以数学概念的正确理解、数学方法的熟练运用、数学技巧的准确把握为目的而进行的小检测。此类检测重点是考查学生对基本概念、方法与技巧的掌握程度，使教师能更准确、更真实地把握学生的学情，加强对基础知识的理解和应用，加强数学知识点和板块内容间的训练，加强对基本技能的训练，掌握知识之间的内在联系，理清知识结构，形成知识网络，在应用中理解其本质，实现由知识到能力的跨越。

案例2：在教学《商不变的性质》学习中的检测设计：

创设情境

师：森林里马上要举行聚餐活动，所以派了3个小动物去买水果，可是它们也带来了一个问题请教同学们。

出示幻灯（小鸡用90元买了30元/千克的苹果，小猴用45元买了15元/千克的香蕉，小羊用180元买60元/千克的草莓。谁买的水果最多？）

师：看懂了吗？请你来说一说，你怎么知道的？

生：我猜他们买得一样多，可以算一算：

90÷30=3（千克）

45÷15=3（千克）

180÷60=3（千克）

探索奥秘

师：你还能说出哪些商是3的除法算式？

有效备选：30÷10、9÷3……

师：请观察上面这些算式，你有什么发现？

设想1：

师：被除数和除数到底是怎么变的？

生：商没有变，被除数和除数变了。

设想2：

师：到底这些被除数和除数之间还藏着什么小秘密呢？

生：被除数×2，除数×2。

学习要求：

①仔细观察算式，思考被除数和除数是怎么变的；

②把你的发现在四人小组里交流。

指导：注意学生的用语，提醒“同时”。

小组汇报：

生：我发现被除数和除数同时×2，商不变。

生：我发现被除数和除数同时÷2，商不变。

生：被除数和除数同时乘或同时除以同一个数，商不变。

师：刚才我们观察的都是商是3的算式，如果两个算式的商不是3，而是别的数字，你猜猜，被除数和除数之间还存在这样的关系吗？

生：不一定。

生：试一试，验证一下。

生：写两个商是一样的除法算式，然后看看被除数和除数有没有这样的关系。

（学生猜测、验证）

师：利用今天发现的规律试一试。

90÷15=（90 ÷3）÷（15÷3）

300÷25=（300×2）÷（25○□）

480÷12=（480○□）÷（12○□）

师：第三题，到底有多少个答案？怎么来判断他的答案？究竟一共有几种填法？

师：（追问）是不是所有的数都可以？

学生猜测：除不尽不行，比除数小不行。

师：举例，如果都写5，像这样的算式虽然我们现在的知识还不能算，但符合今天的结论。

师：480÷12=（480×0）÷（12×0）。看看这个算式行不行？你对这个结论还有什么要补充的？

结论：被除数和除数同时乘或同时除以同一个数（0除外)，商不变。

本案例中，笔者给予三个规律相同的同类型算式，目的是便于学生发现规律，然后让学生自己举出大量例子，用不完全归纳法归纳出“商不变的性质”。

2.发展型检测的设计与操作。

新课改的基本理念中明确提出教育要面向全体学生的全面发展，关注个体差异，满足不同学生的学习需求，使每个学生都能得到充分的发展。因而在数学练习课中设计多样化的发展性检测，让学生针对自身情况进行选择性或实践性的小检测，不仅有利于学生对所学过知识的应用、掌握和理解，而且还能让学生体会数学与生活的深刻联系。

选择型小检测。

选择型小检测是指教师根据学生已有知识、掌握程度的不同，为学生提供不同层次的检测，允许学生根据自己的能力来选择的课堂小检测。

案例3：《长方形和正方形的面积》课堂中的菜单式作业设计：

（1）计算下面长方形、正方形的面积（1☆）

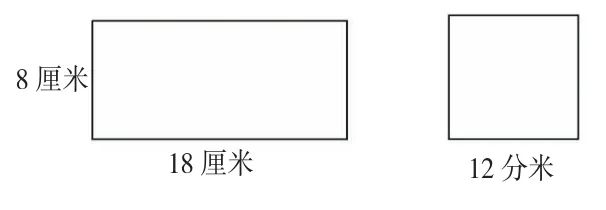
（2）计算出下面每个图形的面积和周长。（1☆）

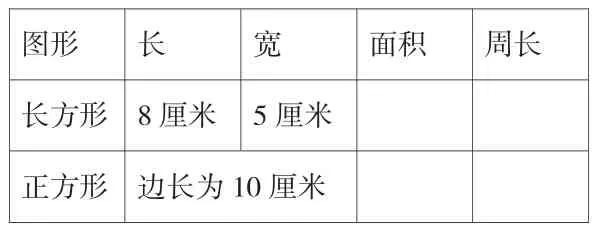
图形 长 宽 面积 周长长方形 8厘米 5厘米正方形 边长为10厘米

（3）一个长方形花圃，长40米，宽 25米。（2☆）

①这个花圃的占地面积是多少平方米？

②在这个花圃的周围围一圈栏杆，栏杆的长度是多少米？

4.你能算出阴影部分的面积吗？（3☆）

针对不同层次的学生，在选择型检测中，有意识地编拟多个星级的题目，层层加深，使学生有了自主选择权，给了学生更大的展示空间。学困生可以只选择1☆或者2☆的题目，中等生在完成基础题的同时可以去尝试完成3☆题，优等生则可以选2☆和3☆题目完成。在检测中，学生也表现出了很高的积极性和创造性，使不同层次的学生都尝试到成功的喜悦，从而产生积极向上的学习情绪，在愉快中达到自己的学习目标，感受努力付出换来成功的喜悦。

分层型小检测。

由于学生接受能力和思维水平的差异，在学习中常有优等生吃不饱，后进生不明了的现象。这时，教师就要根据学生的年龄特征、认知能力，设置分层检测，改变原有的“一刀切”的评价方法入手，以数学分层检测卡为载体，在课堂教学中，可以在数学分层检测卡中设置二至三层检测题，每层都编写了一至三道题。第一层主要是针对学生当堂所学新内容的掌握情况的检测，第二或三层主要侧重于思维和能力的检测，这样只要认真学了当堂课，学生就能得到好成绩。这也是我们在研究课堂后十分钟检测设计与操作研究中最常用的一种，也是用得最多的一种方法。

案例4：《长方体的体积计算》课堂中的分层式作业设计：

一类：

分层检测卡A层：已知一个长方体的长为18厘米，宽和高为13厘米，求其体积是多少？

二类：

分层检测卡B层：一辆货车运来4立方米的沙子，把这些沙子倒在一个长5米，宽2米的沙坑，问沙坑厚多少？

三类：

分层检测卡C层：一个长5分米，宽3分米，高6分米的长方体容器内装入3分米高的水，现在把这个容器竖立起来，问现在水的高度是多少？

运用数学分层检测卡，让不同层次的学生深入、比较、探究、弄清长方体体积综合应用的有关解决问题的方法，让不同层次的学生在基础和能力上各得其所，这样的设计既保证了尖子生的培养，也可避免学习成绩中等偏下的学生看到稍难点的题目就束手无策的现象。