前缘缝翼尾缘喷流对多段翼流场的影响研究

杨 茵, 陈迎春, 李 栋,*

(1. 西北工业大学 航空学院流体系, 陕西 西安 710072; 2. 中国商用飞机有限公司 上海飞机设计研究院, 上海 201102)



前缘缝翼尾缘喷流对多段翼流场的影响研究

杨 茵1, 陈迎春2, 李 栋1,*

(1. 西北工业大学 航空学院流体系, 陕西 西安 710072; 2. 中国商用飞机有限公司 上海飞机设计研究院, 上海 201102)

为了研究前缘缝翼尾缘剪切层对多段翼气动性能的影响，通过在前缘缝翼尾缘添加喷流的方式来改变缝翼尾缘处的剪切层。选取不同的喷流流量和流速等参数，利用CFD手段研究了喷流对缝道的速度分布以及多段翼各个翼面气动力的影响。多段翼二维非定常流场由有限体积法求解的二维非定常雷诺平均Navier-Stokes方程得到。分析结果得到：前缘缝翼尾缘添加喷流后对多段翼各个翼面压力分布和最大升力系数均有较大影响,其中，主翼最大升力系数、总的最大升力系数、前缘缝翼和后缘襟翼升力系数随着喷流动量系数增加而增加。

前缘缝翼；多段翼；喷流；最大升力系数；缝道

0 引 言

飞机在起飞和降落时，需要尽量降低飞行速度和缩短滑跑距离，因此需要具有较大的升力系数。但飞机在正常的着陆迎角下，由于飞行速度较低，需要高升力系数来提供升力，因此需要增加增升装置来提高升力。常见增升方式包含机械增升和动力增升，现在除了这两种传统的增升方式，又兴起了很多新的主动控制技术，其中包括：等离子体技术[1-2]、涡流发生器[3-6]、零质量射流[7-10]、自激励运动襟翼[11-12]和Zhu’s襟翼[13-15]等等。

机械式增升通过设计前缘襟翼或前缘缝翼、后缘襟翼和缝道来实现增升目的，而动力增升则是通过向襟翼表面弦向吹气和展向吹气来实现增升。动力增升主要通过向边界层吹气或者吸气来提高边界层的动量，从而克服逆压梯度，避免分离，进而大幅提升机翼的气动性能[16]。当机械式增升装置不能满足飞行性能要求时，动力增升方式能提供飞机所需的气动力。John[17]系统地研究了向襟翼吹气和吸气后襟翼气动力的变化。John认为在相同襟翼弦长的条件下，吹气襟翼能够最大程度地提升机翼的气动性能。Ibraheem[18]等在二维翼型和三维机翼尾缘处加入吸气、吹气装置，通过数值计算证明了吹气、吸气装置能够使升力系数有明显增加。国内的一些科研成果[19]也证实，吹气襟翼明显优于吸气襟翼，除了吹气和吸气襟翼外, 其他襟翼的增升能力均低于95%, 而吹气襟翼增升可达140%。因此，选择合适的动力增升装置能够显著提升机翼的气动性能。

作为机械增升装置的一部分，前缘缝翼对升力增加和失速延迟都有着重要的影响。而动力增升也能实现增升和延迟失速的效果，鉴于二者对多段翼增升和失速的影响，尝试将二者结合起来，以期提高多段翼的气动性能。不同于前人改变前缘缝翼下表面、改变缝道参数或者在主翼边界层添加吸取或者吹气装置，本文用在前缘缝翼尾缘添加喷流的方式将动力增升方式与机械增升装置结合起来，突破模型构型的限制，在不改变机械增升装置结构的前提下，利用动力增升改变多段翼流场，提升多段翼气动性能。

本文采用数值模拟的方法，研究在改变前缘缝翼尾缘后添加喷流，以此改变前缘缝翼尾缘尾流。经数值计算发现，多段翼各个翼面的升力及压力分布均随喷流动量系数的改变而发生的变化。其中，多段翼的升力会随着喷流动量系数的增加而增加。通过本文数值结果，发现了多段翼的增升的一个新思路和研究方向，即：通过改变前缘缝翼尾缘尾流提升多段翼升力。

1 数值模型

本文采用的原始模型为30P30N[20]，是McDonnell Douglas公司的一种襟翼模型，主要工作状态为迎角19°附近的着陆构型。模型中前缘缝翼与后缘襟翼的偏角均为30°，具体如图1所示。

为增加前缘缝翼尾缘喷流的截面积，分别切去前缘缝翼尾缘处10%、20%和25%缝翼弦长，得到了三组构型：Model.1、Model.2和Model.3，并且定义原始模型为Model.p，示意图见图2。鉴于模型其他部分一致，因此图2只显示了各个模型的前缘缝翼。

图1 模型30P30N Fig.1 Model 30P30N

图2 计算模型的前缘缝翼示意图Fig.2 Slats sketch map of all calculation models

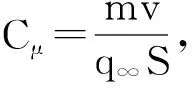
2 数值验证

2.1 30P30N数值验证

本文的数值计算采用有限体积法求解Navier-Stokes方程，其中对流项格式采用二阶迎风格式，扩散项格式采用二阶中心差分格式。湍流模型选择剪切应力输运(SST)k-ω模型。计算条件为：Ma=0.2，Re=9.0×106。数值计算采用C-H型结构网格，网格数约83 000，网格如图3所示。

图3 模型30P30N的结构网格Fig.3 Structure grid of model 30P30N

为了保证数值计算的准确性，将计算结果与文献[21]中的实验结果比较，分别对比了不同迎角下前缘缝翼、主翼以及后缘襟翼的升力系数及压力分布。数值计算与实验升力系数比较如图4，迎角α=16°时各个翼面压力分布如图5。通过数值计算与实验结果的比较可以看出，数值计算的结果与实验结果在迎角较小时比较吻合，在失速迎角附近主翼升力系数与总升力系数的差别比较大，对于总升力的最大升力系数来说，计算值相对实验值的误差约为3%。

图4 升力系数的计算与实验结果对比Fig.4 Comparison of lift coefficients between calculation and experiment results

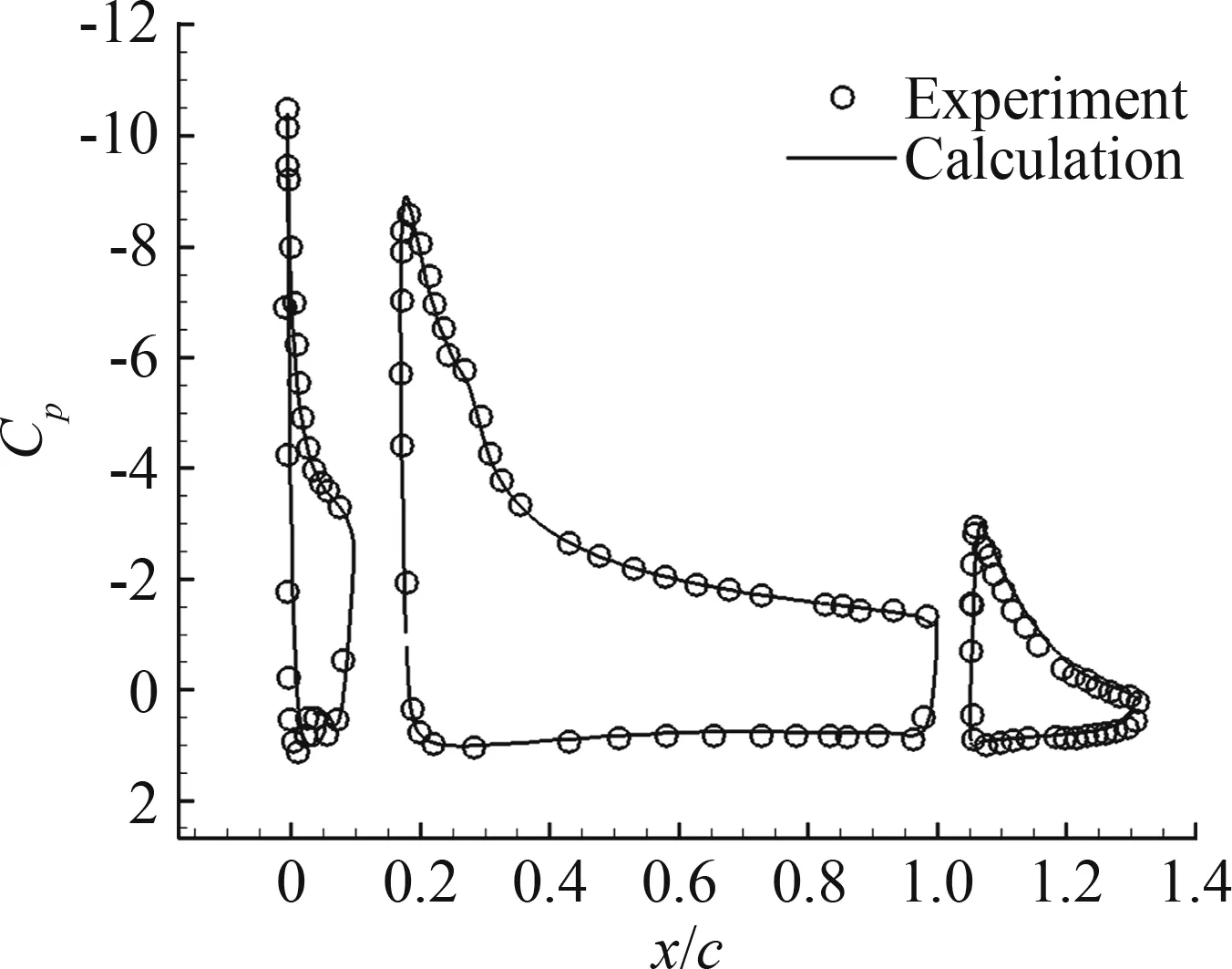
图5 压力系数的计算与实验结果对比(α=16°)Fig.5 Comparison of pressure coefficients between calculation and experiment results(α=16°)

2.2 喷流数值验证

张老师开始反思教育价值观和外语教育的根本目标。在参加学生座谈会的记录里，“大学英语学习终极目标”、“长远发展”等字眼，反映她把英语教学和培养人的综合素质联系起来，逐渐形成“教书育人”的教育信念。

为了验证本文选择的数值方法对喷流的模拟是准确可靠的，本文对文献[22]中的模型做了数值验证。模型如图6所示，喷流数值验证模型为椭圆翼型，弦长c为0.102m，厚度为0.2c，喷口高度为0.0015c，前后缘半径为0.04c，前后两个喷口分别位于3.7%c和96.3%c处。

数值计算选择O-H型结构网格，网格量为4.5万，网格如图7所示。数值计算方法与多段翼数值验证方法相同，均采用有限体积法求解Navier-Stokes方程。喷流实验结果是在雷诺数Re=2.0×105、迎角为0°、只有后缘有喷流时的水洞实验结果。本文选取了三个喷流动量系数0.032 46、0.781 188和0.1进行数值模拟，数值结果与实验结果对比如图8所示。对比实验结果发现，数值结果与实验结果吻合良好，因此可以认为，本文选择的数值计算方法对喷流的计算是可靠的，数值结果可信。

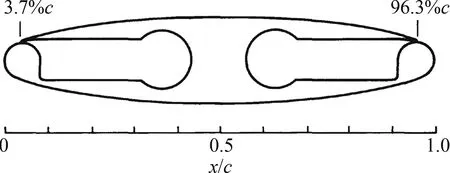
图6 计算模型示意图[22]Fig.6 Slats sketch map of calculation model[22]

图7 模型网格Fig.7 Structure grid of model

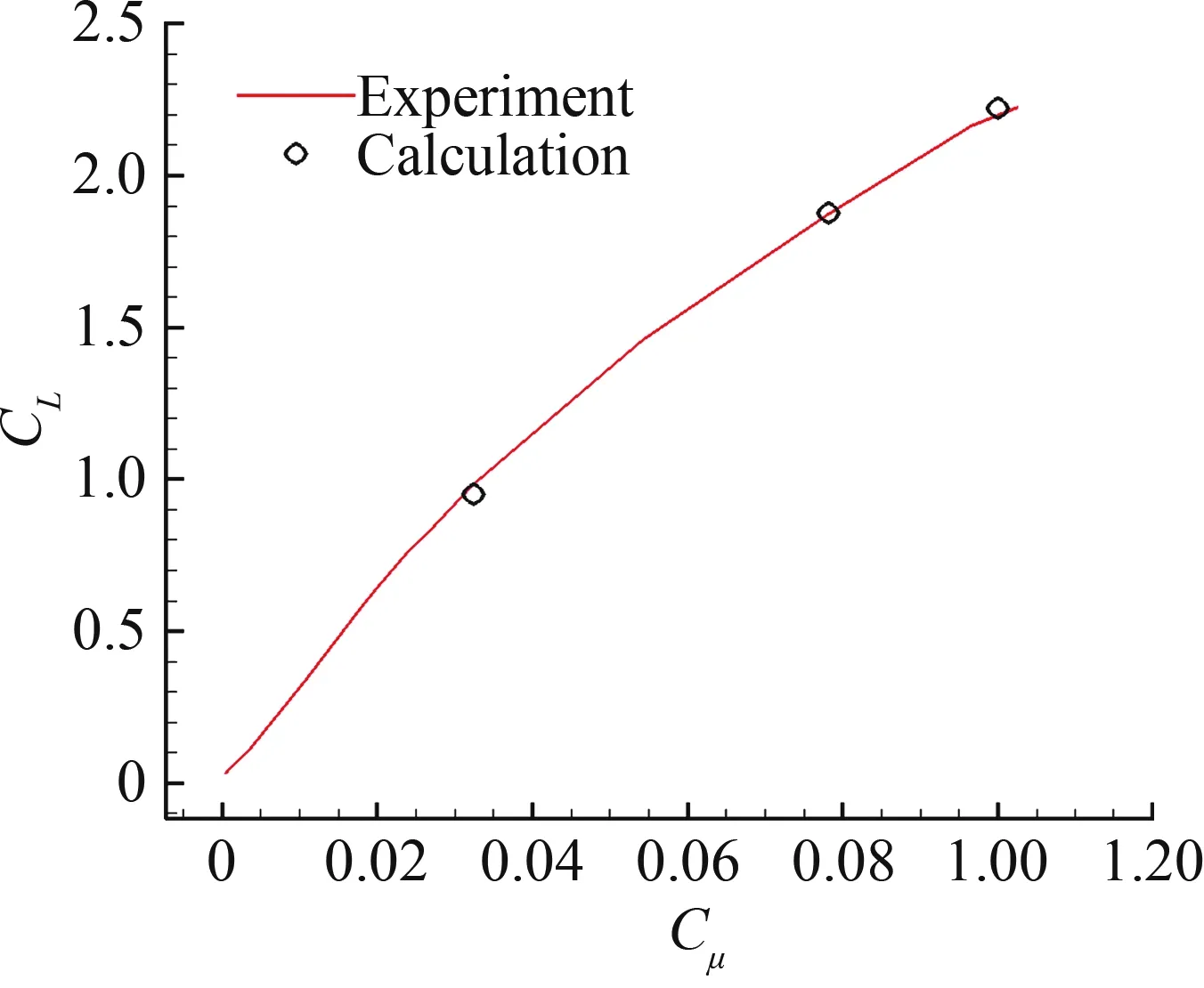
图8 升力系数的计算与实验结果对比Fig.8 Comparison of lift coefficients between calculation and experiment results

3 计算结果及分析

3.1 不同喷流速度对多段翼气动力的影响分析

在分析不同喷流速度带来的影响时，选同一模型Model.3。本节以及后续计算状态均为Ma=0.2，Re=9.0×106。图9为Model.p在迎角0°时的速度云图，主翼上表面前缘附近最大速度约为160m/s，马赫数约为0.47。因此，在选择前缘缝翼尾缘喷流速度时，选择的最小喷流马赫数与0.47相近，为0.5。为了分析不同喷流马赫数带来的影响，在前缘缝翼尾缘分别添加不同的喷流速度，添加的不同喷流马赫数分别为0.5、0.8和1.0，对应的喷流动量系数分别为0.070 9、0.181 5和0.283 6。

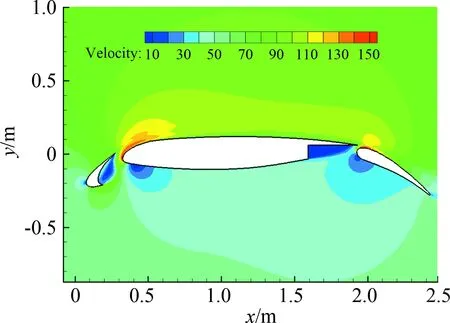
图9 Model.p的速度云图Fig.9 Velocity contour of Model.p

图10 (a～d)分别为Model.3前缘缝翼尾缘在不同速度的喷流下后缘襟翼、前缘缝翼、主翼以及总的升力曲线。由图10可以看出，各个翼面升力系数及总升力系数均随着喷流动量系数的增加而增加。喷流动量系数的增加增大了最大升力系数，但对失速迎角影响很小。

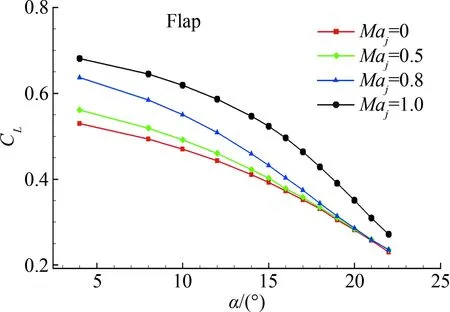
(a) 后缘襟翼升力系数

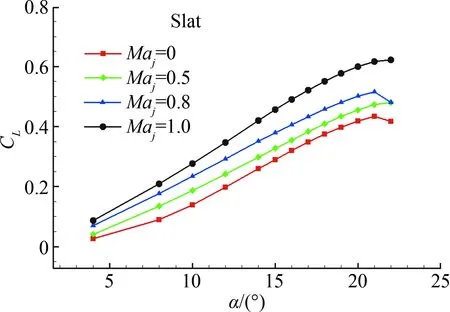
(b) 前缘缝翼升力系数

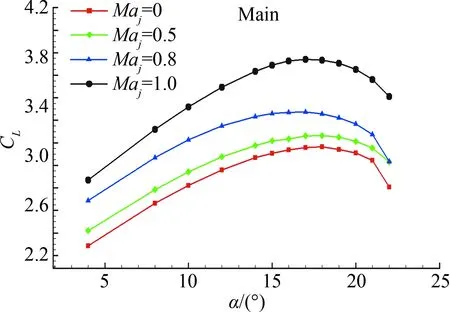
(c) 主翼升力系数

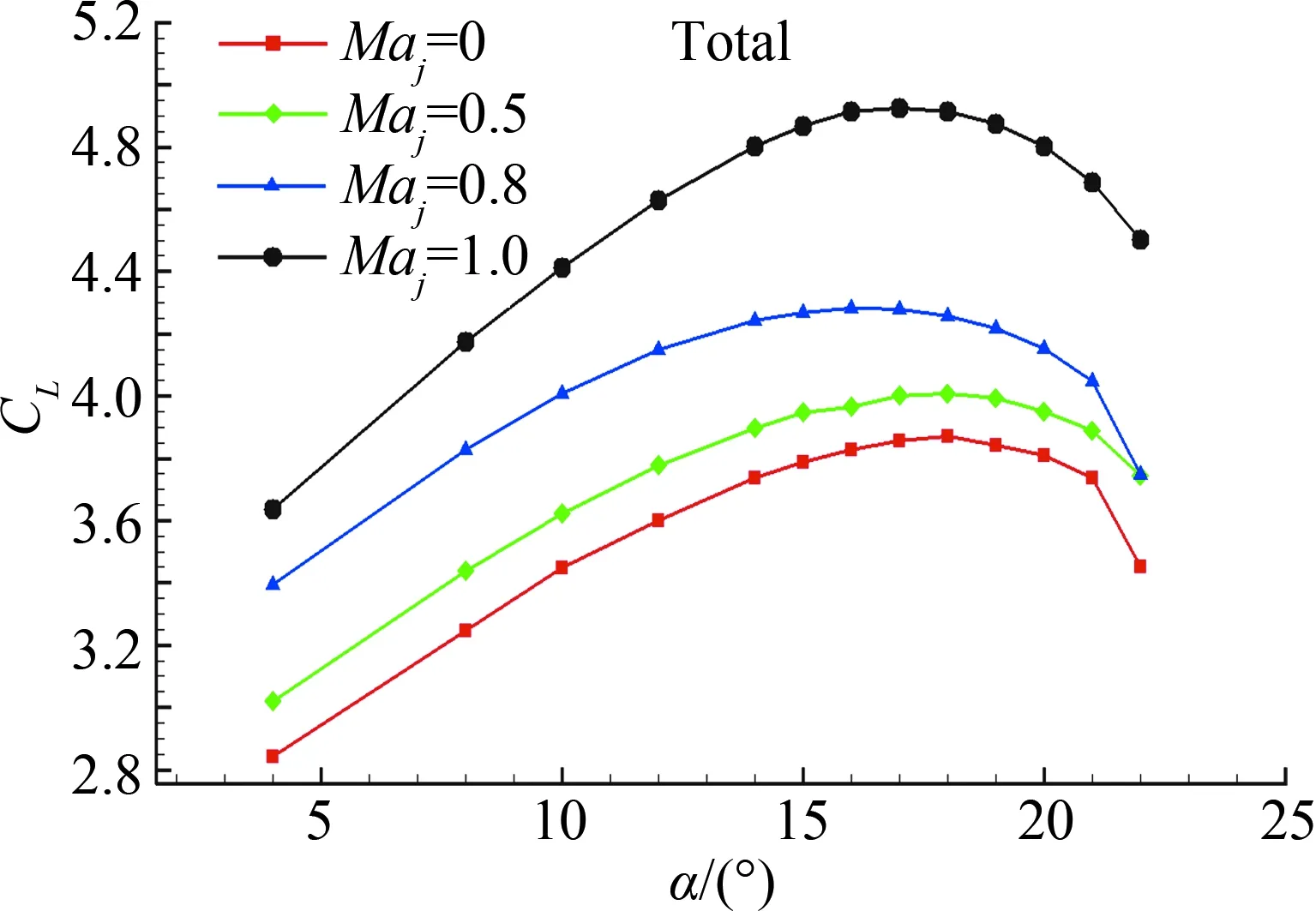
(d) 总升力系数

喷流速度增加后，各个翼面升力均有增加，对于后缘襟翼来说，喷流流速增加，会加快后缘襟翼上表面的流速，因而提高后缘襟翼前缘吸力峰峰值，提高了后缘襟翼的升力，见图11(a)。前缘缝翼增升是因为前缘缝翼尾缘喷流速度增加，由于剪切作用加速了前缘缝翼上下表面的流速，因而提高上下表面的压力水平，如图11(b)所示。主翼升力增加的主要原因是由于喷流速度增加，喷流与前缘缝翼尾缘缝道流动的剪切作用，加速了主翼上表面的流体流速，进而提高了主翼上表面的压力水平，如图11(c)所示。总之，提升前缘缝翼尾缘喷流的速度，增大动量系数能够提升多段翼各个翼面的升力水平。

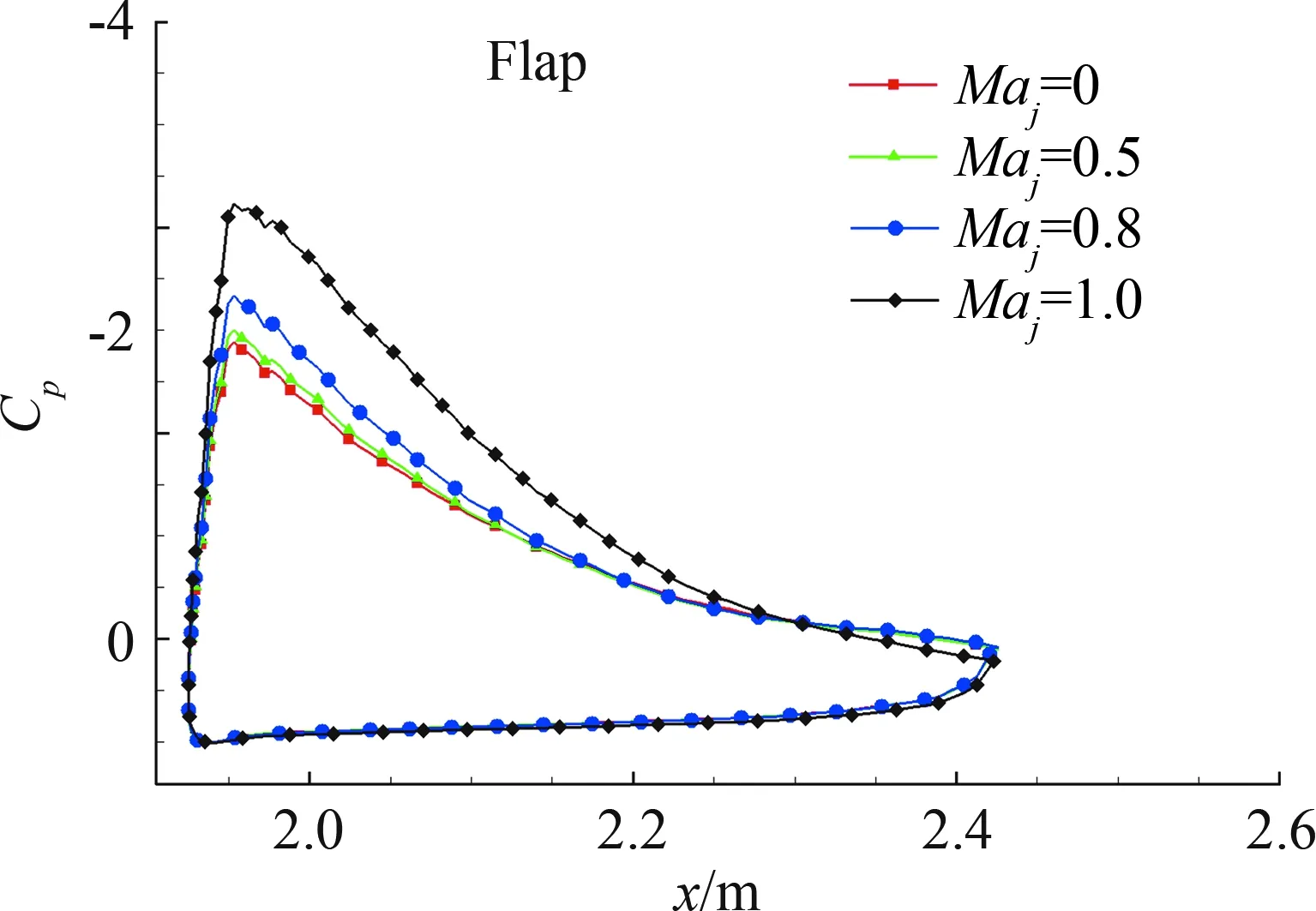
(a) 后缘襟翼压力系数

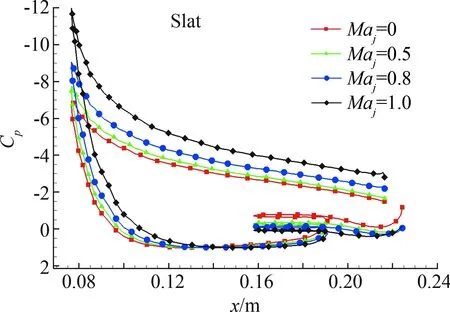
(b) 前缘缝翼压力系数

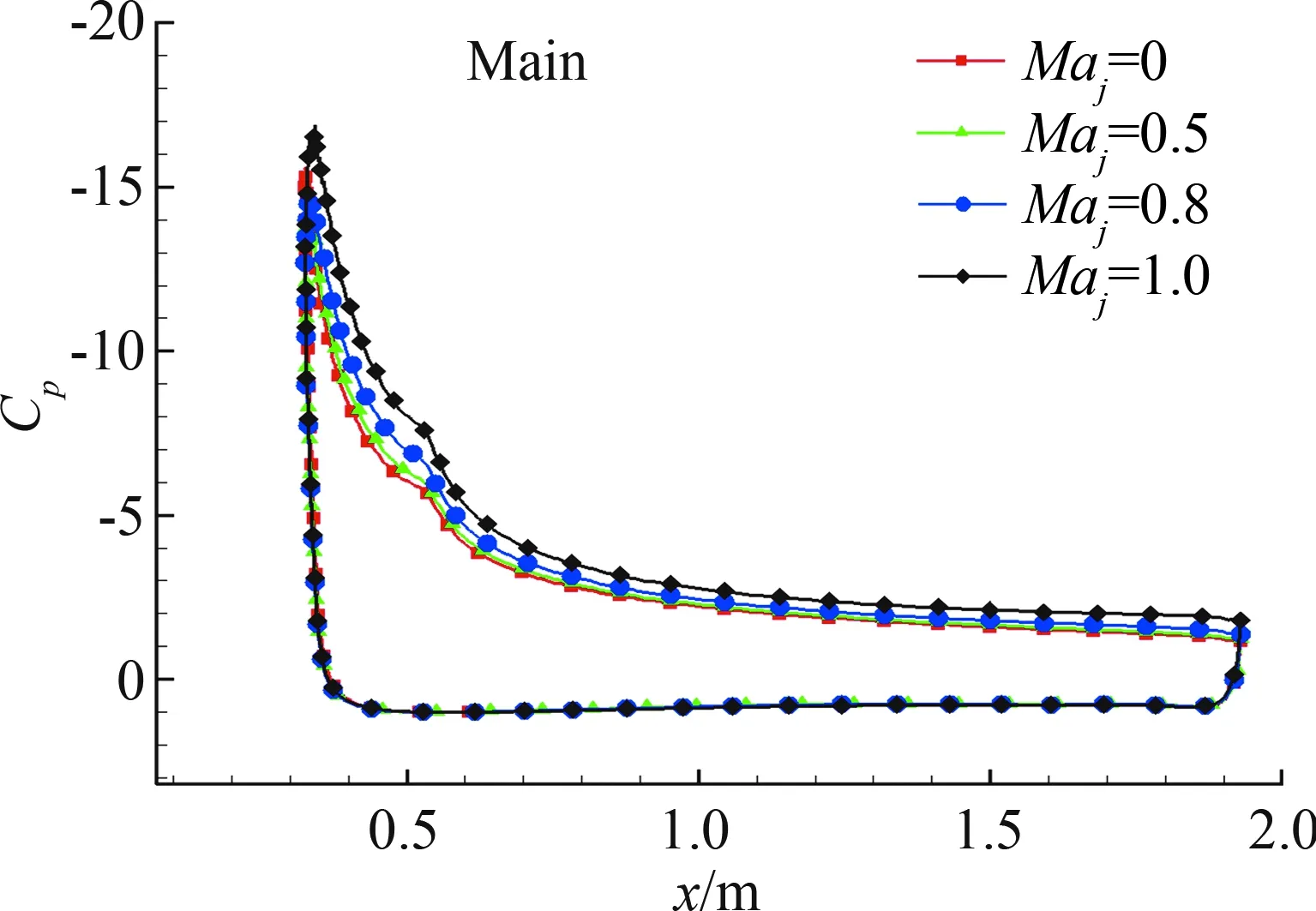
(c) 主翼压力系数

对比分析翼型表面不同站位下的速度型，有助于进一步了解剪切层的改变对各个翼面气动力分布的影响。鉴于篇幅关系，本文仅分析主翼表面的速度型变化。在主翼上表面前缘处选取四个个站位A、B、C和D，分别代表主翼上表面x=0.35 m、x=0.6 m、x=1.0 m和x=1.5 m的位置，示意图如图12所示。

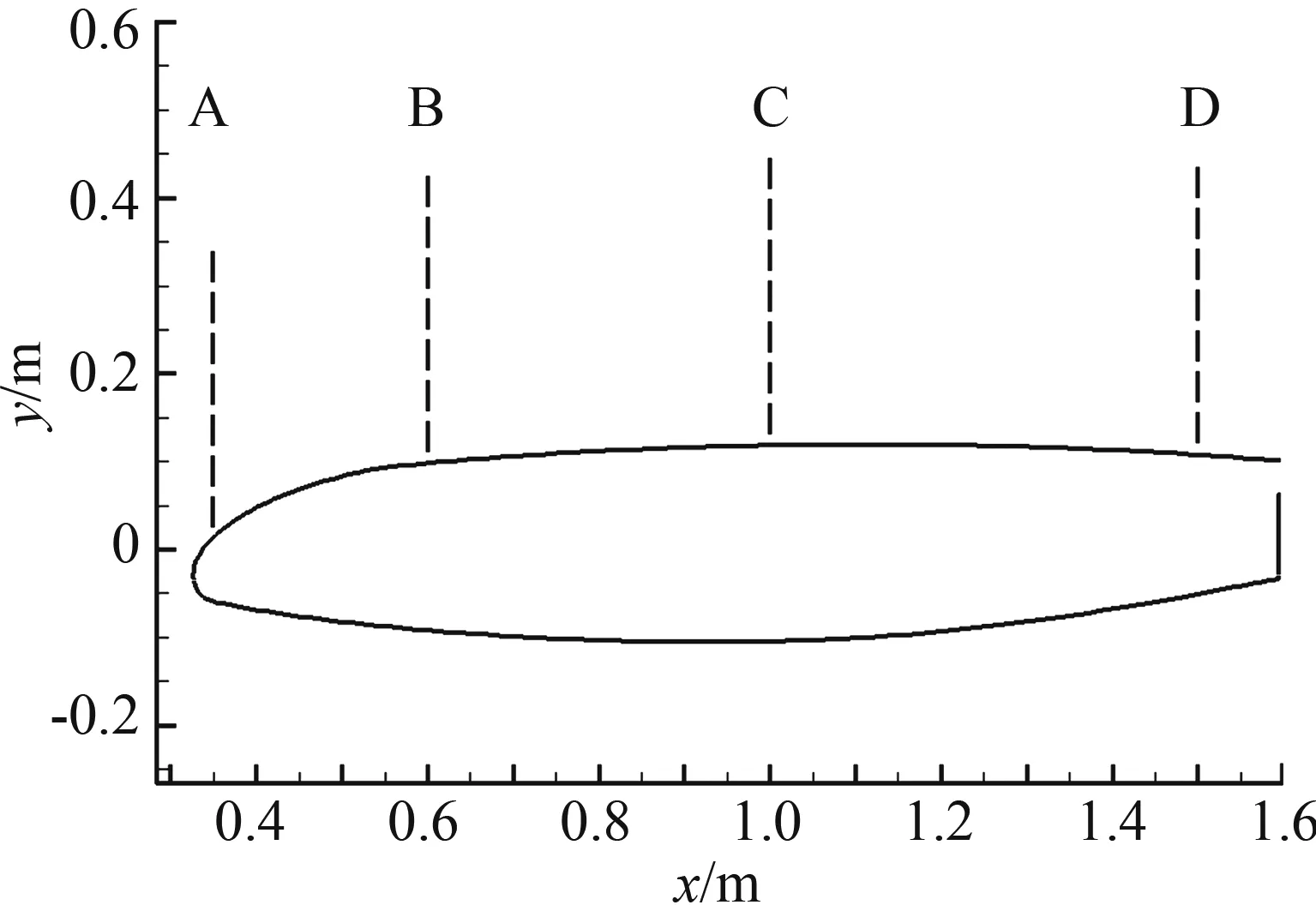
图12 主翼上表面的四个站位Fig.12 Four stations on main element upper surface

对比四个站位下的速度型图13(a～d)发现，沿着翼型弦向，剪切层的改变对主翼表面的影响力逐渐减弱。不同喷流速度影响剪切层厚度以及主翼壁面附近的速度。在主翼前缘附近，喷流速度的提高，能够提高主翼上表面速度，增大主翼表面压力，提高主翼前缘压力峰值，从而提高主翼升力。但随着距主翼前缘弦向距离的增加，剪切层逐渐远离主翼上表面，对主翼表面的速度及压力分布影响减弱。

总体来说，通过增加喷流速度的方式提高喷流动量系数虽然不能使主翼的失速迎角增大，但能够大幅增加各个翼面的升力系数，增加总升力。因此，增加喷流动量系数，对提高多段翼气动性能是十分有利的。

3.2 不同模型添加喷流后的气动力的影响分析

本节研究对Model.1、Model.2和Model.3前缘缝翼尾缘添加相同速度的喷流后，各个翼面升力变化。对比上节的不同喷流速度，在喷流马赫数为1.0条件下各个翼面升力变化最为明显。因此，选择对三个模型Model.1、Model.2和Model.3前缘缝翼尾缘添加喷流的马赫数为1.0，喷流动量系数分别为0.134 5、0.219 5和0.283 6。

(a) 站位A处的速度型

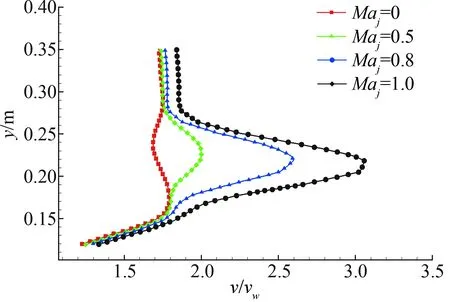
(c) 站位C处的速度型

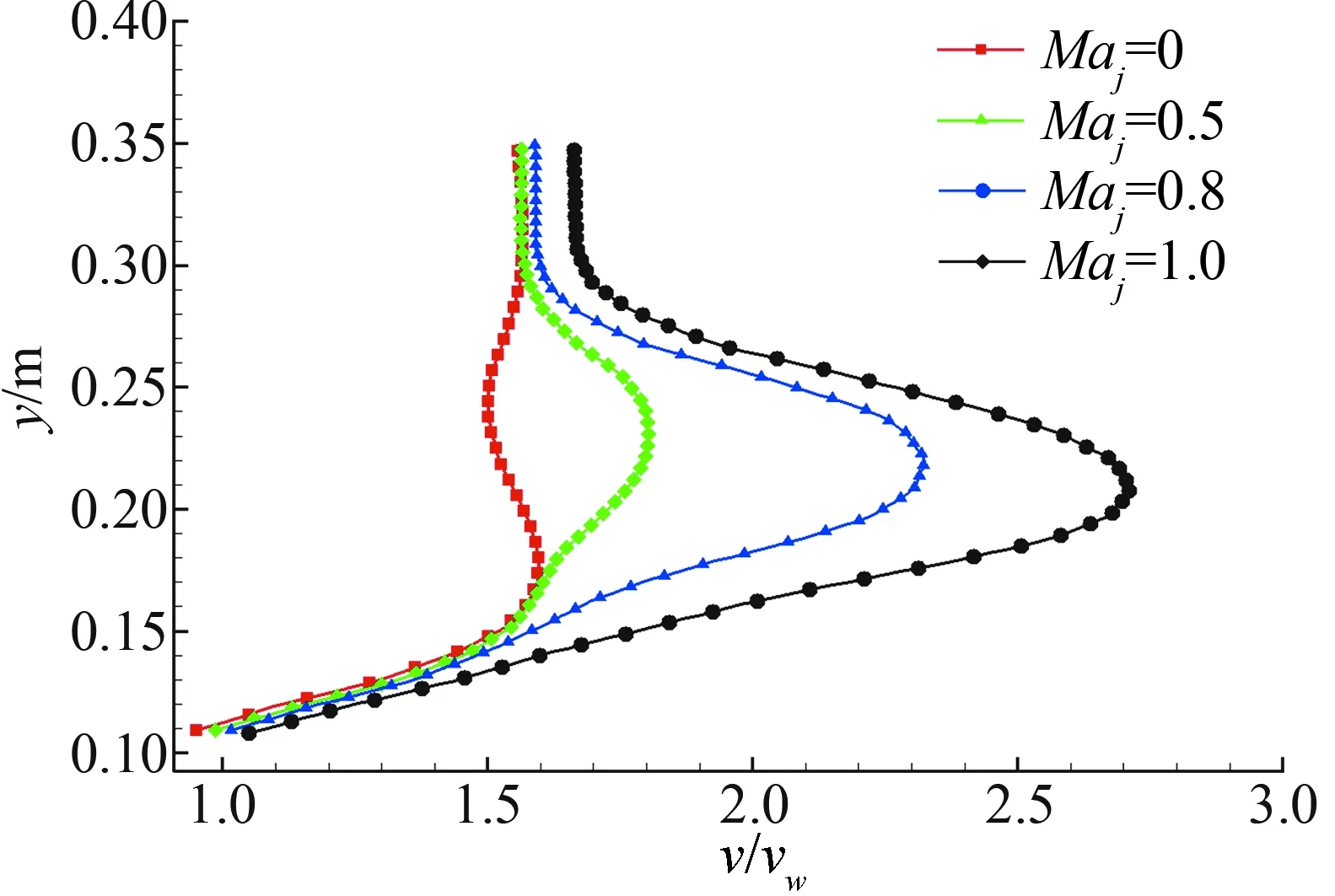
(d) 站位D处的速度型

各个翼面升力变化综合了前缘缝翼缝翼的改变及喷流流量的变化，因此各个翼面的升力变化没有十分明显的规律。但各个模型在前缘缝翼尾缘添加喷流后，后缘襟翼升力系数均较原始模型有了一定的增加，见图14(a)。由后缘襟翼压力分布图15(a)可以看出，添加喷流后，随着喷流动量系数的增加，后缘襟翼负压峰值增大。

由于各个模型前缘缝翼尾缘损失部分不同，前缘缝翼尾缘面积不同，所以喷流流量不同。因此喷流带来的影响包含了前缘缝翼的变化，从压力分布图15(b)来看，喷流对前缘缝翼上下表面的压力影响较小。因此，前缘缝翼尾缘的变化对其升力影响较大，损失的尾缘部分越大，升力减小越大。

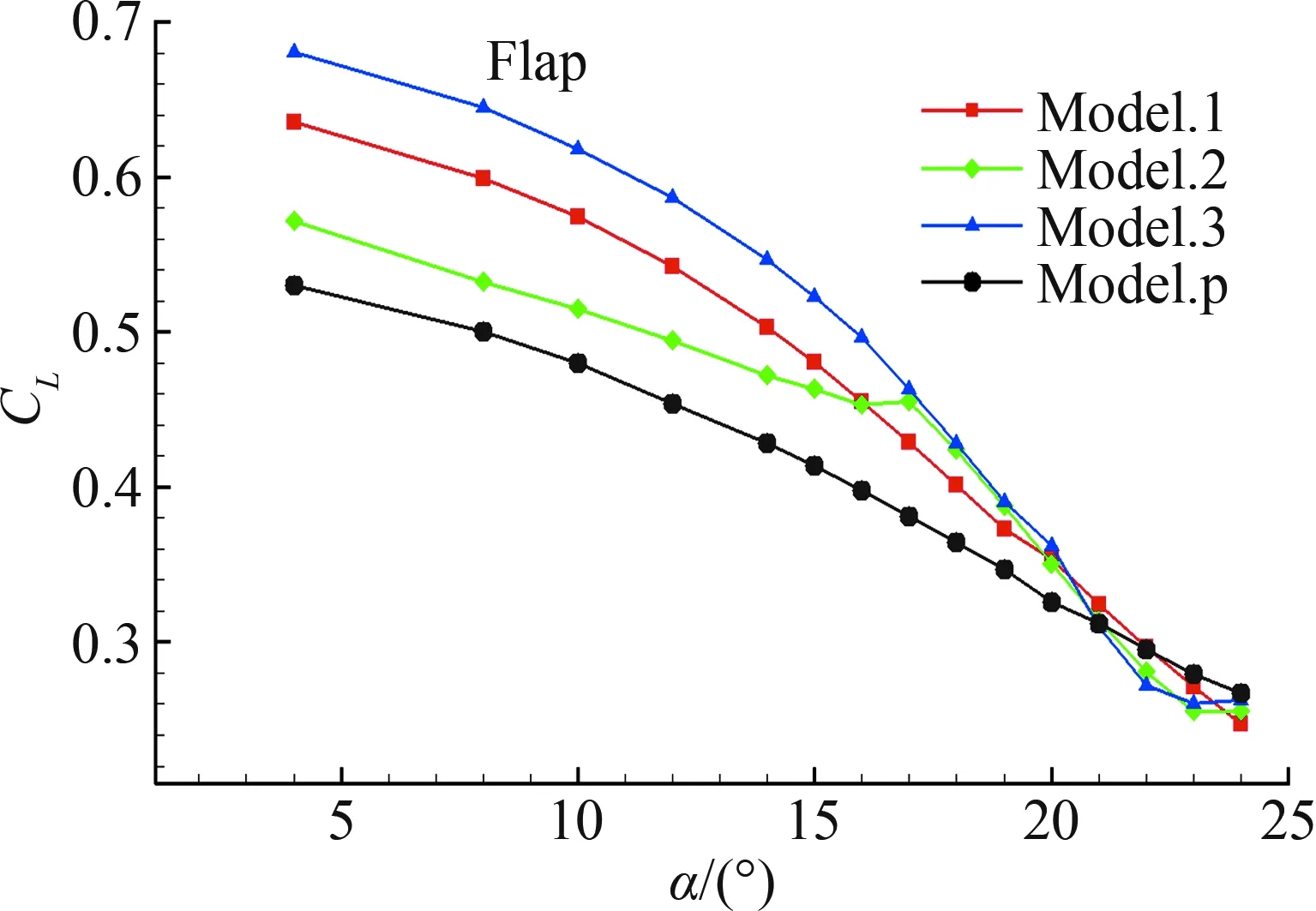
(a) 后缘襟翼升力系

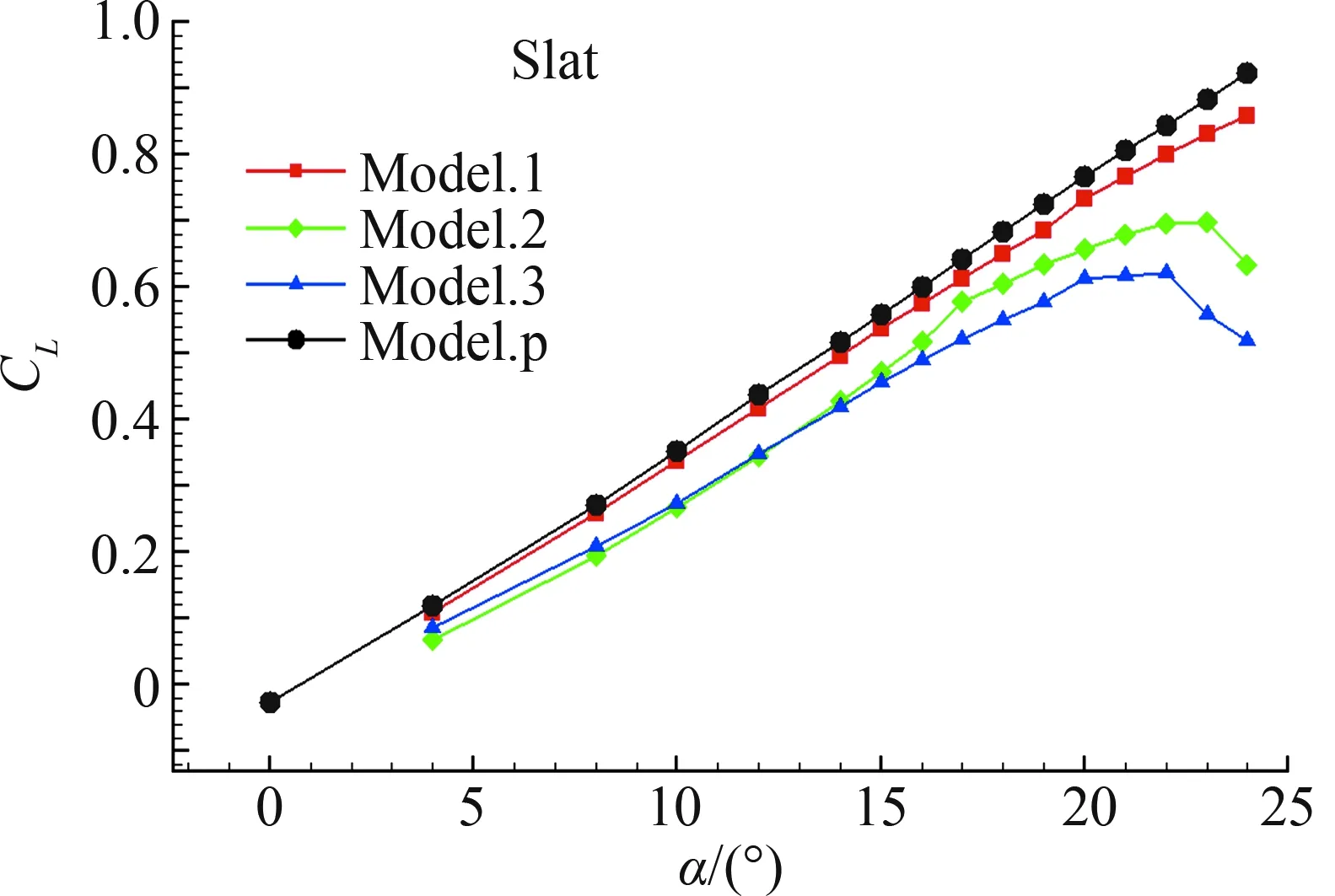
(b) 前缘襟翼升力系数

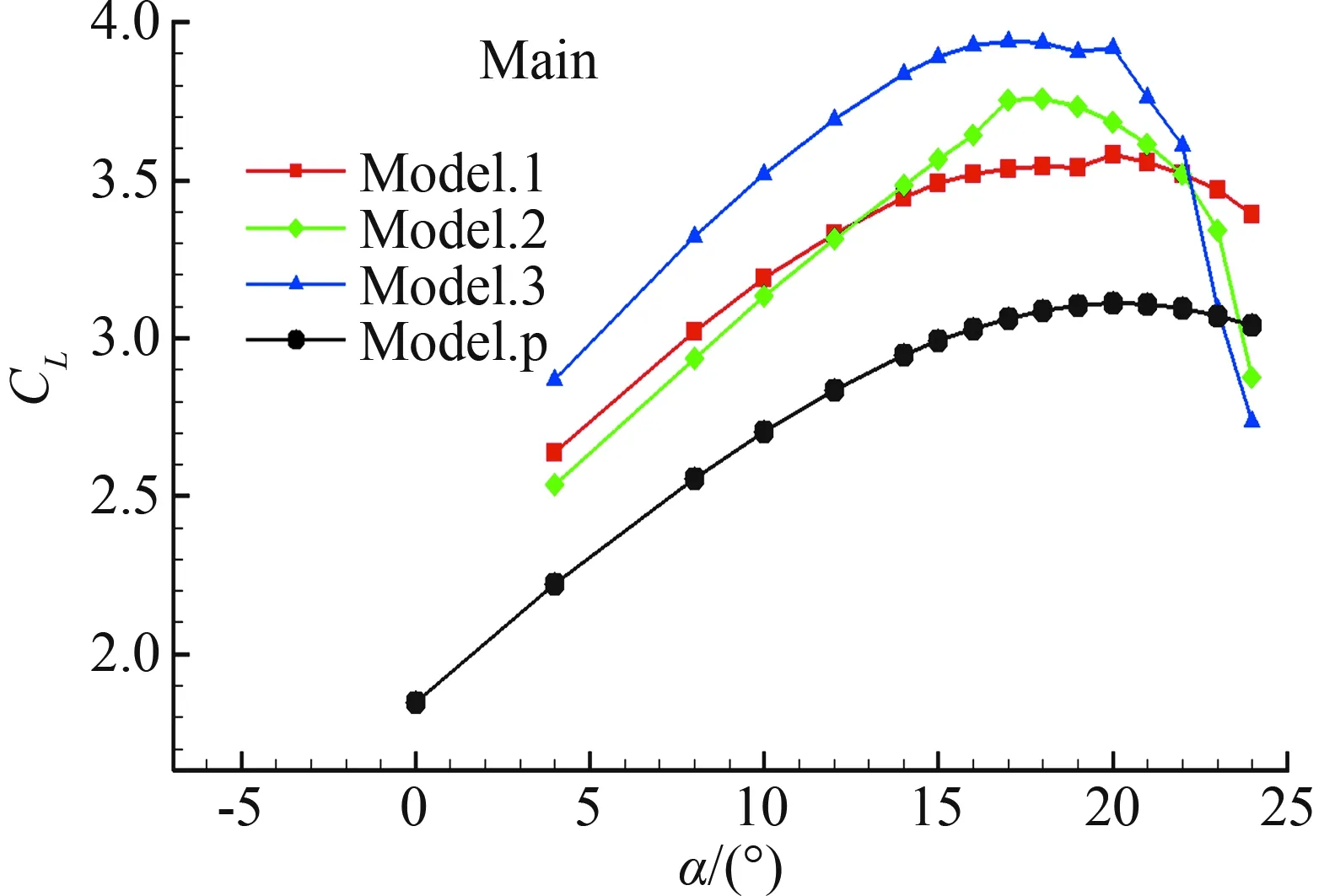
(c) 主翼升力系数

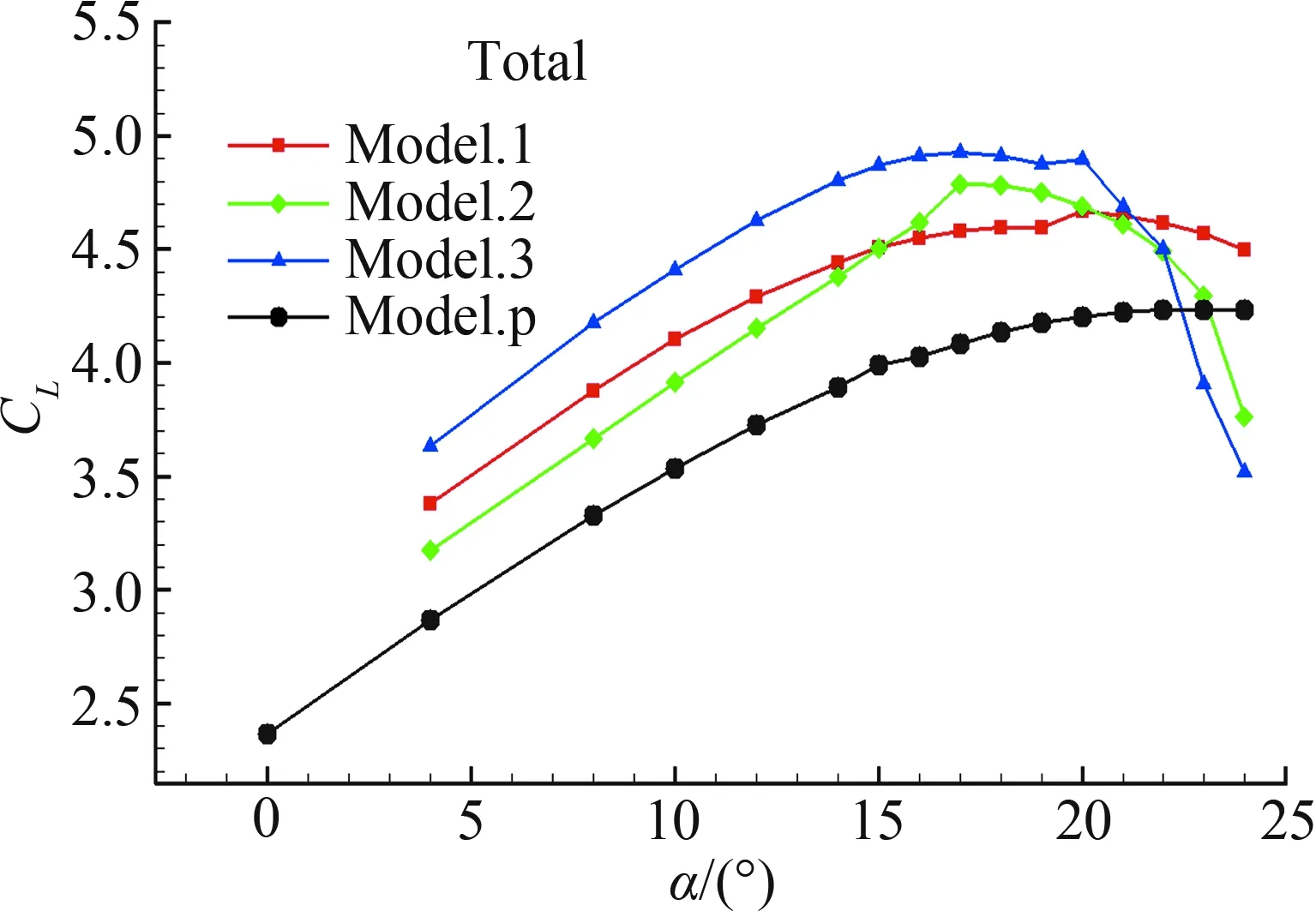
(d) 总升力系数

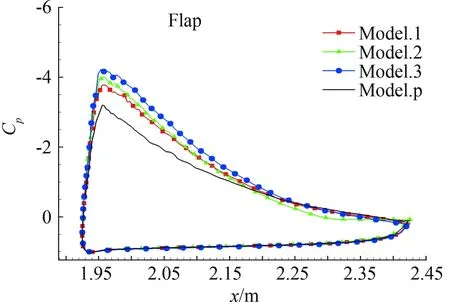
(a) 后缘襟翼压力系数

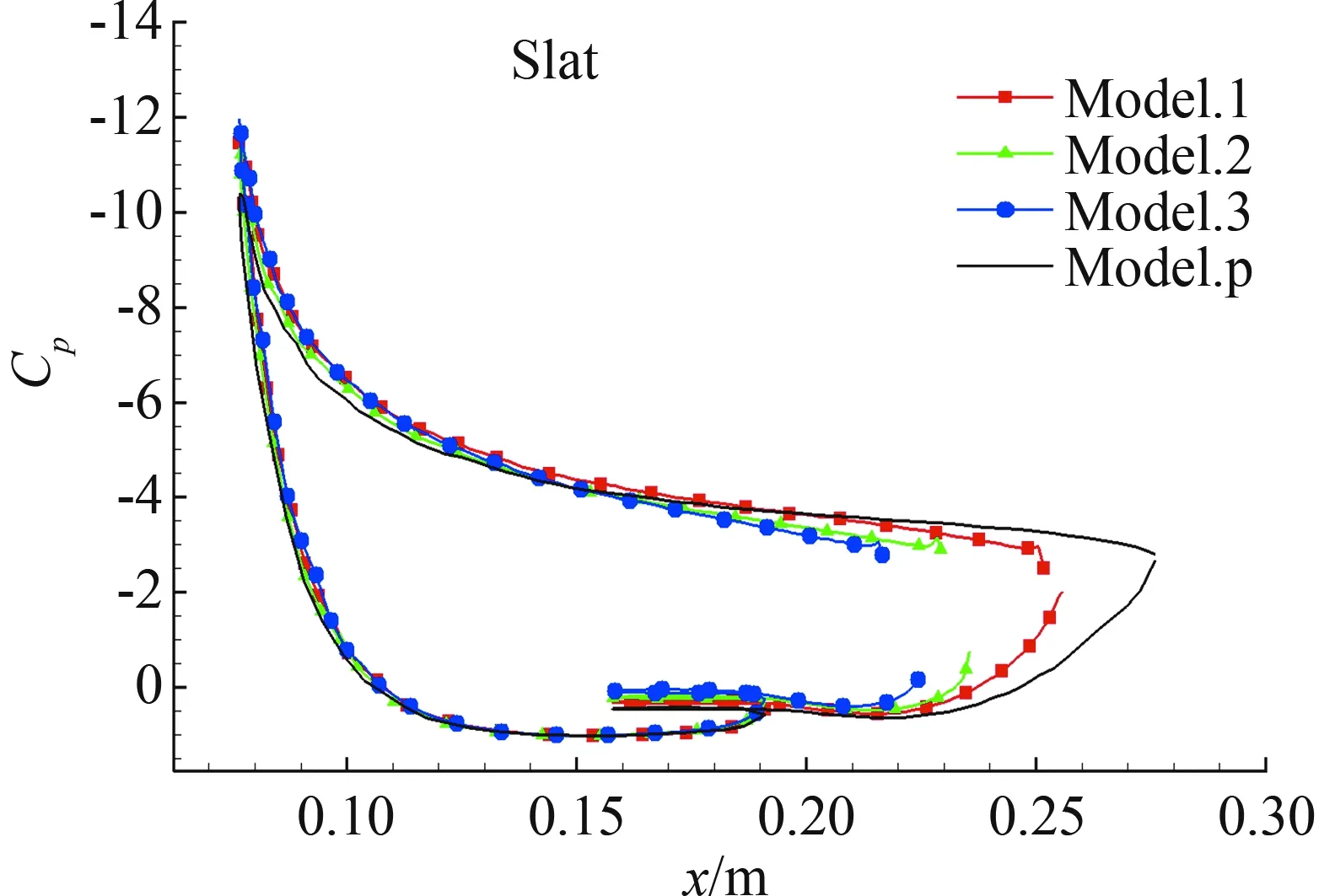
(b) 前缘缝翼压力系数

喷流的添加使得主翼的升力系数有了很大的提升，Model.3主翼的最大升力系数增幅为26.72%，其主要来自主翼上表面的压力提升，如图15(c)。综合三个翼面的升力，喷流大幅提升了总升力的水平，例如,Model.3最大总升力系数增幅为16.31%。总之，喷流能够提升主翼与后缘襟翼的升力水平，因此，喷流的添加对于多段翼增升是有益的。

图16(a)、图16(b)和图16(c)分别为Model.1、Model.2和Model.3的在前缘尾缘添加马赫数为1.0的喷流后流场的速度分布。

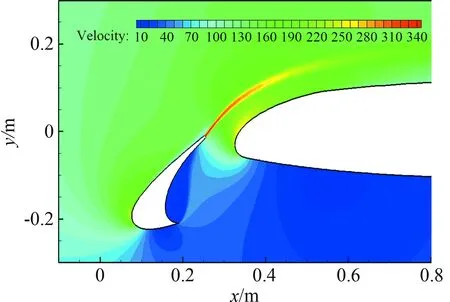
(a) Model.1速度云图

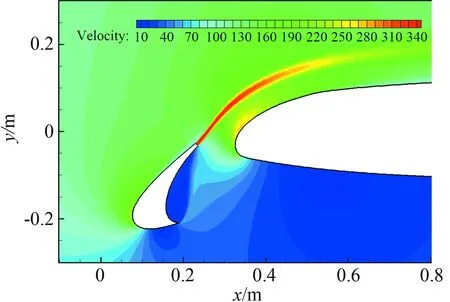
(b) Model.2速度云图

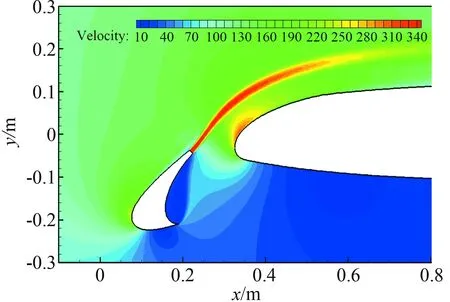
(c) Model.3速度云图

对比Model.1、Model.2和Model.3的速度云图图16(a)、图16(b)和图16(c)发现，在相同的喷流速度下，喷流面积增大，剪切层的厚度增大，喷流影响的区域变大。喷流面积增大，主翼上表面前缘的速度提高较大，具体影响通过主翼上表面的速度型来呈现。对比了两个站位A和B下的速度型图17(a)和图17(b)，由于喷流流量的增加，主翼前缘速度增加较大，且随着流量的增加而增加。喷流动量系数的增加不仅加速了主翼前缘流体的流速，同时也加速了前缘缝翼上表面尾缘处的流体速度，且随着流量的增加，前缘缝翼上表面尾缘流速增加。

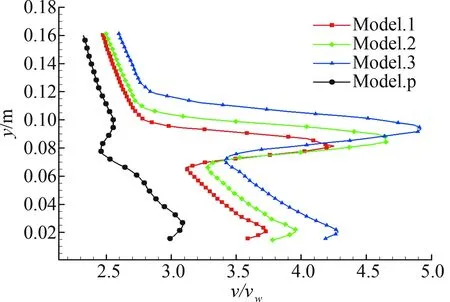
(a) 站位A处的速度型

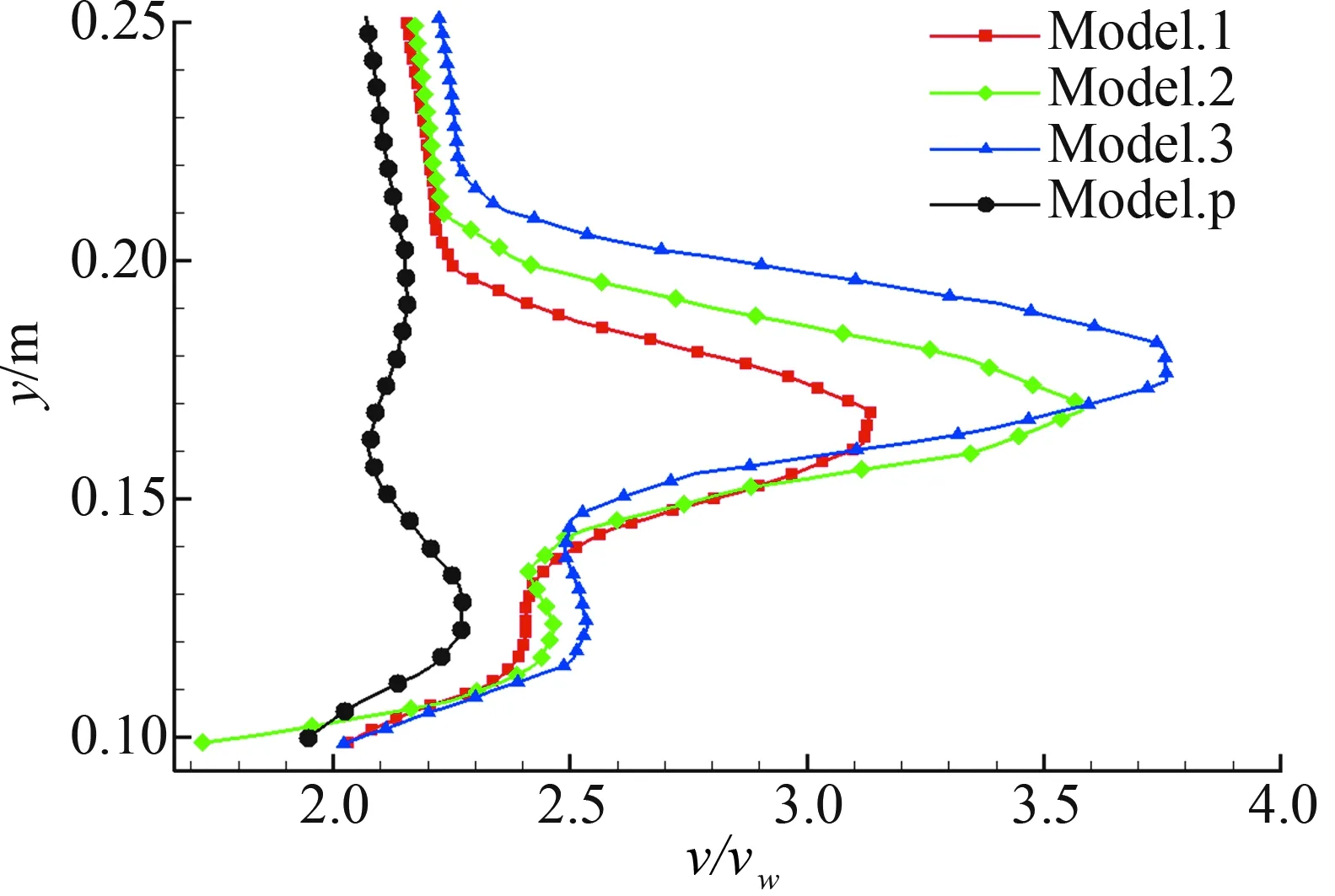
(b) 站位B处的速度型

4 结 论

本文通过数值模拟的方法研究在前缘缝翼尾缘添加喷流后，多段翼各个翼面上的升力及压力分布的改变，得到了如下结论：

1) 前缘缝翼尾缘的喷流对各个翼面的气动力都是有影响的，不同的喷流动量系数会改变尾缘剪切层，进而影响前缘缝翼，主翼以及后缘襟翼表面的压力分布。通过提高喷流速度的方式增大喷流动量系数，能够提升各个翼面的升力系数，同时提高各个翼面的负压峰值，但不能增大主翼的失速迎角。通过增大喷口截面积的方式增大喷流动量系数，会增加各个翼面的升力系数，且随着喷流动量系数增加，前缘缝翼、主翼、后缘襟翼以及总升力系数随之增加，同样的，不能增大主翼的失速迎角。

2) 为了保证前缘缝翼保留部分的上下表面与原模型一致，前缘缝翼尾缘的改变主要通过截取前缘缝翼尾缘来改变弦长和尾缘截面。所以，前缘缝翼尾缘的变化是一个综合的变化，弦长和尾缘截面变化是不可分割。前缘缝翼尾缘的改变影响了前缘缝翼尾缘上表面边界层、下表面边界层和缝道流动。因此，想要单一的分析弦长或者尾缘面积的变化对前缘缝翼尾流影响是一个比较困难的问题，文中没有做详细的研究，也是进一步研究所要考虑的问题。

3) 本文的创新点在于没有延续前人着手于前缘缝翼下表面的改变、缝道参数的改变和主翼边界层的改变。而是利用前缘缝翼的边界层，缝道流动和主翼边界层在前缘缝翼尾缘处相互影响的特点，通过添加喷流的方式改变三者间的相互影响，从而达到改变各个翼面流动的目的。

4) 前缘缝翼的边界层、缝道流动和主翼边界层间的相互影响对多段翼的升力特性以及失速特性均有影响。了解三者相互影响方式和对各个翼面的影响会对分析多段翼提供一个新的视野，通过对三者作用的了解分析，了解缝道流动的实质，也提供一个主动控制前缘缝翼尾流的方向。另外，前缘缝翼喷流的研究对剪切流动研究也提供了一定素材，其数值结果能够为剪切层的研究结果提供一定的数值依据。由于前缘缝翼尾流研究涉及混合，不稳定性发展等等问题，这在不可压剪切流动中都是十分重要的研究方向。因此，这也可以作为稳定性及混合的研究工程实例加以验证。

5) 前缘缝翼尾缘的尾流与前缘缝翼边界层、缝道流动和主翼边界层均相关，添加喷流后对三者的影响尚不清楚，这是一个后期值得研究的一个方向。添加喷流后的尾流，稳定性和混合情况均发生变化，这也是一个值得探讨的课题。因此，后期研究要进一步了解尾流的发展状况，可以从以上几个方面入手。

[1]Thomas C, Martiqua P. Overview of plasma flow control: concepts, optimization and applications. AIAA 2005-563[R]. Reston: AIAA, 2005.

[2]Li Y H, Liang H, Ma Q Y, et al. Experimental investigation on airfoil suction side flow separation by pulse plasma aerodynamic actuation[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1429-1435. (in Chinese)李应红, 梁华, 马清源, 等. 脉冲等离子体气力激励抑制翼型吸力面流动分离的实验[J]. 航空学报, 2008, 29(6): 1429-1435.

[3]Vincent Brunet, Christophe Francois, Eric Garnier, Marc Pruvost. Experimental and numerical investigations of vortex generators effects. AIAA 2006-3027[R]. Reston: AIAA, 2006.

[4]Lin J C. Control of turbulent boundary-layer separation using micro-vortex generators. AIAA-99-3404[R]. Reston: AIAA, 1999.

[5]Lin J C. Review of research on low-profile vortex generators to control boundary-layer separation[J]. Progress in Aerospace Sciences, 2002, (4-5): 389-420.

[6]Liu G, Liu W, Mo B. CFD numerical simulation investigation of vortex generators[J]. Acta Aerodynamica Sinica, 2007, (2): 241-244. (in Chinese)刘刚, 刘伟, 牟斌. 涡流发生器数值计算方法研究[J]. 空气动力学学报, 2007, (2): 241-244.

[7]Ahmed A H. Applications of zero-net-mass jets for enhanced rotorcraft aerodynamic performance[J]. Journal of Aircraft, 2001, 38: 478-485.

[8]Bai J Q, Xin L, Liu N, et al. Numerical simulation of separation control for high Lift system using distributed zero-net mass flux jet[J]. Journal of Northwestern Polytechnical University, 2014, 32(2): 188-194. (in Chinese)白俊强, 辛亮, 刘南, 等. 分布式零质量射流控制增升装置分离的数值模拟[J]. 西北工业大学学报, 2014, 32(2): 188-194.

[9]Gu Y S, Ming X. Investigation on the characteristics and structures of unsteady flow field near the zero-mass flux with PIV[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(1): 83-86. (in Chinese)顾蕴松, 明晓. 应用PIV技术研究“零质量”射流的非定常流场特性[J]. 实验流体力学, 2005, 19(1): 83-86.

[10]Han Z H, Qiao Z D, Song W P. Numerical simulation of active flow control to airfoil stall using local synthetic Jet[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(5): 1040-1046. (in Chinese)韩忠华, 乔志德, 宋文萍. 零质量射流推迟翼型失速的数值模拟[J]. 航空学报, 2007, 28(5): 1040-1046.

[11]Markus S, Thilo K, Frank T. Separation control by self-activated movable flaps. AIAA 2004-1243[R]. Reston: AIAA, 2004.

[12]Kemp H K, Courtney J M, Andrew C, et al. Initial characterization of self-activated movable flaps, “pop-up feathers”. AIAA 2008-369[R]. Reston: AIAA, 2008.

[13]Sean S Z, Qiu Y X. Zhu’s flap and its experimental study in lift enhancement of a wing. AIAA 2004-5080[R]. Reston: AIAA, 2004.

[14]Sean S Z, Qiu Y X. CFD studies on aerodynamic feature of Zhu’s flap. AIAA 2006-3848[R]. Reston: AIAA, 2006.

[15]Sean S Z, Qiu Y X. The aerodynamic feature of a ring wing equipped with Zhu’s flap device. AIAA 2007-4445[R]. Reston: AIAA, 2007.

[16]Fang B R. Aircraft aerodynamic layout design[M]. Beijing: Aviation Industry Press, 1997: 397-426. (in Chinese)方宝瑞. 飞机气动布局设计[M]. 北京: 航空工业出版社, 1997: 397-426.

[17]John M R. A correlation of two-dimensional data in lift coefficient available with blowing-, suction-, slotted-, and plain-flap high-lift devices[R]. Hampton: Langley Aeronautical Laboratory, 1955.

[18]Ibreheem A Q, Mahmood K, Hafez S. Airfoil performance studies with a trailing edge jet flap. AIAA 2013-0239[R]. Reston: AIAA, 2013.

[19]Jiao Y Q, Chen Y Q, Jin C X. Wind tunnel experimental research on lift-enhancing mechanism of jet on wing of aircraft[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(2): 20-24. (in Chinese)焦予秦, 程玉庆, 金承信. 机翼喷流增升机理的风洞试验研究[J]. 实验流体力学, 2008, 22(2): 20-24.

[20]Rumsey C L, Ying S X. Prediction of high lift : review of present CFD capability[J]. Progress in Aerospace Sciences, 2002, 38(2): 145-180.

[21]Chin V D, Peter D W, Spaid F W, et al. Flowfield measurements about a multi-element airfoil at high Reynolds numbers. AIAA-93-3137[R]. Reston: AIAA, 1993.

[22]Mclachlan B G. On the effect of leading edge blowing on circulation control airfoil aerodynamics[R]. Moffett Field: NASA-Ames Research Center, 1988.

Investigation of effects of slat trailing edge jet on multi-element airfoils flowfield

Yang Yin1, Chen Yingchun2, Li Dong1,*

(1.DepartmentofFluidMechanicsofSchoolofNorthwesternPolytechnicalUniversity,Xi’an710072,China;2.ChinaCOMACShanghaiAircraftDesignandResearchInstitute,Shanghai201102,China)

Effect of jet applied to the leading edge slat on the flowfield for multi-element airfoils were investigated to improve the high-lift aerodynamic performance of multi-element airfoils. The influences of key parameters, such as the jet flow rate and the speed of jet on the leading edge slat were studied. CFD method was adopted to analyze the effect of jet on the aerodynamic performance and the shear layer development behind the gap between slat and main element. Two dimensional unsteady Reynolds-averaged Navier-Stokes equations was solved by finite volume method to obtain two dimensional unsteady flowfield of multi-element airfoils. The results indicated that the slat trailing edge jet flow has significant effect on the pressure coefficient of each section of the multi-element airfoils and the maximum lift coefficient simultaneously. The maximum lift coefficient, the total maximum lift coefficient of main element, and the lift coefficients of slat and flap would increase with the jet momentum coefficient increases.

slat; multi-element airfoils; jet; maximum lift coefficient; gap

0258-1825(2017)02-0220-09

2015-05-14;

2015-07-20

杨茵(1985-)，女，回族，新疆昌吉人，博士研究生，研究方向：计算流体力学. E-mail： bates059@sina.com

李栋*,男，博士，教授. E-mail: ldgh@nwpu.edu.cn

杨茵, 陈迎春, 李栋. 前缘缝翼尾缘喷流对多段翼流场的影响研究[J]. 空气动力学学报, 2017, 35(2): 220-228.

10.7638/kqdlxxb-2015.0062 Yang Y, Chen Y C, Li D. Investigation of effects of slat trailing edge jet on multi-element airfoils flowfield[J]. Acta Aerodynamica Sinica, 2017, 35(2): 220-228.

V211.3

A doi: 10.7638/kqdlxxb-2015.0062