关于间接测量的平均值问题探讨
李研海
(吉林省永吉实验高中,吉林 永吉 132200)
关于间接测量的平均值问题探讨
李研海
(吉林省永吉实验高中,吉林 永吉 132200)
物理实验中大多数被测量都是间接测出的,为了减小偶然误差,通常多次测量以平均值作为真实值,究竟是对直接测量量取平均,还是对间接测量量取平均,本文弃繁就简通过案例分析加以研讨,并抒己见.
直接测量; 间接测量; 算术平均值; 线性关系; 离散程度
很多物理量都是间接测量的,所谓的间接测量是指由一个或几个直接测得量经已知函数关系计算出被测量量值的测量.为了减小偶然误差,通常都进行多次测量,并用算术平均值作为测量值,那么究竟是对直接测量量取平均,还是对间接测量量取平均呢?
1 问题由来
1.1 直接间接两可说
物理实验中大多数被测量都不是用仪器直接测出的,在讨论实验原理时,找出此被测量和某些直接测得量之间的函数关系(测量公式),间接测量就是依据此关系,将间接测量转化为若干直接测量,再用直接测量值求出间接测量值.
设间接测得量y=y(x1,x2,…,xm),其中x1,x2,…,xm为不同的直接测得量.现在对x1,x2,…,xm各测量n次.计算间接测量值有两种方法.
方法A:求出各直接测量值的算术平均值,将其代入测量公式,算出间接测量值,即

方法B:从各直接测量值中,分别取一个数值,计算y值,可得n个y值,取其平均值为间接测量结果,即

从理论分析可知,两种方法求出的结果并不一致,但是实际上在大多数情形下,它们的差异甚小或没有差异,因此可根据问题选用一种.
例如,测单摆的摆长l及周期T,求重力加速度g,测量数据见表1.

表1
方法A:g=4π2×101.155/2.0172=981.6016 cm/s2.
方法B:g=(983.50+979.13+975.93+987.91)/4=981.6175 cm/s2.
两方法的差异出现在第5位,对此实验从第5位开始已无意义,因此可认为两种方法的结果是一致的[1].
1.2 直测平均否定说
测定金属电阻率的注意事项: (1) 为了减小金属丝横截面积带来的误差,测量直径时用螺旋测微器在金属丝的3个不同位置各测量1次,取平均值.(2) 测量金属丝的长度应该在接入电路后且在拉直的状态下进行,为减小误差测量3次取平均值.(3) 为了减小实验误差,测量金属丝的电阻时一般电流I、电压U测量多次,求出对应的电阻后取电阻的平均值,不能对U、I取平均[2].
对于间接测量的物理量取平均值问题,第1种观点认为,对直接测量值和对间接测量值两种方法均可.第2种观点中,金属丝的直径、长度及电压、电流同样都是直接测量值,为什么对电压、电流就不能取平均呢?上述两种观点是否矛盾,究竟孰是孰非,在处理实验数据时该怎么做呢?下面我们避开繁难的误差理论,通过具体案例加以分析与探讨.
2 案例分析
案例1.表2是测某一电阻的实验数据,试求待测电阻的阻值.
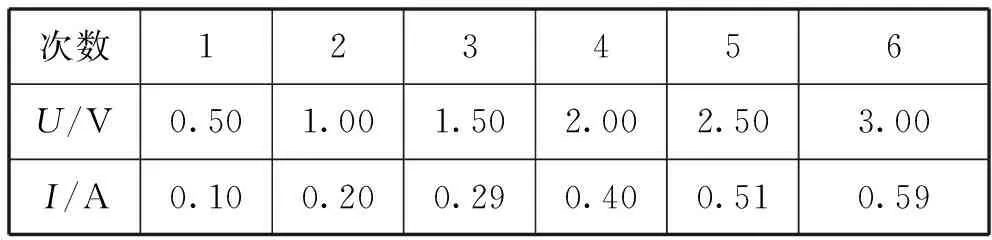
表2 电阻的测量
可见,对于这一实验,无论对直接测量值U、I取平均,还是对间接测量值R取平均,结果几乎是一致的.如果利用实验数据作出U-I图像,可以看出,所有数据点几乎在一条直线上,因此两种方法所得结果几乎相等;倘若所有数据点绝对在一条直线上,那么两种方法所得结果将严格相等,这缘于U与I为线性函数之故.
案例2.表3是测量玻璃砖折射率的实验数据,求玻璃砖的折射率.
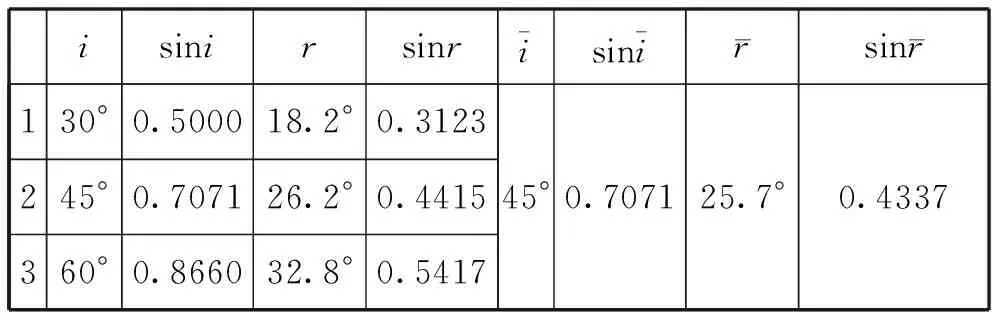
表3 测量玻璃砖折射率
可见,两种方法所得结果明显不同.笔者猜想,这可能是因为正弦函数图像不是直线,折射角r跟入射角i不存在线性关系,即这些角度的正弦值不在一条直线上,所以对角度取算术平均值会出现较大的偏差,并且当几个不同的入射角度取值相差越大,所求的结果偏差就越大,反之越小.

可以看出,两种方法所得结果几乎相等,从而证明上述猜想是正确的.
案例3.表4是用单摆测定重力加速度的实验测量数据,试求重力加速度的数值.

表4 用单摆测定重力加速度
解法3:对间接测量值g取平均,有g1=9.800000 m/s2,g2=9.800000 m/s2,g3=9.7999995 m/s2,则加速度平均值为
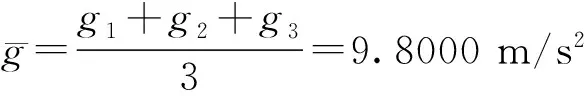
需要说明的是,在上述运算中,为了防止截尾引入的误差过大而掩盖问题的本质,因此参与运算的数字都保留了较多的位数.可以看出,对直接测量值取平均与对间接测量值取平均所得结果明显不同,这是因为时间t或周期T跟摆长l呈非线性函数的缘故,倘若几次实验的摆长相近,两种方法所得结果也必相近,如果是对同一摆长进行几次测量,两种方法所得结果则几乎相等.
3 笔者之见
3.1 取平均值注意的问题
取平均值必须注意3个问题,即对哪个量取平均、取何种平均(算术平均值、几何平均值、调和平均值、加权平均值等)以及在什么范围内取平均,本文所谓的平均皆指算术平均值,且在不同范围内取平均所得结果往往不同.
3.2 两种观点不矛盾
“直接间接两可说”中方法A,是指对同一条件(几个直接测量值的离散程度极小,一般不超过仪器的最小分度值)下的几个直接测量值取平均值.原例中是作者对摆长约为101.1cm(同一条件)的条件下进行的几次摆长和周期测量,由于读数的偶然误差导致实验测量数据各异;对不同条件(几个直接测量值的离散程度很大)下的几个直接测量值取平均,实非作者本意,不可曲解,若任意加以推广可能会出现问题,有时甚至显得荒谬.
前述的“直测平均否定说”中,测定金属电阻率实验,测金属丝直径和长度时,是对同一条件(直径和长度未变)的直接测量值取平均.而测电阻时是对不同条件(不同电压、电流)下间接测量值取平均,一般来说是不可行的,不过在这一实验中对电流和电压取平均也未尝不可.
3.3 两种平均勿滥用
从上述的案例分析可知,无论何种情况,对间接测量值取平均总是切实可行的.而对直接测量值取平均是有条件的.
(1) 只有当两个直接测量值存在线性关系时,既可以对间接测量值取平均,也可以对直接测量值取平均,且在多大范围内取平均都行(与离散程度无关).
(2) 当两个直接测量值不存在简单的线性关系,例如指数函数、对数函数、三角函数等,对不同条件下的直接测量值,在大范围内取平均,将会引起较大的误差;只有当所测的几个直接测量值极为接近时(离散程度较小),即较小范围内才可以对直接测量值取平均.对同一条件下的几个直接测量值取平均值是完全可以的.
就物理实验中的间接测量而言,对间接测量值取平均最为稳妥可靠,且无条件限制,对不同条件下的几个直接测量值取平均,务必慎重,最好不用,但并非绝对不行,只不过有条件限制.关键是正确理解,灵活运用.
1 杨述武.普通物理实验(一、力学·热学部分)第2版[M].北京:高等教育出版社,1990:30-31.
2 杜志建.试题调研特辑·高考5年真题分类详解物理[M].乌鲁木齐:新疆青少年出版社,2013:129.
2016-11-28)

