函数可积性教学的改进策略
韩新方,马 丽*
(1.海南师范大学 数学与统计学院,海南 海口 571158;2.海南省数学研究中心 海南师范大学,海南 海口 571158)
函数可积性教学的改进策略
韩新方1,2,马 丽1,2*
(1.海南师范大学 数学与统计学院,海南 海口 571158;2.海南省数学研究中心 海南师范大学,海南 海口 571158)
文章对不同数学分析教材中函数可积性内容的编排及若干定理的证明进行了比较分析,给出了新的教学内容安排.证明了只有有限个间断点的有界函数在闭区间上是可积的.
可积性;教学安排;新证明
很多《数学分析》教材[1-3]在给出函数可积的定义后,对随后内容分如下三部分叙述:(i)函数可积的充分必要条件;(ii)几类可积函数;(iii)可积函数的性质.其中(i)为讲解可积函数类以及可积函数的性质奠定了基础.许多《数学分析》教材关于函数可积性的论述是在达布和的基础上给出函数可积的充要条件[1-12],也有教材从函数可积的定义出发直接证明函数可积的柯西准则[13].这些教材给出函数可积的定义以后,接着安排函数可积充要条件的学习和证明,在逻辑上是合理的,数学素养高的同学能较快地理解函数可积是什么以及如何判定函数可积.但是把函数可积定义为某种形式的极限存在,相当于利用高等数学中极限概念定义一个新的概念,会使数学素养不够或者基础不扎实的同学有些茫然.而接下来讲解达布上和、达布下和以及柯西判断准则等复杂而抽象的内容,更使这一部分同学学起来感觉吃力.本文探讨了一种新的教学安排,希望能够分散教学内容中的难点,从而降低数学分析初学者的认知难度.关于函数的可积性有如下两个基本定理:定理I,连续函数在闭区间上可积;定理II,只有有限个间断点的有界函数在闭区间上可积.本文将在给出新的函数可积性的教学安排之后给出定理II的一个新证明.
1 几种教材关于定理I、定理II证明的比较
华东师范大学数学系主编的《数学分析》[10]以及袭怀云等主编的《数学分析》[9](其他参看[1-8,11])对第一个基本定理(定理I)的表述为:
利用连续函数f(x)在闭区间[a,b]一致连续及定积分的定义容易得到函数 f(x)在[a,b]上可积.李忠等主编的《数学分析教程》[13]运用达布上和与达布下和的性质证明了定理I:
定理2 设函数y=f(x)在[a,b]上连续,则y=f(x)在[a,b]上黎曼可积.
因为教材[13]在此定理之前没有叙述可积的充要条件,所以对此定理的证明回到定义,即证明函数 f(x)在闭区间[a,b]上的黎曼和的极限存在.运用达布上和与达布下和的性质,得出闭区间[a,b]上的连续函数f(x)在[a,b]中的上积分和下积分相等,且都等于黎曼和的极限.
在前一种类型的教材的教学安排中,连续函数可积等内容是放在讲解函数可积的充要条件之后的,证明思路也大同小异.数学基础扎实的同学容易接受这样的教学安排.后一种类型的教材,抛开了振幅的概念,引入了达布上、达布下和,但是跟前一种利用振幅无限小的证法没有本质上的区别,相比于前一种证法反而增加了(达布上和和达布下和等)新的概念,无形中也增加了学生的负担.
对于第二个基本定理(定理II),刘玉琏主编的《数学分析》[6]证明了如下定理:
定理3 如果函数f(x)在[a,b]上有界,且只有有限个间断点,则函数 f(x)在[a,b]上可积.
先假设 f(x)在[a,b]上只有一个不连续点c(a<b<c).取c的任意ε小邻域内,利用函数的有界性,及f(x)在其余区间上的任意部分区间Δxi上的振幅wi能一致的小于ε,于是有故 f(x)在[a,b]上可积.对于有限个不连续点的情况,证法类似.
陈传璋等人主编的《数学分析》[1]也可参看[3,5,9])先给出了函数可积的若干个充要条件,进而运用其中一个充要条件证明了定理II:
定理4 只有有限个第一类不连续点的有界函数是可积的.
证明中利用的充要条件为:函数 f(x)在[a,b]上可积的充要条件是任给正数ε,η,总存在某一个分割T,使得属于T的所有小区间中,对应于振幅wi≥ε的那些小区间Δxi的总长∑TΔxi<η.
2 关于函数可积性的新教学安排及定理II的新证明
本文对几种教材进行分析之后发现:部分教材[10]给出了可积的充要条件,却没给出证明(在教材后面章节中进行补叙或留给学生自己证明).这样的安排使得学生对可积充要条件的理解不够深入;还有一部分教材[1]把若干可积的充要条件放到一起讲,这虽然比较适合研究型的学生,但对于刚开始接触数学分析的大多数本科生来说,这些证明太繁琐,理解起来相对吃力.另外,大部分教材关于定理II只证明了可积性,没给出明显的积分值.
基于上述考虑,本文给出如下新的教学安排:首先给出函数可积的定义,接着讲可积函数的基本性质[13],再讲定理I和定理II的证明.有了这些基本的认识之后,再安排讲解函数可积的充要条件等内容,且可以根据不同生源情况适当取舍,安排不同深度和广度的讲解.下面给出定理II的一个新证明.
定理5 如果函数f(x)在区间[a,b]上有界且只有有限个间断点,即 f(x)在[a,b]上有界且逐段连续,则在由间断点分割[a,b]所得的各个小区间上 f(x)可积,且f(x)在[a,b]上的积分等于 f(x)在以上每个小区间上积分的和.
证明 设f(x)在[a,b]上有n个间断点{xi,i=1,…,n},下面分两种情况来证.
(1)区间端点不是间断点的情况.
假设a=x0<x1<…<xn<xn+1=b,构造如下函数列{fi(x),i=0,1,…,n}

其中,i=0,1,…,n.则fi(x)在区间[xi,xi+1]上连续,所以fi(x)在区间[xi,xi+1]上可积.令
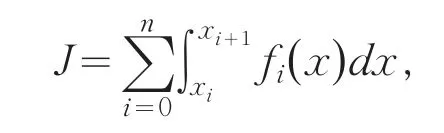
设存在一个常数M,使得∀x∈[a,b]有|f(x)|≤M.对任意[a,b]上的分割T来说,f(x)在区间[a,b]上的黎曼和为这里Δxk=xk+1-xk,ξk是区间[xk,xk+1]上的一个点.由积分的定义、极限和无穷小的关系(见[6,13]等)知,(其中是分割T和区间[xi,xi+1]相交的部分,ε为任意小的常数).将积分和∑Tf(ξk)Δxk分为不包含间断点的积分和与包含间断点的积分和两部分,于是有

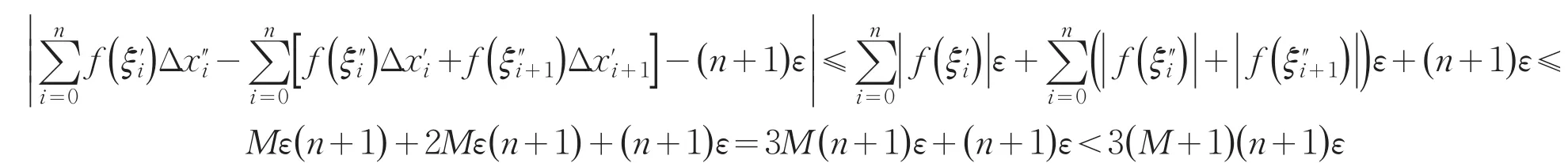

(2)当区间的两个端点有一个为间断点或者两个都是间断点时,证明过程与(1)类似.
[1]陈传璋,金福临,朱学炎,等.数学分析[M].北京:高等教育出版社,1983.
[2]陈纪修,於崇华,金路.数学分析[M].北京:高等教育出版社,1999.
[3]李成章,黄玉民.数学分析[M].北京:科学出版社,2004.
[4]南京师范大学.数学分析选论[M].南京:江苏教育出版社,1988.
[5]许绍溥,姜东平,末国柱,等.数学分析教程[M].南京:南京大学出版社,1990.
[6]刘玉琏.数学分析[M].北京:高等教育出版社,1994.
[7]华中师范大学数学系.数学分析[M].武汉:华中师范大学出版社,2000.
[8]解可新,刘九兰,邱忠文.分析与近世代数基础[M].天津:天津大学出版社,2000.
[9]龚怀云,刘跃武,陈红斌,等.数学分析[M].西安:西安交通大学出版社,2000.
[10]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.
[11]周民强.数学分析[M].上海:上海科学技术出版社,2003.
[12]刘玉琏,傅沛仁,林玎,等.数学分析讲义[M].北京:高等教育出版社,2003.
[13]李忠,方丽萍.数学分析教程[M].北京:高等教育出版社,2008.
[14]高英敏.关于振幅的等价定义[J].青海师专学报(教育科学版),2003,23(6):15-16.
责任编辑:吴兴华
The Improvement Strategy of Functional Integrality Teaching
HAN Xinfang1,2,MA Li1,2*
(1.School of Mathematics and Statistics,Hainan Normal University,Haikou571158,China;2.Hainan Center for Mathematical Research,Hainan Normal University,Haikou571158,China)
In this article,we compare the arrangements of the contents of integrability of functions on different versions of mathematical analysis and propose a new teaching arrangement on these contents.It also gives a new proof of the following theorem:bounded functions with finite discontinuous points are integrable on closed intervals.
integrability;teaching arrangement;new proof
G 420;O 172.2
A
1674-4942(2017)01-0105-03
2016-09-21
国家自然科学基金(11326169);海南省高等学校教育教学改革研究项目(HNJG2014-22)
*通讯作者:马丽,副教授,E-mail:malihnsd@163.com
10.12051/j.issn.1674-4942.2017.01.017

