飞机舵机电液伺服系统多余力抑制方法研究

刘晓琳+殷健敏

摘 要：针对飞机舵机电液伺服系统在加载过程中出现易出现加载频宽窄，响应速度慢、稳定性差、加载精度低等问题，采用BP神经网络PID控制与结构不变性原理相结合的控制方法。该方法基于BP神经网络的参数自整定原理调节系统参数，再根据结构不变性原理控制器。仿真结果表明，该控制方法不仅能有效抑制多余力的干扰，而且可以显著提高飞机舵机电液伺服系统的控制性能。

关键词：飞机舵机电液伺服系统；BP神经网络；PID控制；结构不变性原理；多余力

1 概述

飞机在飞行过程中依靠操纵面的摆动产生空气气动力或力矩，从而改变飞行器的飞行姿态。飞机舵机是控制飞机操纵面实现飞行姿态的重要部件，其性能的好坏事保证飞机可靠并有效运行的关键环节[1]。为了便于研究飞机舵机的性能，通常在实验室条件下建立飞机舵机电液伺服系统模拟飞机在实际飞行过程中所受到各种力载荷[2]，完成飞机舵机性能的相关测试。该方法不仅可以有效调节载荷梯度，能够对非线性力载荷进行模拟加载，而且可以对舵机进行实时协调加载，更加符合飞机舵机对实时性的要求。因此，研究高精度的飞机舵机电液伺服系具有重要的现实和战略意义[3]。

由于飞机舵机电液伺服系统是典型的被动式力伺服控制系统，在加载过程中，存在稳定性差、准确定低以及跟踪效果不理想等影响[4]。因此，如何通过设计系统的控制方法，有效抑制多余力，是保证飞机舵机电液伺服系统精度和性能的基础。目前国内外很多学者都十分重视电液伺服系统的发展，也得到了政府的资助，并且一直是液压控制领域的一个前沿课题。

2 系统的结构组成

飞机舵机电液系统结构如图1所示。整个系统主要由两部分组成：加载系统和飞机舵机。

3 系统数学模型

3.1 电液伺服阀模型建立

电液伺服阀阀芯位移与控制输入之间的传递函数为：

3.2 液压缸模型建立

为了便于系统研究，采用线性化方法描述动力元件的非线性微分方程[5]。加载阀的线性方程为：

式中，QL为负载流量；Kq为滑阀流量增益；xv为伺服阀阀芯位移；Kc为伺服阀滑阀流量压力放大系数；PL为负载压力。

液压缸的流量连续性方程为

式中，Ap为活塞面积；xp为活塞位移；Vt为液压缸两腔的总容积；？茁e为油液的弹性模量；Ct为总泄漏系数。

液压缸和负载力平衡方程为

式中，Mt为活塞及由负载折算至活塞上的总质量；Bp为活塞及负载等运动件的黏性阻尼系数；KL为负载运动时的弹簧刚度；FL为作用在活塞上的其他负载力。

3.3 橡胶缓冲弹簧模型建立

橡胶缓冲弹簧所传递的力与活塞和飞机舵机的位移之差成线性比例关系[6]，其力传感器的方程为：

FL=KL（xp-y） （5）

式中，y为舵机位移。

由式（2）至式（5），可以得到液压缸和阀芯的位移传递函数为

由式（1）至公式（6），可以得到系统的传递函数为：

通过式（7）分析可知，多余力的产生因素与舵机位移、速度、加速度及其导数等因素有关使得系统力载荷指令信号出现相位滞后和幅值误差，导致飞机舵机电液伺服系统性能较差。

4 飞机舵机电液伺服系统控制方法设计

为了确保加载系统能够快速准确地输出加载力，建立飞机舵机电液伺服系统数学模型，设计合理的控制策略是提高系统性能和抑制多余力的重要前提。

（1）利用BP神经网路PID控制器的原理对系统性能进行提高。

（2）采用飞机舵机速度信号作为补偿器输入，不仅将信号源补偿在干扰信号出现之前，而且可以减小噪声干扰，避免微分项放大噪声影响系统工作，消除小加载梯度下多余力干扰明显的问题，从而提高系统的加载精度和稳定性。

4.1 BP神经网络PID控制

经典的PID控制器，由比例（P）、积分（I）、微分（D）3个部分组成，PID 控制器的工作原理是根据系统最初设定信号r（t）与实际输出信号y（t）两者之间产生偏差信号e（t），再将偏差信号 进行比例、积分、微分运算后，通过线性方式组合在一起输出最终的控制信号，实现对硬件系统的闭环控制。其控制系统原理如图2所示。

由于控制计算机接收到信号为离散的数字控制，根据采样时刻的偏差值计算控制量，使用的是数字PID控制器。通常采用增量式数字PID控制算式，其控制算法如下：

4.2控制器设计

由于多余力的产生具由超前性，因此选择飞机舵机运动指令信号作为信号源，结合其基本原理如图4所示。

由公式（7）分析可知，为了消除式中多余力项，整个系统的传递函数为：

5 仿真实验及结果分析

利用MTALAB计算机仿真实验，验证多余力抑制的有效性。

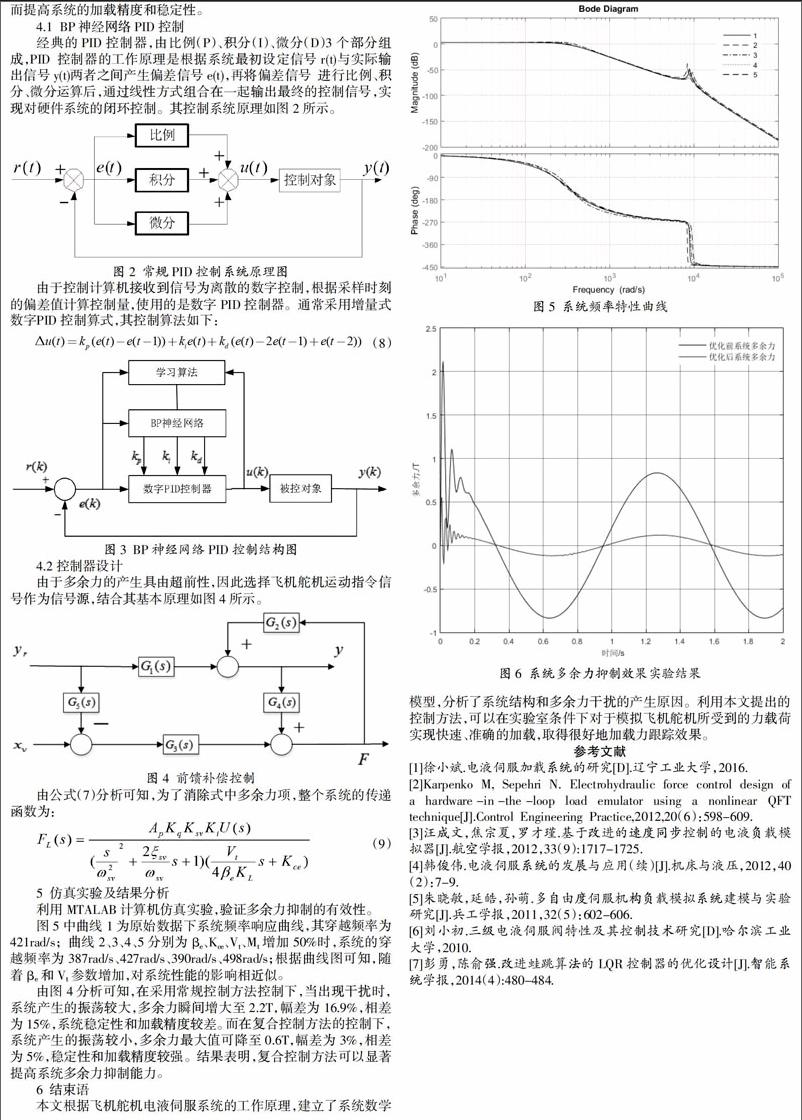
图5中曲线1为原始数据下系统频率响应曲线，其穿越频率为421rad/s； 曲线2、3、4、5分别为？茁e、Kce、Vt、Mt增加50%时，系统的穿越频率为387rad/s、427rad/s、390rad/s、498rad/s；根据曲线图可知，随着？茁e和Vt参数增加，对系统性能的影响相近似。

由图4分析可知，在采用常规控制方法控制下，当出现干扰时，系统产生的振荡较大，多余力瞬间增大至2.2T，幅差为16.9%，相差为15%，系统稳定性和加载精度较差。而在复合控制方法的控制下，系统产生的振荡较小，多余力最大值可降至0.6T，幅差为3%，相差为5%，稳定性和加载精度较强。结果表明，复合控制方法可以显著提高系统多余力抑制能力。

6 结束语

本文根据飞机舵机电液伺服系统的工作原理，建立了系统数学模型，分析了系统结构和多余力干扰的产生原因。利用本文提出的控制方法，可以在实验室条件下对于模拟飞机舵机所受到的力载荷实现快速、准确的加载，取得很好地加载力跟踪效果。

参考文献

[1]徐小斌.电液伺服加载系统的研究[D].辽宁工业大学，2016.

[2]Karpenko M， Sepehri N. Electrohydraulic force control design of a hardware-in-the-loop load emulator using a nonlinear QFT technique[J].Control Engineering Practice，2012，20（6）：598-609.

[3]汪成文，焦宗夏，羅才瑾.基于改进的速度同步控制的电液负载模拟器[J].航空学报，2012，33（9）：1717-1725.

[4]韩俊伟.电液伺服系统的发展与应用（续）[J].机床与液压，2012，40（2）：7-9.

[5]朱晓敏，延皓，孙萌.多自由度伺服机构负载模拟系统建模与实验研究[J].兵工学报，2011，32（5）：602-606.

[6]刘小初.三级电液伺服阀特性及其控制技术研究[D].哈尔滨工业大学，2010.

[7]彭勇，陈俞强.改进蛙跳算法的LQR控制器的优化设计[J].智能系统学报，2014（4）：480-484.