大惯量下电动伺服机构非线性特性与控制方法研究

张新华,黄 建,张兆凯,段小帅,刘 源

(北京自动化控制设备研究所,北京 100074)

大惯量下电动伺服机构非线性特性与控制方法研究

张新华,黄 建,张兆凯,段小帅,刘 源

(北京自动化控制设备研究所,北京 100074)

针对高超声速飞行器非线性影响飞行姿态控制问题,分析了电动伺服机构中传动间隙、刚度、摩擦力矩等非线性因素的影响,并讨论了由间隙引起极限环的定义及产生条件。针对传动间隙引起的极限环振荡和较大惯量的翼面加剧振荡问题,建立了系统间隙极限环模型和非线性振动模型,并提出了间隙补偿器设计方法。重点研究了间隙、翼面转动惯量、刚度及干扰力对伺服控制系统的影响规律。通过在内环增加间隙补偿器的基础上,在外环引入速度、加速度负反馈设计方法,解决了大惯量舵面下控制系统抖动问题,仿真和试验结果证明了这一理论是正确的。

电动伺服机构；极限环；间隙；刚度；非线性振荡

0 引言

电动伺服机构是电动伺服系统的控制对象,也是伺服系统的重要组成部分。性能优良的电动伺服机构应具有结构谐振频率高、负载转动惯量最小、传动间隙小、传动精度高、传动效率高等特点。电动伺服机构一般包括放大器、电机、减速机构及反馈元件。系统的稳定性、瞬态和稳态性能受到系统阻尼、固有频率、增益以及转动惯量的影响。而这些参数由组成系统的各环节的特性所决定,且受到放大器死区、机械间隙、机械刚度及摩擦等非线性因素的影响,这些非线性因素的存在将导致系统性能的变化,尤其是大惯量负载下非线性因素对控制系统带来的影响[1-4]。文献[5]用间隙描述函数和动量定理,分析了含间隙系统驱动大惯量负载时产生的极限环振荡问题。文献[6]通过线性补偿以及参数调整的方法来抑制非线性影响,其效果有限。文献[7]进行了基于舵机系统复刚度特性的舵面颤振特性分析,指出复刚度的幅值和相位角是影响颤振边界的重要因素。随着现代控制方法的发展,自适应、变结构、智能控制等也用来抑制非线性影响,但其控制方法相对复杂[8-9]。本文针对某型号导弹翼面发生抖动的问题,从伺服系统结构和控制算法两方面着手,对舵机传动间隙、刚度和翼面转动惯量造成系统非线性振荡进行了深入研究,并提出解决措施。

1 间隙模型及分析

1.1 间隙模型

伺服系统的非线性主要为饱和与间隙,针对间隙非线性,目前主要有迟滞模型、死区模型和振-冲模型[10-12]。对于电传伺服系统,其相位滞后对控制系统影响比较大,所以在此以迟滞模型来描述舵机间隙。

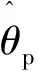
(1)

式中,θ为输入转轴转角；θp为输出转角；2α为间隙大小,m为系统传动比。

舵机间隙对控制系统性能有很多不利影响,主要有：

1)降低系统稳定性。当舵机间隙达到一定值时,系统产生极限环振荡,此时系统的动态性能与稳定性显著下降,控制效率降低。

2)使系统产生相位滞后,影响系统快速性。间隙越大,相位滞后越严重,对控制系统相位裕度的要求越高。

3)降低了舵机系统的定位精度,使控制系统产生一定的稳态误差。

4)由于间隙存在,机构承载时会有冲击现象,降低了机构可靠性,间隙较大时可能使系统响应超调。

1.2 极限环理论及补偿模型

对于平面系统：

(2)

有闭环轨迹Γ,若存在δ>0使系统在Γ的两侧相邻域S(Γ,δ)内的一切轨迹以S(Γ,δ)为其Ω或极限集A,则称Γ为系统的极限环,即在某连通区域存在独立闭轨迹的系统存在极限环。由Dulec 判定法和Bendixson判定法可以判定极限环的存在[11]。

从控制理论分析,是系统内部非线性环节增加的奇点使系统相轨迹出现了闭轨,从而产生极限环；从物理结构分析,由于非线性特性作用,使系统能从非周期性的能源中获取能量以维持其周期运动。针对舵机间隙,当舵机主动轮转向时,需先越过2倍的间隙,不直接驱动负载,导致能量积累。当主动轮越过间隙重新驱动负载时,积累能量的释放将使负载运动变化剧烈。当间隙过大,储能过多,则会引起系统的极限环振荡。图1所示为某系统的开环频率特性曲线—奈奎斯特图。图2所示为复平面上的间隙非线性负倒描述函数-1/N(A)的曲线,函数曲线位于复平面的第三象限,其与实轴的交点为(-1/k,j0),不同的k值对应不同的曲线①、②和③。若曲线与频率特性曲线相交,那么至多产生2个交点A和B,至少产生1个交点C。2条曲线相交的含义是伺服系统因为间隙非线性的原因产生了极限环振荡,振荡的频率和幅值分别对应频率特性曲线上的交点相应值。为解决上述问题,依据间隙补偿模型,引入前馈非线性补偿,得到系统的逆变换如下：

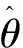
(3)

式中,θd(t)为舵机期望值输出值；g(τ,t)=2αδ(τ-t)为2α垂直跳跃；δ(t)为Diracδ函数。

图1 开环频率特性曲线Fig.1 The open-loop frequency characteristic curve

图2 复平面上非线性负倒描述曲线Fig.2 The negative curve in the complex plane

按照非线性补偿控制,其结构如图3所示,基于该补偿方法的某舵系统小惯量下的阶跃、斜坡仿真曲线如图4所示。从图4可知,阶跃和斜坡仿真中,逆间隙补偿系统能有效地改变间隙所引起的振荡和误差。

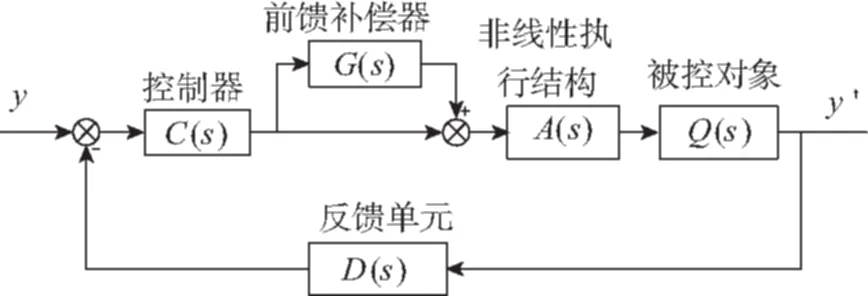
图3 加前馈补偿器原理图Fig.3 The schematic diagram of feed forward compensator

(a)逆间隙补偿系统阶跃响应

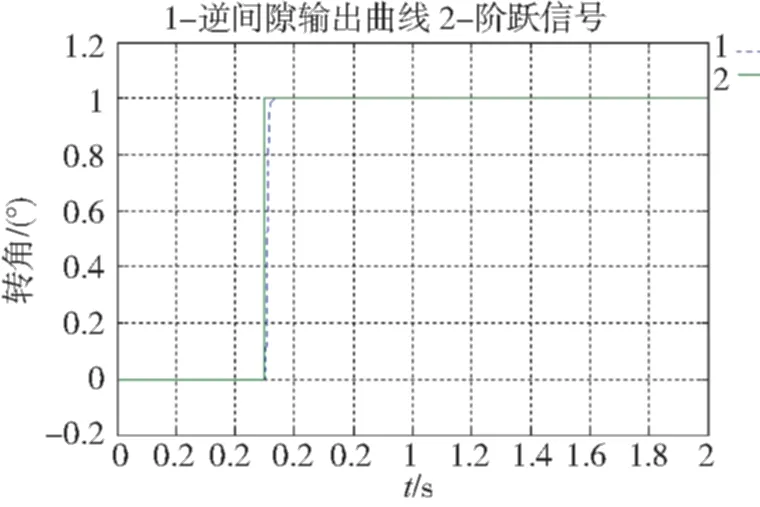
(b)未加逆间隙补偿系统阶跃响应

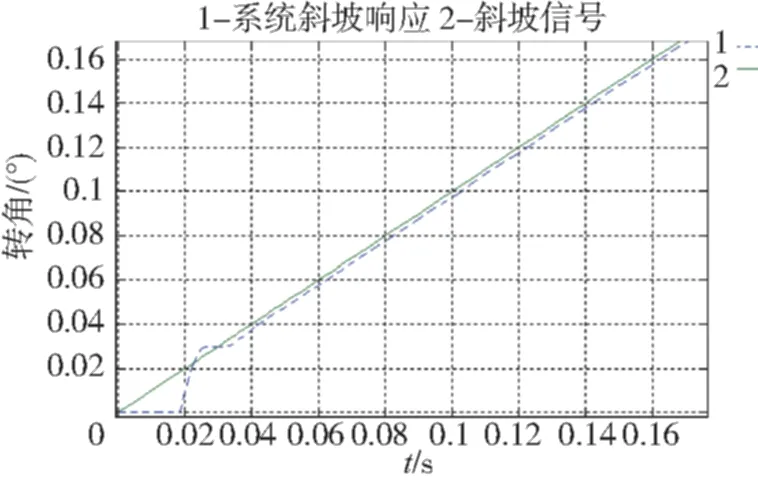
(c)加逆间隙补偿系统斜坡响应

(d)未加逆间隙补偿系统斜坡响应图4 系统阶跃响应Fig.4 The system step response

2 刚度分析

刚度是指整个伺服系统表现出来的抵抗外部扰动转矩产生微位移偏差的能力。按照外加负载力的交变与否,分为静刚度和动刚度。刚度的好坏将直接影响伺服系统对动态干扰的抑制能力,若伺服系统刚度低、惯量大,则难以获得较高的转动速度,同时还产生较大的失动量,使传动误差增大,影响系统定位精度；由于各传动部件之间存在间隙、摩擦、弹性变形,以及控制系统死区、电动机运行误差等因素引起的失动量,导致伺服机构滞后或引发振荡。伺服系统的刚度是确定预紧力大小,并最终决定摩擦和传动间隙大小的主要因素。研究提高电动伺服系统的刚度,对于提高位置伺服系统的定位精度具有很重要的意义。

下面仿真某舵系统刚度试验,设置某系统舵机的间隙为0.15°,滚珠丝杠副的结构静刚度分别为107N·m、1.55×107N·m。控制指令保持为0°,在舵机输出轴处施加交变负载,分别测量交变负载在不同频率时,转矩幅值依次为80N·m、90N·m、100N·m、110N·m、120N·m、130N·m、140N·m、150N·m下的动刚度。仿真的结果如图5～图6所示。

图5 伺服动刚度仿真图Fig.5 The servo stiffness simulation

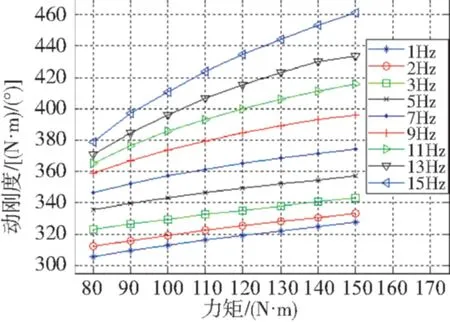
图6 变结构刚度后伺服动刚度仿真图Fig.6 The variable structure servo stiffness simulation

由图5、图6可知,系统的伺服动刚度与舵机的结构刚度有关,在一定范围内,舵机的结构刚度越大,系统的伺服动刚度越大；在系统的带宽内,系统的伺服动刚度与负载转矩的频率有关。

3 运动信息融合控制算法

常规的位置伺服系统主要采用位置、速度、电流进行三环控制,在存在非线性因素环节下,效果并不佳。而对于间隙补偿模型,比较适用于小惯量负载舵系统应用场合,但对于大惯量伺服系统,还需要综合考虑间隙、翼面转动惯量、伺服刚度及干扰力对伺服控制系统的影响。传统PID控制效果并不理想,容易造成系统超调量大,且系统容易产生抖动现象。大惯量下伺服系统的加速度控制将对系统产生重要的影响,它直接决定系统的跟随性与稳定性,如能对系统速度和加速度进行补偿控制,那么就能有效地改善系统的动态特性,并能抑制谐振产生。本文控制通过在内环增加间隙补偿器的基础上,在外环引入速度和加速度负反馈设计方法,解决了大惯量下系统抖动问题。

建立伺服系统摩擦、刚度、惯量的综合等效开环传递函数如下

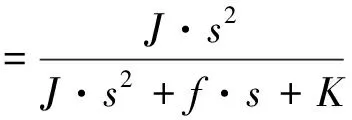
(4)

式中,J表示负载转动惯量(kg·m2),f表示摩擦(N·m),K表示系统等效刚度(N·m)/(°)。

因此,可得出其闭环传递函数G(s)

(5)

(6)

式中,A表示位置滤波后的加速度信息；B表示位置滤波后的速度信息；C表示位置滤波后的位置增益信息。考虑非线性振荡特性,引入补偿变量α1、α2、α3,其中：α1表示加速度加权因子,α2表示速度加权因子,α3表示位置增益加权因子。因此,通过调节α1、α2、α3参数来实现系统的最优控制。

4 仿真与试验分析

4.1 仿真分析

以某伺服系统进行仿真,电机额定电压270V,电机电阻0.12Ω,电感0.9mL,电机额定功率3.5kW,额定转速11000r/min,转矩系数0.2(N·m)/A,额定转矩3.5 N·m,滚珠丝杆减速比270,电机转动惯量3.5×10-5kg·m2,负载额定转动惯量0.4kg·m2,电位计增速比为2∶1。舵系统指标要求额定转矩≥700N·m,最大转矩≥1000N·m,额定转速≥200(°)/s,带宽≥15Hz@-3dB且相位-90°,静态误差≤2%,半振荡次数≤2。通过建立的电动系统仿真模型,得到系统无惯量额定转矩负载下仿真波形和额定惯量额定转矩负载下系统仿真波形。

从图7可知,通过选择合理的位置、速度、电流增益系数和反馈系数,系统在无惯量额定转矩下,动态性能较好,具有较快的响应速度,上升时间为103ms,速度可达242(°)/s,系统无超调现象,稳态误差为0.21°,无抖动现象。从图8可知,在相同的控制参数及控制方式下,当在额定惯量额定转矩下进行实验时,系统出现明显的抖动现象,抖动幅值为1.2°,谐振频率为22Hz,可见,系统的抗扰动性能差,通过多组PID参数验证,仍出现相同的现象,因此,传统的PID控制系统不能满足指标要求。

图7 无惯量额定转矩负载下跟踪曲线Fig.7 Rated load torque traces with no inertia

图8 额定惯量额定转矩负载下跟踪曲线Fig.8 Rated load torque traces with rated inertia

依据该伺服系统性能指标要求,依次设定加权因子α1=0.03、α2=5.2、α3=0.15,位置环增益系数kp=36,位置环反馈系数kf=1,速度环增益系数ks=1.2,电流环增益系数ki=0.8,得到系统额定惯量额定转矩下25°阶跃系统仿真波形,图9所示为额定惯量引起的瞬态冲击响应,图10所示为多元运动信息融合补偿下系统跟踪曲线。

图9 额定惯量下25°引起的冲击响应曲线Fig.9 25° impulse response curve on rated inertia

图10 额定惯量额定转矩下25°阶跃跟踪曲线Fig.10 25° response curve on rated load and inertia

从图9图可知,在0.4kg·m2惯量下,最大将引起1.7°冲击值,抖动持续时间达180ms,产生的冲击响应影响非常大,因而在控制方法不合理的情况下,容易引起抖动现象。采用多元信息融合补偿后,从图10可知,该系统在惯量额定转矩下,具有好的动态和静态特性,具有较快的响应速度,上升时间为101ms,速度可达247(°)/s,静态误差为0.17°,系统无超调无谐振现象。

4.2 试验分析

1) 间隙影响

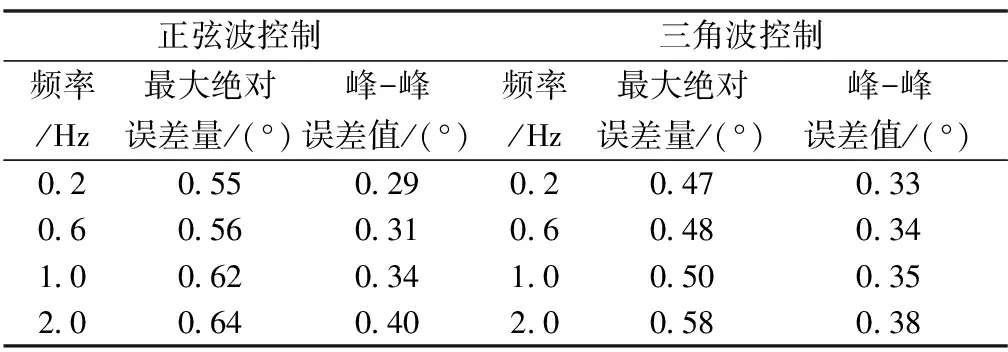
通过采用输入低频小幅值正弦信号和三角波信号观察系统跟踪曲线,确定间隙对系统输出特性的影响。鉴于实验条件限制,主要采用小摩擦条件下(100N·m)间隙值0.2°进行实验研究,试验结果如图11～图12所示,并在不同频率段采用相同的实验方法得到数据如表1所示。

图11 1Hz正弦位置跟踪曲线Fig.11 The sine location tracking curve on 1Hz

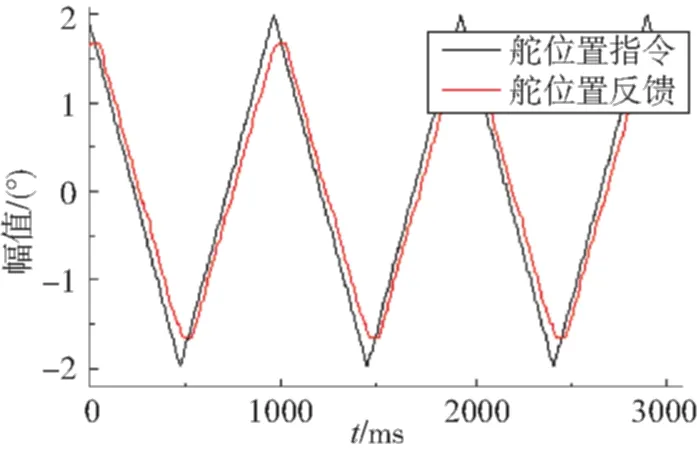
图12 1Hz三角波位置跟踪曲线Fig.12 The triangle location tracking curve on 1Hz

正弦波控制三角波控制频率/Hz最大绝对误差量/(°)峰-峰误差值/(°)频率/Hz最大绝对误差量/(°)峰-峰误差值/(°)0205502902047033060560310604803410062034100500352006404020058038

从表1可知,间隙存在下,当系统超量小时,必将引起平顶现象, 0.2°间隙下最大误差量为0.64°,峰峰值误差为0.40°。误差值随控制频率的增加而增加,这与系统的响应速度有密切关系,可见间隙量的大小直接影响到系统的静态指标,也影响到系统的动态特性。

2)惯量影响

本文以相同的控制方式,分别在空载和额定惯量下进行间隙实验。图13所示为小间隙额定惯量空载下幅值25°阶跃位置跟踪波形,图14所示为小间隙额定惯量弹性转矩下幅值25°阶跃位置跟踪波形。

图13 空载下25°阶跃波形Fig.13 25° step waveform without load

从图13可知,在额定惯量空载下,幅值25°阶跃时,系统超调2.65%,1个半波后系统稳定,系统稳定误差为0.08°,上升时间为110ms,速度227(°)/s。从图14可知,当在额定惯量弹性转矩下,25°阶跃时,系统超调1.2%,一个半波系统稳定,稳态误差为0.22, 上升时间112ms,速度223(°)/s。因此,在小间隙额定惯量条件下,系统具有较好的动态和静态特性,满足总体技术指标要求。

为验证在惯量条件下间隙对系统的影响,通过调节传动机构的预紧力,增加系统传动机构的间隙。基于间隙实验基础,分别在额定惯量弹性转矩0.2°间隙和0.3°间隙下进行实验,图15所示为0.2°间隙额定惯量弹性转矩25°阶跃位置跟踪曲线,图16所示为0.3°间隙额定惯量弹性转矩下25°阶跃位置跟踪曲线。

图14 弹性转矩下25°阶跃波形Fig.14 25° step waveform with elastic load

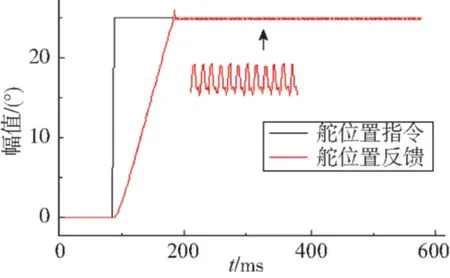
图15 0.2°间隙25°阶跃位置跟踪曲线Fig.15 25° location tracking curve on 0.2° clearances

图16 0.3°间隙25°阶跃位置跟踪曲线Fig.16 25° location tracking curve on 0.3° clearances

从图15可知,上升时间为115ms,速度217(°)/s,当到达末端时,系统出现抖动现象,谐振的频率大约为38Hz,幅值为0.21°,超调量5.8%；从图16可知,上升时间为119ms,速度210(°)/s,抖动频率为42Hz,幅值为0.42°,超调量7.8%,幅值有所增加,可见随着间隙量的加大,系统更加容易出现抖动现象。因此,惯量存在下间隙存在将直接影响系统的稳定性。

随着间隙的增大等效固有频率减小,即不同的间隙产生了不同的固有频率,这点既可以解释负载在不同位置处的振动频率为什么不同,也能说明间隙越大越容易产生谐振。

前面讨论了惯量存在下间隙对系统稳定性的影响,但如果系统承载的惯量低于系统加载的惯量,那么也能引起系统的不稳定性,造成系统出现抖动现象。为验证惯量的影响,在小间隙条件相同的控制算法下,通过对系统施加不同的惯量研究其稳定性,图17所示为对系统施加0.5kg·m2惯量弹性转矩下25°阶跃跟踪曲线。

图17 弹性转矩下25°阶跃跟踪曲线Fig.17 25° location tracking curve with elastic load

从图17可知,系统在到达目标位置后,舵机将产生抖动现象,抖动的频率为34Hz,幅值为0.45°,超调量9.2%。表2所示为小摩擦不同惯量下系统性能指标。

表2 不同惯量下系统性能指标

从表2可知,在小惯量时,系统动态和静态性能较好,但是随着负载惯量的增加,稳定性将降低,可见惯量的增加也影响了系统的稳定性。随着翼面转动惯量的减小,系统的谐振峰频率逐渐增大,这可以解释翼面转动惯量越小,系统的固有频率越高,则发生谐振的可能性越小[2]。

3)传动比影响

电动伺服系统的控制性能与机械传动比也有重要的关系,在设计系统时,应综合考虑电机转速、电机输出力矩、负载力矩、系统动态特性等参数和指标来优化设计。对于大惯量系统,机械传动比越大控制系统越不容易抖动；但是,传动比过大会造成系统动态特性的降低,如采取提高电机转速来解决该问题,会使电机特性变柔软,反而不利于控制。传动比过小,引起输出力矩小,不满足要求,且系统容易抖动。因此,在满足系统动态特性的前提下,可以提高传动比来改善系统性能。

5 结论

电动伺服机构中传动间隙、刚度、摩擦力矩等非线性因素对系统性能均有重要影响。本文针对舵机间隙非线性设计了前馈非线性补偿器,从理论上解决了间隙非线性补偿问题,指出了刚度对系统的影响。在实际大惯量负载下,控制系统的性能与系统摩擦、刚度等非线性因素之间还有复杂的联系,仅仅依靠补偿器并不能完全解决控制系统容易出现抖动的问题,为实现对系统加速性能的实时控制,提出了一种基于内环前馈非线性补偿器和外环由位置微分速度、加速度反馈相结合的控制策略,解决了大惯量系统控制不稳定性问题,该方法具有重要的工程应用价值。

[1] 肖前进,贾宏光,章家保,等. 电动舵机伺服系统非线性辨识及补偿[J].光学精密工程,2013,21(8)：2038-2042.

[2] 张新华,杨瑞峰. 含间隙的电动伺服机构非线性振荡研究[C]//第五届全国振动利用工程学术会议暨第四次全国超声电机技术研讨会,2012：825-828.

[3] 刘强,尔联洁,刘金琨.摩擦非线性环节的特性、建模与控制补偿综述[J].系统工程与电子技术,2002,24(11)：45-52.

[4] 刘丽兰,刘宏昭,吴子英,等.考虑摩擦和间隙影响的机床进给伺服系统建模与分析[J].农业机械学报,2012,41(11)：212-218.

[5] 陆豪,李运华,田胜利,等. 驱动大惯量低刚度负载的推力矢量控制电动伺服机构的μ综合鲁棒控制[J].机械工程学报,2011,47(2)：180-188.

[6] Tao G,Kokotovic P V. Adaptive control of systems with backlash[J].Automatic,1993,29( 2) : 323-335.

[7] Shin W H,Lee I,Shin Y S,et al. Nonlinear aeroelastic analysis for a control fin with an actuator[J].Journal of Aircraft,2007,44(2): 597- 605.

[8] 姚郁,杨有为,马杰. 仿真转台控制系统μ综合应用研究[J].电机与控制学报,2005,9(5)：456-460.

[9] 史建伟,史永丽. 基于自抗扰控制的伺服系统输出间隙补偿研究[J].电力学报,2009,24(2)：105-108.

[10] 李朝富.提高电动舵机动态特性的方法研究[J].战术导弹控制技术,2008,30(2) : 37-40.

[11] 黄立梅,吴成富,马松辉. 制飞控系统舵机间隙影响的非线性补偿器设计[J].飞行力学,2012,30(2)：133-135.

[12] 李友年,陈星阳.舵机间隙环节对控制系统的影响分析[J].航空兵器,2012,12(1)：25-33.

Research on Nonlinear Factor Characteristics and Control Method on Large Inertia Electromechanical Actuator Servo Mechanism

ZHANG Xin-hua, HUANG Jian, ZHANG Zhao-kai, DUAN Xiao-shuai, LIU Yuan

(Beijing Institute of Automatic Control Equipment, Beijing 100074, China)

For flight attitude control problem affected by nonlinear property of hypersonic vehicle, the influences of nonlinear factors which are driving space, stiffness, friction torque in the electric servo mechanism are analyzed in this paper, and the definition and generation conditions of limit cycle caused by the backlash are also discussed. For the problems of limit cycle oscillation and the airfoil intensified oscillation with large inertia caused by driving space, a system backlash limit cycle gap model and nonlinear vibration model are established, and the backlash compensator methods are proposed. This paper focuses on the influence of backlash, airfoil moment of inertia, servo stiffness and disturbing force to servo mechanism system. Based on increasing backlash compensator by controlling inner ring, the design method of accelerated negative feedback is introduced to the outer ring, solving jitter problem in large inertia system, and the simulation and experimental results demonstrate that this theory is correct.

Electromechanical；Limit cycle; Clearances ; Stiffness；Nonlinear oscillations

2016-11-12；

2016-12-08

国家自然科学青年基金(61603051)

张新华(1972-),男,博士,研究员,主要从事伺服控制方面的研究。E-mail：sloht0033@126.com

10.19306/j.cnki.2095-8110.2017.02.008

U666.12

A

2095-8110(2017)02-0031-07