多层离散小波变换系数的稀疏向量构造的改进*

罗文东,田慕阳,张 萌

(东南大学电子工程学院,南京 210096)

多层离散小波变换系数的稀疏向量构造的改进*

罗文东,田慕阳,张 萌*

(东南大学电子工程学院,南京 210096)

融合离散小波变换和压缩感知的图像压缩方案很好避免了采用离散余弦变换和压缩感知时所带来的块效应,但当前基于单层离散小波变换的算法压缩比较低,基于多层离散小波变换的算法重构质量不佳。为了解决这些不足,根据离散小波变换系数的特点,对现有基于多层离散小波变换的算法提出了改进。图像经小波变换后,保留图像最高层低频系数,高频系数的构造方式给予适当改进。实验结果表明,与现有算法相比,重构图像的峰值信噪比PSNR(Peak Signal to Noise Ratio)值得到2 dB～4 dB提高。

图像压缩;压缩感知;离散小波变换;稀疏向量

根据奈奎斯特采样定理,传统的信号采样速率必须大于或等于被采样信号带宽的2倍,才能无失真地恢复模拟信号。当前信息需求量急剧增加,这种高速采样的过程浪费了大量的资源。近年来,压缩感知CS(Compressed Sensing)的出现突破了这一限制。压缩感知理论使得信号采集的同时对数据进行压缩,即感知压缩了的信息。其核心思想是如果信号是可压缩的或者在某个变换基上是稀疏的,那么就可以利用观测矩阵将其投影到一个低维空间,获得远小于信号维度的测量值,再通过压缩感知重构算法求解出原始信号[1]。压缩感知的出现,给信号处理领域带来了解决问题的新思路。

压缩感知理论广泛应用于图像压缩处理中,但自然界的大部分信号并不都是稀疏的,使用压缩感知的前提条件就是图像是稀疏的,所以稀疏向量的构造对整个图像的压缩重构质量起决定性的作用。幸运的是大部分自然信号,例如图像、视频和语音信号等,都能在特定的正交变换基上进行稀疏表示。对于图像和视频信号而言,典型的稀疏基包括离散余弦变换基、离散小波变换基等。离散余弦变换给图像带来明显的块效应[2],离散小波变换可以克服这个缺点,而且离散小波变换还可以进行多层变换,使用起来更灵活。本文以多层离散小波变换为基础,对稀疏向量构造算法存在不足提出了改进,改进后的算法能够提升图像的重构质量。

1 离散小波变换系数的稀疏向量研究

1.1 压缩感知简介

设x∈RN×1为一维信号,则其可以由一组正交基展开(例如小波基)Ψ={ψ1,ψ2,…,ψN},即

(1)

其中,yk=〈x,ψk〉。当信号x在某个基Ψ上仅有K≪N个非零系数yk时,称Ψ为信号x的稀疏基。

一般来说,信号经过某种变换(如离散小波变换)之后,其系数可以认为是稀疏的。例如,对信号进行小波变换之后,可以通过保留其系数中的K个较大的分量,而把其他N-K个分量置零(因为这N-K个变换域系数对信号重构的贡献很小)。这样,即可以认为信号x在小波基Ψ下是K稀疏的。对于信号x,可将其投影到一组测量向量Φ={φ1,φ2,…,φN}上,得到x的M个线性测量,即

s=Φx

(2)

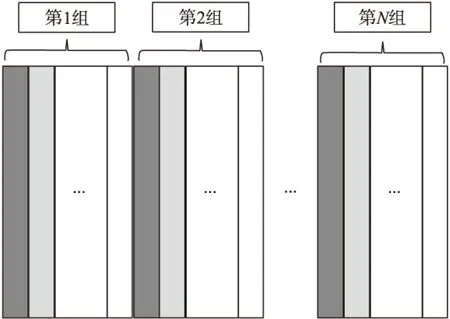
式中:Φ为M×N矩阵,由此看到,压缩感知将信号x从N维降为M维观测信号s。对于给定的测量值s从式(2)求解是一个线性规划问题。因K

(3)

Φ满足RIP,就可以由s无失真地重构出x。CS信号的重构问题可以表示成求解0范数下的最优化问题,然而求解0范数最优化是个非确定性多项式难题(NP-hard),可将问题转换为求解1最小范数下的最优化问题:

(4)

1.2 单层离散小波变换稀疏向量的构造

岑翼刚等[5]提出了基于单层离散小波变换的压缩感知算法,保留图像低频系数,只对高频系数进行测量,重构图像质量得到极大提升。Zhang Jin等[6]提出了一种行列平均的算法。单层离散小波变换后,低频部分不做处理,分别对3个子块HLl、LHl和HHl的各行测量、重构;再对3个子块的各列做测量、重构,最后求平均,重构图像。该方法克服了只对行或者列进行处理而忽略图像是二维的缺点。荣雁霞等[7]根据图像小波变换系数的特点,将图像分块思想与小波变换相结合,提出一种基于离散小波变换的分块压缩感知算法。每一个图像块经小波变换后,保留图像低频系数,只对高频系数进行观测。实验结果表明,与不分块压缩感知算法相比,重构图像的PSNR值有2 dB～4 dB的提高,重构时间明显减少。与基于二维离散余弦变换的分块压缩感知算法相比,块效应有明显的改善,重构质量明显提高。上述3种算法只做单层离散小波变换,低频系数占图像的比例还是较大,造成图像的压缩比低。

1.3 多层离散小波变换稀疏向量的构造

Mohit Kalra等[8]提出的多层离散小波变换构造稀疏向量的方法。其实是借用了SPIHT算法中的父子关系。我们知道离散小波变换第1层的3个高频系数是最稀疏的,越往上系数绝对值越大,如图1所示,这种在水平方向不同层次分别取1个、4个、16个系数的关系能很好满足多层离散小波变换构造稀疏向量的要求。

图1 Kalra稀疏向量构造算法

Mohamed Deriche和Muhammad Ali Qureshi等[9]对Mohit Kalra的算法提出了改进,把同一相对位置的水平分量,垂直分量,对角分量依次组合成新的稀疏向量(因为Mohit Kalra首先提出这种组合多层离散小波系数的算法,为叙述方便,之后我们把如图1所示的构造算法叫做Kalra构造算法)。图1以16×16图像为例,做了3层离散小波变换,最高层低频系数取a1,然后分别是水平方向21(1+4+16)个b1,垂直方向21个c1,对角方向21个d1组成一个长度为64的向量,依次取完共有4个这样的向量。该方法虽然增加了向量的长度,但是同一相对位置的水平、垂直和对角分量组合在一起容易造成绝对值大的数据的集中,构造的向量会有较多的不稀疏。

Muhammad Ali Qureshi和Mohamed Deriche等[10]原创性地提出了一种在多层离散小波变换下构造稀疏向量的方法。经过离散小波变换,该文献提出的构造稀疏矩阵的方法就是先分块,然后取出每一块相同位置的元素构成列向量(为叙述方便,之后我们把它叫做Qureshi构造算法)。如图2所示,经过了两层变换,分成了相同的16块。构造的稀疏向量也只有16个元素。3层变换的稀疏向量也只有64个元素。但是该方法构造的向量所含元素太少,会有较多向量不满足稀疏性要求。

图2 Qureshi稀疏向量构造算法

2 改进算法

为了验证我们对稀疏向量构造的改进,我们首先给出了图像压缩重构的流程图,如图3所示。

图3 图像压缩重构的流程图

具体步骤如下:

(1)原始图像经多层离散小波变换,除最高层的低频系数,其他我们可以认为基本稀疏。为了后续的压缩感知算法对稀疏性的要求,我们设定一个阈值,对于绝对值小于阈值的系数,我们直接量化为零。

(2)构造一系列的稀疏向量。采用文献Kalra或Qureshi构造算法构造一系列稀疏向量。

(3)为了便于后续的硬件实现,测量矩阵选用了满足RIP的伯努利矩阵,它只含有1和-1两种元素。稀疏向量与伯努利矩阵相乘得到了维度更小的向量,数据得到了压缩。

(4)通过OMP算法对向量进行重构,得到测量前的稀疏向量,稀疏向量重新组合后经离散小波逆变换,最后得到了重构的图像。

论文的重点放在对稀疏向量构造的改进。两种构造算法在相同离散小波变换层数时,得到的向量个数相同,每一个稀疏向量的元素个数相同,所以我们的改进算法适用于两种构造算法。改进的算法如下:

最高层的低频系数保留。保留最高层低频系数在不太影响压缩比的情况下,能提升重构质量。比如经过3层变换,最高层低频系数占整个图像的1/64,而且系数绝对值大,不利于稀疏向量的构造。

Kalra和Qureshi构造算法构造的列向量分成N组,依次提取不同组相同位置的向量组成更长的新向量。如图4所示,相同颜色的向量为不同组的相同位置。分析发现,按顺序每N个组成一个列向量,有时候会连续好几个向量的元素绝对值较大,构造的向量会不稀疏。所以用该组合的方法能够最大化打散向量,而且更长的向量有利于稀疏向量的构造。

图4 改进的组合方式

对于256×256图像,以3层离散小波变换为例,保留最高层低频系数后一共有1 024个向量,每个向量含63个元素。下面给出分组数和向量元素个数的关系。

表1 不同分组数构造的元素个数

3 仿真结果

为验证文中改进算法的性能,选取标准测试图像Lena 256×256。观测矩阵选取伯努利随机矩阵,重构算法采用OMP算法。在测量比MR(M/N)分别为0.2、0.3、0.4、0.5、0.6、0.7和0.8的情况下取得数据,画出曲线图,形成对比,如图5所示。

通过折线图我们可以看到,两种稀疏向量构造算法经改进后,PSNR都有明显的提升,总体而言,Qureshi构造算法改进后最优。为了形象表示改进后的效果,我们在MR为0.5时得到截图,如图6所示。

图5 不同构造算法重构质量折线图

图6 MR为0.5时不同算法重构图像对比 (a)是原始图像,(b)是Kalra构造算法的效果图,(c)是Kalra构造算法改进后的效果图。(d)是Qureshi构造算法的效果图,(e)是Qureshi构造算法改进后的效果图。

对比图片可明显看出改进算法对两种构造算法的提高。

同时我们还对改进后的Qureshi构造算法不同向量长度做了探究。我们取离散小波变换为3层条件下,不同向量长度取得的数据如表2所示。随着向量长度的增加,PSNR会不断增大,这是因为长向量得到稀疏向量的概率更大。

表2 不同向量长度图像重构质量

进一步对不同层数的离散小波变换对重构质量的影响进行了探究。控制向量元素为252个条件下,不同层数离散小波变换结果如表3所示。

表3 不同小波变换层数图像重构质量

可以看出,越高层的小波变换系数绝对值越大,构成的向量也越不稀疏。

4 结语

与传统稀疏向量构造算法相比,本文通过保留最高层的低频系数以及分组提取的方法优化了稀疏向量构造算法。通过在MATLAB平台仿真表明,在相同测量比的条件下我们可以得到更清晰的图像,充分证明了改进的稀疏向量构造算法优于Kalra和Qureshi构造算法。同时我们还对不同长度的向量、不同层数小波变换对重构质量的影响进行了探究,得出的数据有一定的参考价值。

[1] 任越美,张艳宁,李映. 压缩感知及其图像处理应用研究进展与展望[J]. 自动化学报,2014,40(8):1563-1575.

[2] Hasan K K,Ngah U K,Salleh M F M. Efficient Hardware-Based Image Compression Schemes for Wireless Sensor Networks:A Survey[J]. Wireless Personal Communications,2014,77(2):1415-1436.

[3] 崔佳鹏. 基于压缩感知的图像压缩技术研究与实现[D]. 哈尔滨:哈尔滨工业大学信息与电气工程学院,2013.

[4] 尹宏鹏,刘兆栋,柴毅,等. 压缩感知综述[J]. 控制与决策,2013,28(10):1441-1445.

[5] 岑翼刚,陈晓方,岑丽辉,等. 基于单层小波变换的压缩感知图像处理[J]. 通信学报,2010,31(8A):52-55.

[6] Zhang J,Xia L,Huang M,et al. Image Reconstruction in Compressed Sensing Based on Single-Level DWT[C]//Proc of the IEEE Workshop on Electronics,Computer and Applications(IWECA). Ottawa,IEEE,2014:941-944.

[7] 荣雁霞,邱晓晖. 基于小波变换的分块压缩感知算法[J]. 计算机技术与发展,2015,25(5):29-32.

[8] Kalra M,Ghosh D. Image Compression Using Wavelet Based Compressed Sensing And Vector Quantization[C]//Proc of the 11th International Conference on Signal Processing(ICSP). Beijing,IEEE,2012:640-645.

[9] Deriche M,Qureshi M A,Beghdadi A. An Image Compression Algorithm Using Reordered Wavelet Coefficients with Compressive Sensing[C]//Proc of the 5th International Conference on Image Processing,Theory,Tools and Applications(IPTA). Orleans,IEEE,2015:498-503.

[10] Qureshi M A,Deriche M. A New Wavelet Based Efficient Image Compression Algorithm Using Compressive Sensing[J]. Multimedia Tools and Applications,2016,75(12):6737-6754.

An Improved Reconstruction to Sparse Vector for the Coefficient of Multilayer Discrete Wavelet Transform*

LUOWendong,TIANMuyang,ZHANGMeng*

(Southeast University,Nanjing 210096,China)

The image compression scheme which combines discrete wavelet transform and compressed sensing has overcome the block effect brought by the discrete cosine transform and compressed sensing. But the algorithm based on single layer discrete wavelet transform causes the low compression ratio,and the algorithm based on multilayer discrete wavelet transform causes a poor refactoring quality. In order to solve these problems,employing the characteristics of discrete wavelet transform coefficients,the better algorithm based on multilayer scheme is proposed. After the discrete wavelet transform,reserving the low frequency coefficients at the highest level,the method to reconstruct the high frequency coefficient is appropriately improved. Compared with the existing algorithms,the experimental results of the proposed algorithm show that the PSNR(Peak Signal to Noise Ratio)of reconstructed image was improved about 2 dB～4 dB.

image compression;compressed sensing;discrete wavelet transform;sparse vector

项目来源:江苏省普通高校研究生科研创新计划项目(SJLX15_0095,SJLX16_0081);东南大学研究生教改项目(XJGKT14-01);本科教改项目(2013-033);江苏高校品牌专业建设工程项目

2016-07-28 修改日期:2016-09-25

C:6140C

10.3969/j.issn.1005-9490.2017.02.029

TN941

A

1005-9490(2017)02-0405-05