4阶Colpitts MOS管混沌电路设计*

肖 鹏,冯烨佳,李文石

(苏州大学电子信息学院,江苏 苏州 215006)

4阶Colpitts MOS管混沌电路设计*

肖 鹏,冯烨佳,李文石*

(苏州大学电子信息学院,江苏 苏州 215006)

仅增加一个线性电容并联于单电感两端,使3阶Colpitts MOS管电路成为4阶混沌电路。该电容与电感形成选频谐振子电路,便于产生混沌信号,可扩展存在混沌的参数取值范围。结合新电路归一化状态方程,分别计算电感电流和三只电容端压的4个李指数,探讨关键参数对该混沌电路的影响。对比MATLAB仿真数据与实测单MOS管电路的输出,一致性地显示4阶混沌特有的混沌吸引子已经实现。

Colpitts电路;4阶混沌;MOS;李指数;实测数据

混沌现象具有3个重要特点:初值敏感性、奇怪吸引子和长期不可预测[1]。

1975年,李天岩博士与约克教授计算认为:周期3意味着混沌[2]。

1983年,蔡少棠教授率先提出3阶最简自治混沌电路,仅有1L-2C-1D(蔡氏二极管,非线性负电阻)。通过配置合适参数,该电路方便实现周期、拟周期和混沌的3态变化[3]。

应用1只到2只运放实现的蔡氏二极管,仍嫌复杂,于是,技术发展演进到1994年,Kenndy提出三点电容反馈Colpitts混沌电路,这个双极性单管混沌电路虽以结构简洁著称,但其混沌频谱连续性仍不佳,混沌存在的参数范围仍狭窄[4];2008年禹思敏教授为电感并联电容,得到的4阶电路的优点是初步扩展了混沌参数的存在范围[5]。

调研表明,基于MOS管设计实现新的混沌电路的方法,愈加受到重视,典型的研究问题一是针对高阶混沌,二是针对超宽频谱[6]。

混沌电路设计方法学简单分类:(1)增模块法,基于经典混沌电路,少量增加储能元件或非线性元件,构成更复杂的高阶混沌电路;(2)减模块法,针对复杂的混沌电路,通过提取电路中的最小混沌单元,简化系统,判断混沌特性;(3)方程映射法,考察状态方程中包含的基本储能单元的2种可测参量(电压、电流),聚焦非线性元件特性的分段近似电路表达,做混沌判断;(4)三框图法,基于两个独立频率信号产生电路和一个开关模块,化简,持续做混沌判断。

受到文献[5]的启发,本工作的想法是通过最小化地增加电路复杂度,仅增加1只电容,将3阶MOS管Clopitts混沌电路改造为4阶,期间重视归一化方程分析、李指数计算与混沌判断,对比给出实际电路的实测相图。区别于文献[7]中的3阶,本工作的创新点是利用MOS器件结合增加的单电容,产生4阶单涡卷混沌信号;研究的工程意义可以加速有源电感Colpitts MOS管混沌电路的芯片集成。

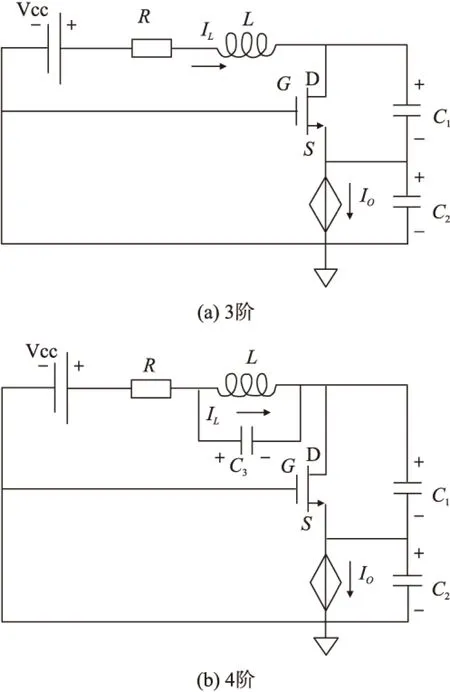
图1 Clopitts MOS管混沌电路

1 构建新拓扑

新的4阶混沌电路的组合设计就从观察图1(a)获得灵感[5,7]。

图1(a)是经典的三点式Colpitts混沌电路[8],结构简单,电压源和电流源恒定,MOS管起非线性放大作用,通过设置电路元件的合适参数,将使电路遍历周期、拟周期和混沌这3态。之所以选择NMOS管,是因为相对于PMOS管,载流子迁移率高,版图面积节省。

图1(b)中类似文献[5]的贡献,特别加入电容C3,并联在电感L两端,LC3形成选频谐振网络,旨在增加混沌区间的范围,使电路更易产生混沌。本文尝试的基本假设:以最少增加结构复杂性为代价,换取新的感兴趣性能,例如改变原有混沌电路吸引子形状,产生一个4阶混沌新电路。

2 状态方程和无量纲化

列写图1(b)所示电路的状态方程,为之后在相空间计算李指数作铺垫。其中,引用了式(1)、式(4)和式(5)[8-9],其余公式均是我们根据4阶Colpitts混沌电路推导得到。

MOS管的伏安关系表达式为Id=f(VGS,VDS),如下简化处理之。

假设:不考虑沟道效应、体效应以及其他二级以上效应;NMOS工作的可能典型理想区域是饱和区、线性区或截止区。

漏极电流Id与栅源电压VGS和漏源电压VDS的关系:

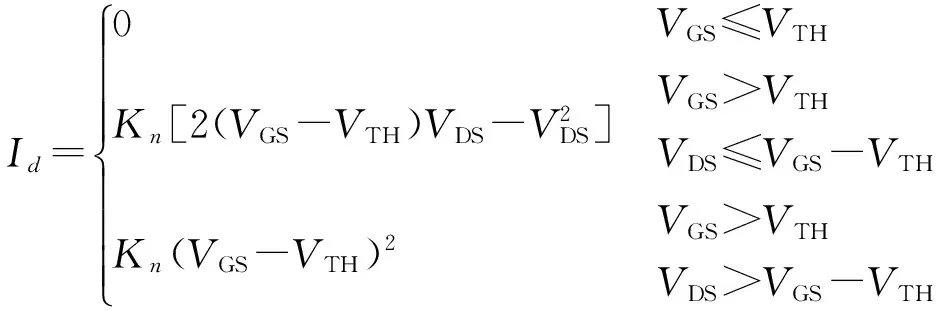
(1)

上式Kn=μnCoxW/2L。结合图1(b)为式(1)换元(令VGS=-VC2,VDS=VC1),得:

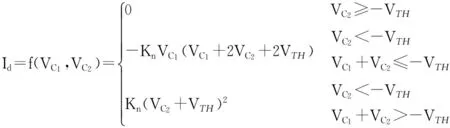
(2)

列写图1(b)的电路模型的状态方程:

(3)

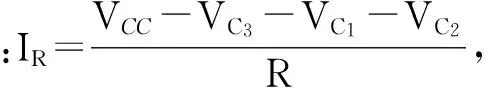
变量代换约定:引用式(4)和式(5);特别构造式(6)和式(7)如下:

(4)

(5)

(6)

IL=kw′

(7)

按照上述变换规则,修整式(3),有:

(8)

式中,非线性函数:

(9)

分析式(8)的平衡点,即令式(8)中的方程①②③④各自等于0。

至此,一个可能产生混沌的系统方程已经确立,包括式(8)和式(9)的第3条件项。

若想实现混沌,则系统要在平衡点处实现不稳定,即位于平衡点处的雅各比矩阵的特征值,需出现混沌奇异吸引子。

考察平衡点:式(9)描述的平衡点有且仅有一个,

(10)

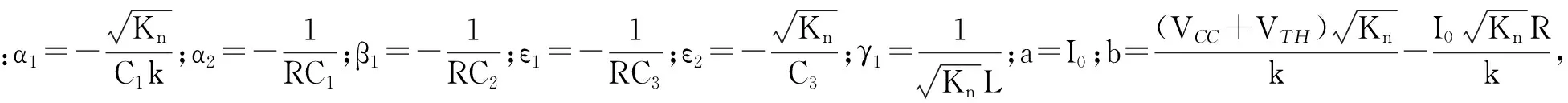
(11)

上述9个参变量均用于控制系统混沌与否。其中,容易理解的α2、β1和ε2相当于频率量,参数k是相图的比例缩放系数,再如参数a代表电流源的数值,该参数直接影响VC1与VC2充放电速度,也加速波形的收敛稳定。

综上,若要出现混沌,则状态方程中的非线性函数有且仅有一种形式满足条件式(11)的第3条件项。

3 李指数计算与混沌判断

确定产生混沌的9个参变量的方法:基于蒙特卡罗方法的提示,总共仿真150次,找到了一组优值,其满足由李指数做出的混沌判据。

设置(10)中的系数分别为:a=0.7,k=1,b=2,α1=-2.2,α2=-4.5,β1=-0.95,ε1=-3,ε2=-1.2,γ1=2.1,则可得相图:图2和图3(x=Vc1,y=Vc2,z=Vc3,w=iL)。

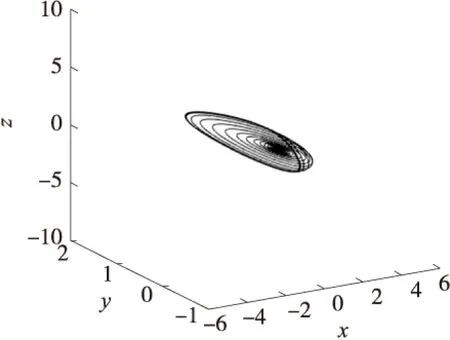
图2 x-y-z相图

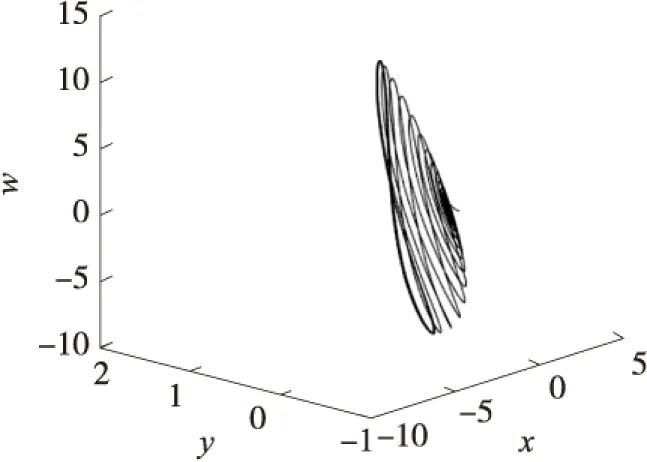
图3 x-y-w相图

此时位于平衡点(0,0,0,0)的雅各比矩阵的特征值为:

-7.8358;-0.6843+1.3298i;-0.6843-1.3298i;0.7543

根据4个特征值可知,该平衡点为指标1的鞍点,由此可知本设计的混沌电路已初步达标。为验明该系统产生了混沌信号,还需理论计算并判断李雅普诺夫指数的正负,以便整体把握该系统的混沌拓扑吸引子,所得李指数图形参如图4所示。

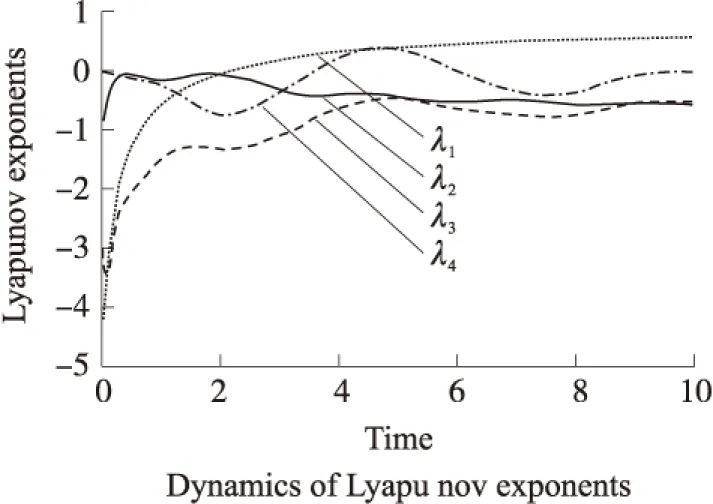
图4 系统李指数的检测情况

图4中发现在系统运行的末端,存在一个大于0的李指数λ1(lambda1),存在一个接近0的李指数λ2(lambda4),还有两个小于0的李指数λ3和λ4。

式中:λ1可保证系统存在发散性,即相空间会出现曲线发散,相互远离;

λ2可保证系统做永不停息的运动,相空间表现为曲线永不闭合;

λ3与λ4的绝对值之和大于λ1,这样可保证系统运动处于一个有界封闭空间。

综上分析,系统处于一个有界的空间内,做永不停止的拉伸、折叠运动,如此,一个混沌系统即已构成。

为进一步分析系统与关键参数值的敏感程度,这里在仅改变一个参数的情况下(例如改变ε2,维持其他参数不变),试图通过该唯一参变量描述系统进入混沌的条件,实验结果参见图5所示。

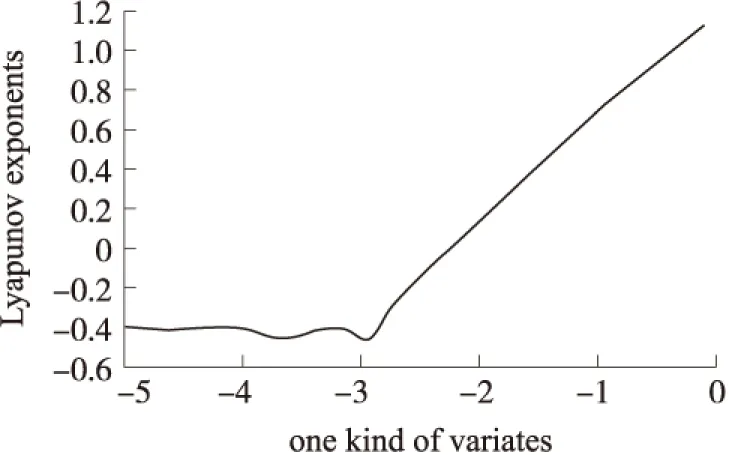
图5 ε2与系统最大李指数的关系

图5显示:在ε2约小于-2.3时,系统处于收缩状态,没有混沌特有的吸引子结构,但是当ε2约大于-2时,系统的最大李指数明显大于零,系统进入了混沌状态。这说明仅仅通过微小地改变一个参数值大小,就能使该新电路加速进入混沌。

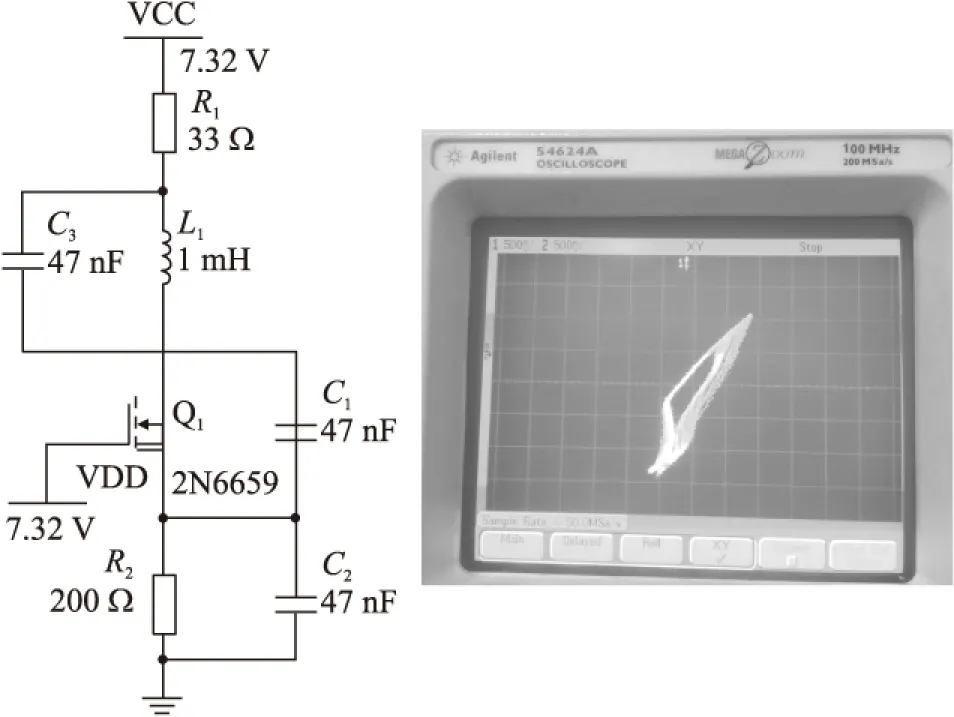
图6 实际电路结构与VC1-VC2相图实测图像

4 实际电路的实测相图

如图6所示,图左总共7个元器件,电源和栅偏共用7.32V直流供电,内部恒流源由R2支路近似;实测结果照片示于图右,对比图6和图2图3中的x-y相图,趋势一致。

实际结果与仿真结果,存有误差,主要原因有以下的3点:(1)计算过程会引入误差,例如实际电感有内阻,这点在建立系统方程时没有考虑到;(2)实际电阻电容元件含有标称值误差;(3)为使电路简洁,利用(VC2/R2)近似代替了Io独立电流源,这引入了误差。

5 结论与讨论

本文基于一个3阶MOS管Clopitts混沌电路,通过增加一个线性电容成功地实现了一个具有选频特性的4阶MOS管Clopitts混沌电路。

相较之前的3阶Clopitts混沌电路,总结本电路优势如下:

(1)应用增模块设计方法,通过并联谐振网络,致使新电路在参数选取后更易进入混沌振荡(例如能敏感于单参量);

(2)简化处理MOS管的伏安关系表达式Id=f(VGS,VDS),关键有3,一是列写基本方程包括分段描述,二是表达电路参数的换元,三是标度变换本质是从国际单位制约束下的电路图参数集合域,映射进入因能量有限导致的参数有界的相图坐标系中;

(3)无量纲化系数的选取参见文献[5],计算李指数,大于0是混沌判据,同时计算演示了单参数扰动之于混沌的贡献;

(4)仿真结果参见图2和图3,对比近似电路的实测结果演示如图6所示,证明了电路关键储能元件端压之间的相图,其所呈现的“梨形”,趋势一致。

未来电路设计的趋势是超低功耗,而实现该目标最直接的方式为降低供电电压[10-11]。降低电压有两种思路:(1)采用更先进工艺(例如28nm);(2)工作在近零阈值区[12]。前者成本太贵,不适合推广使用;后者MOS管的漏流危险提升,工作区域伏安特性复杂,特别是高阶负效应影响明显。待这些问题解决后,超低功耗的混沌信号产生芯片一定大放异彩,尤其在无电感混沌电路方向[13]。

[1] Lorenz E N. Deterministic Nonperiodic Flow[J]. Journal of the Atmospheric Sciences,1963,20(2):130-141.

[2] Li T Y,Yorke J A. Period Three Implies Chaos[J]. The American Mathematical Monthly,1975,82(10):985-992.

[3] Chua L O,Yu J,Yu Y. Negative Resistance Devices[J]. International Journal of Circuit Theory and Applications,1983,11(2):161-186.

[4] Kennedy M P. Chaos in the Colpitts Oscillator[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,1994,41(11):771-774.

[5] 禹思敏. 四阶Colpitts混沌振荡器[J]. 物理学报,2008,57(6):3374-3379.

[6] Izrailev F M. Simple Models of Quantum Chaos:Spectrum and Eigenfunctions[J]. Physics Reports,1990,196(5/6):299-392.

[7] 王春华,徐浩,万钊,胡燕. 基于金属氧化物半导体晶体管Colpitts混沌振荡电路及其同步研究[J]. 物理学报,2013,62(20):208401-1-8.

[8] 拉扎维. 模拟CMOS集成电路设计[M]. 西安:西安交通大学出版社,2003:732-746.

[9] 徐浩. 蔡氏多涡卷电路和Colpitts混沌电路的研究与设计[D]. 湖南大学,2013.

[10] Trejo-Guerra R,Tlelo-Cuautle E,Carbajal-Gómez V H,et al. A Survey on the Integrated Design of Chaotic Oscillators[J]. Applied Mathematics and Computation,2013,219:5113-5122.

[11] Halter J P,Najm F N. A Gate-Level Leakage Power Reduction Method for Ultra-Low-Power CMOS Circuits[C]//Proceedings of the IEEE Custom Integrated Circuits Conference,1997:475-478.

[12] 王会杰,王春华,何海珍,等. 一种基于MOS亚阈值特性的低功耗电压基准源[J]. 微电子学,2011,41(5):654-657.

[13] 郭燕,贾华宇. 基于CCⅡ的集成混沌振荡器设计[J]. 电子器件,2015,38(5):1064-1069.

Four Order Colpitts MOS Chaotic Circuit Design*

XIAOPeng,FENGYejia,LIWenshi*

(College of Electronic Information,Suzhou University,Suzhou Jiangsu 215006,China)

To change classical 3 order Colpitts MOS oscillator into 4 order chaotic circuit by adding one capacitance in parallel of an old inductance. The built frequency-selected net brings new advantages which is easy to generate chaotic signals and to extend the range of parameters on chaos being. Combining our new circuit’s equations,total four Lyapunov exponents are computed for the current of inductance and the voltages of three capacitors. Then we explore the influences between this circuit and its key parameter sets. Our simulation results in MATLAB show the same pear-shaped phase-charts or attractors compared with the tested data from 2N6659 type-MOS four order chaotic circuit by Oscillator of Agilent 5462 A.

Colpitts circuit;4 order chaos;MOS;Lyapunov exponents;tested data

项目来源:江苏省2015年度普通高校研究生科研创新计划项目(省立校助)(KYLX15_1244);2014年江苏省自然科学基金项目(BK20141196)

2016-03-28 修改日期:2016-06-13

C:1230B

10.3969/j.issn.1005-9490.2017.02.015

TN710

A

1005-9490(2017)02-0337-05