六轮铰接式电动轮自卸车差速控制策略及仿真*
姜立标 丘华川 凌诗韵 何家寿
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
六轮铰接式电动轮自卸车差速控制策略及仿真*
姜立标 丘华川 凌诗韵 何家寿
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
现有的六轮铰接式电动轮自卸车差速控制策略只是简单地实现差速,且其忽略整车横摆控制和驱动防滑控制而导致整车动力学性能较差.为此,提出了基于驱动力分层控制的差速控制策略.首先基于拉格朗日方程法推导了包含整车纵向、侧向、横摆及前车身侧倾自由度的整车动力学数学模型,然后设计由总驱动功率及横摆控制功率决策层、差动驱动分配层和驱动防滑稳定层组成的分层控制差速控制策略.文中运用自抗扰控制算法计算出纠正转向角偏差所需的横摆控制功率,采用最优滑移率识别算法对各轮驱动功率进行修正.离线仿真结果表明,所提差速控制策略在不同工况和路面下均能很好地实现各轮差速,同时保证了较好的整车转向性能和各轮工作的稳定性能.
铰接式自卸车;电动轮;差速控制策略;分层控制;自抗扰控制;离线仿真
六轮铰接式电动轮自卸车前后车架通过铰接装置连接左、右两侧安装有转向液压油缸和全液压转向系统使其形成一定的折转角来实现转向,以获得较小的转弯半径及高度灵活的机动性能[1].前后车架还可以在垂直于公共纵向轴线的平面上做无限制的转动,使前、后车轮都能够充分接触到地面,在降低前、后车架扭转刚度的同时保证良好的通过性[2]. 采用电传动和电动轮驱动技术,六轮驱动具有独立、精准、实时可控的优点,在节能减排、结构布置、整车动力学等方面都有着传统动力驱动自卸车无可比拟的优越性[3].
然而,六轮铰接式电动轮自卸车各轮独立驱动在拥有更多控制自由度的同时,也带来了差速控制问题[4].只有精确控制好各电动轮驱动力矩和转速,实现不同工况下各轮协调工作,才能充分发挥其多自由度控制的优势.目前主要有等转矩控制[5- 6]和等滑移率控制[7-8]两种差速控制策略,但两者都只是简单地实现差速,且由于忽略了整车横摆控制和驱动防滑控制,各轮驱动与转向系统工作不协调导致整车动力学性能较差.
为解决该问题,文中从整车控制层面出发,建立了整车动力学数学模型,提出了基于驱动力分层控制的差速控制策略,将横摆控制、差速控制和驱动防滑控制整合到其中,以实现不同工况下六轮的协调工作,并进行了离线仿真实验.
1 整车数学建模
首先进行以下假设:①自卸车行驶在平坦路面,路面垂向不平度输入为0;②前悬架工作在线性区间,刚度、阻尼为恒定值;③忽略轮胎回正力矩的影响,只考虑纵向力和侧向力;④忽略空气阻力;⑤包含前悬架在内的整车结构都是刚性的;⑥只考虑轮胎与路面之间的摩擦力,其他摩擦力为0[9-10].
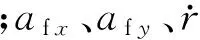
为了使动力学模型更加符合实车情况,文中建立的整车动力学模型包括前车的纵向运动、侧向运动、横摆运动和侧倾运动4个自由度,后车的纵向运动、侧向运动和横摆运动3个自由度以及6个车轮的转动自由度共13个自由度.取整车状态变量为X=[ufvfrfrrφ]T,应用拉格朗日方程法,整车的状态方程可推导为
(1)
式中:
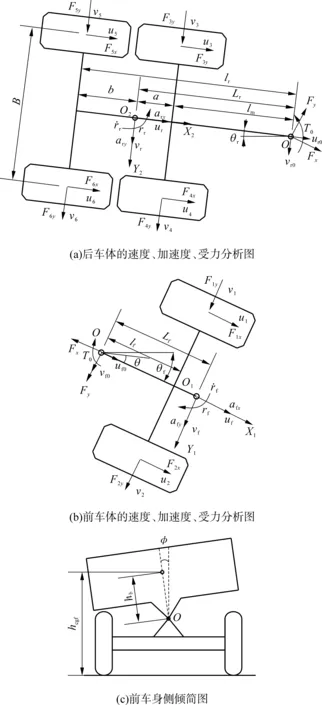
图1 前、后车体的速度、加速度、受力分析图及前车身侧倾简图
Fig.1 Velocity, acceleration and force of the front and rear truck body and roll diagram of the front body

(Kφ-mbfghb)φ-mbfhbufrf+m1hjrfuf]T;
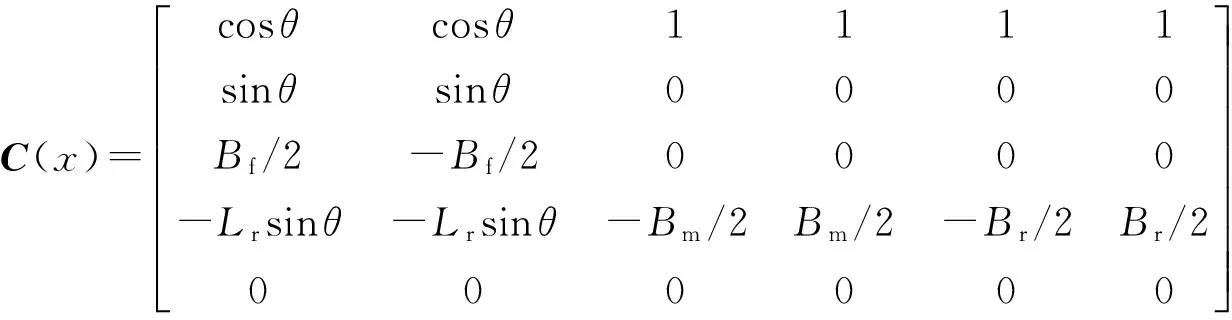

m=mf+mbf+mr,m1=mf+mbf,M=mbfhb(2rf+rr),mf为前车非簧载质量,mbf为前车簧载质量,mr为后车质量,Izzf为前车非簧载质量横摆转动惯量,Izzr为后车质量横摆转动惯量,I33、I13分别为前车身质心处的横摆转动惯量和侧倾横摆转动惯量积,Kφ、Cφ分别为前悬架侧倾刚度系数和阻尼系数,g为重力加速度.
接着建立Gim理论轮胎模型[11-12]、全液压转向系统模型及轮胎法向载荷计算模型、轮胎动坐标速度计算模型、轮胎侧偏角计算模型、车轮旋转动力学模型、路面输入等相关辅助计算模型,最后基于Matlab/Simulink软件搭建成整车离线仿真模型.
2 基于分层控制的差速控制策略
2.1 分层控制差速策略的总体设计方案
文中设计的分层控制差速策略主要由总驱动功率及横摆控制功率决策层(简称决策层)、差动驱动分配层(简称分配层)和驱动防滑稳定层(简称稳定层)组成,总体控制框图如图2所示.
决策层根据油门踏板的位置Acc及设定的驾驶感受计算出总驱动功率PD;根据驾驶员转向指令δ以及“人-车-路”状态观测器采集的前、后车体的实际转向角θ,经自抗扰控制得到所需的横摆控制功率ΔPd.分配层根据“人-车-路”状态观测器采集的各轮法向载荷Fzi,同时考虑各轮边电机额定功率PN的限制,将总驱动功率PD和所需的横摆控制功率ΔPd按照差动驱动的方法分配给各轮,得到各轮目标驱动功率Pd1、Pd2、Pd3、Pd4、Pd5、Pd6. 稳定层根据“人-车-路”状态观测器采集的各轮转动角速度ωi和纵向速度uωi判断各轮工作状态处在附着稳定区还是非稳定区,对各轮目标驱动功率进行修正,得到各轮最终驱动功率P1、P2、P3、P4、P5、P6,输入给轮边电机驱动系统得到各轮驱动转矩T1、T2、T3、T4、T5、T6,并输入到整车动力学模型.
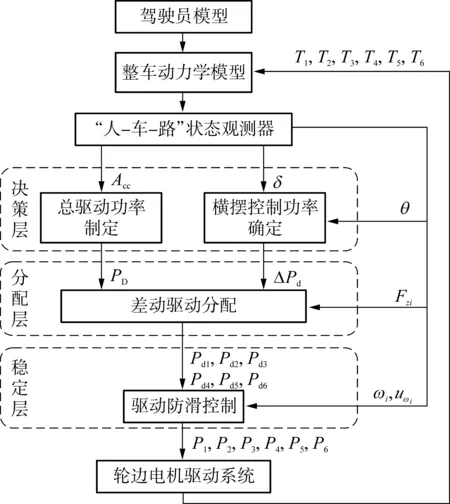
图2 驱动力分层控制的差速控制策略总体框图
Fig.2Overallblockdiagramofdifferentialcontrolstrategybasedondrivingforcehierarchicalcontrol
2.2 总驱动功率及横摆控制功率决策层
文中采用舒适型驾驶风格,总驱动功率与油门踏板位置成线性关系,总驱动功率为
PD=AccP
(2)
式中,P为整车额定功率.
文中以整车转向角为横摆控制变量,实时监测其实际值θ与目标值δ的偏差值,通过自抗扰控制算法计算出纠正该偏差所需横摆控制功率ΔPd,并将其合理分配给各电动轮,从而形成一个与转向方向相同的横摆力矩,提高转向的速度和精度,改善整车动力学性能.另外,在转向角达到目标值附近、转向驱动力矩输出为0时,可通过调整该横摆力矩的方向对前、后车体转向角进行微调,将实际转向角与目标值的差值稳定在阈值之内,降低转向系统的动作次数.
自抗扰控制算法主要由安排过渡过程(TD)、扩张状态观测器(ESO)、非线性控制律(NCL)组成[13-15],如图3所示.它能快速无超调地跟踪目标值,并且不要求被控对象具有精确的数学模型.
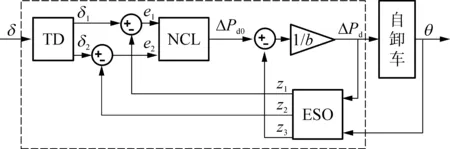
图3 自抗扰控制原理
安排过渡过程子模块根据转向目标值δ给出其安排过渡过程值δ1并提取出其微分信号值δ2:
(3)
式中,r1、h为可调参数,fhan(δ1-δ,δ2,r1,h)为最速控制综合函数[12].
扩张状态观测器子模块根据所需横摆控制功率ΔPd和实际转向角θ,估计出状态值z1、z2以及总扰动值z3.
(4)
式中,β1、β2、β3、b为可调参数,fal(e,,h)为非线性组合函数[13].
非线性控制律子模块根据转向角偏差值e1、偏差值变化率e2及扰动估计补偿值z3来确定所需横摆控制功率ΔPd:
(5)
式中,r2、h2为可调参数.
当采样步长h一定时,自抗扰控制器的参数除了反馈因子b外,其他参数的取值为[14]:r1=10-4h-2,r2=2-1h-2,β1=h-1,β2=3-1h-2,β3=32-1h-3,h2=5h.
2.3 差动驱动分配层
为了尽可能防止车轮滑移,首先将总驱动功率PD按轴荷进行分配,各轮的功率为
(6)
为了尽可能利用地面附着系数,在差动分配前首先将ΔPd按轴荷进行轴间分配,得到前轴、中轴、后轴所需的横摆控制功率:
(7)
为了简化控制算法,采用一侧增加驱动功率而另一侧减少相同驱动功率的分配方法,通过内、外侧驱动轮产生不同的驱动力形成所需的横摆力矩.当δ-θ≥0时,实际转向角比目标转向角要小,对前轴外侧轮增加功率,而对内侧轮减少功率,使前车体形成朝目标转向角方向的横摆力矩;对中轴和后轴的外侧轮减少功率,而对内侧轮增加功率,使后车体形成与前车体反方向的横摆力矩.当δ-θ<0时,所有车轮的功率变化方向相反.考虑到轮边电机额定功率PN的限制,以前轴左、右轮为例,其差动驱动分配算法如下:
若ΔPdf≥0,则
否则
2.4 驱动防滑稳定层
设s0为峰值附着系数μ0对应的滑移率,即最优滑移率.根据轮胎特性可知,当s≤s0时,dμ/ds>0,附着系数μ随着滑移率s的增加而增加,车轮没有滑转,处于附着稳定区;当s>s0时,dμ/ds<0,μ随着s的增加而减小,车轮出现滑转,处于非稳定区.附着系数的变化率dμ/ds可以表示为
(8)

(9)
式中,Td为车轮驱动力矩,Iw为车轮转动惯量.
驱动防滑控制的流程如下:根据每个车轮的工作状态单独进行控制,以车轮工作在稳定区为控制目标,如果车轮工作在非稳定区,则将实际滑移率与最优滑移率的偏差输入PID控制器,计算出该轮防滑控制所需的功率ΔPi;如果车轮工作在稳定区,则不需要施加防滑控制.
将差动驱动分配的功率Pdi减去驱动防滑控制所需的功率ΔPi,得到各轮最终输出的功率Pi:
Pi=Pdi-ΔPi
(10)
3 离线仿真实验
整车参数为:mf=5 799kg,mr=86 494kg,mbf=8 967kg,Bf=Bm=Br=3.184m,Lf=2.09m,Lr=3.27m,lf=1.6m,lm=2.5m,lr=4.5m,hb=1.632m,hj=1.186m,hcgf=2.5m,hcgr=2.0m,a=0.77m,b=1.23m,Ixzb=681kg·m2,Izzf=13 836kg·m2,Izzr=92 812kg·m2,Kφ=5×105N/m,Cφ=4.4×105N·s/m,g=9.8m/s2,rd=0.92m,Cx=7.2×105N/m,Cy=5.4×105N/m,mw=430kg,Iw=190kg·m2,PN=90kW,P=522kW.
由于转向加速工况可以同时考验自卸车的差速控制性能及整车的动力学性能,其仿真结果可以充分表征差速控制系统与全液压转向系统是否处于协调工作状态.为此,首先在满载高附着和满载低附着两种极端状态下对转向加速工况进行仿真.仿真条件为:整车满载分别行驶在高附着(峰值附着系数为0.8,滑移附着系数为0.6)和低附着(峰值附着系数为0.1,滑移附着系数为0.07)两种路面,初始车速为2m/s,转向角在第1秒到第2秒内从0°线性增加到20°并保持至仿真结束,加速踏板位置一直为1,仿真时长为5s.
为了更好地综合评价该差速控制策略的控制性能,文中主要选择以下三大性能评价指标:
(1)各轮的差速控制性能;
(2)整车转向性能,即实际转向角能否快速精准地跟随目标值,是否有震荡;
(3)各轮的稳定性,即车轮工作在稳定区还是非稳定区,是否出现打滑现象.
高附着路面转向加速工况仿真结果如图4所示.从图中可知:在驱动力分层控制作用下,实际转向角能够紧紧跟随着自抗扰控制器安排的过渡过程值,并且实际值与目标值的偏差基本处在转向阈值之内,说明转向角恒定以后基本不需全液压转向系统介入调整,保证了良好的整车转向性能;在直线行驶阶段,各轮纵向速度几乎重合,但在施加转向以后,外侧车轮的纵向速度都比内侧车轮的大,并且在转向角恒定时曲线较平滑、无振荡,说明在驱动力分层控制下各轮具有良好的差速控制性能;由于是全油门加速行驶,故各轮滑移率在仿真开始瞬间偏高,但在其他时刻大致保持在0.2以内,各轮均工作在附着稳定区,稳定性能良好.综上可知,整车在高附着路面的差速性能、转向性能和各车轮的稳定性能较好,初步验证了文中所提差速控制策略的可行性.
低附着路面转向加速工况仿真结果如图5所示.从图中可知:由于附着系数较低,在直线加速阶段,后车体4个车轮的滑移率较高,处于非稳定状态,从而导致实际转向角偏离了过渡过程值并发生了一次往复震荡,但在驱动防滑稳定层的控制下,各轮滑移率迅速减小并回归到稳定状态以保证各轮工作的稳定性;实际转向角经过一次较大范围的震荡后也很快地稳定在目标值,具有较好的整车转向性能;在转向角恒定以后,同侧车轮的纵向速度曲线基本重合在一起,各轮仍然能够处于良好的差速状态,差速控制性能较好.以上分析进一步验证了文中所提差速控制策略的可行性.
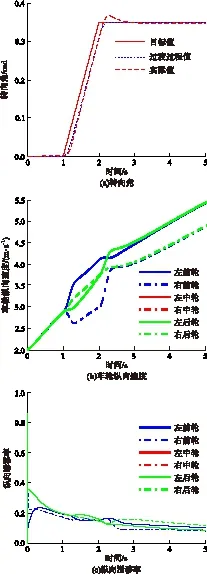
图4 高附着路面转向加速工况仿真结果
Fig.4 Simulation results of steering accelerating condition on high adhesion road
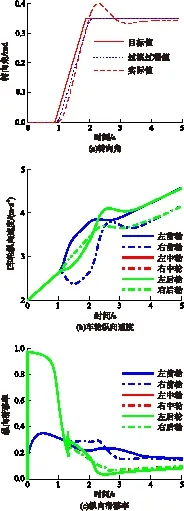
图5 低附着路面转向加速工况仿真结果
Fig.5 Simulation results of steering accelerating condition on low adhesion road
以上仿真分析只是验证了该差速控制策略在转向加速工况下的可行性,但铰接式自卸车在直线工况下的稳定性通常较差.因此,需要在直线加速工况下验证该差速策略的控制效果.令整车满载行驶在分离路面,其中左侧车轮处于高附着路面,右侧车轮处于低附着路面,初始车速为2 m/s,转向角输入为0,加速踏板位置一直为1,仿真时长为5 s,其仿真结果如图6所示.从图中可知:在该差速策略控制下,整车的实际转向角仅有极为细微的震荡,整车能够很好地保持直线行驶,不会因为左、右两侧附着系数的不同而出现跑偏现象,具有较好的转向性能;6个轮的纵向速度曲线重合在一起,说明各轮的速度值相等,各轮处于良好的差速状态.由于右侧轮均处于低附着路面,因此右前轮在仿真开始时处于一定的滑转状态,但在驱动防滑稳定层作用下,其滑移率也逐渐得到控制并保持在稳定状态,保证了各轮工作的稳定性.以上分析说明了文中所提差速控制策略在分离路面直线运动工况下的可行性.
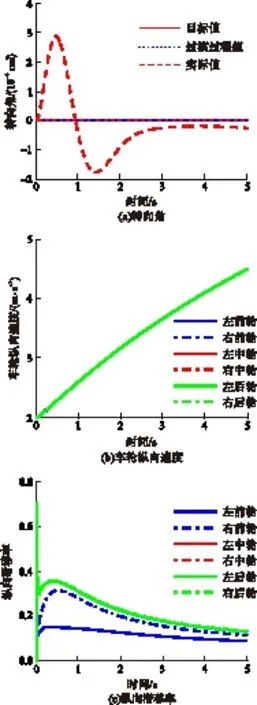
图6 分离路面直线加速工况仿真结果
Fig.6 Simulation results of linear accelerating condition on split cohesion coefficient road
4 结论
文中主要针对六轮铰接式电动轮自卸车的差速控制策略进行研究,基于拉格朗日方程法推导了包含整车纵向、侧向、横摆及前车身侧倾自由度的整车动力学模型,从整车控制层面出发设计了由总驱动功率及横摆控制功率决策层、差动驱动分配层和驱动防滑稳定层组成的驱动力分层控制差速控制策略,其中决策层基于线性驾驶风格来确定总驱动功率,运用自抗扰控制算法来计算出纠正转向角偏差所需的横摆控制功率;分配层将总驱动功率按轴荷进行分配,将所需的横摆控制功率进行差动驱动分配;稳定层设计的车轮工作状态及最优滑移率识别算法对各轮驱动功率进行修正.离线仿真结果表明,文中所提差速控制策略在不同工况和路面下均能很好地实现各轮差速,同时保证了较好的整车转向性能和各轮工作的稳定性能.
[1] JIN Chun,LIU Tong,SHEN Yan-hua.State estimation of the electric drive articulated dump truck based on UKF [J]. Journal of Harbin Institute of Technology,2015,22(6):21-30.
[2] MOON K H,LEE S H,CHANG S,et al.Method for control of steering angles for articulated vehicles using virtual ri-gid axles [J].International Journal of Automotive Technology,2009,10(4):441- 449.
[3] HAGGAG S,ALSTROM D,CETINKUNT S,et al.Mode-ling,controland validation of an electro-hydraulic steer-by-wire system for articulated vehicle applications [J]. IEEE/ASME Transactions on Mechatronics,2005,10(6):688- 692.[4] AZAD N L,KHAJEPOUR A,MCPHEE J,et al.A survey of stability enhancement strategies for articulated steer vehicles [J].International Journal of Heavy Vehicle Systems,200916(1/2):26- 48.
[5] 钟恒,陈树新.矿用铰接式电传动车辆转向控制的研究 [J].煤矿机械,2012,33(10):74-76.
ZHONG Heng,CHEN Shu-xin.Research on steer control for mining electric drive articulated vehicle [J].Coal Mine Machinery,2012,33(10):74-76.[6] 笪颖帆,倪文波,王雪梅,等.电驱动铰接式自卸车电子差速控制策略及仿真 [J].矿山机械,2015,43(4):29-33. DA Ying-fan,NI Wen-bo,WANG Xue-mei,et al.Electro-nic differential control strategy for electric-drive articulated dump truck and simulation [J]. Mining & Processing Equipment,2015,43(4):29-33.
[7] JIN Chun,WANG Ping,SHEN Yan-hua,et al.Differential control strategy based on an equal slip rate for an all-wheel electric-drive underground articulated dumping truck [J].Journal of Engineering Science and Technology Review,2014,7(4):163-168.
[8] 孙会来,申焱华,金纯,等.轮边电驱动铰接式矿用汽车差速控制策略研究 [J].农业机械学报,2014,45(11):27-33.
SUN Hui-lai,SHEN Yan-hua,JIN Chun,et al.Differential control strategy research of wheeled electric drive ADT mining truck [J].Transactions of the Chinese Society of Agricultural Machinery,2014,45(11):27-33.
[9] AZAD N L.Dynamic modelling and stability controller development for articulated steer vehicles [D].Waterloo:University of Waterloo,2006.
[10] 喻凡,林逸.汽车系统动力学 [M].北京:机械工业出版社,2012:211- 249.
[11] GIM G.An Analytical model of pneumatic tyres for vehicle dynamics simulations [J].International Journal of Vehicle Design,1990,11(6):589- 618;1991,12(1):19-39.
[12] 韩京清.自抗扰控制技术:估计补偿不确定因素的控制技术 [M].北京:国防工业出版社,2008:46-243.
[13] ZHAO S,GAO Z.An active disturbance rejection based approach to vibration suppression in two-inertia systems [J].Asian Journal of Control,2010,15(2):350-362.
[14] 姜立标,何家寿.两轮自平衡代步车控制策略及动力学仿真 [J].华南理工大学学报(自然科学版),2016,44(1):9-15.
JIANG Li-biao,HE Jia-shou.Control strategy and dyna-mic simulation of two-wheeled self-balancing vehicle [J].Journal of South China University of Technology(Natural Science Edition),2016,44(1):9-15.
[15] 靳立强,王庆年,宋传学.电动轮驱动汽车的最佳车轮滑移率实时识别 [J].吉林大学学报(工学版),2010,40(4):889-894.
JIN Li-qiang,WANG Qing-nian,SONG Chuan-xue.Real-time recognition strategy of optimal wheel slip rate for vehicle with motorized wheels [J].Journal of Jilin University(Engineering and Technology Edition),2010,40(4):889-894.
Differential Control Strategy and Simulation of Articulated Dump Truck with Six Electric Wheels
JIANGLi-biaoQIUHua-chuanLINGShi-yunHEJia-shou
(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)
The existing differential control strategies for the articulated dump truck with six electric wheels can simply achieve differential velocity. Moreover, they ignore yaw control and acceleration slip regulation, which causes the whole truck to show a poor dynamic performance. In order to solve these problems, a differential control strategy on the basis of the hierarchical control of driving force is proposed. Firstly, a dynamic mathematical model of the whole truck containing longitudinal, lateral, yaw and roll degrees of freedom is derived on the basis of Lagrange equation method. Then, the differential control strategy on the basis of the hierarchical control of driving force is designed, which is composed of the decision layer for total driving power and yaw control power, the distribution layer for differential drive and the stability layer for acceleration slip regulation. Finally, active disturbance rejection control algorithm is used to calculate the needed yaw control power to eliminate steering angle deviation, and optimal slip ratio recognition algorithm is used to amend the driving power of each wheel. The offline simulation results show that the proposed strategy can better realize the differential velocity of each wheel under different working conditions on the roads of different adhesion coefficients, and it can ensure better steering performance of the whole truck and better stability of each wheel.
articulated dump truck; electric wheel; differential control strategy; hierarchical control; active disturbance rejection control; offline simulation
1000-565X(2017)01- 0001- 08
2016- 05- 01
国家自然科学基金资助项目(51275175);广东省自然科学基金资助项目(2014A030313254)
Foundation items: Supported by the National Natural Science Foundation of China(51275175) and the Natural Science Foundation of Guangdong Province(2014A030313254)
姜立标(1965-),男,博士,副教授,主要从事车辆系统动力学与电子控制研究.E-mail:jlb620620@163.com
TP 273
10.3969/j.issn.1000-565X.2017.01.001

