基于变形协调设计的金属橡胶复合齿轮副振动研究*

王家序 黄伟 徐涛 肖科 李俊阳

(1. 重庆大学 机械传动国家重点实验室, 重庆 400044; 2. 四川大学 空天科学与工程学院, 四川 成都 610065)

基于变形协调设计的金属橡胶复合齿轮副振动研究*

王家序1,2黄伟1徐涛1肖科1李俊阳1

(1. 重庆大学 机械传动国家重点实验室, 重庆 400044; 2. 四川大学 空天科学与工程学院, 四川 成都 610065)

为解决传统齿轮副存在的回差问题,对设计、制造和安装过程中存在的误差影响因素进行了定量计算.通过考虑齿厚偏差、轴承径向跳动、中心距偏差和温度对齿轮变形的影响,提出了可自动变形补偿的金属橡胶复合齿轮副设计方法;基于ABAQUS有限元分析计算了高、低温对复合齿轮副变形的影响,得出了复合齿轮副在高、低温环境下的变形量和理论中心距预紧量;实验考察在不同预紧量下金属齿轮副和复合齿轮副的振动响应情况.结果表明:随着预紧量的增加,振动加速度先减小后增加;预紧量的改变对金属齿轮副的影响较大,对复合齿轮副的影响较小,复合齿轮副相对金属齿轮副的改善效果随着预紧量的增加而愈加明显;实验得到的最佳预紧量和仿真计算值基本吻合,从而验证了仿真分析的正确性.

金属橡胶复合齿轮副;变形协调;预紧量;振动

少齿差行星减速器具有体积小、传动比大、质量轻等优点,正广泛应用于航空航天、机器人等高精密传动领域[1- 4].渐开线圆柱齿轮副作为行星减速器的核心部分,其传动性能的好坏直接决定着整个减速器的性能.由于设计、加工和装配的误差,齿轮副之间通常存在齿侧间隙,而齿侧间隙会引起齿轮产生传动回差,从而导致传动系统动力输出和输入端的延时和滞后,不仅影响传动精度,还加剧了齿轮啮合时的冲击和振动.但过小的间隙又会造成齿轮干涉、增加摩擦磨损和影响润滑膜的形成[5],因此,要提高齿轮传动精度就必须合理地控制回差,如采用两套电机分别负责减速器正、反转的驱动方式或使用带弹簧预紧的双片组合齿轮来消除齿侧间隙;对设计、制造与装配工艺进行优化,如文献[6]针对K-H-V型行星减速器以总传动比和外形尺寸为约束,以回差最小化为目标开展了多目标优化设计.李俊阳等[7]针对渐开线内啮合圆柱齿轮副在制造及设计过程中出现的各项误差进行了归类分析及量化,提出了齿侧间隙控制与补偿方法;李新年[8]针对NN型少齿差行星减速器分析了其误差影响因素,提出了综合齿侧间隙的概念;徐畅等[9]针对滤波减速器应用概率统计的方法推导出齿轮副空程回差的数学计算公式,但不具有普适性;Kalantari等[10]研究了不同控制方法对齿面接触和间隙区域带来的不利影响;Nordin等[11]对近年来间隙装置的相关研究做了综述;Warnecke等[12]提出了在进入啮合侧隙区前通过输入额外的脉冲信号来补偿回差等.

文中以少齿差行星减速器中的关键传动部件行星齿轮副为研究对象,设计了一对全新的具有自适应变形补偿功能的金属橡胶复合齿轮副,提出了一种新的变形协调设计方法,利用金属橡胶固有的弹性性能，通过预紧补偿齿侧间隙及回差和自适应变形协调能力来消除间隙减小后的齿廓干涉、摩擦增大和噪音等问题,以提升少齿差行星齿轮的传动性能.

1 齿轮副齿侧间隙及回差计算

一对渐开线外啮合圆柱齿轮的侧隙主要是由两齿轮在齿厚方向的偏差和啮合中心距决定的,如图1所示,以分度圆上齿厚偏差量化的外啮合齿轮副的回差jφ可表示为

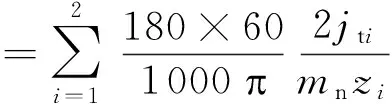
(1)

式中,jti为主/从动轮分度圆上侧隙,mn为被测齿轮副的法面模数,zi为主/从动轮的齿数.

图1 齿侧间隙示意图

在实际工程加工中,由齿厚偏差引起的侧隙通常不方便测量,一般都是采用量柱(球)测量跨距(表示为齿轮M值)来反映齿轮的齿厚偏差.齿厚偏差产生的齿轮侧隙(jti(EM))可用M值的偏差EM来表示,即

jti(EM)=EMitanα

(2)

由齿轮副的中心距误差Δe(以两齿轮基圆中心距计算)导致齿轮副产生的间隙为[5]

jti(Δe)=2Δetanα

(3)

齿轮副的中心距误差Δe主要是由齿轮径向跳动ΔFri、传动轴偏心误差Δfa与轴承径向游隙uri共同作用的结果.

外啮合齿轮副中心距误差如图2所示,O1、O2分别为主/从动轮的回转中心,A、B为基圆圆心,O1A、O2B为齿轮径向跳动、偏心误差和轴承径向游隙3个因素综合作用而导致齿轮回转中心与基圆中心的偏差,AB为实际啮合中心距.

图2 外啮合齿轮副中心距误差

如图2所示,假设主动轮以角速度ω1转动,经过t时间后转过θ1角度,从动轮转过θ2角度,且有θ1/θ2=z2/z1.此时实际中心距可表示为

AB=O1O2-O1Acosθ1-O2Bcosθ2

(4)

随着齿轮副的转动,中心距呈周期性变化,且齿轮啮合的理论最大值为

ABmax=O1O2+O1A+O2B

(5)

最小值为

ABmin=O1O2-O1A-O2B

(6)

考虑径向跳动公差ΔFri、传动轴偏心误差Δfa及轴承径向游隙uri等因数的共同作用,齿轮偏差为

(7)

式中,m、n分别为轴承的个数,并列轴承不重复计算.

文中的齿轮副参数为:mn=2.5,z1=27,z2=55,齿轮按7级精度设计,轴类零件形位公差按6级精度加工.测量小齿轮、复合齿轮齿圈的M值、径向跳动公差ΔFri以及输入输出齿轮安装轴的同轴度公差Δfai,轴承采用深沟球轴承61805,根据轴承手册[13]选取轴承游隙值.测得的复合齿轮副公差如表1所示.

表1 复合齿轮副公差参数

在实际工程应用中,由齿侧间隙引起的偏差通常以增大偏心距的方法予以补偿[14],但此方法容易在最小中心距处发生干涉.此外,在极端工况下还应考虑温度对齿轮变形的影响.低温时,外啮合齿轮的齿侧间隙会由于材料的收缩而增大,导致传动精度下降,振动与冲击加剧.高温时,外啮合齿轮的侧隙会随着材料的膨胀而减小,过大的热变形容易导致润滑失效、油膜不易形成、发生 “卡死”或“卡涩”等现象,最终造成齿面磨损、传动精度下降、振动和噪声增大等问题.因此,温度对齿轮传动副变形的影响应该被充分考虑.

为解决上述问题,文中设计了一对可供自适应变形协调的金属橡胶复合齿轮,其结构如图3所示.

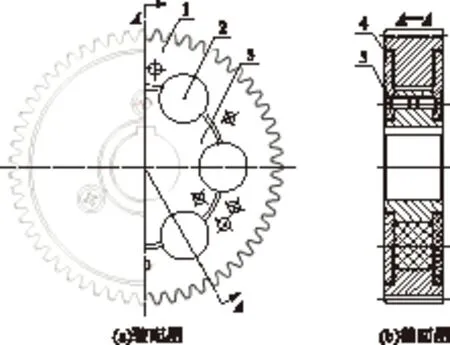
1—齿圈;2—金属橡胶材料;3—轮毂;4—挡圈;5—螺钉

如图3所示,金属橡胶复合齿轮是将一个完整的齿轮切割开,并在其间隙填充金属橡胶弹性材料.复合齿轮副主要由齿圈、金属橡胶和轮毂3大部分构成,且齿圈和轮毂之间设计有一定的间隙可供变形协调.复合齿轮副的作用机理为：金属橡胶弹性体在一定程度上能够对冷热变形起到一定的自适应变形协调作用,低温时通过预紧减小中心距来补偿因低温收缩而导致的间隙增加;高温时虽然热变形导致齿轮副的间隙减小,但金属橡胶弹性体在径向力作用下会发生一定的压缩变形,从而保证齿轮副不会因变形过大而出现“卡死”和“卡涩”现象.为了计算简便,假设由温度导致的齿轮副变形量为ΔaT,中心距预紧量为Δaj,此时中心距可表示为

(8)

金属橡胶复合齿轮副的变形协调设计流程如图4所示.

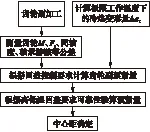
图4 变形协调设计流程图

2 复合齿轮副冷热变形分析计算

在实际工作中,齿轮副的传动中心距会随着传动过程中齿面摩擦和外界环境温度的改变而改变.在低温情况下,一般可以人为预紧保证传动精度;在高温情况下,复合齿轮副中的弹性体可通过径向变形来保证齿轮副即使在零侧隙下也不发生“卡死”.而传统的金属齿轮副无法补偿热变形.进一步考虑到齿轮副在运行过程中的摩擦和润滑生热等复杂情况,文中通过ABAQUS有限元仿真软件对极端工况下的复合齿轮副开展冷热变形分析,初步计算得到在两种极端工况下所需的预紧量.

2.1 齿轮副材料设置

在开展齿轮副的热变形分析过程中,材料的力学参数起着至关重要的作用,其最基本的参数包括材料密度、弹性模量、泊松比和线性膨胀率等.在齿轮副的设计中,小齿轮、复合齿轮的齿圈和轮毂均采用40Cr调质钢[15],密度为7.85 g/cm3,弹性模量为1.82×105MPa,泊松比为0.31.金属橡胶的材料为304不锈钢,密度为2.75 g/cm3,弹性模量为18.94 MPa,泊松比为0.34.相对密度为0.35,丝径大小为0.3 mm.2.2 齿轮副建模分析

在Solidworks软件中建立齿轮副三维模型,将建好的三维模型通过中性文件导入ABAQUS软件中.在不影响分析结果和获得较高网格质量的情况下,忽略齿轮倒角和键槽,去掉无关的挡圈和螺钉,只保留小齿轮、复合齿轮齿圈、轮毂和弹性体.选择通用静力分析步,建立一个名为Step-heat的分析步.边界条件设置需将复合齿轮和小齿轮的轴孔进行完全约束.初始载荷温度设置为25 ℃并将温度场传递至下一个分析步Step-heat,分别设置该分析步的温度为-50 ℃和80 ℃.热传导率以金属对金属的热传导率为参考,常温下为16.7 W/(m·K).选用网格质量较好的六面体单元以扫略方式进行划分,完成的网格模型如图5所示,共计381 746个单元、431 980个节点.

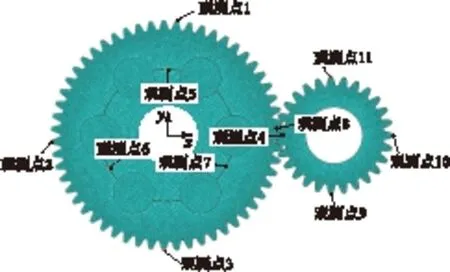
图5 复合齿轮副的网格划分和观测点位置

Fig.5 Mesh division and position of observation points of compound gear pair

为获得较准确的计算结果,在复合齿轮齿圈和小齿轮的齿顶圆上分别取4个观测点用于测量热变形后的径向变形量,用其平均值作为最终热变形量.观测点位置如图5所示.

2.3 冷热变形分析结果

图6所示为复合齿轮副在-50 ℃、80 ℃下x方向的位移云图.由于文中开展的变形协调设计不需要轴向的(图中z向)冷热变形量,因此忽略观测点在z方向的变形量,取x向位移U1和y向位移U2合成总的径向位移.小齿轮与复合齿轮齿圈上各参考点在-50 ℃、80 ℃下变形前后的坐标值如表2所示.

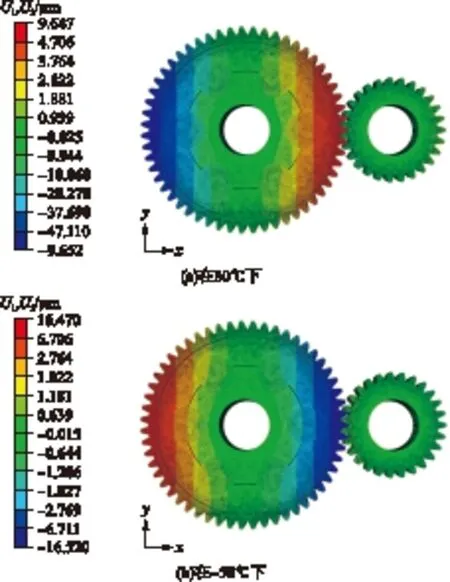
图6 复合齿轮副在x方向的冷热变形位移云图

Fig.6 Hot and cold deformation displacement of compound gear pair atxdirection

由表2可知,在80 ℃高温下,取复合齿轮齿圈上观测点1、2、3和4的径向位移的平均值作为复合齿轮齿圈在该温度下的径向变形量(ΔaHT2=9.45 μm),取小齿轮上观测点8、9、10和11的径向变形量的平均值作为小齿轮在该温度下的径向变形量(ΔaHT1=3.09 μm);在-50 ℃低温工况下,取复合齿轮齿圈4个观测点的径向位移量的平均值作为齿圈在低温时的径向变形量(ΔaLT2=-10.43 μm),取小齿轮上4个观测点的径向位移量的平均值作为小齿轮在低温下的径向变形量(ΔaLT1=-4.01 μm).

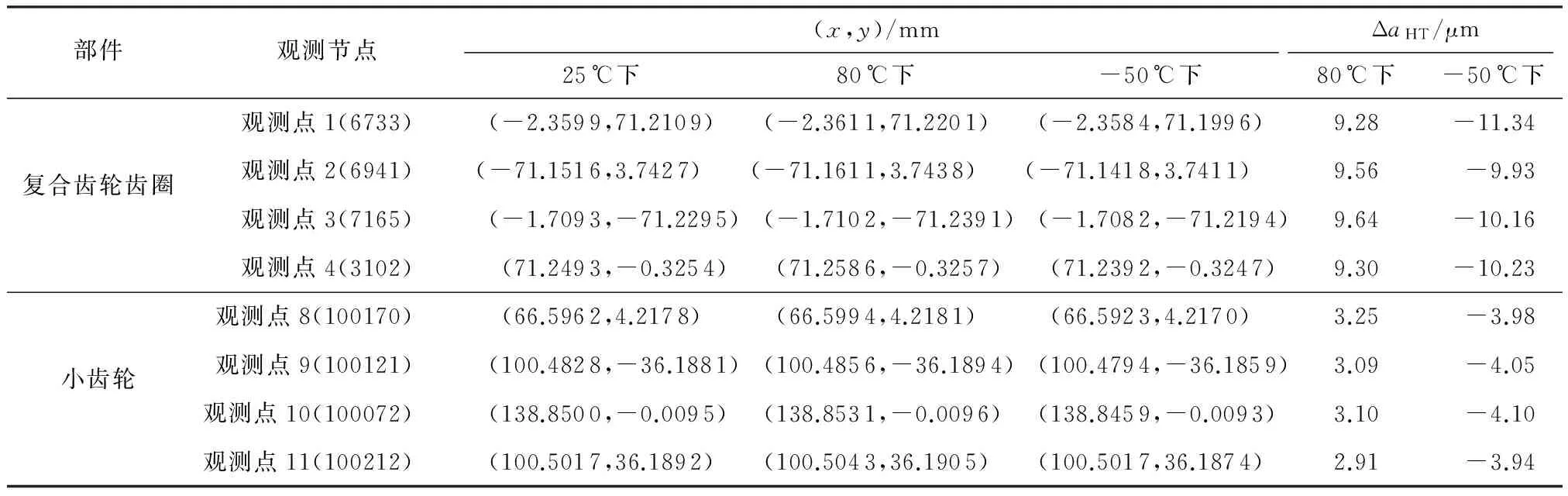
表2 复合齿轮副在不同温度下的变形结果

另外,在80 ℃环境下,为避免由于高温膨胀导致齿圈和轮毂发生干涉,需考虑复合齿轮副齿圈和轮毂间的间隙变化量.在齿圈和轮毂的分界面上分别取3个观测点(观测点5、6、7),以考察温度对齿圈和轮毂间隙的影响,观测点位置如图6所示.每个观测点是指在相邻分界面上齿圈和轮毂的两个较接近的点.获得的齿圈和轮毂的热变形结果见表3.由表中可知,取复合齿轮齿圈和轮毂之间间隙在观测点5、6和7处的径向位移量的平均值作为齿圈和轮毂间隙在高温时的位移变化量ΔrHT=-6.06 μm.

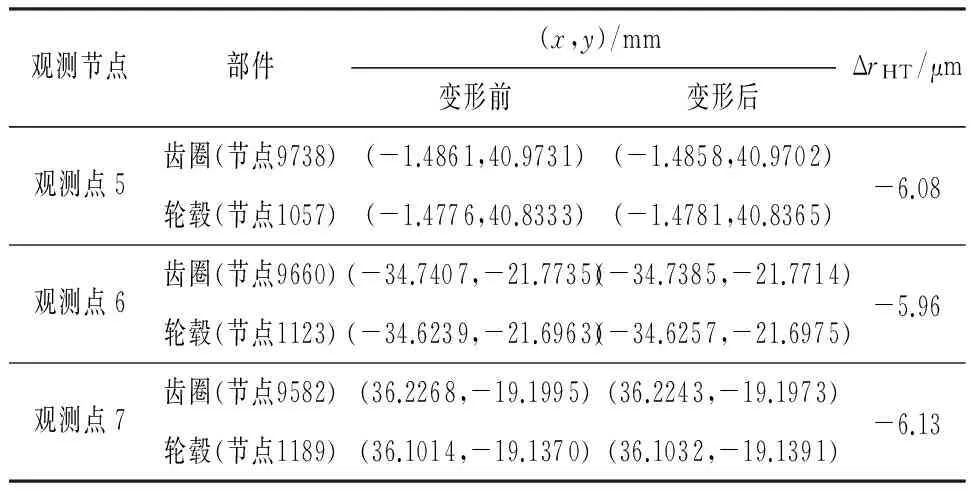
表3 齿圈和轮毂在80 ℃时的变形结果

3 复合齿轮副预紧量计算及可靠性验算

3.1 常温下预紧量计算

在常温(25 ℃)下,要计算复合齿轮副的预紧量,复合齿轮副回差需控制在3′以内[9].在常温情况下，由于不考虑温度的影响,此时取中心距最大,在此条件下小齿轮和复合齿轮的中心距误差Δe1、Δe2分别为

(9)

结合式(2)、(3)得到小齿轮和复合齿轮的齿侧间隙jt1和jt2：

(10)

式中,Δaj前的负号表示减小中心距,有利于控制回差.再结合式(1)可以求出复合齿轮副在常温下的预紧量Δaj=7μm,即装配中心距a′=102.493mm.

3.2 高温时回差可靠性验算

在高温条件下,齿侧间隙会随着材料的膨胀而减小,导致齿面间摩擦加剧、传动性能降低.虽然复合齿轮副具有特殊的变形补偿功能,但这一补偿功能的前提是金属橡胶的变形量小于等于齿圈和轮毂的单边间隙.考虑到测量和计算过程中存在的误差,文中对极限高温情况需保留一定的余量,初步设定80 ℃高温下的安全间隙为齿圈和轮毂初始间隙的10%[10],并以该限定条件作为可靠性验证条件.则在考虑预紧量的情况下齿轮副的中心距误差为

Δe=-Δe1-Δe2-Δaj

(11)

在高温条件下,复合齿轮副之间会产生挤压变形,导致复合齿轮齿圈和轮毂之间的间隙减小.由于金属橡胶的弹性模量远小于金属材料,故可认为由热变形引起的齿轮副挤压变形全部由金属橡胶弹性体承担,此时可将复合齿轮副中心距的误差用齿圈和轮毂间的间隙改变量来表示,即

ΔeHT=Δe-ΔaHT1-ΔaHT2

(12)

考虑到齿轮副自身的变形量ΔrHT,则齿圈和轮毂的实际间隙可表示为

Δr′=Δr+ΔrHT+ΔeHT

(13)

文中涉及的复合齿轮设计间隙Δr=0.14mm,结合式(9)、(11)-(13)及前面计算得到的热变形量可求出齿圈和轮毂在高温条件下的实际间隙Δr′=45.4μm,安全余量为32.43%(大于10%),故满足设计要求.

3.3 低温时回差可靠性验算

在低温情况下,齿侧间隙因材料的收缩而增大,此时可按照回差控制在6′内进行可靠性验算[9].在低温条件下,小齿轮和复合齿轮的中心距误差为

(14)

忽略温度对M值的影响,结合式(1)、(9)、(10)及表1中的误差值可求得低温条件下金属橡胶复合齿轮副的回差jφ=5.238′<6′,满足回差设计要求.

4 传动特性实验

为进一步分析复合齿轮副在不同侧隙下的振动特性,实验中加入了一组与复合齿轮副完全一样的全金属齿轮副作为对比实验,其中全金属齿轮副的齿数和转动惯量与复合齿轮副完全相同.实验中通过改变齿轮副的预紧量分别获得两组齿轮副在不同预紧量下的振动情况,结果表明，金属橡胶弹性体的加入能有效改善齿轮副的振动特性.实验样件如图7所示.

图7 金属橡胶复合齿轮副和金属齿轮副样件

按照国家标准《验收试验中齿轮装置机械振动的测定》(GB8543—1987)规定,文中在SKLMT多用途传动摩擦学实验台CQU-AMH-195上完成实验,该实验装置也可开展齿轮副、带传动、链传动等传动副的综合性能实验.由于该实验台没有配套的角度编码器,因此无法开展传动精度及回差测试,文中仅开展了齿轮副的振动响应实验.多用途传动摩擦实验台如图8所示.

在实验过程中,按照常用工况设置主轴1转速为1 000r/min,主轴2负载为50Nm.在保证金属齿轮不出现“卡死”的情况下,以0.005mm为单位预紧量调整复合齿轮副和金属齿轮副的传动中心距,两齿轮副的标准中心距均为102.5 mm.为了验证齿轮副预紧量与齿轮振动特性的关系和得到最佳振动特性的预紧量,取齿轮副的预紧量为-0.015、-0.010、-0.005、0.000、0.005和0.010 mm,得到金属齿轮副与复合齿轮副的加速度振动响应如图9、图10所示(a、a′分别为时域和频域的加速度幅值),金属齿轮副和复合齿轮副输出轴的振动加速度峰峰值与均方根值(RMS)对比如表4所示,并以均方根值为优化目标,得到复合齿轮副相对于金属齿轮副的振动加速度改善率.

图8 多用途传动摩擦试验台

图9 金属齿轮副在不同预紧量下输出轴y方向的振动加速度

图10 复合齿轮副在不同预紧量下输出轴y方向的振动加速度

表4 金属齿轮副和复合齿轮副输出轴的振动加速度峰峰值与RMS

Table 4 Acceleration peaks and RMS on output shaft of metal gear pair and compound gear pair

预紧量/mm峰峰值/(m·s-2)RMS/(m·s-2)振动加速度改善率/%金属齿轮副复合齿轮副金属齿轮副复合齿轮副-0.0154.94082.81870.45860.180560.64-0.0104.68532.20110.38490.163857.44-0.0053.62771.43480.23370.110252.850.0003.91391.64490.25380.131148.350.0054.20272.06350.28730.184335.850.0104.60562.41490.32910.207436.98

从图9、图10可知,以预紧量0为起点,随着中心距的减小,复合齿轮副与金属齿轮副输出轴的振动加速度均呈先减小后增大的趋势.先减小主要是因为在标准中心距下,齿轮副之间存在一定的齿侧间隙,从而导致了啮合冲击;在预紧量减小时,齿侧间隙减小,齿轮啮合冲击减小,振动响应有所改善;随着预紧量的进一步增大,过大的预紧量导致齿面发生挤压,摩擦力相应增大,振动加剧.以标准中心距为起点,随着中心距的增加,两齿轮副输出轴的振动加速度也随之增加,这主要是因为中心距的增加使齿轮副之间的齿侧间隙变大,从而导致回差增大,振动冲击增加.

从表4可知,复合齿轮副的峰峰值和RMS值均明显小于金属齿轮副,说明其振动特性优于金属齿轮副,这主要是因为金属橡胶弹性材料的加入能很好地抑制齿轮传动过程中的振动,使传动过程更加平稳.随着预紧量的增大,复合齿轮副的优越性表现得愈加明显,其振动加速度的RMS值改善率越大.这表明金属橡胶复合齿轮副具有强大的变形补偿功能,且复合齿轮副振动最佳预紧量范围为-0.005～-0.010 mm.

5 结论

文中定量分析了齿轮副的设计、加工以及装配误差对齿侧间隙的影响,基于可供变形协调设计得到金属橡胶复合齿轮副的实际中心距;提出了金属橡胶复合齿轮副的变形协调方法,基于ABAQUS有限元分析软件对复合齿轮副进行冷热变形仿真分析,得到了高、低温环境下复合齿轮副的变形量,计算出其对应的预紧量,并进行可靠性验证.实验结果表明:随着预紧量的增加,齿轮副的振动加速度先减小后增加;预紧量的改变对金属齿轮副的影响较大,对复合齿轮副的影响相对较小,金属橡胶复合齿轮副具有很好的自适应变形协调能力.

实验得到最佳振动的预紧量和仿真计算值比较吻合,表明了仿真的可行性.该实验为后续金属橡胶复合齿轮副的进一步研究奠定了基础,为少齿差行星减速器结构的进一步优化和减震降噪提供了重要的参考.

[1] PATRICK R,ORCHARD M E,ZHANG Bin,et al.An integrated approach to helicopter planetary gear fault diagnosis and failure prognosis [C]∥Proceedings of the 42nd Annual Systems Readiness Technology Conference.Baltimore:IEEE,2007:547-552.

[2] 赵韩,吴其林,黄康,等.国内齿轮研究现状及问题研究 [J].机械工程学报,2013,49(19):11-15.

ZHAO Han,WU Qi-lin,HUANG Kang,et al.Status and problem research on gear study [J].Journal of Mechanical Engineering,2013,49(19):11-15.

[3] 梁锡昌,吕红展.减速器的分类创新研究 [J].机械工程学报,2011,47(7):1-7.

LIANG Xi-chang,LÜ Hong-zhan.Research on categorizing innovation of speed reducers [J].Journal of Mechanical Engineering,2011,47(7):1-7.

[4] 余波.飞行器舵机传动机构设计与分析 [D].重庆:重庆大学,2014.

[5] 王家序,秦德成,张林川,等.滤波减速器轮齿表面瞬态微观弹流润滑模型 [J].四川大学学报(工程科学版),2013,45(1):202- 207.

WANG Jia-xu,QIN De-cheng,ZHANG Lin-chuan,et al.Transient thermal micro-elastohydrodynamic lubrication model of filtering reducer [J].Journal of Sichuan University(Engineering Science Edition),2013,45(1):202- 207.

[6] 王国华,陈明,胡建国.行星齿轮减速器基于回差分析的优化设计 [J].机械设计与研究,2005,21(3):56-58.

WANG Guo-hua,CHEN Ming,HU Jian-guo.Optimal design of planetary gear reducers based on backlash analysis [J].Machine Design and Research,2005,21(3): 56-58.

[7] 李俊阳,王家序,肖科,等.渐开线内啮合圆柱齿轮副的回差控制与补偿 [J].重庆大学学报,2012,35(7):43- 48.

LI Jun-yang,WANG Jia-xu,XIAO Ke,et al.Backlash control and compensation for internal meshing involute spur gears [J].Journal of Chongqing University,2012,35(7): 43- 48.

[8] 李新年.高精度少齿差减速器的传动回差精度控制 [J].船舶工程,2003,25(6):28-30.

LI Xin-nian.Accuracy control of driving backlash of speed-reducer with high accuracy and low gear-tooth error [J].Journal of Ship Engineering,2003,25(6):28-30.

[9] 徐畅,王家序,肖科,等.基于概率理论的滤波减速器空程回差计算及分析 [J].机械传动,2010,34(12):1-5.

XU Chang,WANG Jia-xu,XIAO Ke,et al.Calculation and analysis on return difference of filtering gear reducer based on probability theory [J].Journal of Mechanical Transmission,2010,34(12):1-5.

[10] KALANTARI R,FOOMANI M S.Backlash nonlinearity modeling and adaptive controller design for an electromechanical power transmission system [J].Scientia Iranica Transaction B:Mechanical Engineering,2009,16 (6):463- 469.

[11] NORDIN M,GUTMAN P O.Controlling mechanical systems with backlash a survey [J].Automatica,2002,38(10):1633-1649.

[12] WARNECKE M,JOUANEH M.Backlash compensation in gear trains by means of open-loop modification of the input trajectory [J].Journal of Mechanical Design,2003,125(3):620- 624.

[13] 秦大同,谢里阳.现代机械设计手册 [M].北京:北京化工工业出版社,2013:39- 40.

[14] 李俊阳,王家序,周广武,等.渐开线少齿差行星传动的变形协调设计 [J].中国机械工程,2014,25(5):576-580.

LI Jun-yang,WANG Jia-xu,ZHOU Guang-wu,et al.Deformation and compatibility design of involute planetary gear drive with small teeth difference [J].China Mechanical Engineering,2014,25(5):576-580.

[15] 刘轶群,董冬,胥德峰.温度对40Cr钢弹性模量影响的实验研究 [J].实验技术与实验机,2005,45(1):23- 24.

LIU Yi-qun,DONG Dong,XU De-feng.Experimental study on the effect of temperature on elastic of 40Cr steel [J].Journal of Experimental Technique and Expe-rimental Machine,2005,45(1):23- 24.

Investigation into Vibration of Metal Rubber Compound Gear Pair Based on Deformation Coordination Design

WANGJia-xu1,2HUANGWei1XUTao1XIAOKe1LIJun-yang1

(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;2. School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, Sichuan, China)

In order to solve the return difference problem of traditional gear pairs, the factors influencing the errors in the processes of design, manufacture and installation are quantitatively calculated. Then, by taking into account the influences of tooth thickness deviation, radial pulsation, center distance deviation and temperature on gear deformation, a design method of the metal rubber compound gear pair with automatic deformation compensation is proposed. Moreover, on the basis of ABAQUS finite element analysis, the influences of high and low temperatures on the gear deformation are calculated, and the gear deformations at the high and low temperatures as well as the preloading of theoretical center distance are obtained. Finally, the vibration responses of the metal and compound gear pairs under different preloading are tested. The results show that (1) with the increase of the preloading, the vibration acceleration decreases first and then increases; (2) the preloading has a great influence on the metal gear pair but a little influence on the compound gear pair, and with the increase of the preloading, the improvement effect of the compound gear pair tends to become more obvious than that of the metal gear pair; and (3) the optimal preloading obtained by tests accords well with the calculated result, which verifies the correctness of simulation analysis.

metal rubber compound gear pair; deformation coordination; preloading; vibration

1000-565X(2017)01- 0129- 08

2016- 03- 28

国家自然科学基金资助项目(51375506,51475051,51505045);国家“863”计划项目(2015AA043001);重庆大学中央高校基本科研业务费专项资金资助项目(CDJZR14280001);重庆市研究生科研创新项目(CYB16027)

Foundation items： Supported by the National Natural Science Foundation of China(51375506,51475051,51505045) and the National High-Tech R&D Program (863 Program) of China(2015AA043001)

王家序(1954-),男,教授,博士生导师,主要从事机电传动与智能控制技术、机械摩檫学与特种摩擦副技术研究.E-mail:jxwang@cqu.edu.cn

TH 132.417

10.3969/j.issn.1000-565X.2017.01.019