公路隧道群交通事故非线性综合预测方法研究

杨 健，阳富强，沈斐敏

(1.福州大学土木工程学院，福建 福州 350116；2.福州大学环境与资源学院，福建 福州 350116)

公路隧道群交通事故非线性综合预测方法研究

杨 健1,2，阳富强2，沈斐敏2

(1.福州大学土木工程学院，福建 福州 350116；2.福州大学环境与资源学院，福建 福州 350116)

以沈海高速罗长段隧道群交通事故为预测对象，以相对交通事故频数为预测目标，针对隧道群交通系统非线性、动态的特点，研究基于BP神经网络的交通事故非线性综合预测方法.结果表明，非线性综合预测方法能综合指数平滑模型、非线性回归模型、灰色马尔科夫模型等单一预测模型的有效隐含信息，提高交通事故的预测精度，为优化交通事故预测技术指出新方向.通过该方法预测，随着交通量的增加，未来3年(2016-2018年)罗长高速隧道群交通事故频数将呈现先下降后急剧上升的变化过程.

隧道群；相对交通事故频数；非线性预测；综合预测方法

0 引言

近年来，我国公路隧道建设得到飞速发展，施工技术日益成熟，公路隧道总长持续高速增长，平均年增速度超过24%，到2015年底，公路隧道共计14 006处，长达1 268.39万延米[1].但与隧道建设高速发展鲜明对比的是，我国公路隧道运营管理技术较国外先进水平还存在不少差距[2].与此同时，由于公路隧道结构设施复杂、地理位置偏僻、逃生疏散困难，一旦发生事故往往造成惨重的人员伤亡和重大的财产损失，因此隧道运营安全问题日益显现[3].事故预测是隧道运营安全管理的一项基础工作，旨在对已发生事故历史资料的统计和分析，采取有效的预测技术和手段，分析事故发生的规律特性，从而对事故的未来状态进行估计和推测[4].根据预测结果制定相应的预控措施，降低事故发生的可能性，起到防患于未然的效果.可以说，事故预测技术的发展对提高隧道运营管理技术具有重要的促进作用.

当前，国际上公认的经典交通事故预测模型有Smeed模型[5]、Alligaier模型[6]、Navin模型[7]、Oppe模型[8]等等.但这些模型均仅从交通安全系统的某一个侧面反映问题，不能很好适用于国内隧道群交通系统.此外，国内外学者还提出许多确定型或非确定型的单一预测模型，例如灰色模型、回归模型、时间序列模型、马尔科夫模型、指数平滑模型等等.但这些单一模型各有特点，且在不同时刻表现出不同的精度，单纯依据某一判定标准选取或舍弃某种模型，势必会造成部分有用信息的丢失[9].另外，公路隧道群交通系统是一个非线性、动态、复杂的“巨系统”，受众多错综复杂因素的影响，如果试图使用某一种预测模型来拟合或预测交通事故的变化规律是十分困难的[10].Bates和Granger最早提出综合预测(也称复合预测或组合预测)的思想[11]，它将不同的单一事故预测模型以适当的形式进行融合，综合单个模型的有用隐含信息，使其适用于交通事故时间序列预测，改善预测效果[12].但如何构建综合预测模型，需要进一步深入研究.

本研究以沈海高速罗长段隧道群为背景，采用综合预测方法对公路隧道群交通事故发展趋势进行预测.首先分析指数平滑、非线性回归、灰色模型等单一预测模型对公路隧道群交通系统内部规律的描述，并对其进行优化改进，而后建立基于BP神经网络的非线性综合预测模型.最后通过对各种模型预测结果精度进行对比分析，验证综合预测方法的可行性和有效性.

1 预测对象及指标

选取沈海高速罗长段(罗长高速)隧道群的交通事故为预测对象.罗长高速具有交通量大、桥隧占比高、地形复杂、交通事故频发的特点，全线共有隧道14座，于2002年12月20日正式通车.通过调研，鉴于通车伊始交通量偏少，故舍弃起始3年的数据，以2005-2015年的交通事故数据作为预测对象的样本容量.

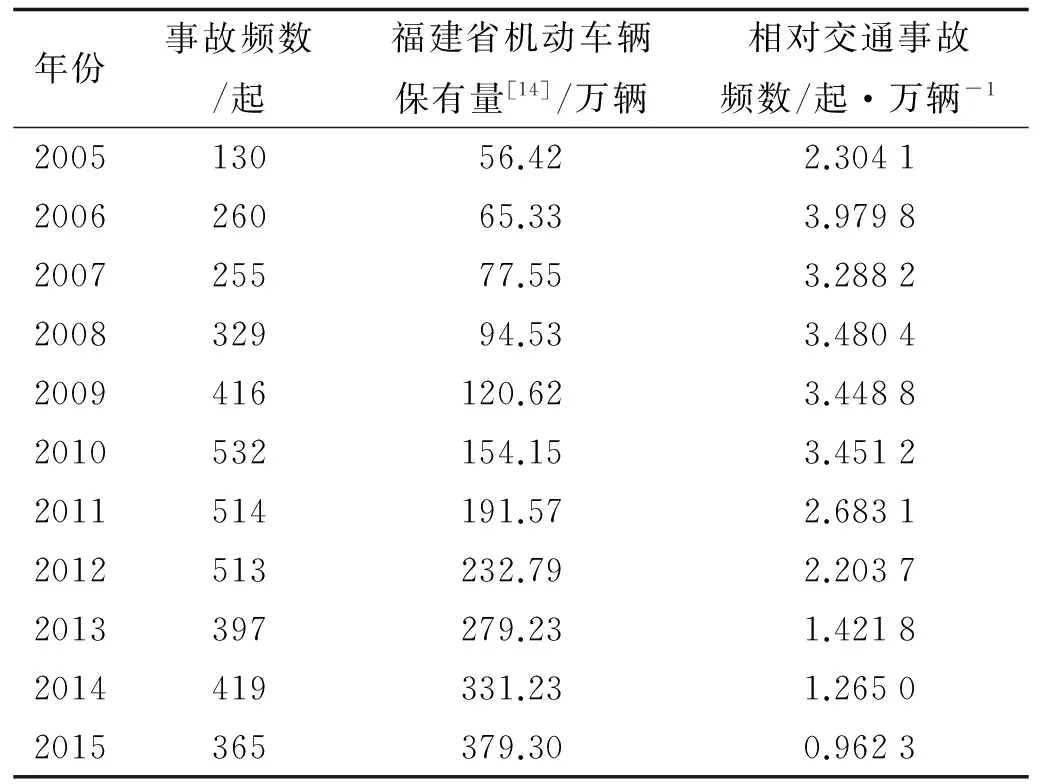
表1 2005-2015年罗长高速公路隧道群交通事故 统计数据Tab.1 Statistical data of traffic accident in highway tunnel group (2005 to 2015)

公路隧道群交通系统是受众多因素交错影响的复杂系统，但要把所有因素都考虑进来是难以实现的，同时也会大大减少样本量[13].从统计学的角度，公路隧道交通量越大，发生交通事故频数或几率也越大，故应考虑交通量对交通事故频数的影响.鉴于实时交通量数据获取难度大，选取福建省机动车辆保有量来近似表征交通量，从而得到相对交通事故频数.选取公路隧道群相对交通事故频数为预测指标，样本数据详见表1.

2 单一预测模型

2.1 指数平滑模型

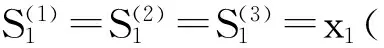
根据式(1)，所得计算结果详见表2，其拟合平均误差为20.98%，预测误差为36.61%，精度较低.

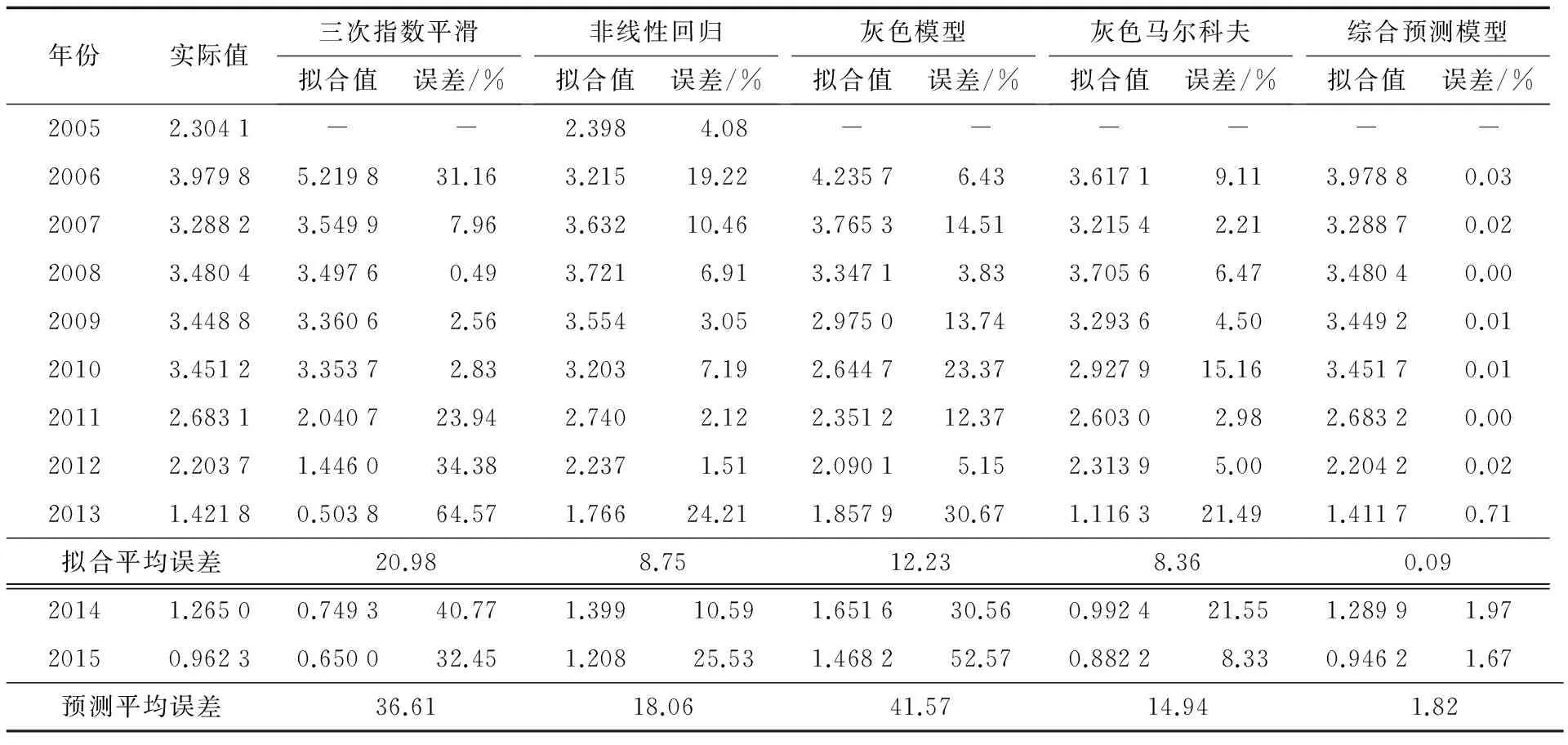
表2 各预测模型预测结果对比分析数据表Tab.2 Data of comparison and analysis of the forecast results of each forecast model

注:各模型实际值和拟合值的单位均为起·万辆-1

2.2 非线性回归模型

根据非线性回归模型理论，以样本数据中2005-2013年的相对交通事故频数x为因变量，相应的年份t为自变量，则对某个观测变量(ti,xi),i=1，2，…，n，可表示为：

根据式(3)，所得计算结果详见表2，其拟合平均误差为8.75%，预测误差为18.06%，精度一般.

2.3 改进灰色模型GM(1，1)

灰色预测方法是一种对数据序列动态的分析方法，计算简便、快捷，但对数据序列的要求较高，且长期预测的精度较差[15].而马尔科夫模型对于波动性较大的数据序列预测精度较高，基于灰色预测方法构建灰色马尔科夫模型[16].故本文首先进行灰色模型GM(1，1)预测，而后用马尔科夫链对预测结果进行优化，以提高预测精度.

利用Matlab编程建立灰色模型GM(1，1)，以2005-2013年的相对事故频数作为样本数据，所得计算结果详见表2，其拟合平均误差为12.23%，预测误差41.57%，精度较差.因此，以灰色模型的预测值作为马尔科夫模型的样本数据对预测结果进行优化.根据拟合误差将数据序列划分为3个状态，并建立转移概率矩阵，用每个预测灰区间的中位数作为下一时刻预测值的相对值.所得灰色马尔科夫预测的计算结果详见表2，其拟合平均相对误差为8.36%，预测误差为14.94%，精度一般，但明显优于灰色模型.

3 非线性综合预测模型

3.1 综合预测理论设计

假定为公路隧道群交通事故预测提供n种单一预测模型，第i(i∈n)种单一预测模型可表示为从m维欧式空间的一个子集X到n维欧式空间子集Y的映射[17]，即：

式中：ψti表示t时刻第i种单一公路预测模型的隧道交通事故预测值.

根据单一预测模式的映射原理，对于t时刻公路隧道群交通事故预测值，用组合函数表示为：

式中：yt表示t时刻综合预测模式下公路隧道群交通事故预测值.式(5)为公路隧道群交通事故综合预测模式函数关系式，而如何构建函数F(x)，是综合预测模型的核心研究问题.

3.2 基于BP神经网络的综合预测模型

事实上，在构建综合预测模型时，难以确定一个稳定的、统一的非线性显式函数F(x)来满足交通系统的所有动态变化需求，故函数F(x)自身也应具有动态性、非线性和自适应性的特点.BP神经网络是基于误差反向传播算法的人工神经网络，具有高度非线性映射能力、容错能力和自适应能力，即给定∀ε>0和任意L2函数f:[0，1]n→Rm，均存在一个BP神经网络，使得在任意ε平方误差内逼近f.因此，利用BP神经网络的非线性逼近能力，确定非线性函数F(x).模型的构建分以下几步实现：

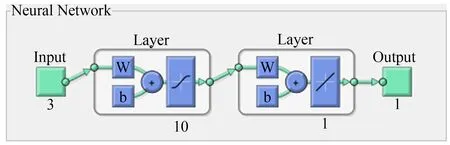
图1 三层神经网络结构图Fig.1 Structure of three layers neural network

Step1 确定网络结构.研究证明，各层均采用S型函数的3层BP神经网络可对任意复杂的非线性函数的逼近问题进行处理[18].将上述三种单一预测模型得到的预测值作为输入因子，各年公路隧道群相对交通事故频数的实际值作为输出因子，即输入神经单元数为3，输出神经单元数为1，则构成了3-j-1结构的神经网络模型.而隐含层神经元的数目j的确定目前没有一个统一的结论，增加隐含层的神经个数可以提高预测模型的精度，但同时会降低网络训练的效率[18].结合此观点并通过试算，确定当隐含层的神经元数目为10时，模型精度和收敛速度均能满足较好的要求.即构成三层神经网络结构如图1所示.

Step2 建立学习样本矩阵.由前述3种单一预测方法得出2006-2013年的拟合值构成的输入学习样本矩阵，如下所示：

Step3 选取训练学习算法参数.选取Tansig-purelin为激活函数，采用加动量项因子改进最速下降法的Traingdx训练函数进行神经网络连接权系数和网络阈值训练和学习.训练时，训练学习次数k=10 000次，学习速率η=0.01、训练精度E=0.000 1.

Step4 综合预测结果输出.利用MATLAB编制程序，进行训练学习，收敛后得到输出层的预测值，所得结果填入表2，其拟合平均误差为0.09%，预测误差为1.82%，预测精度高.

4 结果对比分析

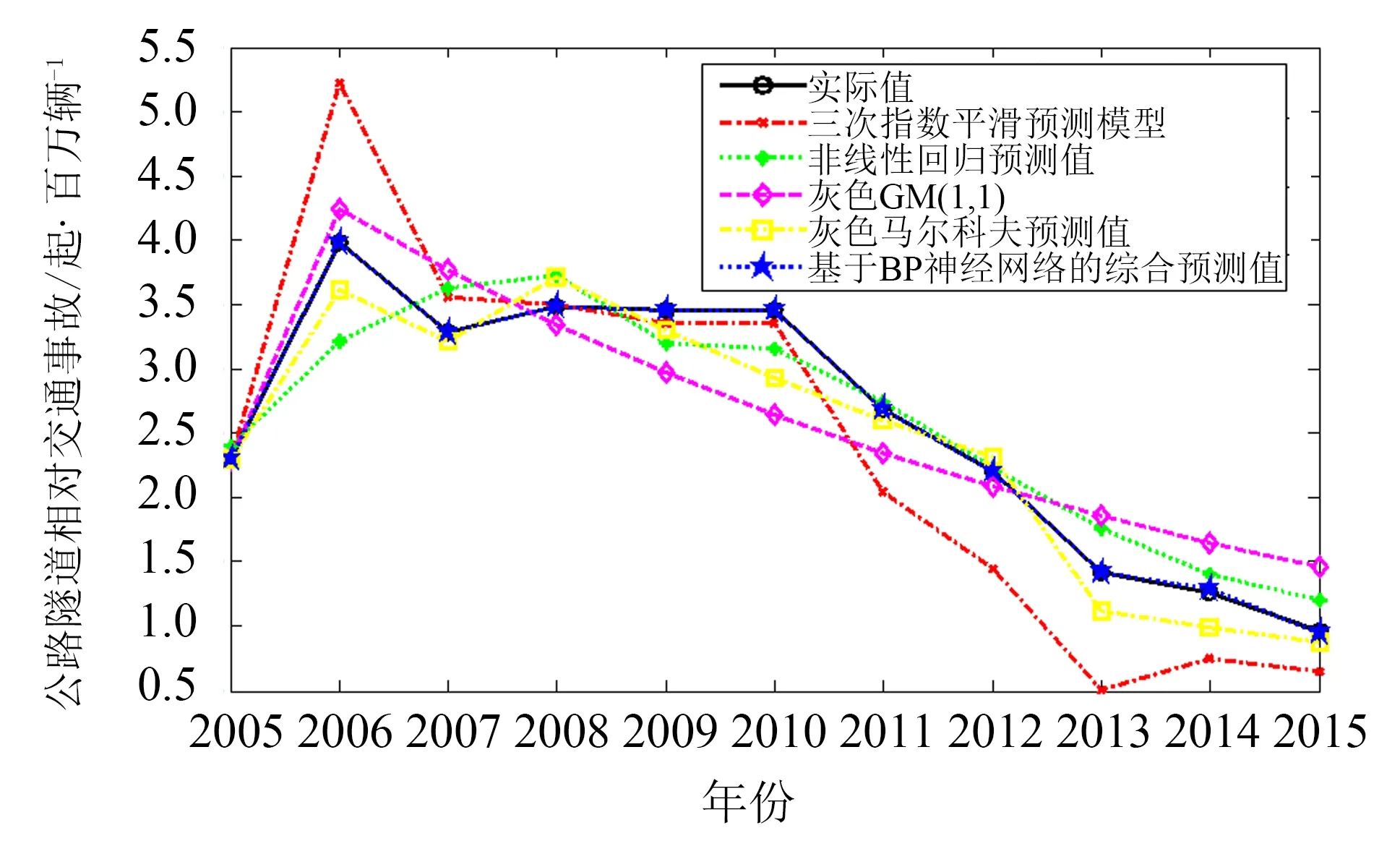
图2 各类预测模型的预测结果对比Fig.2 Comparison of prediction results of each forecasting model

上述各单一预测模型、综合预测方法的预测结果和实际值的对比，如图2所示.

由图2可得以下3个主要结果：

1)各单一预测方法中，三次指数平滑、非线性回归和灰色模型的拟合和预测精度无一致性，且预测结果均不大理想.特别是灰色模型的预测误差超过了40%，但通过与马尔科夫模型结合，预测精度得到明显提升，预测平均误差小于15%.表明综合模型用于公路隧道群事故预测的思路是可行的，它能够综合各单一模型的有效隐含预测信息，提高预测精度.

2)基于BP神经网络的非线性综合预测模型相较于单一预测模型的预测精度有更进一步提高，表明具有高度非线性映射能力的BP神经网络能够用于建立综合预测模型，很好地满足了公路隧道群交通系统的非线性、动态变化的需求.

表3 相对交通事故频数预测值
Tab.3 Forecast value of relative traffic accident frequency

年份201620172018预测值0.96580.63521.3459

3)根据非线性综合预测模型，再以2005-2015年的公路隧道群相对交通事故频数为预测训练样本，预测了未来3年(2016-2018年)相对交通事故，预测结果如表3所示.可以看出，受交通量、道路状况、管理水平、工程技术等各种因素的影响，交通事故频数依然居高不下.

5 结语

1)以罗长高速公路隧道群2002-2015年相对交通事故频数为样本数据，构建指数平滑预测模型、非线性回归预测模型和灰色马尔科夫预测模型等预测模型，对比分析各模型的拟合和预测精度，表明各模型具有各自特点，均能为预测提供相应的有效隐含信息.

2)研究基于BP神经网络的非线性综合预测方法，通过与单一预测模型的对比分析，发现综合预测模型预测精度明显优于其他单一预测模型，表明基于BP神经网络的非线性综合预测方法能够满足公路隧道群交通系统的非线性动态需求，达到优化预测结果的目的.

3)根据综合预测结果，未来3年(2016-2018年)相对交通事故分别是0.965 8、0.635 2和1.345 9，也即在2017年相对事故频数得到较好控制，但在2018年将会有较大增加.若以过去3年福建省人均汽车保有量的平均增长率进行推测，2016-2018年的交通事故数分别为431起、334起、832起.表明罗长高速隧道群交通事故依然保持高发态势，特别是在2018年将达到峰值，应引起足够重视，采取相应预控措施.

[1] 中华人民共和国交通运输部.2015年交通运输行业发展统计公报[EB/OL].(2016-05-06)[2016-09-28].http://zizhan.mot.gov.cn/zfxxgk/bnssj/zhghs/201605/t20160506_2024006.html.

[2] 詹伟.山区高速公路长大隧道群区域交通安全保障技术研究[D].杭州：浙江大学，2013.

[3] 杨健，阳富强，沈斐敏.基于改进DSmT理论的公路隧道行车安全综合评价方法研究[J].中国安全科学学报，2016，26(8):116-121.

[4] 陈玉祥，张汉亚.预测技术与应用[M].北京:机械工业出版社，1985.

[5] SMEED R J.The usefulness of formulate in traffic engineering and road safety[J].Accident Analysis and Prevention，1972，4(4):303-312.

[6] MINTER A L.Road casualties-improvement by learning processes[J].Traffic and Control，1987(2):74-79.

[7] NAVIN F，BERGAN A，ZHANG G.Road safety model:some fundamental ideas in transportation research record [J].Transportation Research Record Journal of the Transportation Research Board，1996，1 563(1):48-57.

[8] OPPE S.Development of traffic and traffic safety:global trends and incidental fluctuations [J].Accident Analysis and Prevention，1991，23(5):413-422.

[9] 王孟莲，梁树甜，牛璐.最优组合预测方法在船舶电推系统中的应用[J].电机与控制学报，2015，19(9):103-107.

[10] 易富君.公路隧道群事故预防管理核心理论研究[D].南京:东南大学，2012.

[11] BATES J M，GRANGER C W J，The combination of forecasts[J].Journal of the Operational Research Society，1969，20 (4):451-468.

[12] 葛志鹏，李锐，张健，等.基于时间序列与GSVMR模型的短时交通量组合预测[J].长安大学学报(自然科学版)，2015，35(增刊1):222-226.

[13] 钟连德.高速公路事故预测模型研究[D].北京:北京工业大学，2008.

[14] 福建省统计局.年度数据[EB/OL].(2016-08-30)[2016-09-30].http://www.stats-fj.gov.cn/xxgk/ndsj/.

[15] 邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社，1996.

[16] FREEDMAN D.Markov Chains[M].New York:Spring，1983.

[17] 李相勇.道路交通事故预测方法研究[D].成都：西南交通大学，2004.

[18] 聂小沅，李德建.基于BP神经网络与GM(1，1)模型组合算法的桥梁耐久性预测[J].铁道科学与工程学报，2015，12(4):839-844.

(责任编辑：蒋培玉)

Study on nonlinear integrated forecasting method of traffic accidents in highway tunnel group

YANG Jian1,2，YANG Fuqiang2，SHEN Feimin2

(1.College of Civil Engineering，Fuzhou University，Fuzhou，Fujian 350116，China；2.College of Environments and Resources，Fuzhou University，Fuzhou，Fujian 350116，China)

In order to forecast the traffic accidents of tunnel group in Luoyuan-Changle section of Shenyang-Hainan highway.Considering the characteristics of nonlinear and dynamic of the traffic system in tunnel group,the method of nonlinear integrated forecasting based on BP neural network was studied,and the relative traffic accident frequency was regarded as forecast target.The results show that nonlinear integrated forecasting model can integrate effective implicit information from single forecast model such as exponent smooth model,nonlinear regression model and Grey Markov model.The accuracy of forecast is improved by this method,and a new way is pointed out for optimize the traffic accident prediction technology.By this method,with the increase of traffic volume,the traffic accident frequency in this tunnel group will first decreased and then increased sharply in the next 3 years(2016-2018).

tunnel group; relative traffic accident frequency; nonlinear forecasting; integrated forecasting method

10.7631/issn.1000-2243.2017.02.0226

1000-2243(2017)02-0226-05

2016-11-04

沈斐敏(1951-)，教授，主要从事事故预测与预防、安全系统工程的研究，feimshen@sina.com

国家自然科学基金资助项目(5130405)；福建省交通运输科技项目(201526)；福建省教育厅科技项目(JAT160090)

X951

A