一种压缩感知词典快速构造方法
张 业,李 佳
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
一种压缩感知词典快速构造方法
张 业,李 佳
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
提出一种基于交互投影方法的量测词典和感知词典构造算法。将量测词典和感知词典的类Gram矩阵向理想Gram矩阵集合投影并得到投影矩阵,再将此矩阵向类Gram矩阵集合投影,此过程如此继续直至满足终止条件,可得到一对弱相关量测和感知词典,其类Gram矩阵非主对角线元素接近或者达到Welch界。该算法采用一种新的向类Gram矩阵投影方法,可以极大地降低计算量,此算法得到的词典可有效提高OMP算法性能。
压缩感知;量测词典;感知词典;贪婪算法
0 引言
压缩感知理论是最近几年信号处理领域新发展起来的热点研究方向。如果信号是稀疏信号,压缩感知理论可以通过其非自适应线性投影精确恢复原信号。压缩感知减小了稀疏信号的量测量并在诸多领域得到广泛的研究[1-3]。
压缩感知理论主要涉及2个问题,一个是信号量测,另一个是信号恢复。对于信号量测,已有诸多类型量测词典相继被提出,比如部分傅里叶矩阵[4]、二值随机矩阵[5]以及确定性测量矩阵[6]等。信号恢复问题已有多种算法提出,比如基于贪婪算法的OMP算法、线性规划算法等。
实质上,信号的恢复与词典的“优劣”密切相关。通常用相关系数或者RIP(Restricted Isometry Property)[7-8]常数的大小来描述词典“优劣”,相关系数小的词典或者RIP常数小的词典可以有效提高信号恢复算法性能。因此,相关系数或RIP常数已成为诸多词典构造算法的标准。
文献[9]提出了感知词典的概念并给出了感知词典的构造方法,此方法降低了交叉相关系数,可以提高OMP和Thresholding算法性能。文献[10-11]提出了量测词典和感知词典构造方法,其交叉相关系数进一步减小,但解决线性约束最小二乘问题增加了计算量和复杂度。文献[12]给出了基于交互投影方法的等角紧支框架构造算法,对于部分维数矩阵其相关系数可达到Welch界,但对于大部分维数矩阵无法得到小相关系数矩阵。
1 压缩感知基本理论
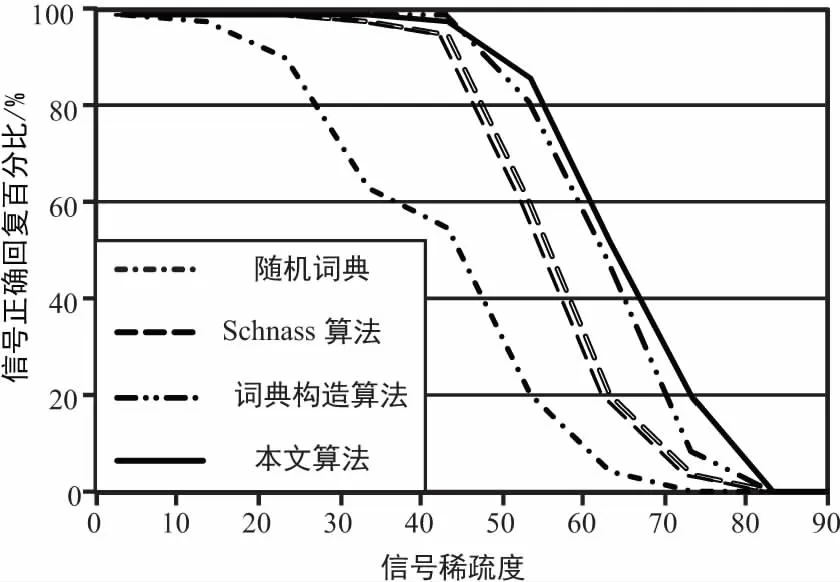
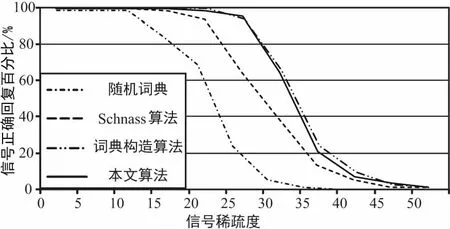
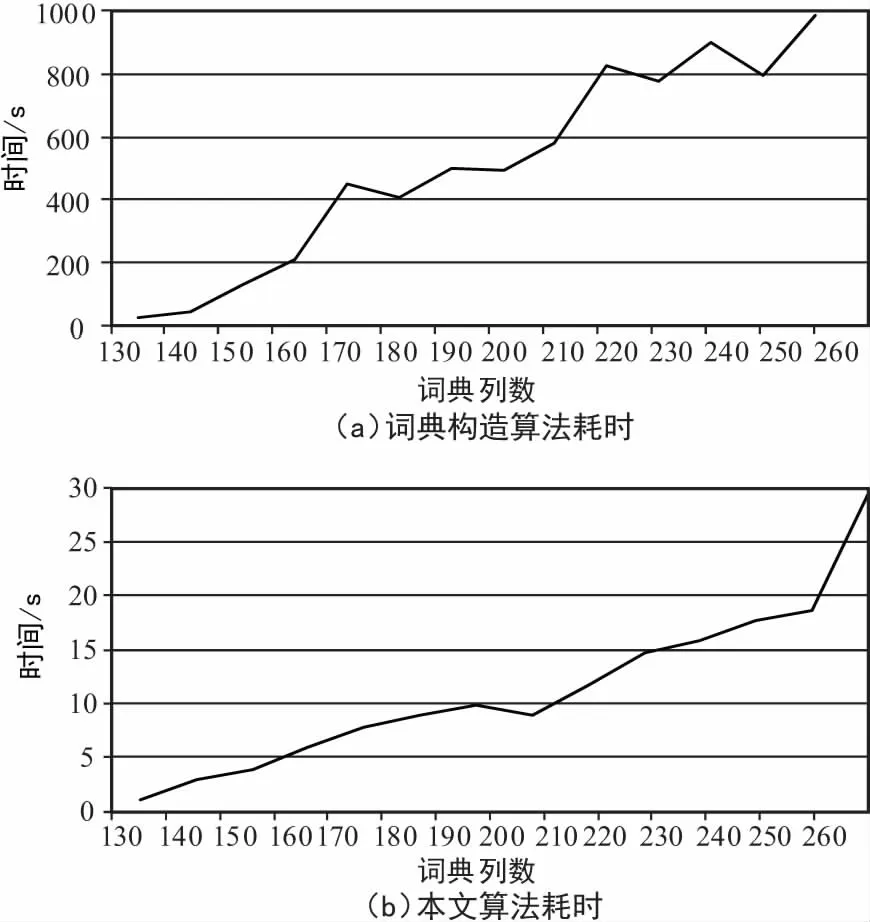
信号x∈Rn×1为k稀疏信号,即sup(x)≤k,sup(x)表示x中非零元素个数。Φ∈Rm×n为量测词典且m< min||x||0s.t.y=Φx, (1) l0最小问题是一个数学上的NP难题,因此直接求解此问题不现实。在量测矩阵满足一定条件下,l0最小问题与l1最小问题等价[6-7]。此后,基于l1最小问题求解算法不断涌现。 贪婪算法为解l0最小问题次优算法,尽管其性能不及基于求解l1最小问题的线性规划算法,但由于其计算量小而得到广泛应用。无论是l1与l0最小问题等价,还是各种恢复算法性能,都与量测词典性质相关,相关系数常用来衡量量测词典优劣。 定义1:对于单位化量测词典Φ∈Rm×n,相关系数和积累相关系数定义为: (2) (3) 式中,φi和φj分别为词典Φ的第i列和第j列。 文献[13]指出,当μ<2k-1或者μ1(k-1) +μ1(k)<1时,l0最小化问题与l1最小化问题解相同,且基追踪与OMP算法均可精确恢复稀疏信号。然而,由于量测词典是冗余词典(行数大于列数),其相关系数不可能为零,文献[13]指出,对于冗余实词典,当n≤m(m-1)/2时,其相关系数存在下限为: (4) 此下限被称为Welch界。满足相关系数达到Welch界矩阵成为Grassmannian框架[14]。 文献[9]提出感知词典概念,对于量测词典Φ∈Rm×n,存在感知词典Ψ∈Rm×n,使得 〈ψi,φi〉>>〈ψi,φj〉,对于1≤i,j≤n,i≠j, (5) 式中,ψi和ψj分别为词典Ψ的第i列和第j列。文献[6]同时提出了交叉相关系数感念。 定义2:对于量测词典Φ∈Rm×n和感知词典Ψ∈Rm×n,如果〈ψi,φi〉=1,1≤i≤n,则交叉相关系数和交叉积累相关系数定义为: (6) (7) 本文利用交互投影方法构造量测词典与感知词典。首先,定义类Gram矩阵集合G和理想Gram矩阵集合H如下[10]: G={G=ΨTΦ、Φ,Ψ∈Rm×n,1≤i≤n}, (8) (9) 式中,类Gram矩阵集合实质上为秩为m的矩阵集合,理想Gram矩阵集合为对角线元素绝对值为1,非对角线元素绝对值小于或等于Welch界矩阵集合。如果使量测词典与感知词典类Gram矩阵接近或成为理想Gram矩阵集合中的某一个矩阵,那么这对词典交叉相关系数将接近或者达到Welch界。本文提出的词典构造算法旨在解决此问题,给定初始量测和感知词典Φ和Ψ,类Gram矩阵为G=ΨTΦ,词典构造算法基本方法如下: ①H= ‖H′-G‖F,s.t.H′∈H; ②G= ‖G′-H‖F,s.t.G′∈G。 上述过程一直循环至终止条件满足。 下面解决上述方法涉及问题。对于步骤①问题,文献[12]给出如下结论: 定理3:对于给定的矩阵G,在集合H中存在矩阵H,其元素hij与矩阵G元素gij满足关系: (10) 则其Frobenius距离与矩阵G距离最短。 对于第2个问题,即如何在类Gram矩阵集合中寻找一矩阵使其与给定矩阵Frobenius距离最短,有以下结论。 定理4:对于给定矩阵H,对H进行奇异值分解,即H=SVD,其中矩阵V为一对角矩阵且对角线元素(即矩阵H奇异值或特征值)按非增顺序依次排列,令G=SVmD,其中Vm为一对角矩阵,前m个对角线元素为与V前m个对角线元素相同,其余对角线元素均为0。则矩阵G为集合G中与矩阵H的Frobenius距离最短矩阵。 证明:对于矩阵H和矩阵G′,令λ(H)与λ(G′)为矩阵H和矩阵G′特征值所构成的向量,且特征值按非增顺序排列。根据Wielandt-Hoffman定理[16]有: (11) 上述等式成立当且仅当矩阵G′和矩阵H特征向量相等。如果矩阵H有如下分解: H=SVD, (12) G′=SVmD, (13) 式中,Vm为一对角矩阵,前m个对角线元素为与V前m个对角线元素相同,其余对角线元素均为0。证毕。 基于上述讨论,本文所提出的感知词典与量测词典构造算法如下: 输入:高斯随机单位化矩阵Φ;程序退出条件e.初始化:G=ΦTΦ.循环:第i(i≥1)个循环①H=‖H′-G‖F,s.t.H′∈H;②H=UΛV,Λ=diag(λ(H));③G=UΛmV,ri=‖H-G‖F;④Λm=QTQ,Ψ=QUT,Φ=QV;⑤φi=φi/‖φi‖2,ψi=ψi/〈φi,ψi〉,1≤i≤n;⑥如果i≥2且ri-ri-1≤ε,退出;否则回到步骤①,i=i+1. 输出:感知词典Ψ和量测词典Φ. 算法步骤⑤中,对于得到的感知词典Ψ和量测词典Φ按照以下步骤处理: (14) 利用计算机仿真分析比较Schnass算法[9]、词典构造算法[10-11]与本文算法。算法仿真中,高斯随机矩阵作为初始化词典,算法终止条件常数为ε=10-5,每一实验重复500次。 图1给出了词典行数为128时,构造不同列数词典的交叉相关系数比较。可以看出,在交叉相关系数方面,词典构造算法和本文算法都优于Schnass的算法,同时本文算法略优于词典构造算法。 图1 各种词典列数所得到的交叉相关系数 图2和图3给出应用3种算法构造出的词典OMP性能比较,量测词典和感知词典的大小选为128×256。由图2可以看出,当稀疏信号非零成分幅度符合均值为0、方差为1的高斯分布时,即高斯稀疏信号,OMP算法利用本文算法构造出的词典,能得到略高于其他词典的重建性能。图3显示,当稀疏信号非零成分幅度为1时,即0-1稀疏信号,利用本文算法构造的词典和词典算法构造的词典OMP算法性能差不多。图2和图3同时表明,利用本文算法和词典构造算法构造的词典OMP性能都优于利用Schnass算法构造的词典和高斯随机词典。 图2 OMP算法重建高斯稀疏信号性能比较 图3 OMP算法重建0-1稀疏信号性能比较 选择行数为128,图4比较了构造不同列数词典时,词典构造算法和本文算法消耗时间。2种算法都应用于Matlab7.10.0.软件,WindowsXP系统,计算机配置为双核2.6GHzCUP,1.96G内存。从图4可以看出,本文算法耗时要远低于词典构造算法,大约仅为后者的1/30。 图4 构造不同列数词典算法耗时 词典构造算法由于通过文献[17-18]中方法解决大量的非线性优化问题而增加了计算量,相比之下本文算法在保持了词典构造算法的性能同时,降低了计算量。 利用交互投影算法,本文提出一种构造感知词典和量测词典方法,所构造的词典具有小的交叉相关系数而且可以改进OMP算法性能。相比于词典构造算法,本文的算法在保持了其优秀性能的同时,降低了计算量,在效率方面提高了约30倍。 [1]DonohoDL.CompressedSensing[J].IEEETrans.Inf.Theory,2006,52(4):1289-1306. [2] 石光明,刘丹华,高大华,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081. [3]CandesEJ.AnIntroductiontoCompressiveSampling:ASensing/samplingParadigmThatGoesAgainsttheCommonKnowledgeinDataAcquisition[J].IEEESignalProcess.Maga,2008,25(2):21-30. [4]GilbertAC,GubaS.NearOptimalSparseFourierRepresentationsviaSampling[C]∥InProceedingsofthe34thAnnualACMSymposiumonTheoryofComputing.Quebec,Canada,2006:152-161. [5]CandesEJ,TaoT.NearOptimalSignalRecoveryfromRandomProjections:UniversalEncodingStrategies[J].IEEETrans.Inf.Theory,2006,52(6):5406-5425. [6] 王 强,李 佳,沈 毅.压缩感知中确定性测量矩阵构造算法综述[J].电子学报,2013,41(10):2014-2050. [7]CandesEJ,TaoT.DecodingbyLinearProgramming[J].IEEETrans.Inf.Theory,2005,51(12):4203-4215. [8]CandesEJ.TheRestrictedIsometryPropertyandItsImplicationsforCompressedSensing[J].C.R.Acad.Sci.Pairs,2008,346(9-10):589-592. [9]SchnassK,VandergheynstP.DictionaryPreconditionforGreedyAlgorithms[J].IEEETrans.SignalProcess,2008,56(5):1994-2002. [10]LiB,ShenY,LiJ.DictionariesConstructionUsingAlternatingProjectionMethodinCompressiveSensing[J].IEEESignalProcessLett,2011,18(11):663-666. [11]李 佳,王 强,沈 毅,等.压缩感知中测量矩阵与重建算法的协同构造[J].电子学报,2013,41(1):29-34. [12]TroppJA.DesigningStructuredTightFramesviaanAlternatingProjectionMethod[J].IEEETrans.Inf.Theory,2005,51(1):188-209. [13]TroppJA.GreedIsGood:AlgorithmicResultsforSparseApproximation[J].IEEETrans.Inf.Theory,2004,50(10):2231-2242. [14]WelchLR.LowerBoundontheMaximumCrossCorrelationofSignals[J].IEEETrans.Inf.Theory,1974,IT-20(3):397-399. [15]StrohmerT,HeathRW.GrassmanianFrameswithApplicationstoCodingandCommunication[J].Appl.Comput.Harmon.Anal,2003,14(3):257-275. [16]HornRA,JohnsonCR.MatrixAnalysis[M].Cambridge:CambridgeUniversityPress,1985. [17]GillPE,MurrayW,WrightMH.PracticalOptimization[M].UK:AcademicPress,1981. [18]ColemanTF,LiY.AReflectiveNewtonMethodforMinimizingaQuadraticFunctionSubjecttoBoundsonSomeoftheVariables[J].SIAMJ.Optim,1996,6(4):1040-1058. A Fast Dictionary Construction Algorithm in Compressive Sensing ZHANG Ye,LI Jia (The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China) This paper presents a measurement and sensing dictionary construction algorithm in compressive sensing based on the alternating projection method.Gram-like matrix of measurement and sensing dictionaries is projected on the set of ideal Gram matrix,then the obtained matrix is projected on the set of Gram-like matrix.This procedure is repeated until the termination condition is met and a pair of measurement and sensing dictionaries will be obtained.The off diagonal entries of the Gram-like matrix reach or approach the Welch bound.The algorithm in this paper involves a novel method to project a matrix on the set of Gram-like matrix,which can reduce the computation amount.This algorithm improves the performance of greedy algorithm such as OMP. compressive sensing;measurement dictionary;sensing dictionary;greedy algorithm 10.3969/j.issn.1003-3114.2017.03.07 张 业,李 佳.一种压缩感知词典快速构造方法[J].无线电通信技术,2017,43(3):30-33. [ZHANG Ye,LI Jia.A Fast Dictionary Construction Algorithm in Compressive Sensing [J].Radio Communications Technology,2017,43(3):30-33.] 2017-01-19 河北省重大科技成果转化专项项目(14040322Z) 张 业(1984—),男,工程师,主要研究方向:数字信号处理、计算机网络及信息系统。李 佳(1986—),男,工程师,主要研究方向:数字信号处理、认知无线电、稀疏优化算法。 TN911 A 1003-3114(2017)03-30-4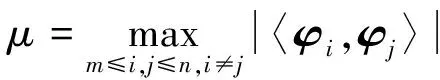



2 量测与感知词典构造方法





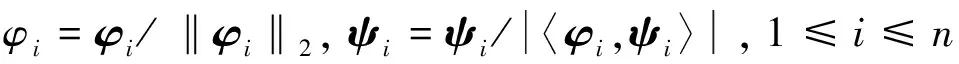
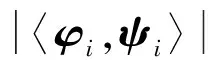
3 仿真分析

4 结束语

