藏北地区土壤水分遥感反演模型的研究①

拉 巴，卓 嘎，陈 涛

(1 中国气象局成都高原气象研究所拉萨分部，拉萨 850001；2 西藏高原大气环境科学研究所，拉萨 850001；3 西藏自治区气候中心，拉萨 850001)

藏北地区土壤水分遥感反演模型的研究①

拉 巴1,2，卓 嘎3，陈 涛1

(1 中国气象局成都高原气象研究所拉萨分部，拉萨 850001；2 西藏高原大气环境科学研究所，拉萨 850001；3 西藏自治区气候中心，拉萨 850001)

土壤水分是反映地表土壤特性的重要表征参量，也是遥感反演领域的一个热点问题。利用MODIS卫星数据第7波段对水分变化较敏感的特点，构建了一种简单实用的土壤水分反演回归模型。结果表明，利用该模型计算的预测值与实地观测值间的相关性比较好，达到了显著水平(P<0.001)，可以作为研究区土壤含水量遥感反演回归模型。由于该方法具有简单实用的特点，为高原土壤水分遥感监测提供了可行的方法。

土壤水分；MODIS；反射率；模型

土壤水分是表示土壤退化或干旱的重要表征参量，也是气候、水文、生态、农业等领域衡量干旱程度的重要指标，是影响全球气候和环境变化的重要因素。因此，了解土壤水分状况在土地规划和管理及农牧业生产中具有十分重要的现实意义。大范围的土壤水分监测是农业过程研究和环境因子评价的重要组成部分，而区域尺度甚至全球范围的土壤水环境反演又是陆地过程模式研究中必不可少的一个参量，传统的土壤水分监测方法大多是野外实地观测，其中最准确的属质量法，能得出精确的土壤水分的质量百分比[1]，但是消耗大量的时间和人力。还有利用土壤水分不同其相应的导电性能也不同的特点发展起来的嵌入式传感器测量法[2]，能够节省大量的时间和劳动力，但是仍然是实验点上的监测而不能推广到大范围的面上。以上这些传统的监测手段都具有相同的缺点，既费时、费力，又可测点少，代表性差，从而导致时间分辨率低，无法实现大面积、大范围土壤水分的实时动态监测。

随着遥感技术的不断发展，在20世纪80年代遥感监测土壤水分克服了传统方法的缺陷，使大范围区域土壤水分监测成为可以实现的目标。首先，在国外有利用可见光和红外遥感监测土壤水分的研究，如Jackson等[3]利用NDVI监测干旱指数、Kogan[4]提出的植被状态指数(VCI)、Bijleveld[5]建立的计算热惯量和每日蒸发量模型以及 Pratt和 Ellyett[6]提出绘制土壤水分和地理图的热惯量方法等。到20世纪90年代中后期，随着NOAA/AVHRR和MODIS数据的普遍应用，光学和热红外波段的遥感反演也逐渐成熟。有很多学者[7–9]研究了不同空间和时间及光谱分辨率的卫星数据(AVHRR、TM、SPOT等)下Ts(地表温度)、NDVI斜率与土壤湿度的关系。在国内，土壤水分遥感反演方面的研究也比较早，有关研究论文也不少，如 20世纪 80年代中期，朱永豪等[10]研究了不同湿度条件下土壤光谱反射率的关系。20世纪90年代以后，土壤水分遥感反演理论和应用得到迅速发展，土壤水分遥感反演新方法、新模型不断出现[11–19]。赵杰鹏等[20]利用温度植被干旱指数(TVDI)法对新疆地区土壤水分进行反演，指出消除云层影响后，TVDI模型能更好地适用于大范围土壤水分的遥感估算。另外也有部分研究指出位于短波红外波段的MODIS第6波段和第 7波段对水分变化较敏感[21–22]，以此构建的土壤湿度指数也可以用于土壤水分的估算，也有仅用第7波段做的分析，发现该波段与土壤水分间也有较好的线性相关性[23]。

综上所述，土壤湿度的遥感反演技术已基本成熟并得到了广泛实用，但考虑到高原地区海拔高、土壤湿度观测站点几乎没有、下垫面条件复杂多变等原因，把内地平原和地形条件相对单一地区展开的实验结果直接用于高原上对反演结果造成更大的误差。因此本文以已有的研究结论和方法为基础和参考，利用实测数据与卫星数据相结合的方式，继续探究MODIS第7波段与土壤水分的关系在高原地区的变化，最终找出一种利用单波段反演土壤水分的简便实用模型，将该模型应用于日常的遥感监测服务中，为遥感业务工作人员节省时间，提高工作效率。

1 材料与方法

1.1 数据及研究区概况

MODIS数据(Moderate Resolution Imaging Spectroradiometer)是由美国在1999年12月发射成功，并且该数据向全球免费播放。MODIS具有 36个波段(0.405 ~ 14.385 µm波长)，拥有250、500、1 000 m的3个不同的空间分辨率，扫描宽度2 330 km，只需2 ~ 3轨即可覆盖全国[21]。从水的吸收率曲线(图 1)可以看到，水体在1.4、2.0 µm波长附近存在有很高的吸收峰，如果土壤中水体含量较多，则在这些波长上土壤反射率应该是低值，反之为高值。本文选取MOD09GA.005地表反射率数据集中第7波段(2.105 ~ 2.135 µm)的地表反射率数据来计算含水率，数据可以直接从 NASA网站上获取，已经过地理定标和大气矫正处理，空间分辨率为500 m。

图1 水的吸收率曲线[23]Fig. 1 Water absorption rate curve

土壤水分观测仪器为ECH2O土壤含水量监测系统，每台仪器有5个探头，分别埋深于2、5、10、20、30 cm，共5个不同深度。数据采样时间间隔为10 min。该系统是美国Decagon公司研制的土壤水分传感器，通过测量土壤的介电常数来计算土壤体积含水量，通过测量传感器上电容的变化，从而测量插入介质的介电常数或电容率。由于水的介电常数非常高，因此当土壤中的水分含量变化时，土壤的介电常数也随之发生相当大的变化。ECH2O传感器电路可以把温度变化对测定的影响减小到最低。仪器最高灵敏度能达到0.1%，所测土壤湿度的精度最高能达到3% 以内。

观测样区选择在以那曲地区那曲县和聂荣县境内的典型高寒草原区域(图 2)，各观测点平均海拔在4 600 m以上，植被以小蒿草草甸为主。样区选择在50 km×50 km范围内，选取了8个观测点，相邻样点之间直线标准距离25 km，呈田字状排列，且要求地表类型单一，无湖泊或湖泊很少，草地植被覆盖在60% 以上，以确保观测样区无混合像元的影响。并要求草地类型单一、地势平坦、交通方便，利于人工看护仪器设备和定期数据导出与备份。本文中由于观测站点 a和erm的数据测量仪器与其余各点间不统一，未选取这两点的数值。

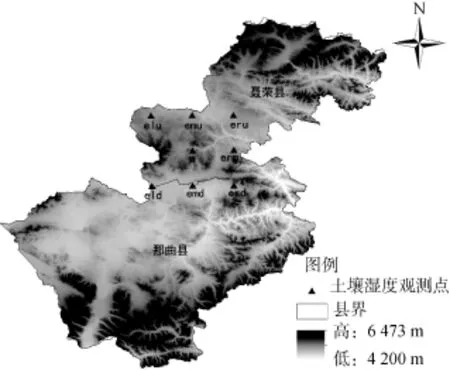
图2 研究区各观测点分布Fig. 2 Study area and observation point distribution

1.2 数据处理

由于研究区的 6个实地观测点位于数据编号为h25v05的范围内，只需下载编号为 h25v05的 2014年9月至2015年7月卫星过境观测点晴空时段所有数据，不需要拼接处理。该数据集中包括通道1 ~ 7的反射率值，首先，在MRT软件中对数据进行预处理，包括重采样和重投影，各参数设置如下：提取波段数据选第7波段的反射率，数据空间分辨率为500 m，投影方式统一为 Geographic投影，数据格式用Geotiff，重采样方法为Nearest Neighbor，对获取的数据乘0.000 1，得到第7波段反射率值。野外实测数据的时间分辨率为10 min，数据采集时段与卫星数据保持一致，数据处理过程如下：首先，查询MODIS数据卫星轨道过境和出境时段，将此时段作为实测数据提取的时间；其次，以卫星过境前后10 min的土壤观测数据作为地面验证数据，由于卫星观测所得数据为地球表面地物的反射率，因此选取6个观测点深度为2 cm土壤水分数据作为地面验证数据，将数据取算术平均代表该点的土壤水分观测值，土壤湿度数据统计分析处理(包括回归模型建立和图形绘制)均在R软件中完成，卫星资料分析制图在ArcGIS中完成。

2 模型构建

在分析MODIS第7波段地表反射率数据和野外观测土壤水分数据关系(图 3)发现，7个观测点值基本上都在拟合直线附近波动，从而可以认为二者基本上呈线性负相关，而这些点与直线的偏离是由其他一切不确定因素影响造成的，根据第7波段与土壤含水量存在的线性相关性，可以假定Y = β0+ β1X + ε，为线性模型方程，其中，β0+ β1X表示土壤水分Y随第7波段地表反射率而变化的部分；ε是随机误差，是其他一切不确定因素影响总和，其值是不可观测的。在这里假定ε ~ N(0，σ2)，求出线性回归方程中各参数 β0、β1的最小二乘估计值及对方程作显著性水平检验发现，在给定显著性水平(α = 0.05)下，回归方程均通过了回归参数和回归方程的检验，残差的标准差也很小，非常显著，但绝对系数 R2较小(<0.55)，说明所得的回归方程并非为最优回归方程，需要再次考虑对回归方程的改进和进一步优化。

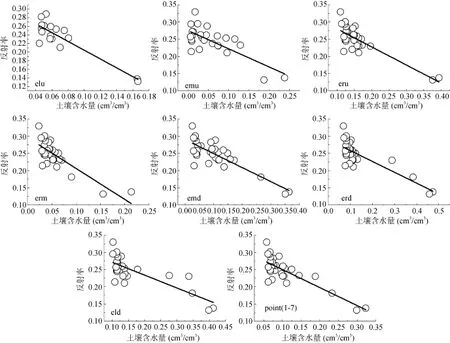
图3 MODIS第7波段反射率与土壤体积含水量散点图Fig. 3 Scatter diagrams of MODIS band 7 reflectance and soil volumetric water content

再进一步详细考虑各观测点实验数值与卫星数据之间的关系，若考虑曲线拟合可以发现所有观测点的要素绝对系数R2均会有显著提高，表明两者的关系不仅仅用简单的线性方程加以确定，需要建立变量和自变量间新的回归方程进行分析，并且在新的方程中把曲线拟合的关系加以考虑。在经过反复的试验分析后，最终可以将反映两者关系的回归方程假设为 Y = β0+ β1X +β2X2+ε形式，其中，β0+ β1X+β2X2表示土壤水分Y随第7波段地表反射率的变化而变化的部分，在原有的线性模型基础上，考虑了反射率与土壤水分的二次曲线拟合关系。ε同样是随机误差，为一切不确定因素影响的总和，其值是不可观测的。在这里假定ε ~ N (0，σ2)，可以作为反演模型使用，并对回归方程的参数和方程进行检验。结果表明，与原模型相比(表1)，该模型的绝对系数R2得到显著提高，平均每个点提高了0.19，因此，考虑第7波段反射率与土壤水分间的曲线拟合关系是可行的。回归方程的残差标准差也得到了更好的控制，回归方程的各参数、方程、残差标准差、绝对系数均非常显著，并在给定的显著性水平下，都分别通过了T和P检验。对所有样本观测点的数据建立回归方程，得到可以用来反演土壤水分的最终模型回归方程，回归方程参数能通过(P<0.001)检验，绝对系数为0.62，也通过了显著性水平检验，因此，回归方程可以作为藏北地区大范围土壤水分反演模型。

表1 各观测点土壤水分反演回归方程及绝对系数、显著性检验结果Table 1 Soil moisture inversion regression equation, correlation coefficient, significance test in each observation point

3 模型预测及验证分析

为了验证遥感估算模型的精度，利用 2015年 3月至7月底研究区晴空MODIS第7波段的反射率产品数据，对研究区土壤水分数据进行预测反演，从反演结果影像中提取对应的观测点像元的反演数值，与野外实地观测值对比分析可以看出(图 4)，反演值和实测数据的平均值之间具有非常高的线性相关性(绝对系数为 0.93)，对所有观测数据进行对比分析，两者间也有较好的相关性(相关系数为0.62)；地面观测和模型估算的两组数据平均值分别为 0.126 cm3/cm3和0.187 cm3/cm3，方差为0.008 6和0.003 5，相对误差为 1.5%，两组数据的大小和变化均差别较小，模型反演的结果总体上略大于实测值；对验证的所有数据进行分析，两者的均方根误差和平均相对误差分别为 7.03% 和 3.48%。模型产生的误差可能来源于研究区空间尺度上观测点较少，时间尺度上与卫星过境同步的晴空日数有限，因此在后续研究中，在条件允许下，可以适当增加观测密度及范围，对提高反演精度和效果有利。

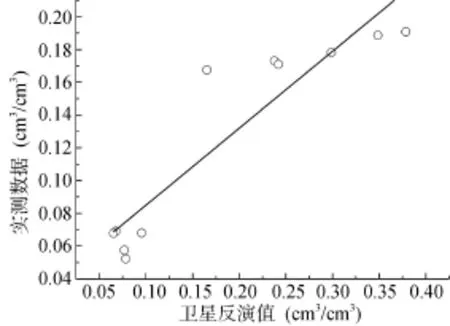
图4 实测土壤水分与模型估算结果间的比较Fig. 4 Comparison between measured and estimated soil moistures

使用新建立的回归模型，绘制了研究区土壤水分空间分布图(图5)。研究区7月份土壤水分显著大于 5月份，5月份土壤水分较高的区域主要分布在聂荣县北部和那曲县南部区域，部分地区土壤水分达到0.2 cm3/cm3以上的水平，其余大部分区域土壤水分值均小于 0.1 cm3/cm3，占研究区总面积的15.76%，研究区平均土壤水分为0.122 8 cm3/cm3，最大值为0.38 cm3/cm3，最小值为0.067 cm3/cm3；7月份土壤水分在0.1 ~ 0.2 cm3/cm3的区域主要集中在那曲县东部、聂荣县中部部分区域，面积占研究区总面积的12.78%，土壤水分值在0.1 cm3/cm3以下的区域主要分布在那曲县西部、聂荣县南部和北部部分区域。研究区7个观测点5月份土壤水分差距不大，均小于0.1 cm3/cm3，7月份观测点emu、eru和erd的土壤水分值均大于0.1 cm3/cm3，大于其余4个点。

4 结论

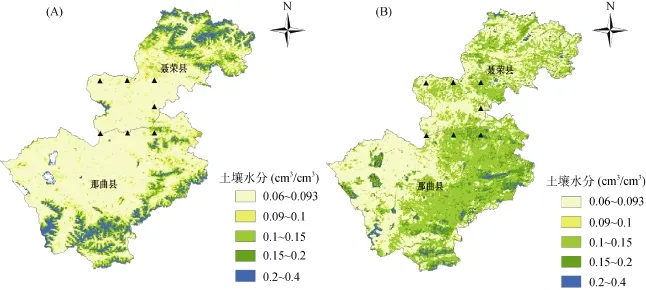
图5 藏北土壤水分反演(A. 2015年5月5日；B. 2015年7月24日)Fig. 5 Soil moisture inversion of northern Tibet (A. May 5, 2015; B. July 24, 2015)

本文将MODIS短波红外波段应用于土壤水分监测中，发现具有较好的应用效果。并基于MODIS第7波段的光谱特征与土壤水分之间的关系，构建了简单实用的MODIS土壤水分监测模型。与实测数据对比分析，结果显示二者具有较好的相关性，拟合方程通过了统计的显著性水平检验，表明该方法对土壤水分监测十分有效。模型简单易用，可用于日常遥感监测业务服务工作中，为中尺度的土壤水分监测提供了可靠的工具。因此，MODIS第7波段反射率可以作为藏北地区土壤水分反演的数据，用于大面积、多时相的干旱监测是可行的。

模型构建过程中，实测数据均位于藏北那曲高海拔、植被稀疏地区，因此该模型应用范围仅限于藏北地区或具有类似下垫面特征区域使用。鉴于青藏高原面积大，地表类型和气候特征复杂多变等原因，后续研究中建议在不同下垫面类型内均匀选择用于验证的土壤水分监测点，用于提高模型精度，优化模型。在海拔较低、湿度较大高原其他地区的第7波段反射率与土壤水分的关系也需要进一步的分析研究。

[1] Foody G M. Soil moisture content ground data for remote sensing investigation of agriculture region[J]. Int. J. Remote Sensing, 1991, 12(7): 1461–1469

[2] Cassel D K, Klute A. Water potential: Tensiometry // Klute A. Methods of soil analysis: Part 1-Physical and mineralogical methods[M]. Madison, WI: American Society of Agronomy, Soil Science Society of America, 1986

[3] Jackson R D, Slaler P N, Pinter P J. Discrimination of growth and water stress in wheat by various vegetation indices through clear and turbid atmosphere[J]. Remote Sensing of Environment, 1983, 13: 187–208

[4] Kogon F N. Remote sensing of weather impacts on vegetation in non-homogeneous areas[J]. Int. of Remote Sensing, 1990, 11: 1405–1420

[5] Bijleveld R A. ‘Tell Us’ a combined surface temperature, soil moisture and evaporation mapping approach[C]. Paper Presented at 12th Int. Symp. on Rem. Sens. of Env. Manila, Philippines, 1978: 20–25

[6] Pratt A, Ellyett C D. The thermal inertia approach to mapping of soil moisture and geology[J]. Remote Sensing of Environment, 1979, 8(2): 151–168

[7] Goetz S J. Multi-sensor analysis of NDVI, surface temperature and biophysical variables at a mixed grassland site[J]. International Journal of Remote Sensing, 1997, 18(1): 71–94

[8] Gillies R R, Carlson T N, Gui J, et al. Averification of the‘triangle’ method for obtaining surface soil water content and energy fluxes from remote measurements of the Normalized Difference Vegetation Index (NDVI) and surface radiant temperature[J]. International Journal of Remote Sensing, 1997, 18(15): 3145–3166

[9] Sandholt I, Rasmussen K, Andersen J. A simple interpretation of the surface temperature vegetation index space for assessment of surface moisture status[J]. Remote Sensing of Environment, 2002, 79(2/3): 213–224

[10] 朱永豪, 邓仁达, 卢亚非, 等. 不同湿度条件下黄棕壤光谱反射率的变化特征及其遥感意义[J]. 土壤学报, 1984, 21(2): 194–202

[11] 蒋金豹, 张玲, 崔希民, 等. 基于L波段的裸土区土壤水分微波遥感反演研究[J]. 土壤, 2014, 46(2): 361–365

[12] 焦俏, 王飞, 李锐, 等. ERS卫星反演数据在黄土高原近地表土壤水分中的应用[J]. 土壤学报, 2014, 51(6): 1338–1397

[13] 兰鑫宇, 郭子祺, 田野, 等. 土壤湿度遥感估算同化研究综述[J]. 地球科学进展, 2015, 30(6): 668–679

[14] 隋洪智, 田国良, 李付琴. 农田蒸散双层模型及其在干旱遥感监测中的应用[J]. 遥感学报, 1997, 1(3): 220–224

[15] 刘玉娇, 朱青, 吕立刚, 等. 基于时间稳定性和降维因子分析的土壤水分监测优化[J]. 土壤, 2016, 48(1):186–192

[16] 张仁华. 土壤含水量的热惯量模型及其应用[J]. 科学通报, 1991, 36(12): 924–927

[17] 田国良. 土壤水分的遥感监测方法[J]. 环境遥感, 1991, 6(2): 89–98

[18] 刘培君, 张琳, 艾里西尔.库尔班, 等. 卫星遥感估测土壤水分的一种方法[J]. 遥感学报, 1997, 1(2): 135–138

[19] 汪潇, 张增祥, 赵晓丽, 等. 遥感监测土壤水分研究综述[J]. 土壤学报, 2007, 44(1): 157–163

[20] 赵杰鹏, 张显峰, 廖春华, 等. 基于TVDI的大范围干旱区土壤水分遥感反演模型研究[J]. 遥感技术与应用, 2011, 26(6): 742–750

[21] 郭铌, 陈添宇, 雷建勤, 等. 用 NOAA 卫星可见光和红外资料估算甘肃省东部农田区土壤湿度[J]. 应用气象学报, 1997, 8(2): 212–218

[22] 姚云军, 秦其明, 赵少华, 等. 基于 MODIS短波红外光谱特征的土壤含水量反演[J]. 红外与毫米波学报, 2011, 30(1): 9–14

[23] 郭广猛, 赵冰茹. 使用MODIS数据监测土壤湿度[J]. 土壤, 2004, 36(2): 219–221

Remote Sensing Inversion Model of Soil Moisture of Northern Tibet Region

LA Ba1,2, ZHUO Ga3, CHEN Tao1
(1 Lhasa Branch of Chengdu Plateau Meteorological Research Institute of China, Lhasa 850001, China; 2 Tibet Institute of Plateau Atmospheric and Environmental Science, Lhasa 850001, China; 3 China Meteorological Administration, Lhasa 850001, China)

Soil moisture is an important parameter to reflect surface soil properties and also is a hot topic in remote sensing inversion field. A simple and practical soil moisture retrieval regression model was established based on the sensitivity of MODIS band 7 data to moisture changes. The results showed that the new model worked well in soil moisture inversion in the study area, and significant correlation was found between the field observed data and inversed data of soil moisture (P<0.001). The new model is simple, practical and feasible, and can be used to monitor soil moisture in northern Tibet and other plateau regions.

Soil moisture; MODIS; Reflectance; Model

P237

A

10.13758/j.cnki.tr.2017.01.025

中国气象局气候变化专项(CCSF201515)、国家自然科学基金项目(41165002，41465006)、中国气象局气象新技术推广项目(CMAGJ2013M51)和中国气象局成都高原气象研究所高原气象开放基金项目(LPM2012006)资助。

拉巴(1983—)，男，西藏拉萨人，硕士研究生，主要从事遥感应用研究。E-mail: xilaba@sohu.com